Положение (геометрия)

Вектор, представляющий положение точки относительно фиксированного начала координат.

Радиус-вектор представляет положение точки относительно начала координат O. В декартовой системе координат ${\displaystyle {\vec {r}}}$ ${\displaystyle \mathrm {P} (x,y,z)}$ ${\displaystyle {\vec {r}}=x\,{\hat {e}}_{x}+y\,{\hat {e}}_{y}+z\,{\hat {e}}_{z}.}$

В геометрии позиция или вектор позиции , также известный как вектор местоположения или радиус-вектор , является евклидовым вектором , который представляет точку P в пространстве . Его длина представляет расстояние относительно произвольного начала отсчета O , а его направление представляет угловую ориентацию относительно заданных осей отсчета. Обычно обозначается x , r , или s , он соответствует отрезку прямой линии от O до P . Другими словами, это смещение или перенос , который отображает начало координат в P : ^[1]

${\displaystyle \mathbf {r} ={\overrightarrow {OP}}.}$

Термин вектор положения используется в основном в областях дифференциальной геометрии , механики и иногда векторного исчисления . Часто это используется в двумерном или трехмерном пространстве , но может быть легко обобщено на евклидовы пространства и аффинные пространства любой размерности . ^[2]

Относительное положение

Относительное положение точки Q относительно точки P — это евклидов вектор, полученный в результате вычитания двух векторов абсолютного положения (каждого относительно начала координат):

${\displaystyle \Delta \mathbf {r} =\mathbf {s} -\mathbf {r} ={\overrightarrow {PQ}},}$

где . Относительное направление между двумя точками — это их относительное положение, нормализованное как единичный вектор ${\displaystyle \mathbf {s} ={\overrightarrow {OQ}}}$

Определение и представление

Три измерения

Пространственная кривая в 3D. Вектор положения r параметризуется скаляром t . При r = a красная линия является касательной к кривой, а синяя плоскость является нормалью к кривой.

В трех измерениях любой набор трехмерных координат и соответствующих им базисных векторов может быть использован для определения местоположения точки в пространстве — можно использовать тот, который проще для поставленной задачи.

Обычно используют знакомую декартову систему координат , а иногда сферические полярные координаты или цилиндрические координаты :

${\displaystyle {\begin{aligned}\mathbf {r} (t)&\equiv \mathbf {r} (x,y,z)\equiv x(t)\mathbf {\hat {e}} _{x}+y(t)\mathbf {\hat {e}} _{y}+z(t)\mathbf {\hat {e}} _{z}\\&\equiv \mathbf {r} (r,\theta ,\phi )\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\theta (t),\phi (t){\big )}\\&\equiv \mathbf {r} (r,\phi ,z)\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\phi (t){\big )}+z(t)\mathbf {\hat {e}} _{z},\\\end{aligned}}}$

где t — параметр , из-за их прямоугольной или круговой симметрии. Эти различные координаты и соответствующие базисные векторы представляют один и тот же вектор положения. Вместо этого можно использовать более общие криволинейные координаты , которые используются в таких контекстах, как механика сплошной среды и общая теория относительности (в последнем случае требуется дополнительная временная координата).

нразмеры

Линейная алгебра допускает абстракцию n -мерного вектора положения. Вектор положения может быть выражен как линейная комбинация базисных векторов: ^{[3] [4]}

${\displaystyle \mathbf {r} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}=x_{1}\mathbf {e} _{1}+x_{2}\mathbf {e} _{2}+\dotsb +x_{n}\mathbf {e} _{n}.}$

Набор всех векторов положения образует пространство положения ( векторное пространство , элементами которого являются векторы положения), поскольку положения могут быть сложены ( сложение векторов ) и масштабированы по длине ( скалярное умножение ) для получения другого вектора положения в пространстве. Понятие «пространство» интуитивно понятно, поскольку каждый x _i ( i = 1, 2, …, n ) может иметь любое значение, набор значений определяет точку в пространстве.

Размерность позиционного пространства равна n (также обозначается dim( R ) = n ). Координаты вектора r относительно базисных векторов e _i равны x _i . Вектор координат образует координатный вектор или n - кортеж ( x ₁ , x ₂ , …, x n ₎ .

Каждая координата x _i может быть параметризована рядом параметров t . Один параметр x _i ( t ) будет описывать искривленный 1D-путь, два параметра x _i ( t ₁ , t ₂ ) описывают искривленную 2D-поверхность, три x _i ( t ₁ , t ₂ , t ₃ ) описывают искривленный 3D-объем пространства и т. д.

Линейная область базисного набора B = { e ₁ , e ₂ , …, e _n } равна позиционному пространству R , обозначаемому как span( B ) = R .

Приложения

Дифференциальная геометрия

Поля векторов положения используются для описания непрерывных и дифференцируемых пространственных кривых, в этом случае независимым параметром не обязательно должно быть время, но может быть (например) длина дуги кривой.

Механика

В любом уравнении движения вектор положения r ( t ) обычно является наиболее востребованной величиной, поскольку эта функция определяет движение частицы (т.е. точечной массы ) – ее местоположение относительно заданной системы координат в некоторый момент времени t .

Чтобы определить движение в терминах положения, каждая координата может быть параметризована временем; поскольку каждое последующее значение времени соответствует последовательности последовательных пространственных положений, заданных координатами, пределом континуума многих последовательных положений является путь, проходимый частицей.

В случае одного измерения позиция имеет только один компонент, поэтому она фактически вырождается в скалярную координату. Это может быть, скажем, вектор в направлении x или радиальном направлении r . Эквивалентные обозначения включают

${\displaystyle \mathbf {x} \equiv x\equiv x(t),\quad r\equiv r(t),\quad s\equiv s(t).}$

Производные

Кинематические величины классической частицы: масса  m , положение  r , скорость  v , ускорение  a

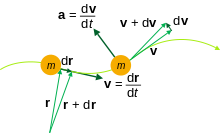
Для вектора положения r, который является функцией времени t , производные по времени могут быть вычислены относительно t . Эти производные имеют общую полезность при изучении кинематики , теории управления , инженерии и других наук.

Скорость

${\displaystyle \mathbf {v} ={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}},}$

где d r — бесконечно малое смещение (вектор) .

Ускорение

${\displaystyle \mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}.}$

Придурок

${\displaystyle \mathbf {j} ={\frac {\mathrm {d} \mathbf {a} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} }{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} }{\mathrm {d} t^{3}}}.}$

Эти названия для первой, второй и третьей производной положения обычно используются в базовой кинематике. ^[5] В более широком смысле производные более высокого порядка могут быть вычислены аналогичным образом. Изучение этих производных более высокого порядка может улучшить приближения исходной функции смещения. Такие члены более высокого порядка требуются для точного представления функции смещения как суммы бесконечной последовательности , что позволяет использовать несколько аналитических методов в инженерии и физике.

Смотрите также

• Аффинное пространство
• Система координат
• Горизонтальное положение
• Элемент линии
• Параметрическая поверхность
• Фиксация положения
• Позиция четырехвекторная
• Шесть степеней свободы
• Вертикальное положение

Примечания

1. Термин «перемещение» в основном используется в механике, тогда как «перенос» — в геометрии.
2. Келлер, Ф.Дж., Геттис, У.Э. и др. (1993), стр. 28–29.
3. Райли, К. Ф.; Хобсон, М. П.; Бенс, С. Дж. (2010). Математические методы для физики и техники . Cambridge University Press. ISBN 978-0-521-86153-3.
4. Липшуц, С.; Липсон, М. (2009). Линейная алгебра . МакГроу Хилл. ISBN 978-0-07-154352-1.
5. Стюарт, Джеймс (2001). "§2.8. Производная как функция". Исчисление (2-е изд.). Брукс/Коул. ISBN 0-534-37718-1.

Ссылки

• Келлер, Ф. Дж., Геттис, У. Э. и др. (1993). «Физика: классическая и современная», 2-е изд. McGraw Hill Publishing.

Внешние ссылки

• Медиа, связанные с Позицией (геометрия) на Wikimedia Commons