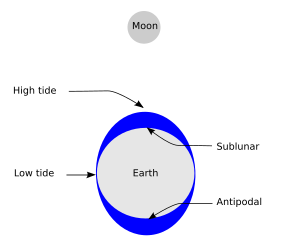
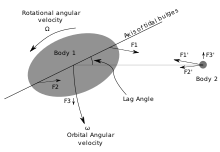

Приливы — это подъем и падение уровня моря , вызванные совокупным воздействием гравитационных сил , оказываемых Луной (и в гораздо меньшей степени Солнцем ), а также вращением Земли и Луны друг вокруг друга.
Таблицы приливов можно использовать для любого местоположения, чтобы найти прогнозируемое время и амплитуду (или « приливной диапазон »). Прогнозы зависят от многих факторов, включая выравнивание Солнца и Луны, фазу и амплитуду прилива (модель приливов в глубоком океане), амфидромные системы океанов, а также форму береговой линии и прибрежной батиметрии (см. Расчет времени ). Однако это всего лишь прогнозы, фактическое время и высота прилива зависят от ветра и атмосферного давления . Многие береговые линии испытывают полусуточные приливы — два почти равных прилива и отлива каждый день. В других местах прилив суточный — один прилив и один отлив каждый день. «Смешанный прилив» — два прилива неравной величины в день — это третья регулярная категория. [1] [2] [a]
Приливы варьируются в масштабах времени от нескольких часов до нескольких лет из-за ряда факторов, которые определяют лунный интервал . Для точных записей мареографы на стационарных станциях измеряют уровень воды с течением времени. Манометры игнорируют изменения, вызванные волнами с периодами короче минут. Эти данные сравниваются с опорным (или базовым) уровнем, обычно называемым средним уровнем моря . [3]
Хотя приливы обычно являются крупнейшим источником краткосрочных колебаний уровня моря, уровень моря также подвержен изменениям из-за теплового расширения , ветра и изменений барометрического давления, что приводит к штормовым нагонам , особенно в мелководных морях и вблизи побережий.
Приливные явления не ограничиваются океанами, но могут происходить и в других системах, где присутствует гравитационное поле, которое меняется во времени и пространстве. Например, форма твердой части Земли слегка подвержена влиянию земного прилива , хотя это не так легко заметить, как приливные движения воды.
В приливном цикле выделяют четыре этапа:
Осциллирующие течения, создаваемые приливами, известны как приливные течения или приливные течения . Момент, когда приливное течение прекращается, называется слабой водой или слабым приливом . Затем прилив меняет направление и говорят, что он поворачивает. Слабая вода обычно возникает вблизи высокой и низкой воды, но есть места, где моменты слабой воды значительно отличаются от моментов высокой и низкой воды. [4]
Приливы обычно бывают полусуточными (два прилива и два отлива каждый день) или суточными (один приливной цикл в день). Два прилива в определенный день обычно не имеют одинаковой высоты (суточное неравенство); это более высокая полная вода и более низкая полная вода в таблицах приливов . Аналогично, два отлива каждый день являются более высокой малой водой и более низкой малой водой . Суточное неравенство не является постоянным и, как правило, невелико, когда Луна находится над экватором . [b]
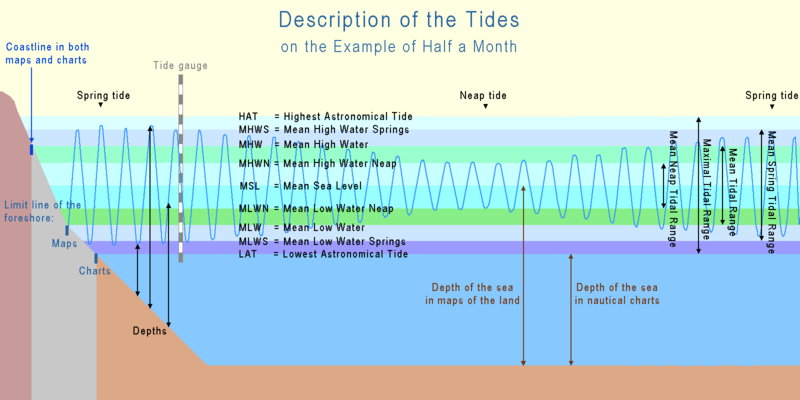
Можно определить следующие контрольные уровни приливов, от самого высокого до самого низкого:

Полусуточный диапазон (разница в высоте между высокой и низкой водой в течение примерно половины дня) изменяется в двухнедельном цикле. Примерно дважды в месяц, около новолуния и полнолуния , когда Солнце, Луна и Земля образуют линию (конфигурация, известная как сизигия [ 7] ), приливная сила, вызванная Солнцем, усиливает ту, что вызвана Луной. Диапазон прилива тогда достигает своего максимума; это называется весенним приливом . Он не назван в честь сезона , но, как и это слово, происходит от значения «прыгать, вырываться, подниматься», как в естественном источнике . Весенние приливы иногда называют приливами сизигии [8] .
Когда Луна находится в первой или третьей четверти, Солнце и Луна разделены на 90°, если смотреть с Земли (в квадратуре ), и солнечная приливная сила частично нейтрализует приливную силу Луны. В эти моменты лунного цикла диапазон прилива минимален; это называется квадратурным приливом , или NEAPS . «Neap» — англосаксонское слово, означающее «без силы», как в forðganges nip (идущий вперед без силы). [9] Квадратурные приливы иногда называют квадратурными приливами . [8]
Весенние приливы приводят к высоким водам выше среднего, низким водам ниже среднего, времени " слабой воды ", которое короче среднего, и более сильным приливным течениям, чем в среднем. Приливы приводят к менее экстремальным приливным условиям. Между приливами и отливами существует примерно семидневный интервал.
Приливные составляющие являются чистым результатом множественных влияний, влияющих на приливные изменения в течение определенных периодов времени. Первичные составляющие включают в себя вращение Земли, положение Луны и Солнца относительно Земли, высоту Луны (возвышение) над экватором Земли и батиметрию . Изменения с периодами менее половины дня называются гармоническими составляющими . И наоборот, циклы дней, месяцев или лет называются долгопериодными составляющими.
Приливные силы воздействуют на всю Землю , но движение твердой Земли происходит всего на сантиметры. Напротив, атмосфера гораздо более жидкая и сжимаемая, поэтому ее поверхность движется на километры, в смысле контурного уровня определенного низкого давления во внешней атмосфере.
В большинстве мест самая большая составляющая — это основная лунная полусуточная составляющая , также известная как приливная составляющая M2 или приливная составляющая M2 . Ее период составляет около 12 часов и 25,2 минут, ровно половина приливных лунных суток , что является средним временем, отделяющим один лунный зенит от другого, и, таким образом, является временем, необходимым для того, чтобы Земля совершила один оборот относительно Луны. Простые приливные часы отслеживают эту составляющую. Лунные сутки длиннее земных, потому что Луна вращается в том же направлении, что и Земля. Это аналогично минутной стрелке на часах, пересекающей часовую стрелку в 12:00, а затем снова примерно в 1:05+1 ⁄ 2 (не в 1:00).
Луна вращается вокруг Земли в том же направлении, в котором Земля вращается вокруг своей оси, поэтому Луне требуется немного больше суток — около 24 часов и 50 минут, чтобы вернуться в то же самое место на небе. За это время она прошла над головой ( кульминация ) один раз и под ногами один раз (под часовым углом 00:00 и 12:00 соответственно), поэтому во многих местах период самого сильного приливного воздействия — это вышеупомянутый, около 12 часов и 25 минут. Момент самого высокого прилива не обязательно наступает, когда Луна находится ближе всего к зениту или надиру , но период воздействия все равно определяет время между приливами.
Поскольку гравитационное поле, создаваемое Луной, ослабевает с расстоянием от Луны, оно оказывает немного большую, чем в среднем, силу на сторону Земли, обращенную к Луне, и немного меньшую силу на противоположную сторону. Таким образом, Луна имеет тенденцию слегка «растягивать» Землю вдоль линии, соединяющей два тела. Твердая Земля немного деформируется, но океанская вода, будучи жидкой, может свободно перемещаться гораздо больше в ответ на приливную силу, особенно горизонтально (см. равновесный прилив ).
По мере вращения Земли величина и направление приливной силы в любой конкретной точке на поверхности Земли постоянно меняются; хотя океан никогда не достигает равновесия — у жидкости никогда нет времени «догнать» состояние, которого она в конечном итоге достигла бы, если бы приливная сила была постоянной — изменяющаяся приливная сила, тем не менее, вызывает ритмичные изменения высоты морской поверхности.

Когда в течение дня происходит два прилива разной высоты (и два отлива также разной высоты), такая картина называется смешанным полусуточным приливом . [11]



Изменение расстояния между Луной и Землей также влияет на высоту приливов. Когда Луна находится ближе всего, в перигее , диапазон увеличивается, а когда она находится в апогее , диапазон сокращается. Шесть или восемь раз в год перигей совпадает либо с новолунием, либо с полнолунием, вызывая перигейские весенние приливы с самым большим приливным диапазоном . Разница между высотой прилива в перигейском весеннем приливе и весенним приливом, когда Луна находится в апогее, зависит от местоположения, но может быть на фут выше. [12]
К ним относятся гравитационные эффекты Солнца, наклон экватора и оси вращения Земли, наклон плоскости лунной орбиты и эллиптическая форма орбиты Земли вокруг Солнца.
Сложный прилив (или прилив) возникает в результате взаимодействия двух исходных волн на мелководье. [13]

Поскольку приливная составляющая M 2 доминирует в большинстве мест, стадия или фаза прилива, обозначаемая временем в часах после прилива, является полезной концепцией. Приливная стадия также измеряется в градусах, с 360° на приливной цикл. Линии постоянной приливной фазы называются котидальными линиями , которые аналогичны контурным линиям постоянной высоты на топографических картах , и при нанесении на карту образуют котидальную карту или котидальную диаграмму . [16] Высокая вода достигается одновременно вдоль котидальных линий, простирающихся от побережья в океан, и котидальные линии (и, следовательно, приливные фазы) продвигаются вдоль побережья. Полусуточные и длинные фазовые составляющие измеряются от прилива, дневные — от максимального прилива. Это и последующее обсуждение в точности верно только для одной приливной составляющей.
Для океана в форме круглого бассейна, ограниченного береговой линией, котидальные линии направлены радиально внутрь и должны в конечном итоге встретиться в общей точке, амфидромической точке . Амфидромическая точка одновременно является котидальной с высокой и низкой водой, что удовлетворяется нулевым приливным движением. (Редкое исключение происходит, когда прилив окружает остров, как это происходит вокруг Новой Зеландии, Исландии и Мадагаскара .) Приливное движение обычно уменьшается по мере удаления от материковых берегов, так что пересечение котидальных линий представляет собой контуры постоянной амплитуды (половина расстояния между высокой и низкой водой), которые уменьшаются до нуля в амфидромической точке. Для полусуточного прилива амфидромическую точку можно рассматривать примерно как центр циферблата часов, при этом часовая стрелка указывает в направлении котидальной линии высокой воды, которая находится прямо напротив котидальной линии низкой воды. Высокая вода вращается вокруг амфидромической точки каждые 12 часов в направлении восходящих котидальных линий и от отступающих котидальных линий. Это вращение, вызванное эффектом Кориолиса , обычно происходит по часовой стрелке в южном полушарии и против часовой стрелки в северном полушарии. Разница между котидальной фазой и фазой эталонного прилива — это эпоха . Эталонный прилив — это гипотетическая составляющая «равновесного прилива» на безземельной Земле, измеренная на долготе 0°, Гринвичском меридиане. [17]
В Северной Атлантике, поскольку котидальные линии циркулируют против часовой стрелки вокруг амфидромической точки, прилив проходит мимо гавани Нью-Йорка примерно на час раньше, чем до гавани Норфолка. К югу от мыса Хаттерас приливные силы более сложны и не могут быть надежно предсказаны на основе котидальных линий Северной Атлантики.
Исследование физики приливов имело важное значение на раннем этапе развития небесной механики , при этом существование двух суточных приливов объяснялось гравитацией Луны. Позднее суточные приливы были более точно объяснены взаимодействием гравитации Луны и Солнца.
Селевк из Селевкии выдвинул теорию около 150 г. до н. э. о том, что приливы вызываются Луной. Влияние Луны на водоемы также упоминается в « Тетрабиблосе » Птолемея . [ c]
В De temporum ratione ( Расчет времени ) 725 года Беда связал полуденные приливы и явление изменения приливной высоты с Луной и ее фазами. Беда начинает с того, что отмечает, что приливы возникают и исчезают на 4/5 часа позже каждый день, так же как Луна восходит и заходит на 4/5 часа позже. [19] Далее он подчеркивает, что за два лунных месяца (59 дней) Луна обходит Землю 57 раз и происходит 114 приливов. [20] Затем Беда замечает, что высота приливов меняется в течение месяца. Увеличивающиеся приливы называются malinae , а уменьшающиеся — ledones , и что месяц делится на четыре части по семь или восемь дней с чередованием malinae и ledones . [21] В том же отрывке он также отмечает влияние ветров на сдерживание приливов. [21] Беда также отмечает, что время приливов варьируется от места к месту. К северу от местонахождения Беды ( Монквермут ) приливы наступают раньше, к югу — позже. [22] Он объясняет, что прилив «оставляет эти берега, чтобы иметь возможность затопить другие [берега], когда он прибудет туда», отмечая, что «Луна, которая сигнализирует о наступлении прилива здесь, сигнализирует о его отступлении в других регионах, далеких от этой четверти неба». [22]
Позднее средневековое понимание приливов основывалось в первую очередь на трудах мусульманских астрономов , которые стали доступны благодаря латинскому переводу, начиная с XII века. [23] Абу Машар аль-Балхи (ум. около 886 г.) в своем труде «Введение в астрономию» учил, что приливы и отливы вызываются Луной. [23] Абу Машар обсуждал влияние ветра и фаз Луны относительно Солнца на приливы. [23] В XII веке аль-Битруджи (ум. около 1204 г.) высказал идею о том, что приливы вызываются общей циркуляцией небес. [23]
Симон Стевин в своей работе 1608 года «De spiegheling der Ebbenvloet» ( «Теория приливов и отливов ») опроверг большое количество заблуждений, которые все еще существовали относительно приливов и отливов. Стевин отстаивал идею о том, что притяжение Луны ответственно за приливы, и ясно говорил об отливах, приливах, весенних приливах и квадратурных приливах , подчеркивая необходимость проведения дальнейших исследований. [24] [25]
В 1609 году Иоганн Кеплер также справедливо предположил, что гравитация Луны вызывает приливы, [d] основываясь на древних наблюдениях и корреляциях.
Галилео Галилей в своем «Диалоге о двух главных мировых системах» 1632 года , рабочее название которого было «Диалог о приливах» , дал объяснение приливов. Однако полученная теория была неверной, поскольку он приписывал приливы выплескиванию воды, вызванному движением Земли вокруг Солнца. Он надеялся предоставить механическое доказательство движения Земли. Ценность его приливной теории оспаривается. Галилей отверг объяснение приливов Кеплером.
Исаак Ньютон (1642–1727) был первым человеком, объяснившим приливы как результат гравитационного притяжения астрономических масс. Его объяснение приливов (и многих других явлений) было опубликовано в Principia ( 1687) [27] [28] и использовал свою теорию всемирного тяготения для объяснения лунного и солнечного притяжения как источника сил, порождающих приливы. [e] Ньютон и другие до Пьера-Симона Лапласа работали над проблемой с точки зрения статической системы (теории равновесия), которая обеспечивала приближение, описывающее приливы, которые возникали бы в неинерциальном океане, равномерно покрывающем всю Землю. [27] Сила, порождающая приливы (или соответствующий ей потенциал ), по-прежнему имеет отношение к приливной теории, но как промежуточная величина (вынуждающая функция), а не как конечный результат; Теория также должна учитывать накопленную динамическую приливную реакцию Земли на приложенные силы, на которую влияют глубина океана, вращение Земли и другие факторы. [29]
В 1740 году Королевская академия наук в Париже учредила премию за лучшее теоретическое эссе о приливах. Даниэль Бернулли , Леонард Эйлер , Колин Маклорен и Антуан Каваллери разделили премию. [30]
Маклорен использовал теорию Ньютона, чтобы показать, что гладкая сфера, покрытая достаточно глубоким океаном под приливной силой одного деформирующего тела, представляет собой вытянутый сфероид (по сути, трехмерный овал) с большой осью, направленной к деформирующему телу. Маклорен был первым, кто написал о влиянии вращения Земли на движение. Эйлер понял, что горизонтальная составляющая приливной силы (больше, чем вертикальная) вызывает прилив. В 1744 году Жан Лерон Д'Аламбер изучал приливные уравнения для атмосферы, которые не включали вращение.
В 1770 году барк Джеймса Кука HMS Endeavour сел на Большой Барьерный Риф . Были предприняты попытки снять его с мели следующим приливом, которые не увенчались успехом, но последующий прилив с легкостью поднял его. Пока судно ремонтировалось в устье реки Индевор, Кук наблюдал за приливами в течение семи недель. Во время квадратурных приливов оба прилива в течение дня были похожи, но во время весенних приливов приливы поднимались на 7 футов (2,1 м) утром и на 9 футов (2,7 м) вечером. [31]
Пьер-Симон Лаплас сформулировал систему дифференциальных уравнений в частных производных, связывающую горизонтальный поток океана с высотой его поверхности, первую крупную динамическую теорию приливов воды. Приливные уравнения Лапласа используются и сегодня. Уильям Томсон, 1-й барон Кельвин , переписал уравнения Лапласа в терминах вихреобразования , что позволило получить решения, описывающие приливно-отливные прибрежные захваченные волны, известные как волны Кельвина . [32] [33] [34]
Другие, включая Кельвина и Анри Пуанкаре , развили теорию Лапласа. Основываясь на этих разработках и лунной теории EW Brown, описывающей движения Луны, Артур Томас Дудсон разработал и опубликовал в 1921 году [35] первую современную разработку потенциала приливов в гармонической форме: Дудсон выделил 388 приливных частот. [36] Некоторые из его методов используются и по сей день. [37]


С древних времен наблюдение за приливами и их обсуждение становились все более сложными, сначала отмечая ежедневную повторяемость, затем связь приливов с Солнцем и Луной. Пифей отправился на Британские острова около 325 г. до н. э. и, по-видимому, был первым, кто связал весенние приливы с фазой Луны.
Во II веке до нашей эры эллинистический астроном Селевк из Селевкии правильно описал явление приливов, чтобы поддержать свою гелиоцентрическую теорию. [38] Он правильно предположил, что приливы были вызваны Луной , хотя он считал, что взаимодействие было опосредовано пневмой . Он отметил, что приливы различаются по времени и силе в разных частях света. Согласно Страбону (1.1.9), Селевк был первым, кто связал приливы с лунным притяжением, и что высота приливов зависит от положения Луны относительно Солнца. [39]
В «Естественной истории» Плиния Старшего собрано множество наблюдений за приливами, например, весенние приливы происходят через несколько дней после (или до) новолуния и полнолуния и достигают наибольшего уровня около равноденствий, хотя Плиний отметил множество связей, которые сейчас считаются фантастическими. В своей « Географии» Страбон описал приливы в Персидском заливе , имеющие наибольший диапазон, когда Луна находится дальше всего от плоскости экватора. Все это несмотря на относительно небольшую амплитуду приливов в бассейне Средиземного моря . (Сильные течения через пролив Эврипа и Мессинский пролив озадачили Аристотеля .) Филострат обсуждал приливы в пятой книге « Жизни Аполлония Тианского ». Филострат упоминает луну, но приписывает приливы «духам». Около 730 года нашей эры в Европе достопочтенный Беда Достопочтенный описал, как прилив на одном побережье Британских островов совпадал с отливом на другом, а также описал временную динамику прилива вдоль побережья Нортумбрии.
Первая таблица приливов в Китае была записана в 1056 году нашей эры, в первую очередь для посетителей, желающих увидеть знаменитую приливную волну в реке Цяньтан . Считается, что первая известная британская таблица приливов принадлежит Джону Уоллингфорду, который умер аббатом Сент-Олбанса в 1213 году, и основана на том, что приливы происходили на 48 минут позже каждый день и на три часа раньше в устье Темзы , чем выше по течению в Лондоне . [40]
В 1614 году Клод д'Аббевиль опубликовал работу « История миссии капуцинов на острове Мараньян и окрестных землях », в которой он показал, что народ тупинамба уже раньше Европы имел представление о связи между Луной и приливами. [41]
Уильям Томсон (лорд Кельвин) руководил первым систематическим гармоническим анализом приливных записей, начиная с 1867 года. Главным результатом стало создание машины для прогнозирования приливов , использующей систему шкивов для сложения шести гармонических временных функций. Она была «запрограммирована» путем переустановки шестеренок и цепей для регулировки фазировки и амплитуд. Подобные машины использовались до 1960-х годов. [42]
Первая известная запись уровня моря за весь цикл весна-прилив была сделана в 1831 году на военно-морском доке в устье Темзы . Во многих крупных портах к 1850 году были автоматические мареографические станции.
Джон Лаббок был одним из первых, кто нанес на карту линии приливов и отливов для Великобритании, Ирландии и прилегающих побережий в 1840 году. [43] Уильям Уэвелл расширил эту работу, завершив ее почти глобальной картой в 1836 году. [44] Чтобы сделать эти карты последовательными, он выдвинул гипотезу о существовании региона без приливных подъемов и падений, где линии приливов и отливов встречаются в середине океана. Существование такой амфидромной точки , как они теперь известны, было подтверждено в 1840 году капитаном Уильямом Хьюиттом, RN , в результате тщательного зондирования в Северном море . [45] [46] [32]
Гораздо позже, в конце 20-го века, геологи заметили приливные ритмиты , которые документируют возникновение древних приливов в геологической летописи, особенно в каменноугольном периоде . [47] [48]
Приливная сила, создаваемая массивным объектом (далее — Луна) на небольшую частицу, находящуюся на обширном теле или внутри него (далее — Земля), представляет собой векторную разность между гравитационной силой, действующей со стороны Луны на частицу, и гравитационной силой, которая действовала бы на частицу, если бы она находилась в центре масс Земли.
В то время как сила тяготения, действующая на Землю со стороны небесного тела, обратно пропорциональна квадрату его расстояния до Земли, максимальная приливная сила обратно пропорциональна, приблизительно, кубу этого расстояния. [49] Если бы приливная сила, создаваемая каждым телом, была бы равна его полной силе тяготения (что не так из-за свободного падения всей Земли, а не только океанов, к этим телам), наблюдалась бы другая картина приливных сил, например, при гораздо более сильном влиянии Солнца, чем Луны: солнечная сила тяготения на Земле в среднем в 179 раз сильнее лунной, но поскольку Солнце в среднем в 389 раз дальше от Земли, градиент его поля слабее. Общая пропорциональность такова:
где M — масса небесного тела, d — его расстояние, ρ — его средняя плотность, а r — его радиус. Отношение r / d связано с углом, образуемым объектом на небе. Поскольку Солнце и Луна имеют практически одинаковый диаметр на небе, приливная сила Солнца меньше, чем у Луны, поскольку его средняя плотность намного меньше, и она составляет всего 46% от лунной, [f] таким образом, во время весеннего прилива вклад Луны составляет 69%, а вклад Солнца — 31%. Точнее, лунное приливное ускорение (вдоль оси Луна–Земля, на поверхности Земли) составляет около 1,1 × 10−7 g , в то время как солнечное приливное ускорение (вдоль оси Солнце–Земля, на поверхности Земли) составляет около 0,52 × 10−7 g , где g — гравитационное ускорение на поверхности Земли. [g] Влияние других планет меняется в зависимости от их расстояний от Земли. Когда Венера находится ближе всего к Земле, ее влияние составляет 0,000113 от солнечного влияния. [50] В другие времена Юпитер или Марс могут оказывать наибольшее влияние.

Поверхность океана аппроксимируется поверхностью, называемой геоидом , которая учитывает силу тяготения, оказываемую Землей, а также центробежную силу из-за вращения. Теперь рассмотрим влияние массивных внешних тел, таких как Луна и Солнце. Эти тела обладают сильными гравитационными полями, которые уменьшаются с расстоянием и заставляют поверхность океана отклоняться от геоида. Они устанавливают новую равновесную поверхность океана, которая выпячивается к Луне с одной стороны и от Луны с другой стороны. Вращение Земли относительно этой формы вызывает суточный приливной цикл. Поверхность океана стремится к этой равновесной форме, которая постоянно меняется и никогда не достигает ее полностью. Когда поверхность океана не выровнена с ней, это как если бы поверхность была наклонной, и вода ускоряется в направлении вниз по склону.
Равновесный прилив — это идеализированный прилив, предполагающий безземельную Землю. [51] Он создал бы приливную выпуклость в океане, вытянутую в сторону притягивающего тела (Луны или Солнца). Он не вызван вертикальным натяжением, ближайшим или дальним от тела, которое очень слабое; скорее, он вызван тангенциальной или тяговой приливной силой, которая сильнее всего примерно в 45 градусах от тела, что приводит к горизонтальному приливному течению. [h] [i] [j] [55]
Глубины океана намного меньше его горизонтальной протяженности. Таким образом, реакция на приливное воздействие может быть смоделирована с использованием приливных уравнений Лапласа , которые включают следующие особенности:
Граничные условия подразумевают отсутствие потока вдоль береговой линии и свободное скольжение на дне.
Эффект Кориолиса (сила инерции) направляет потоки, движущиеся к экватору, на запад, а потоки, движущиеся от экватора, на восток, что позволяет прибрежным волнам задерживаться. Наконец, можно добавить термин диссипации, который является аналогом вязкости.
Теоретическая амплитуда океанических приливов, вызванных Луной, составляет около 54 сантиметров (21 дюйм) в самой высокой точке, что соответствует амплитуде, которая была бы достигнута, если бы океан имел однородную глубину, не было бы суши, а Земля вращалась в такт с орбитой Луны. Солнце также вызывает приливы, теоретическая амплитуда которых составляет около 25 сантиметров (9,8 дюйма) (46% от амплитуды Луны) с периодом цикла 12 часов. Во время весеннего прилива эти два эффекта суммируются до теоретического уровня в 79 сантиметров (31 дюйм), в то время как во время квадратурного прилива теоретический уровень уменьшается до 29 сантиметров (11 дюймов). Поскольку орбиты Земли вокруг Солнца и Луны вокруг Земли являются эллиптическими, приливные амплитуды несколько изменяются в результате изменения расстояний Земля-Солнце и Земля-Луна. Это вызывает изменение приливной силы и теоретической амплитуды около ±18% для Луны и ±5% для Солнца. Если бы и Солнце, и Луна находились в своих самых близких положениях и выровнялись в новолуние, теоретическая амплитуда достигла бы 93 сантиметров (37 дюймов).
Реальные амплитуды значительно различаются не только из-за изменений глубины и континентальных препятствий, но и потому, что распространение волн через океан имеет естественный период того же порядка величины, что и период вращения: если бы не было земельных массивов, то для распространения длинноволновой поверхностной волны вдоль экватора на полпути вокруг Земли потребовалось бы около 30 часов (для сравнения, литосфера Земли имеет естественный период около 57 минут). Земные приливы , которые поднимают и опускают дно океана, и собственное гравитационное притяжение прилива являются существенными и еще больше усложняют реакцию океана на приливные силы.
Приливные колебания Земли вызывают рассеяние со средней скоростью около 3,75 тераватт . [56] Около 98% этого рассеяния происходит за счет морских приливных движений. [57] Рассеивание возникает, когда приливные течения в масштабе бассейна приводят в движение более мелкие потоки, которые испытывают турбулентное рассеяние. Это приливное сопротивление создает крутящий момент на Луне, который постепенно передает угловой момент на ее орбиту и постепенно увеличивает расстояние между Землей и Луной. Равный и противоположный крутящий момент на Земле соответственно уменьшает ее скорость вращения. Таким образом, с течением геологического времени Луна отдаляется от Земли примерно на 3,8 сантиметра (1,5 дюйма) в год, удлиняя земные сутки. [k]
Длина дня увеличилась примерно на 2 часа за последние 600 миллионов лет. Если предположить (в качестве грубого приближения), что скорость замедления была постоянной, то это означало бы, что 70 миллионов лет назад длина дня была примерно на 1% короче, примерно на 4 дня в году больше.

Форма береговой линии и дна океана изменяет способ распространения приливов, поэтому не существует простого общего правила, которое предсказывает время высокой воды по положению Луны на небе. Характеристики побережья, такие как подводная батиметрия и форма береговой линии, означают, что индивидуальные характеристики местоположения влияют на прогнозирование приливов; фактическое время и высота высокой воды могут отличаться от прогнозов модели из-за влияния прибрежной морфологии на приливной поток. Однако для данного местоположения связь между высотой Луны и временем прилива или отлива ( лунный приливный интервал ) является относительно постоянной и предсказуемой, как и время прилива или отлива относительно других точек на том же побережье. Например, прилив в Норфолке, Вирджиния , США, предсказуемо происходит примерно за два с половиной часа до того, как Луна проходит прямо над головой.
Массивы суши и океанические бассейны действуют как барьеры для воды, свободно перемещающейся по всему земному шару, и их различные формы и размеры влияют на величину приливных частот. В результате приливные модели различаются. Например, в США на Восточном побережье преобладают полусуточные приливы, как и на атлантическом побережье Европы, в то время как на Западном побережье преобладают смешанные приливы. [59] [60] [61] Человеческие изменения ландшафта также могут существенно изменить местные приливы. [62]

Приливные силы, вызванные Луной и Солнцем, создают очень длинные волны, которые распространяются по всему океану, следуя путям, показанным на картах приливов и отливов. Время, когда гребень волны достигает порта, затем дает время высокой воды в порту. Время, необходимое волне для прохождения океана, также означает, что существует задержка между фазами Луны и их влиянием на прилив. Например, весны и качки в Северном море отстают на два дня от новолуния/полнолуния и первой/третьей четверти луны. Это называется возрастом прилива . [63] [64]
Батиметрия океана сильно влияет на точное время и высоту прилива в конкретной прибрежной точке. Существуют некоторые экстремальные случаи; залив Фанди на восточном побережье Канады часто считается местом с самыми высокими приливами в мире из-за его формы, батиметрии и расстояния от края континентального шельфа. [65] Измерения, проведенные в ноябре 1998 года в Бернткоут-Хед в заливе Фанди, зафиксировали максимальный диапазон 16,3 метра (53 фута) и наивысший прогнозируемый экстремум 17 метров (56 футов). [66] [67] Аналогичные измерения, проведенные в марте 2002 года в Лиф-Бейсин, залив Унгава в северной части Квебека, дали схожие значения (с учетом погрешностей измерений), максимальный диапазон 16,2 метра (53 фута) и наивысший прогнозируемый экстремум 16,8 метра (55 футов). [66] [67] Залив Унгава и залив Фанди находятся на одинаковом расстоянии от края континентального шельфа, но залив Унгава свободен от пакового льда только около четырех месяцев в году, тогда как залив Фанди замерзает редко.
В Саутгемптоне в Соединенном Королевстве наблюдается двойной прилив, вызванный взаимодействием приливных составляющих M 2 и M 4 (мелководные приливы основных лунных). [68] В Портленде наблюдается двойной отлив по той же причине. Прилив M 4 наблюдается по всему южному побережью Соединенного Королевства, но его влияние наиболее заметно между островом Уайт и Портлендом , поскольку прилив M 2 является самым низким в этом регионе.
Поскольку режимы колебаний Средиземного и Балтийского морей не совпадают ни с одним значительным астрономическим периодом воздействия, самые большие приливы происходят вблизи их узких соединений с Атлантическим океаном. Чрезвычайно малые приливы также происходят по той же причине в Мексиканском заливе и Японском море . В других местах, как вдоль южного побережья Австралии , отливы могут быть вызваны наличием близлежащего амфидрома .

Теория гравитации Исаака Ньютона впервые позволила объяснить, почему в день обычно бывает два прилива, а не один, и дала надежду на детальное понимание приливных сил и поведения. Хотя может показаться, что приливы можно предсказать с помощью достаточно подробных знаний мгновенных астрономических воздействий, фактический прилив в данном месте определяется астрономическими силами, накопленными водоемом за многие дни. Кроме того, для точных результатов потребуются подробные знания о форме всех океанических бассейнов — их батиметрии и форме береговой линии.
Текущая процедура анализа приливов следует методу гармонического анализа, введенному в 1860-х годах Уильямом Томсоном . Он основан на принципе, что астрономические теории движений Солнца и Луны определяют большое количество частот компонентов, и на каждой частоте есть компонент силы, стремящийся вызвать приливное движение, но что в каждом интересующем месте на Земле приливы реагируют на каждой частоте с амплитудой и фазой, свойственными этой местности. Поэтому в каждом интересующем месте высоты приливов измеряются в течение достаточно длительного периода времени (обычно более года в случае нового порта, ранее не изученного), чтобы можно было различить с помощью анализа реакцию на каждой значительной частоте, генерирующей приливы, и извлечь приливные константы для достаточного количества самых сильных известных компонентов астрономических приливных сил, чтобы обеспечить практическое прогнозирование приливов. Ожидается, что высоты приливов будут следовать за приливной силой с постоянной амплитудой и фазовой задержкой для каждого компонента. Поскольку астрономические частоты и фазы можно рассчитать с точностью, можно предсказать высоту прилива в другое время, как только будет найдена реакция на гармонические компоненты астрономических сил, генерирующих приливы.
Основные закономерности приливов и отливов:
Самый высокий астрономический прилив — это перигейный весенний прилив, когда Солнце и Луна находятся ближе всего к Земле.
При столкновении с периодически изменяющейся функцией стандартный подход заключается в использовании рядов Фурье , формы анализа, которая использует синусоидальные функции в качестве базисного набора, имея частоты, которые в ноль, один, два, три и т. д. раз больше частоты конкретного основного цикла. Эти кратные называются гармониками основной частоты, а процесс называется гармоническим анализом . Если базисный набор синусоидальных функций подходит для моделируемого поведения, необходимо добавить относительно немного гармонических членов. Орбитальные пути очень близки к круговым, поэтому синусоидальные вариации подходят для приливов.
Для анализа высоты прилива подход с использованием ряда Фурье на практике должен быть более сложным, чем использование одной частоты и ее гармоник. Приливные паттерны разлагаются на множество синусоид, имеющих множество основных частот, соответствующих (как в лунной теории ) множеству различных комбинаций движений Земли, Луны и углов, которые определяют форму и местоположение их орбит.
Для приливов, таким образом, гармонический анализ не ограничивается гармониками одной частоты. [l] Другими словами, гармонии являются кратными многих основных частот, а не только основной частоты более простого подхода ряда Фурье. Их представление в виде ряда Фурье, имеющего только одну основную частоту и ее (целые) кратные, потребовало бы многих членов и было бы сильно ограничено во временном диапазоне, для которого оно было бы действительным.
Изучение высоты прилива методом гармонического анализа было начато Лапласом, Уильямом Томсоном (лорд Кельвин) и Джорджем Дарвином . А. Т. Дудсон расширил их работу, введя обозначение числа Дудсона для организации сотен результирующих членов. Этот подход с тех пор стал международным стандартом, и осложнения возникают следующим образом: сила, поднимающая прилив, теоретически задается суммой нескольких членов. Каждый член имеет вид
где
Существует один термин для Луны и второй термин для Солнца. Фаза p первой гармоники для термина Луны называется лунным приливным интервалом или интервалом высокой воды.
Следующее уточнение заключается в том, чтобы учесть гармонические члены, обусловленные эллиптической формой орбит. Для этого значение амплитуды принимается не постоянным, а изменяющимся со временем, около средней амплитуды A o . Для этого замените A o в приведенном выше уравнении на A ( t ), где A — другая синусоида, похожая на циклы и эпициклы теории Птолемея . Это дает
то есть среднее значение A o с синусоидальным изменением вокруг него величины A a , с частотой ω a и фазой p a . Подстановка этого вместо A o в исходное уравнение дает произведение двух косинусных множителей:
Учитывая, что для любых x и y
ясно, что составной член, включающий произведение двух косинусных членов, каждый со своей собственной частотой, равен трем простым косинусным членам, которые должны быть сложены на исходной частоте, а также на частотах, которые являются суммой и разностью двух частот члена произведения. (Три, а не два члена, поскольку все выражение равно .) Рассмотрим далее, что приливная сила в месте зависит также от того, находится ли Луна (или Солнце) выше или ниже плоскости экватора, и что эти атрибуты имеют свои собственные периоды, также несоизмеримые с днем и месяцем, и ясно, что получается много комбинаций. При тщательном выборе основных астрономических частот число Дудсона аннотирует конкретные добавления и разности, чтобы сформировать частоту каждого простого косинусного члена.
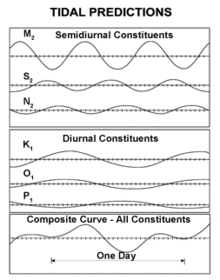
Помните, что астрономические приливы не включают погодные эффекты. Кроме того, изменения местных условий (движение песчаной отмели, углубление устьев гаваней и т. д.) вдали от преобладающих во время измерения условий влияют на фактическое время и величину прилива. Организации, ссылающиеся на «самый высокий астрономический прилив» для какого-либо местоположения, могут преувеличивать эту цифру в качестве фактора безопасности в отношении аналитических неопределенностей, расстояния от ближайшей точки измерения, изменений с момента последнего наблюдения, проседания грунта и т. д., чтобы избежать ответственности в случае превышения инженерных работ. Особая осторожность необходима при оценке размера «погодного нагона» путем вычитания астрономического прилива из наблюдаемого прилива.
Тщательный анализ данных Фурье за девятнадцатилетний период ( Национальная эпоха приливных данных в США) использует частоты, называемые приливными гармоническими составляющими . Девятнадцать лет предпочтительны, потому что относительные положения Земли, Луны и Солнца повторяются почти точно в 19-летнем цикле Метона , который достаточно длинный, чтобы включить 18,613-летнюю лунную узловую приливную составляющую . Этот анализ можно выполнить, используя только знание периода воздействия , но без детального понимания математического вывода, что означает, что полезные приливные таблицы строились на протяжении столетий. [69] Полученные амплитуды и фазы затем можно использовать для прогнозирования ожидаемых приливов. Обычно они доминируют составляющими около 12 часов ( полусуточные составляющие), но есть также основные составляющие около 24 часов ( суточные ). Более долгосрочные составляющие - 14-дневные или двухнедельные , ежемесячные и полугодовые. Полусуточные приливы доминируют на побережье, но некоторые области, такие как Южно-Китайское море и Мексиканский залив, являются в основном суточными. В полусуточных областях основные составляющие M 2 (лунный) и S 2 (солнечный) периоды немного отличаются, так что относительные фазы, а следовательно, и амплитуда объединенного прилива, меняются каждые две недели (14-дневный период). [70]
На графике M 2 выше каждая котидальная линия отличается на один час от своих соседей, а более толстые линии показывают приливы в фазе с равновесием в Гринвиче. Линии вращаются вокруг амфидромических точек против часовой стрелки в северном полушарии, так что от полуострова Нижняя Калифорния до Аляски и от Франции до Ирландии прилив M 2 распространяется на север. В южном полушарии это направление по часовой стрелке. С другой стороны, прилив M 2 распространяется против часовой стрелки вокруг Новой Зеландии, но это потому, что острова действуют как плотина и позволяют приливам иметь разную высоту на противоположных сторонах островов. (Приливы распространяются на север на восточной стороне и на юг на западном побережье, как и предсказывает теория.)
Исключением является пролив Кука , где приливные течения периодически связывают высокую и низкую воду. Это происходит потому, что котидальные линии 180° вокруг амфидромов находятся в противофазе, например, высокая вода напротив низкой воды на каждом конце пролива Кука. Каждая приливная составляющая имеет различный рисунок амплитуд, фаз и амфидромных точек, поэтому рисунки M 2 не могут использоваться для других приливных компонентов.




Поскольку Луна движется по своей орбите вокруг Земли и в том же направлении, что и вращение Земли, точка на Земле должна повернуться немного дальше, чтобы догнать, так что время между полусуточными приливами составляет не двенадцать, а 12,4206 часов — чуть больше двадцати пяти минут. Два пика не равны. Два прилива в день чередуются по максимальной высоте: более низкий максимум (чуть меньше трех футов), более высокий максимум (чуть больше трех футов) и снова более низкий максимум. То же самое касается отливов.
Когда Земля, Луна и Солнце находятся на одной линии (Солнце–Земля–Луна или Солнце–Луна–Земля), два основных влияния объединяются, чтобы произвести весенние приливы; когда две силы противостоят друг другу, как когда угол Луна–Земля–Солнце близок к девяноста градусам, возникают квадратурные приливы. По мере того, как Луна движется по своей орбите, она меняется с севера на юг от экватора. Чередование высот приливов становится меньше, пока они не станут одинаковыми (в лунное равноденствие Луна находится над экватором), затем снова развивается, но с другой полярностью, увеличиваясь до максимальной разницы, а затем снова уменьшаясь.
Влияние приливов на течение или поток гораздо сложнее анализировать, а данные собирать гораздо сложнее. Высота прилива — скалярная величина , плавно изменяющаяся в широком регионе. Поток — векторная величина , имеющая величину и направление, которые могут существенно меняться в зависимости от глубины и на коротких расстояниях из-за местной батиметрии. Кроме того, хотя центр водного канала является наиболее полезным местом измерения, моряки возражают, когда оборудование для измерения течения загромождает водные пути. Поток, текущий вверх по изогнутому каналу, может иметь схожую величину, хотя его направление непрерывно меняется вдоль канала. Удивительно, но потоки прилива и отлива часто не имеют противоположных направлений. Направление потока определяется формой канала вверх по течению, а не формой канала вниз по течению. Аналогично, водовороты могут образовываться только в одном направлении потока.
Тем не менее, анализ приливных течений похож на анализ приливных высот: в простом случае в данном месте поток прилива в основном направлен в одном направлении, а отлив — в другом. Скорости прилива имеют положительный знак, а скорости отлива — отрицательный. Анализ выполняется так, как будто это высоты прилива.
В более сложных ситуациях основные приливы и отливы не доминируют. Вместо этого направление и величина потока описывают эллипс над приливным циклом (на полярном графике), а не вдоль линий приливов и отливов. В этом случае анализ может проводиться по парам направлений, при этом первичные и вторичные направления находятся под прямым углом. Альтернативой является рассмотрение приливных потоков как комплексных чисел, поскольку каждое значение имеет как величину, так и направление.
Информация о приливных течениях чаще всего встречается на морских картах , представленных в виде таблицы скоростей течения и пеленгов с часовыми интервалами, с отдельными таблицами для весенних и квадратурных приливов. Время определяется относительно высокой воды в какой-либо гавани, где приливное поведение имеет схожий характер, хотя оно может быть и далеко.
Как и в случае с прогнозами высоты приливов, прогнозы приливных течений, основанные только на астрономических факторах, не учитывают погодные условия, которые могут полностью изменить результат.
Приливной поток через пролив Кука между двумя главными островами Новой Зеландии особенно интересен, так как приливы по обе стороны пролива почти точно не совпадают по фазе, так что прилив одной стороны совпадает с отливом другой. В результате возникают сильные течения с почти нулевым изменением приливной высоты в центре пролива. Тем не менее, хотя приливная волна обычно течет в одном направлении в течение шести часов и в обратном направлении в течение шести часов, конкретная волна может длиться восемь или десять часов, а обратная волна ослабевает. В особенно бурных погодных условиях обратная волна может быть полностью преодолена, так что поток продолжит движение в том же направлении в течение трех или более периодов волны.
Еще одним осложнением для течения пролива Кука является то, что прилив на южной стороне (например, в Нельсоне ) следует общему двухнедельному циклу весенне-квадратурного прилива (как и на западной стороне страны), но приливная схема северной стороны имеет только один цикл в месяц, как и на восточной стороне: Веллингтон и Нейпир .
График приливов пролива Кука показывает отдельно высоту и время высокой и низкой воды по ноябрь 2007 года; это не измеренные значения, а вместо этого рассчитанные на основе приливных параметров, полученных из многолетних измерений. Навигационная карта пролива Кука содержит информацию о приливных течениях. Например, издание за январь 1979 года для 41°13.9′S 174°29.6′E / 41.2317°S 174.4933°E / -41.2317; 174.4933 (к северо-западу от мыса Теравити ) относит время к Уэстпорту , тогда как выпуск за январь 2004 года относится к Веллингтону. Около мыса Теравити в середине пролива Кука изменение высоты прилива почти равно нулю, а приливное течение достигает своего максимума, особенно вблизи печально известного рифа Карори. Помимо погодных условий, на фактические течения через пролив Кука влияют различия в высоте прилива между двумя концами пролива, и, как можно видеть, только один из двух весенних приливов на северо-западном конце пролива около Нельсона имеет аналогичный весенний прилив на юго-восточном конце (Веллингтон), поэтому результирующее поведение не соответствует ни одной из контрольных гаваней. [ необходима ссылка ]
Приливную энергию можно извлекать двумя способами: вставляя водяную турбину в приливное течение или строя пруды, которые выпускают/впускают воду через турбину. В первом случае количество энергии полностью определяется временем и величиной приливного течения. Однако наилучшие течения могут быть недоступны, поскольку турбины будут препятствовать кораблям. Во втором случае строительство плотин-запрудов обходится дорого, полностью нарушаются естественные водные циклы, нарушается судоходство. Однако при наличии нескольких прудов электроэнергия может вырабатываться в выбранное время. До сих пор установлено мало систем для приливной генерации (наиболее известная из них — La Rance в Сен-Мало , Франция), которые сталкиваются со многими трудностями. Помимо экологических проблем, простое противостояние коррозии и биологическому обрастанию представляет собой инженерные проблемы.
Сторонники приливной энергетики отмечают, что, в отличие от ветровых электростанций, уровни генерации можно надежно предсказать, за исключением погодных условий. Хотя некоторая генерация возможна в течение большей части приливного цикла, на практике турбины теряют эффективность при более низких рабочих скоростях. Поскольку мощность, доступная из потока, пропорциональна кубу скорости потока, периоды, в течение которых возможна высокая генерация энергии, кратковременны.

Приливные течения важны для навигации, и если их не учитывать, возникают значительные ошибки в определении местоположения. Также важны приливные высоты; например, многие реки и гавани имеют мелкий «бар» на входе, который не позволяет лодкам со значительной осадкой заходить во время отлива.
До появления автоматизированной навигации, компетентность в расчете приливных эффектов была важна для морских офицеров. Сертификат экзамена для лейтенантов Королевского флота однажды заявил, что будущий офицер способен «изменять свои приливы». [71]
Время и скорость приливных течений отображаются на картах приливов или в атласе приливных течений . Карты приливов поставляются в наборах. Каждая карта охватывает один час между одним приливом и другим (они игнорируют оставшиеся 24 минуты) и показывают средний приливный поток за этот час. Стрелка на карте приливов указывает направление и среднюю скорость потока (обычно в узлах ) для весенних и квадратурных приливов. Если карта приливов недоступна, на большинстве морских карт есть « приливные ромбы », которые связывают определенные точки на карте с таблицей, дающей направление и скорость приливного потока.
Стандартная процедура противодействия приливным эффектам в навигации заключается в следующем: (1) вычислить " точное счисление " положения (или DR) из расстояния и направления движения, (2) отметить карту (вертикальным крестом, похожим на знак плюс) и (3) провести линию от DR в направлении прилива. Расстояние, на которое прилив перемещает лодку вдоль этой линии, вычисляется с помощью приливной скорости, и это дает "оценочное положение" или EP (традиционно обозначенное точкой в треугольнике).

Морские карты отображают «картированную глубину» воды в определенных местах с « промерами » и использованием батиметрических контурных линий для изображения формы подводной поверхности. Эти глубины относятся к « базисной точке карты », которая обычно является уровнем воды при самом низком возможном астрономическом приливе (хотя обычно используются и другие базисные точки, особенно исторически, и приливы могут быть ниже или выше по метеорологическим причинам) и, следовательно, являются минимально возможной глубиной воды во время приливного цикла. «Высоты высыхания» также могут быть показаны на карте, которые являются высотами открытого морского дна при самом низком астрономическом приливе.
Таблицы приливов и отливов содержат данные о высоте и времени прилива и отлива за каждый день. Чтобы рассчитать фактическую глубину воды, добавьте указанную на карте глубину к опубликованной высоте прилива. Глубину для других времен можно получить из опубликованных приливных кривых для крупных портов. Правило двенадцатых может быть достаточным, если точная кривая недоступна. Это приближение предполагает, что увеличение глубины за шесть часов между низкой и высокой водой составляет: первый час — 1/12, второй — 2/12, третий — 3/12, четвертый — 3/12, пятый — 2/12, шестой — 1/12.

Приливно-отливная экология — это изучение экосистем между линиями низкого и высокого уровня воды вдоль берега. При низкой воде приливно-отливная зона обнажается (или всплывает ), тогда как при высокой воде она находится под водой (или погружена ). Поэтому приливно-отливные экологи изучают взаимодействия между приливно-отливными организмами и их средой, а также между различными видами . Наиболее важные взаимодействия могут различаться в зависимости от типа приливно-отливного сообщества. Самые широкие классификации основаны на субстратах — каменистый берег или мягкое дно.
Литоральные организмы сталкиваются с крайне изменчивой и часто враждебной средой и приспособились справляться с этими условиями и даже использовать их. Одной из легко заметных особенностей является вертикальная зональность , в которой сообщество делится на отдельные горизонтальные полосы определенных видов на каждой высоте над уровнем моря. Способность вида справляться с высыханием определяет его верхний предел, в то время как конкуренция с другими видами устанавливает его нижний предел.
Люди используют приливно-отливные зоны для еды и отдыха. Чрезмерная эксплуатация может нанести прямой ущерб приливно-отливным зонам. Другие антропогенные действия, такие как внедрение инвазивных видов и изменение климата , имеют большие негативные последствия. Морские охраняемые территории являются одним из вариантов, к которому сообщества могут обратиться для защиты этих зон и содействия научным исследованиям .
Приблизительно 12-часовой и двухнедельный приливной цикл оказывает большое влияние на приливные [72] и морские организмы. [73] Следовательно, их биологические ритмы , как правило, происходят в грубых кратных этих периодах. [74] Многие другие животные, такие как позвоночные , демонстрируют схожие циркумприливные ритмы. [75] Примерами являются беременность и вылупление яиц. У людей менструальный цикл длится примерно один лунный месяц , четное кратное приливному периоду. Такие параллели, по крайней мере, намекают на общее происхождение всех животных от морского предка. [76]
Приливные течения, колеблясь в стратифицированном океаническом потоке над неровным рельефом дна, генерируют внутренние волны с приливными частотами. Такие волны называются внутренними приливами .
Мелководные участки в открытой воде могут испытывать вращающиеся приливные течения, текущие в направлениях, которые постоянно меняются, и, таким образом, направление течения (а не сам поток) совершает полный оборот за 12+1 ⁄ 2 часа (например, Нантакет Шолс ). [77]
В дополнение к океаническим приливам, большие озера могут испытывать небольшие приливы, и даже планеты могут испытывать атмосферные приливы и земные приливы . Это непрерывные механические явления. Первые два происходят в жидкостях . Третье влияет на тонкую твердую кору Земли , окружающую ее полужидкие недра (с различными модификациями).
В крупных озерах, таких как Верхнее и Эри, приливы могут достигать 1–4 см (0,39–1,6 дюйма), но они могут быть замаскированы метеорологическими явлениями, такими как сейши . [78] Прилив в озере Мичиган описывается как 1,3–3,8 см (0,5–1,5 дюйма) [79] или 4,4 см ( 1+3 ⁄ 4 дюйма). [80] Это настолько мало, что другие более крупные эффекты полностью маскируют любой прилив, и поэтому эти озера считаются неприливными. [81]
Атмосферные приливы незначительны на уровне земли и на высотах полета, поскольку они замаскированы гораздо более важными погодными эффектами. Атмосферные приливы имеют как гравитационное, так и термическое происхождение и являются доминирующей динамикой на высоте от 80 до 120 километров (от 50 до 75 миль), выше которой молекулярная плотность становится слишком низкой для поддержания поведения жидкости.
Земные приливы или земные приливы влияют на всю массу Земли, которая действует подобно жидкому гироскопу с очень тонкой корой. Земная кора смещается (внутрь/наружу, восток/запад, север/юг) в ответ на лунную и солнечную гравитацию, океанские приливы и атмосферную нагрузку. Хотя это незначительно для большинства видов человеческой деятельности, полусуточная амплитуда земных приливов может достигать около 55 сантиметров (22 дюйма) на экваторе — 15 сантиметров (5,9 дюйма) из-за Солнца — что важно для калибровки GPS и измерений VLBI . Точные астрономические угловые измерения требуют знания скорости вращения Земли и движения полюсов , на оба из которых влияют земные приливы. Полусуточные земные приливы M 2 почти совпадают по фазе с Луной с задержкой около двух часов. [ необходима цитата ]
Галактические приливы — это приливные силы, которые галактики оказывают на звезды внутри них и галактики-спутники, вращающиеся вокруг них. Считается, что воздействие галактических приливов на облако Оорта Солнечной системы вызывает90 процентов долгопериодических комет. [82]
Цунами , большие волны, возникающие после землетрясений, иногда называют приливными волнами , но это название дано из-за их сходства с приливом, а не из-за какой-либо причинно-следственной связи с приливом. Другие явления, не связанные с приливами, но использующие слово прилив, — это отбойная волна , штормовой прилив , ураганный прилив и черные или красные приливы . Многие из этих употреблений являются историческими и относятся к более раннему значению прилива как «часть времени, сезона» и «поток, течение или наводнение». [83]
{{cite book}}: |work=проигнорировано ( помощь ){{cite journal}}: Цитировать журнал требует |journal=( помощь ){{cite web}}: CS1 maint: несколько имен: список авторов ( ссылка )