
Как переходящий праздник , [1] [2] дата Пасхи определяется в каждом году с помощью расчета, известного как computus ( лат . «вычисление»). [3] Пасха празднуется в первое воскресенье после пасхального полнолуния (математическое приближение первого астрономического полнолуния , 21 марта или позже — само по себе фиксированное приближение мартовского равноденствия ). Определение этой даты заранее требует корреляции между лунными месяцами и солнечным годом , а также учета месяца, даты и дня недели юлианского или григорианского календаря . [4] Сложность алгоритма возникает из-за желания связать дату Пасхи с датой еврейского праздника Песах , который, как верят христиане, приходится на время распятия Иисуса. [5]
Первоначально для всей христианской церкви было возможно получать дату Пасхи каждый год через ежегодное объявление папы . Однако к началу третьего века коммуникации в Римской империи ухудшились до такой степени, что церковь придавала большое значение системе, которая позволяла бы духовенству самостоятельно определять дату, независимо, но последовательно. [6] Кроме того, церковь хотела устранить зависимость от еврейского календаря , выведя дату Пасхи непосредственно из мартовского равноденствия. [7]
В «Расчете времени» (725) Беда использует computus как общий термин для любого вида расчета, хотя он называет пасхальные циклы Феофила « пасхальным computus ». К концу VIII века computus стал относиться конкретно к расчету времени. [8] Расчеты дают разные результаты в зависимости от того, используется ли юлианский или григорианский календарь. По этой причине католическая церковь и протестантские церкви (которые следуют григорианскому календарю) празднуют Пасху в другую дату, чем Восточная и Восточная Православная (которые следуют юлианскому календарю). Именно смещение 21 марта от наблюдаемого равноденствия привело к григорианской реформе календаря , чтобы привести их в соответствие.
Пасха отмечает воскресение Иисуса , которое, как верят христиане, произошло на третий день (включительно) после начала Песаха . В еврейском лунно-солнечном календаре Песах начинается в сумерках 14-го дня Нисана . [9] [10] Нисан — первый месяц весны в северном полушарии , 14-е число соответствует полнолунию. Ко II веку многие христиане решили отмечать Пасху только в воскресенье. [11] Еврейский календарь не имеет простой связи с христианскими календарями : он повторно синхронизируется с солнечным годом, вставляя високосный месяц каждые два или три года перед лунным новым годом 1 Нисана . Позднее евреи приняли метонов цикл для прогнозирования будущих вставок .
Возможным следствием этой интеркаляции является то, что 14 нисана может наступить до равноденствия, что некоторые христиане третьего века считали неприемлемым (это не может произойти в фиксированном календаре, используемом сегодня). [12] Следовательно, было решено отделить датировку Пасхи от еврейского календаря, определив первое полнолуние после мартовского равноденствия. Ко времени Первого Никейского собора (325 г. н. э.) Александрийская церковь определила 21 марта как церковную дату равноденствия, независимо от фактических астрономических наблюдений. В 395 г. Феофил опубликовал таблицу будущих дат Пасхи, подтвердив александрийские критерии. [13] После этого computus стал процедурой определения первого воскресенья после первого церковного полнолуния , выпадающего на 21 марта или после этой даты.
Самые ранние известные римские таблицы были разработаны в 222 году Ипполитом Римским на основе восьмилетних циклов. Затем 84-летние таблицы были введены в Риме Августалисом около конца 3-го века. [a] Хотя процесс, основанный на 19-летнем метоновом цикле, был впервые предложен епископом Анатолием Лаодикийским около 277 года, эта концепция не была полностью принята, пока александрийский метод не стал авторитетным в конце 4-го века. [b]
Александрийский компутус был преобразован из александрийского календаря в юлианский в Александрии около 440 года, что привело к появлению пасхальной таблицы (приписываемой папе Кириллу Александрийскому ), охватывающей годы с 437 по 531 год. [16] Эта пасхальная таблица была источником, который вдохновил Дионисия Малого , работавшего в Риме примерно с 500 по 540 год, [17] на создание ее продолжения в форме его знаменитой пасхальной таблицы, охватывающей годы с 532 по 616 год. [18] Дионисий ввел христианскую эру (считая годы от Воплощения Христа), опубликовав эту новую пасхальную таблицу в 525 году. [19] [c]
Модифицированный 84-летний цикл был принят в Риме в первой половине IV века. Викторий Аквитанский попытался адаптировать александрийский метод к римским правилам в 457 году в форме 532-летней таблицы, но он внес серьезные ошибки. [20] Эти викторианские таблицы использовались в Галлии (ныне Франция) и Испании, пока их не вытеснили таблицы Дионисия в конце VIII века.
Таблицы Дионисия и Виктория противоречили тем, которые традиционно использовались на Британских островах. Британские таблицы использовали 84-летний цикл, но ошибка привела к тому, что полнолуния стали наступать все раньше и раньше. [21] Это несоответствие привело к сообщению, что королева Энфледа , по системе Дионисия, постилась в свое Вербное воскресенье, в то время как ее муж Освиу , король Нортумбрии, пировал в свое Пасхальное воскресенье. [22]
В результате ирландского Синода Маг-Лене в 630 году южные ирландцы начали использовать таблицы Дионисия, [23] а северные англичане последовали их примеру после Синода Уитби в 664 году. [24]
Дионисийский счет был полностью описан Бедой в 725 году. [25] Он мог быть принят Карлом Великим для Франкской церкви еще в 782 году от Алкуина , последователя Беды. Дионисийский/Беданский computus использовался в Западной Европе до реформы григорианского календаря и по-прежнему используется в большинстве Восточных церквей, включая подавляющее большинство Восточных православных церквей и нехалкидонских церквей . [26] Единственная Восточная православная церковь, которая не следует этой системе, — это Финская православная церковь, которая использует григорианский.
Отклонившись от александрийцев в VI веке, церкви за восточной границей бывшей Византийской империи, включая Ассирийскую церковь Востока , [27] теперь празднуют Пасху в другие даты, чем Восточные православные церкви, четыре раза каждые 532 года. [ необходима цитата ]
За исключением этих церквей на восточных окраинах Римской империи, к десятому веку все приняли александрийскую Пасху, которая по-прежнему помещала весеннее равноденствие на 21 марта, хотя Беда уже отметил его дрейф в 725 году – он сместился еще дальше к 16 веку. [d] Хуже того, расчетная Луна, которая использовалась для вычисления Пасхи, была привязана к юлианскому году 19-летним циклом. Это приближение создавало ошибку в один день каждые 310 лет, поэтому к 16 веку лунный календарь был не в фазе с реальной Луной на четыре дня. Григорианская Пасха использовалась с 1583 года Римско -католической церковью и была принята большинством протестантских церквей между 1753 и 1845 годами.
Немецкие протестантские государства использовали астрономическую Пасху между 1700 и 1776 годами, основанную на Рудольфовых таблицах Иоганна Кеплера , которые, в свою очередь, основывались на астрономических положениях Солнца и Луны, наблюдавшихся Тихо Браге в его обсерватории Ураниборг на острове Вен , в то время как Швеция использовала ее с 1739 по 1844 год. Эта астрономическая Пасха была воскресеньем после момента полнолуния, который был после момента весеннего равноденствия по времени Ураниборга ( TT + 51 m ) . Однако она задерживалась на одну неделю, если это воскресенье было еврейской датой 15 нисана, первым днем пасхальной недели, рассчитанной в соответствии с современными еврейскими методами. [29]
Это правило 15 нисана повлияло на два шведских года, 1778 и 1798, которые вместо того, чтобы быть на одну неделю раньше григорианской Пасхи, были задержаны на одну неделю, так что они были в то же воскресенье, что и григорианская Пасха. Астрономическая Пасха Германии была на одну неделю раньше григорианской Пасхи в 1724 и 1744 годах. [29] Астрономическая Пасха Швеции была на одну неделю раньше григорианской Пасхи в 1744 году, но на одну неделю позже в 1805, 1811, 1818, 1825 и 1829 годах. [29]
Были предложены две современные астрономические Пасхи, но никогда не использовались ни одной Церковью. Первая была предложена как часть пересмотренного юлианского календаря на Синоде в Константинополе в 1923 году, а вторая была предложена Всемирным советом церквей на консультации 1997 года в Алеппо . Обе использовали то же правило, что и немецкая и шведская версии, но использовали современные астрономические вычисления и иерусалимское время ( TT + 2 ч 21 м ) без правила 15 нисана . Версия 1923 года поместила бы астрономическую Пасху на месяц раньше григорианской Пасхи в 1924, 1943 и 1962 годах, но на неделю позже в 1927, 1954 и 1967 годах. [30] Версия 1997 года поместила бы астрономическую Пасху в то же воскресенье, что и григорианская Пасха на 2000–2025 годы, за исключением 2019 года, когда это было бы на месяц раньше. [31]
Пасхальный цикл группирует дни в лунные месяцы, которые длятся либо 29, либо 30 дней. Есть исключение. Месяц, заканчивающийся в марте, обычно имеет 30 дней, но если 29 февраля високосного года попадает на него, он содержит 31. Поскольку эти группы основаны на лунном цикле , в долгосрочной перспективе средний месяц в лунном календаре является очень хорошим приближением синодического месяца , который29.530 59 дней в длину. [32]
В лунном году 12 синодических месяцев, в общей сложности 354 или 355 дней. Лунный год примерно на 11 дней короче календарного года, который длится 365 или 366 дней. Эти дни, на которые солнечный год превышает лунный, называются эпактами ( ‹См. Tfd› греч . ἐπακταὶ ἡμέραι , транслит. épaktai hēmérai , букв. «вставные дни»). [33] [34]
Необходимо добавить их к дню солнечного года, чтобы получить правильный день в лунном году. Всякий раз, когда эпакта достигает или превышает 30, в лунный календарь необходимо вставить дополнительный вставной месяц (или эмболисмический месяц) из 30 дней: затем 30 необходимо вычесть из эпакты. Чарльз Уитли приводит подробности:
«Таким образом, начиная год с марта (ибо таков был древний обычай), они отводили тридцать дней для луны, [заканчивающейся] в марте, и двадцать девять для той, [заканчивающейся] в апреле; и еще тридцать для мая, и двадцать девять для июня и т. д. согласно древним стихам:
Impar luna pari, par fiet in impare mense;
In quo completur mensi lunatio detur.«Ибо первый, третий, пятый, седьмой, девятый и одиннадцатый месяцы, которые называются impares menses , или неравные месяцы, имеют свои луны согласно исчислению в тридцать дней каждый, которые поэтому называются pares lunae , или равные луны; но второй, четвертый, шестой, восьмой, десятый и двенадцатый месяцы, которые называются pares menses , или равные месяцы, имеют свои луны только в двадцать девять дней каждый, которые называются impares lunae , или неравные луны».
— Уитли 1871, стр. 44
Таким образом, лунный месяц взял название юлианского месяца, в котором он закончился. Девятнадцатилетний метонов цикл предполагает, что 19 тропических лет такие же длинные, как 235 синодических месяцев. Таким образом, через 19 лет лунации должны выпадать таким же образом в солнечных годах, и эпакты должны повторяться. За 19 лет эпакта увеличивается на 19 × 11 = 209 ≡ 29 ( mod 30) , а не на 0 (mod 30) . То есть, 209, деленное на 30, дает остаток 29 вместо того, чтобы быть кратным 30. Это проблема, если компенсация выполняется только путем добавления месяцев по 30 дней. [e] Таким образом, через 19 лет эпакта должна быть скорректирована на один день, чтобы цикл повторился. Это так называемый saltus lunae («скачок луны»). Юлианский календарь справляется с этим, сокращая длину лунного месяца, который начинается 1 июля в последний год цикла, до 29 дней. Это делает три последовательных месяца по 29 дней. [f]
Сальтус и семь дополнительных 30-дневных месяцев были в значительной степени скрыты, поскольку располагались в точках, где юлианские и лунные месяцы начинались примерно в одно и то же время. Дополнительные месяцы начинались 1 января (год 3), 2 сентября (год 5), 6 марта (год 8), 3 января (год 11), 31 декабря (год 13), 1 сентября (год 16) и 5 марта (год 19). [ 35] [36] Порядковый номер года в 19-летнем цикле называется « золотым числом » и определяется по формуле
То есть год номер Y в христианской эре делится на 19, а остаток плюс 1 является золотым числом. (В некоторых источниках указывается, что вы добавляете 1 перед тем, как взять остаток; в этом случае вам нужно рассматривать результат 0 как золотое число 19. В приведенной выше формуле мы сначала берем остаток, а затем добавляем 1, поэтому такая корректировка не требуется.) [g]
Циклы из 19 лет не все имеют одинаковую длину, потому что они могут иметь четыре или пять високосных лет. Но период из четырех циклов, 76 лет ( каллиппический цикл ), имеет длину 76 × 365 + 19 = 27 759 дней (если он не пересекает столетие). В этом периоде 235 × 4 = 940 лунных месяцев, поэтому средняя длина составляет 27 759 / 940 или около 29,530851 дня. Существует 76 × 6 = 456 обычных номинальных 30-дневных лунных месяцев и такое же количество обычных номинальных 29-дневных месяцев, но 19 из них удлиняются на день в високосные дни, плюс 24 вставных месяца по 30 дней и четыре вставных месяца по 29 дней. Поскольку это больше истинной продолжительности синодического месяца, около 29,53059 дней, расчетное пасхальное полнолуние становится все более поздним по сравнению с астрономическим полнолунием, если не вносить поправку, как в григорианской системе (см. ниже).
Пасхальный месяц — первый месяц в году, четырнадцатый день которого (формальное полнолуние ) приходится на 21 марта или после него. Пасха — это воскресенье после 14-го дня (или, говоря то же самое, воскресенье в пределах третьей недели). Пасхальный лунный месяц всегда начинается с даты в 29-дневном периоде с 8 марта по 5 апреля включительно. Его четырнадцатый день, таким образом, всегда приходится на дату между 21 марта и 18 апреля включительно (в григорианском или юлианском календаре, для западной и восточной системы соответственно), а следующее воскресенье тогда обязательно приходится на дату в диапазоне от 22 марта до 25 апреля включительно. Однако в западной системе Пасха не может приходиться на 22 марта в течение 300-летнего периода 1900–2199 (см. ниже). В солнечном календаре Пасха называется подвижным праздником , поскольку ее дата колеблется в пределах 35 дней. Однако в лунном календаре Пасха всегда приходится на третье воскресенье пасхального лунного месяца и не более «перемещаема», чем любой праздник, привязанный к определенному дню недели и неделе в пределах месяца, например, День благодарения .
Поскольку реформирование computus было основной мотивацией для введения григорианского календаря в 1582 году, соответствующая методология computus была введена вместе с новым календарем. [h] Общий метод работы был дан Клавием в Шести Канонах (1582), а полное объяснение последовало в его Explicatio (1603). [37]
Пасхальное воскресенье — это воскресенье, следующее за датой пасхального полнолуния. Дата пасхального полнолуния — это церковная дата полнолуния 21 марта или позже. Григорианский метод выводит даты пасхального полнолуния путем определения эпакты для каждого года. [38] Эпакта может иметь значение от * (0 или 30) до 29 дней. Это возраст Луны в днях (т. е. лунная дата) на 1 января, уменьшенный на один день. В своей книге The Easter computus and the origins of the Christian era Олден А. Мосхаммер неверно [ по мнению кого? ] утверждает: «Теоретически эпакта 30 = 0 представляет новолуние в его соединении с солнцем. Эпакта 1 представляет теоретическую первую видимость первого полумесяца Луны. Именно с этой точки как с первого дня отсчитывается четырнадцатый день Луны». [39]
Четырнадцатый день лунного месяца считается днем полнолуния . [ 40] Это день лунного месяца, на который с наибольшей вероятностью приходится момент противостояния («полнолуние»). «Новолуние» с наибольшей вероятностью станет видимым (как тонкий полумесяц на западном небе после захода Солнца) в первый день лунного месяца. Соединение солнца и луны («новолуние») с наибольшей вероятностью приходится на предыдущий день, который является 29-м днем «пустого» (29-дневного) месяца и 30-м днем «полного» (30-дневного) месяца.
Исторически дата пасхального полнолуния для года определялась по ее порядковому номеру в метоновом цикле, называемом золотым числом , который повторяет лунную фазу 1 января каждые 19 лет. [41] Этот метод был изменен в григорианской реформе, поскольку табличные даты перестают соответствовать действительности примерно через два столетия, но с помощью метода эпакта можно построить упрощенную таблицу, которая имеет срок действия от одного до трех столетий. [42] [43]
Эпакты текущего метонова цикла, начавшегося в 2014 году, следующие:
Как можно видеть, дата пасхального полнолуния в определенном году обычно либо на 11 дней раньше, чем в предыдущем году, либо на 19 дней позже. Исключениями являются годы 1, 6 и 17 цикла, когда дата всего на 18 дней позже, а в годы 7 и 18 всего на 10 дней раньше, чем в предыдущем году. В восточной системе (см. ниже) пасхальное полнолуние обычно наступает на четыре дня позже. Оно наступает на 34 дня позже в пяти из 19 лет и на 5 дней позже в годах 6 и 17, потому что в эти годы григорианская система помещает пасхальное полнолуние на день раньше, чем обычно, чтобы соблюсти Пасху до 26 апреля, как объясняется ниже. В 2100 году нашей эры разница увеличится на один день.
Эпаксы используются для нахождения дат новолуния следующим образом: запишите таблицу всех 365 дней года (високосный день игнорируется). Затем обозначьте все даты римской цифрой, считая по убыванию, от "*" (0 или 30), "xxix" (29), до "i" (1), начиная с 1 января, и повторяйте это до конца года. Однако в каждом втором таком периоде отсчитывайте только 29 дней и обозначьте дату как xxv (25), а также как xxiv (24). Поэтому считайте 13-й период (последние одиннадцать дней) длинным и присвойте метки "xxv" и "xxiv" последовательным датам (26 и 27 декабря соответственно). [45]
Добавьте метку "25" к датам, которые имеют "xxv" в 30-дневных периодах; но в 29-дневных периодах (которые имеют "xxiv" вместе с "xxv") добавьте метку "25" к дате с "xxvi". Распределение продолжительности месяцев и продолжительности циклов эпакта таково, что каждый гражданский календарный месяц начинается и заканчивается одной и той же меткой эпакта, за исключением февраля и, можно сказать, августа, который начинается с двойной метки "xxv"/"xxiv", но заканчивается одинарной меткой "xxiv". Эта таблица называется calendarium . Церковные новолуния для любого года - это те даты, когда вводится эпакта для года. [45]
Если эпакта для года, например, 27, то есть церковное новолуние на каждую дату в этом году, которая имеет метку эпакты "xxvii" (27). Если эпакта 25, то есть усложнение, введенное для того, чтобы церковное новолуние не попадало на одну и ту же дату дважды в течение метонова цикла. Если действующий цикл эпакты включает эпакту 24 (как это делает цикл, используемый с 1900 года и до 2199 года), то эпакта 25 помещает церковное новолуние на 4 апреля (имея метку "25"), в противном случае это 5 апреля (имея метку "xxv"). [45]
Эпакта 25, дающая 4 апреля, может произойти только в том случае, если золотое число больше 11. В этом случае это будет 11 лет спустя после года с эпактой 24. Так, например, в 1954 году золотое число было 17, эпакта была 25, церковное новолуние считалось 4 апреля, полнолуние — 17 апреля. Пасха была 18 апреля, а не 25 апреля, как это было бы в противном случае, например, в 1886 году, когда золотое число было 6. Эта система автоматически вставляет семь месяцев в метонов цикл.
Обозначьте все даты в таблице буквами от «A» до «G», начиная с 1 января, и повторяйте до конца года. Если, например, первое воскресенье года приходится на 5 января, в котором есть буква «E», то каждая дата с буквой «E» является воскресеньем в этом году. Тогда «E» называется доминиканской буквой для этого года — от dies dominica (лат. «день Господень»). Доминиканская буква циклически возвращается на одну позицию назад каждый год. В високосные годы после 24 февраля воскресенья приходятся на предыдущую букву цикла, поэтому високосные годы имеют две доминиканские буквы: первая для дня до, вторая для дня после високосного.
На практике, для расчета Пасхи, это не нужно делать для всех 365 дней года. Для эпактов март выходит точно таким же, как январь, поэтому не нужно рассчитывать январь или февраль. Чтобы избежать необходимости рассчитывать Dominical Letters для января и февраля, начните с D для 1 марта. Вам нужны эпакты только с 8 марта по 5 апреля. Это приводит к следующей таблице:

Например, если эпакта 27 (xxvii), церковное новолуние приходится на каждую дату, обозначенную как xxvii . Церковное полнолуние приходится на 13 дней позже. Из таблицы выше это дает новолуние 4 марта и 3 апреля, а также полнолуние 17 марта и 16 апреля. Тогда Пасха — это первое воскресенье после первого церковного полнолуния 21 марта или после этой даты. (В этом определении используется «21 марта или после этой даты», чтобы избежать двусмысленности с историческим значением слова «после». В современном языке эта фраза просто означает «после 20 марта». Определение «21 марта или после этой даты» часто неправильно сокращается до «после 21 марта» в опубликованных и веб-статьях, что приводит к неправильным датам Пасхи.) В этом примере это пасхальное полнолуние приходится на 16 апреля. Если господствующая буква — E, то Пасха приходится на 20 апреля.
Метка « 25 » (в отличие от «xxv») используется следующим образом: в пределах метонова цикла годы, отстоящие друг от друга на 11 лет, имеют эпакты, отличающиеся на один день. Месяц, начинающийся с даты с метками xxiv и xxv, написанными рядом, имеет либо 29, либо 30 дней. Если эпакты 24 и 25 происходят в пределах одного метонова цикла, то новолуния (и полнолуния) будут приходиться на одни и те же даты для этих двух лет. Это возможно для реальной луны [j], но неэлегантно в схематическом лунном календаре; даты должны повторяться только через 19 лет. Чтобы избежать этого, в годы с эпактами 25 и с золотым числом больше 11, вычисляемое новолуние приходится на дату с меткой 25, а не xxv . Там, где метки 25 и xxv находятся вместе, проблем не возникает, поскольку они одинаковы. Это не переносит проблему на пару «25» и «xxvi», поскольку самая ранняя эпакта 26 могла появиться в 23-м году цикла, который длится всего 19 лет: между ними происходит скачок Луны , из-за которого новолуния приходятся на разные даты.
Григорианский календарь имеет поправку к тропическому году, отбрасывая три високосных дня за 400 лет (всегда в столетнем году). Это поправка к длине тропического года, но она не должна влиять на метоновское отношение между годами и лунациями. Поэтому эпакта компенсируется (частично – см. эпакта ) вычитанием одного в этих столетии. Это так называемая солнечная поправка или «солнечное уравнение» («уравнение» используется в средневековом смысле «поправки»).
Однако 19 неисправленных юлианских лет немного длиннее 235 лунаций. Разница накапливается до одного дня примерно за 308 лет, или 0,00324 дня в году. За один цикл эпакта уменьшается из-за солнечной коррекции в среднем на 19 × 0,0075 = 0,1425, поэтому цикл эквивалентен 235−0,1425/30 = 234,99525 месяцам, тогда как на самом деле существует 19 × 365,2425 / 29,5305889 ≈ 234,997261 синодических месяцев. Разница в 0,002011 синодических месяцев за 19-летний цикл, или 0,003126 дня в году, требует периодической лунной коррекции эпакты. В григорианском календаре это делается путем добавления 1 восемь раз за 2500 (григорианских) лет (немного больше, чем 2500 × 0,003126, или около 7,8), всегда в столетнем году: это так называемая лунная коррекция (исторически называемая «лунное уравнение»). Первая была применена в 1800 году, следующая — в 2100 году, и будет применяться каждые 300 лет, за исключением интервала в 400 лет между 3900 и 4300 годами, который начинает новый цикл. Во время реформы эпакты были изменены на 7, хотя 10 дней были пропущены, чтобы внести трехдневную коррекцию в определение времени новолуний. [45]
Солнечные и лунные поправки работают в противоположных направлениях, и в некоторые столетние годы (например, 1800 и 2100) они отменяют друг друга. В результате григорианский лунный календарь использует таблицу эпакты, которая действительна в течение периода от 100 до 300 лет. Приведенная выше таблица эпакты действительна в течение периода с 1900 по 2199 год.
Как объясняется ниже, даты Пасхи повторяются через 5 700 000 лет, и за этот период средняя продолжительность церковного месяца составляет 2 081 882 250/70 499 183 ≈ 29,5305869 дней, [46] что отличается от текущей фактической средней продолжительности лунации (29,5305889 d: см. Лунный месяц#Синодический месяц ) на 6-ю цифру после запятой. Это соответствует ошибке менее суток в фазе Луны за 40 000 лет, но на самом деле продолжительность суток меняется (как и продолжительность синодического месяца), поэтому система не точна за такие периоды. См. статью ΔT (хронометраж) для получения информации о кумулятивном изменении продолжительности суток.
Этот метод расчета имеет несколько тонкостей:
Каждый второй лунный месяц имеет только 29 дней, поэтому один день должен иметь два (из 30) назначенных ему эпакта. Причина перемещения эпакта "xxv/25", а не любого другого, по-видимому, следующая: Согласно Дионисию (в его вступительном письме к Петронию), Никейский собор, на основании авторитета Евсевия , установил, что первый месяц церковного лунного года (пасхальный месяц) должен начинаться между 8 марта и 5 апреля включительно, а 14-й день приходится на период между 21 марта и 18 апреля включительно, таким образом охватывая период (всего) в 29 дней. Новолуние 7 марта, имеющее эпакта "xxiv", имеет свой 14-й день (полнолуние) 20 марта, что слишком рано (не следует за 20 марта). Таким образом, годы с эпактой "xxiv", если лунный месяц, начинающийся 7 марта, имел 30 дней, имели бы пасхальное новолуние 6 апреля, что слишком поздно: полнолуние пришлось бы на 19 апреля, а Пасха могла бы быть уже 26 апреля. В юлианском календаре самая поздняя дата Пасхи была 25 апреля, и григорианская реформа сохранила этот предел. Таким образом, пасхальное полнолуние должно приходиться не позднее 18 апреля, а новолуние - на 5 апреля, что имеет метку эпакты "xxv". Следовательно, 5 апреля должно иметь свои двойные метки эпакты "xxiv" и "xxv". Тогда эпакта "xxv" должна обрабатываться по-другому, как объяснено в параграфе выше.
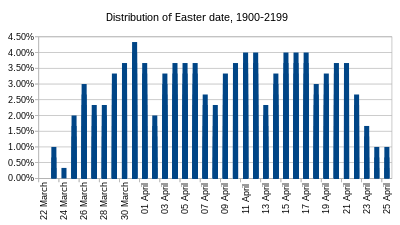
Распределение частот для даты Пасхи определено неточно, потому что каждые 100–300 лет отображение от золотого числа к эпакту меняется, а долгосрочное распределение частот действительно только в течение миллионов лет (см. ниже), тогда как система, безусловно, не будет использоваться так долго. Текущее отображение, действительное с 1900 по 2199 год, дает даты Пасхи с сильно различающимися частотами. 22 марта никогда не может произойти, тогда как 31 марта происходит 13 раз за этот 300-летний период.
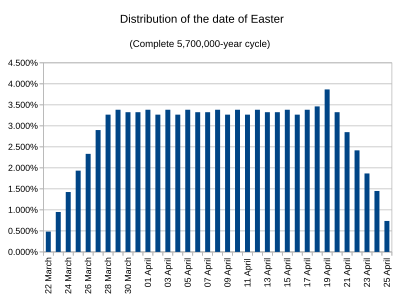
Если задаться вопросом, каким будет распределение в долгосрочной перспективе, то есть в течение всего периода в 5,7 миллионов лет, после которого даты повторяются, то это распределение можно найти довольно просто, и оно сильно отличается от распределения в период с 1900 по 2199 год или даже от распределения в период с момента реформы до настоящего времени. Дата Пасхи в данном году зависит только от эпакта для года, его золотого числа и его господской буквы , которая сообщает нам, какие дни являются воскресеньями (точнее, господской буквы для части года после февраля, которая в високосные годы отличается от буквы для января и февраля). (Золотое число имеет значение только тогда, когда эпакта равна 25, как объяснялось ранее.) Если мы перейдем на 3 230 000 лет вперед от определенного года, мы найдем год в той же точке 400-летнего григорианского цикла и с тем же золотым числом, но с эпактой, увеличенной на 1. Поэтому в долгосрочной перспективе все тридцать эпакт одинаково вероятны. С другой стороны, не все доминиональные буквы имеют одинаковую частоту — годы с буквами A и C (в конце года) встречаются в 14% случаев каждая, E и F встречаются в 14,25% случаев, а B, D и G встречаются в 14,5% случаев. Принимая во внимание усложнение, связанное с эпактой 25, это дает распределение, показанное на втором графике. 19 апреля является наиболее распространенным, потому что когда эпакта равна 25, церковное полнолуние выпадает на 17 или 18 апреля (в зависимости от золотого числа), и оно также выпадает на эти даты, когда эпакта равна 26 или 24 соответственно. Есть семь дней, на которые может выпасть полнолуние, включая 17 и 18 апреля, для того, чтобы Пасха была 19 апреля (это также самая поздняя возможная дата Пасхи, когда церковное полнолуние может выпасть на субботу, так как 18 апреля является самой поздняя дата церковного полнолуния, которое наступает на следующий день, если церковное полнолуние приходится на субботу). [45] Как следствие, 19 апреля является датой, на которую Пасха выпадает чаще всего в григорианском календаре, примерно в 3,87% лет. 22 марта является наименее частой датой, с 0,48%. [47] [45]
Связь между лунными и солнечными календарными датами делается независимой от схемы високосных дней для солнечного года. В основном григорианский календарь по-прежнему использует юлианский календарь с високосным днем каждые четыре года, поэтому метонов цикл из 19 лет имеет 6940 или 6939 дней с пятью или четырьмя високосными днями. Теперь лунный цикл насчитывает только 19 × 354 + 19 × 11 = 6935 дней . Не маркируя и не подсчитывая високосный день с помощью числа эпакта, но имея следующее новолуние, приходящееся на ту же календарную дату, что и без високосного дня, текущая лунация удлиняется на день, [k] и 235 лунаций охватывают столько же дней, сколько и 19 лет (при условии, что 19 лет не включают «солнечную коррекцию», как в 1900 году). Таким образом, бремя синхронизации календаря с луной (промежуточная точность) перекладывается на солнечный календарь, который может использовать любую подходящую схему интеркаляции, все при условии, что 19 солнечных лет = 235 лунаций (что создает долгосрочную неточность, если не исправить ее «лунной коррекцией»). Следствием этого является то, что вычисленный возраст луны может быть смещен на один день, а также то, что лунации, содержащие високосный день, могут быть 31 день, чего никогда бы не произошло, если бы следовали реальной луне (краткосрочные неточности). Такова цена регулярной подгонки под солнечный календарь.
С точки зрения тех, кто хотел бы использовать григорианский пасхальный цикл в качестве календаря на весь год, в григорианском лунном календаре [48] есть некоторые недостатки (хотя они не влияют на пасхальный месяц и дату Пасхи):
Тщательный анализ показывает, что, судя по тому, как они используются и корректируются в григорианском календаре, эпакты на самом деле 1/30 лунации и не полных дней. См. epact для обсуждения.
Солнечные и лунные поправки повторяются через 4 × 25 = 100 столетий. За этот период эпакта для данного золотого числа изменяется в общей сложности на −1 × 3/4 × 100 + 1 × 8/25 × 100 = −43 ≡ 17 mod 30 . Это простое число для 30 возможных эпактов, поэтому требуется 100 × 30 = 3000 столетий , прежде чем отображения эпактов повторятся; и 3000 × 19 = 57000 столетий, прежде чем они повторятся с тем же золотым числом. Неочевидно, сколько церковных Новолуний подсчитано в этом периоде в 5,7 млн лет. Метонические циклы составляют в сумме (5 700 000/19) × 235 = 70 500 000 лунаций. Но есть чистые −43 × (5 700 000/10 000) поправок к эпактам, которые при делении на 30 дают поправку −817 лунаций, что в сумме составляет 70 499 183 лунаций. Это число, по-видимому, впервые вывел Магнус Георг Паукер в 1837 году. [49] Оно также упоминается в главе о календарях (стр. 744) в Морском альманахе 1931 года [50] и в Пояснительном дополнении 1992 года (стр. 582). [51] [l] Таким образом, даты Григорианской Пасхи повторяются в точно таком же порядке только через 5 700 000 лет, 70 499 183 лунаций или 2 081 882 250 дней; средняя длина лунного месяца тогда составляет 2 081 882 250/70 499 183 = 29,53058690 дней. Конечно, календарь должен быть скорректирован через несколько тысячелетий из-за изменений в длине тропического года, синодического месяца и дня.

Это поднимает вопрос, почему григорианский лунный календарь имеет отдельные солнечные и лунные поправки, которые иногда отменяют друг друга. Оригинальная работа Лилиуса не сохранилась, но его предложение было описано в Compendium Novae Rationis Restituendi Kalendarium, распространенном в 1577 году, в котором объясняется, что разработанная им система исправлений должна была стать совершенно гибким инструментом в руках будущих реформаторов календаря, поскольку солнечный и лунный календари отныне могли быть исправлены без взаимного вмешательства. [52] Примером такой гибкости была альтернативная последовательность интеркаляции, полученная из теорий Коперника, вместе с соответствующими ей эпактными поправками. [53]
«Солнечные поправки» приблизительно отменяют эффект григорианских изменений високосных дней солнечного календаря на лунный календарь: они (частично) возвращают цикл эпакты к изначальному метоновскому соотношению между юлианским годом и лунным месяцем. Присущее несоответствие между солнцем и луной в этом базовом 19-летнем цикле затем исправляется каждые три или четыре столетия «лунной коррекцией» эпакты. Однако поправки эпакты происходят в начале григорианских столетий, а не юлианских, и поэтому исходный юлианский метоновский цикл не восстанавливается полностью.
В то время как чистые 4 × 8 − 3 × 25 = 43 вычитания эпактов можно было бы равномерно распределить на 10 000 лет (как было предложено, например, Лихтенбергом 2003, стр. 45–76), если поправки объединить, то неточности двух циклов также будут добавлены и не могут быть исправлены по отдельности.
Соотношения (средних солнечных) дней в году и дней в лунный месяц изменяются как из-за внутренних долгосрочных изменений орбит, так и из-за замедления вращения Земли из-за приливного торможения , поэтому григорианские параметры становятся все более устаревшими.
Это влияет на дату равноденствия, но так уж получилось, что интервал между равноденствиями на севере (весна в северном полушарии) был довольно стабильным на протяжении исторических времен, особенно если измерять его по среднему солнечному времени. [54] [55]
Кроме того, смещение церковных полнолуний, рассчитанных по григорианскому методу, по сравнению с истинными полнолуниями затронуто меньше, чем можно было бы ожидать, поскольку увеличение продолжительности дня почти точно компенсируется увеличением продолжительности месяца, поскольку приливное торможение преобразует угловой момент вращения Земли в орбитальный угловой момент Луны.
Птолемеевское значение продолжительности среднего синодического месяца, установленное около IV в. до н. э. вавилонянами, составляет 29 дней 12 ч. 44 мин. 3+1/3 с (см. Кидинну ); текущее значение на 0,46 с меньше (см. Новолуние ). За тот же исторический отрезок времени продолжительность среднего тропического года уменьшилась примерно на 10 с (все значения означают солнечное время).
Часть раздела табличных методов выше описывает исторические аргументы и методы, с помощью которых современные даты Пасхального воскресенья были определены в конце XVI века Католической церковью. В Британии, где тогда все еще использовался юлианский календарь, Пасхальное воскресенье определялось с 1662 по 1752 год (в соответствии с предыдущей практикой) простой таблицей дат в Англиканской Книге общих молитв (установленной Актом о единообразии 1662 года ). Таблица была индексирована непосредственно золотым числом и буквой воскресенья , которые (в пасхальном разделе книги) предположительно были уже известны.
Для Британской империи и колоний новое определение даты Пасхального воскресенья было определено тем, что сейчас называется Актом о календаре (Новый стиль) 1750 года с приложением. Метод был выбран для указания дат, согласующихся с григорианским правилом, уже используемым в других местах. Акт требовал, чтобы он был помещен в Книгу общих молитв , и, следовательно, это общее англиканское правило. Первоначальный акт можно увидеть в British Statutes at Large 1765. [ 56] Приложение к акту включает определение: « Пасхальный день (от которого зависят остальные) всегда является первым воскресеньем после Полнолуния , которое происходит в двадцать первый день марта или следующим за ним . И если Полнолуние происходит в воскресенье , Пасхальный день является следующим воскресеньем ». В приложении впоследствии используются термины «Пасхальное полнолуние» и «Церковное полнолуние», что дает понять, что они приближаются к реальному полнолунию.
Метод совершенно отличается от описанного выше в § Григорианская реформа computus. Для общего года сначала определяется золотое число , затем используются три таблицы для определения воскресной буквы , «шифра» и даты пасхального полнолуния, из которой следует дата пасхального воскресенья. Эпакта явно не появляется. Более простые таблицы могут использоваться для ограниченных периодов (например, 1900–2199), в течение которых шифр (который представляет эффект солнечных и лунных поправок) не меняется. Детали Клавия были использованы при построении метода, но они не играют никакой последующей роли в его использовании. [57] [58]
Дж. Р. Стоктон показывает свой вывод эффективного компьютерного алгоритма, прослеживаемого к таблицам в молитвеннике и Календарном акте (предполагая, что описание того, как использовать Таблицы, имеется под рукой), и проверяет его процессы путем вычисления соответствующих таблиц. [59]

Метод вычисления даты церковного полнолуния, который был стандартным для западной церкви до реформы григорианского календаря и до сих пор используется большинством восточных христиан , использовал неисправленное повторение 19-летнего метонова цикла в сочетании с юлианским календарем. С точки зрения метода эпактов, обсуждавшегося выше, он фактически использовал единую таблицу эпактов, начинающуюся с эпакта 0, который никогда не корректировался. В этом случае эпакт отсчитывался от 22 марта, самой ранней приемлемой даты для Пасхи. Это повторяется каждые 19 лет, поэтому существует только 19 возможных дат для пасхального полнолуния с 21 марта по 18 апреля включительно.
Поскольку нет никаких поправок, как в григорианском календаре, церковное полнолуние отдаляется от истинного полнолуния более чем на три дня каждое тысячелетие. Оно уже на несколько дней позже. В результате восточные церкви празднуют Пасху на одну неделю позже западных церквей примерно в 44% случаев и в тот же день примерно в 30% случаев. (Восточная Пасха иногда на четыре или пять недель позже, потому что юлианский календарь отстает от григорианского на 13 дней в 1900–2099 годах, и поэтому григорианское пасхальное полнолуние иногда бывает раньше юлианского 21 марта.)
Порядковый номер года в 19-летнем цикле называется его золотым числом . Этот термин впервые был использован в компьютерной поэме Massa Compoti Александра де Вилья Деи в 1200 году. Более поздний писец добавил золотое число в таблицы, первоначально составленные Аббо из Флери в 988 году.
Утверждение Католической церкви в папской булле 1582 года Inter gravissimas , которая обнародовала григорианский календарь, о том, что она восстанавливает «празднование Пасхи в соответствии с правилами, установленными... великим вселенским собором в Никее» [60], основывалось на ложном утверждении Дионисия Малого (525) о том, что «мы определяем дату Пасхи... в соответствии с предложением, согласованным 318 Отцами Церкви на соборе в Никее» [61] .
Однако Первый Никейский собор (325 г.) не установил никаких четких правил для определения этой даты, а лишь написал: «Все наши братья на Востоке, которые прежде следовали обычаю иудеев, должны отныне праздновать упомянутый священнейший праздник Пасхи в одно и то же время с римлянами и вами [Александрийской церковью] и всеми теми, кто соблюдал Пасху с самого начала». [62] Средневековый компутус был основан на александрийском компутусе , который был разработан Александрийской церковью в первом десятилетии IV века с использованием александрийского календаря . [63]
Восточная Римская империя приняла его вскоре после 380 года после перевода computus на юлианский календарь. [64] Рим принял его где-то между шестым и девятым веками. Британские острова приняли его в восьмом веке, за исключением нескольких монастырей. [ нужна цитата ] Франкия (вся Западная Европа, кроме Скандинавии (языческой), Британских островов, Пиренейского полуострова и южной Италии) приняла его в последней четверти восьмого века. [ нужна цитата ]
Последний кельтский монастырь, принявший его, Иона , сделал это в 716 году. [ необходима цитата ] Последний английский монастырь, принявший его, сделал это в 931 году. [ необходима цитата ] До этого другие методы выдавали даты пасхального воскресенья, которые могли отличаться на пять недель. [ необходима цитата ]
Ниже представлена таблица дат пасхальных полнолуний для всех юлианских лет с 931 года:
Как упоминалось ранее, эти пасхальные полнолуния наступают на 4, 5 или 34 дня позже, чем в западной системе, и примерно на три дня позже астрономического полнолуния. (Например, лунное затмение в апреле 2015 года произошло 4 апреля по григорианскому календарю или 22 марта по юлианскому календарю, но пасхальное полнолуние в том году (золотое число 2) было 25 марта по юлианскому календарю.) Всякий раз, когда происходит лунная коррекция, разница между западными и восточными церковными полнолуниями увеличивается на 1, поэтому с 2100 по 2399 год разница составит 5, 6 или 35 дней. Диапазон дат в григорианском календаре восточного пасхального полнолуния смещается на один день позже каждый раз, когда происходит солнечная коррекция, поэтому с 2100 по 2199 год это будет с 5 апреля по 9 мая. В настоящее время существует пять лет в цикле, когда Восточная Пасха на несколько недель позже Западной, в золотые числа 3, 8, 11, 14 и 19. Это увеличится до шести раз за цикл в 2200 году (добавление золотого числа 6), до семи в 2300 году (добавление золотого числа 17), затем снова до шести в 2400 году (лунная коррекция и отсутствие солнечной коррекции), снова до семи в 2500 году и до восьми только в 2900 году (добавление золотого числа 9). [ необходима цитата ]
Пример расчета с использованием этой таблицы:
Золотое число для 1573 года — 16 ( 1573 + 1 = 1574 ; 1574 ÷ 19 = 82 остаток 16 ). Из таблицы пасхальное полнолуние для золотого числа 16 — 21 марта. Из таблицы недель 21 марта — суббота. Пасхальное воскресенье — следующее воскресенье, 22 марта.
Итак, для данной даты церковного полнолуния существует семь возможных дат Пасхи. Цикл воскресных писем не повторяется через семь лет: из-за перерывов в виде високосного дня каждые четыре года полный цикл, в котором будние дни повторяются в календаре одинаково, составляет 4 × 7 = 28 лет, солнечный цикл . Таким образом, даты Пасхи повторяются в том же порядке через 4 × 7 × 19 = 532 года. Этот пасхальный цикл также называется викторианским циклом , в честь Виктория Аквитанского, который ввел его в Риме в 457 году.
Известно, что впервые его использовал Анниан Александрийский в начале V века. Иногда его также ошибочно называли дионисийским циклом , в честь Дионисия Малого , который подготовил пасхальные таблицы, начавшиеся в 532 году. Он, по-видимому, не осознавал, что описанный им александрийский computus имел 532-летний цикл, хотя он осознавал, что его 95-летняя таблица не была истинным циклом. Достопочтенный Беда (VII век), по-видимому, был первым, кто определил солнечный цикл и объяснил пасхальный цикл из метонова цикла и солнечного цикла.
В средневековой Западной Европе приведенные выше даты пасхального полнолуния (14 нисана) можно было запомнить с помощью 19-строчного аллитерационного стихотворения на латыни: [65] [66]
Первая половина каждой строки дает дату пасхального полнолуния из таблицы выше для каждого года в 19-летнем цикле. Вторая половина строки дает регулярный фериал или смещение буднего дня дня пасхального полнолуния этого года от текущего , или буднего дня 24 марта. [67] Регулярный фериал повторяется римскими цифрами в третьем столбце.
Из-за расхождений между приближениями вычислительных расчетов времени среднего ( северного полушария) весеннего равноденствия и лунных фаз и истинными значениями, вычисленными в соответствии с астрономическими принципами, иногда возникают различия между датой Пасхи согласно вычислительным расчетам и гипотетической датой Пасхи, вычисленной астрономическими методами с использованием принципов, приписываемых отцам Церкви. Эти расхождения называются «парадоксальными» датами Пасхи. [68]
В своем Kalendarium 1474 года Региомонтан вычислил точное время всех соединений Солнца и Луны для долготы Нюрнберга согласно таблицам Альфонса за период с 1475 по 1531 год. В своей работе он составил таблицу из 30 случаев, когда Пасха юлианского компутуса не соответствовала Пасхе, вычисленной с использованием астрономического новолуния . В восемнадцати случаях дата отличалась на неделю, в семи случаях на 35 дней и в пяти случаях на 28 дней. [68]
Людвиг Ланге исследовал и классифицировал различные типы парадоксальных дат Пасхи с помощью григорианского компьютуса . [69] В случаях, когда первое весеннее полнолуние согласно астрономическому расчету приходится на воскресенье, а компьютус дает то же воскресенье, что и Пасха, празднуемая Пасха происходит на одну неделю раньше по сравнению с гипотетической «астрономически» правильной Пасхой. Ланге назвал этот случай отрицательным недельным (гебдомадальным) парадоксом (H− парадокс). Если астрономический расчет дает субботу для первого весеннего полнолуния, а Пасха празднуется не в непосредственно следующее воскресенье, а на неделю позже, Пасха празднуется согласно компьютусу на одну неделю позже по сравнению с астрономическим результатом. Он классифицировал такие случаи как положительный недельный (гебдомадальный) парадокс (H+ парадокс). [69]
Расхождения еще больше, если есть разница в соответствии с весенним равноденствием относительно астрономической теории и приближения computus . Если астрономическое равноденственное полнолуние выпадает до вычислительного равноденственного полнолуния, Пасха будет праздноваться на четыре или даже пять недель позже. Такие случаи называются положительным равноденственным парадоксом (парадокс A+) по Ланге. В обратном случае, когда вычислительное равноденственное полнолуние выпадает на месяц раньше астрономического равноденственного полнолуния, Пасха празднуется на четыре или пять недель раньше. Такие случаи называются отрицательным равноденственным парадоксом (парадокс A−). [69]
Парадоксы равноденствия всегда справедливы глобально для всей Земли, потому что последовательность равноденствия и полнолуния не зависит от географической долготы. Напротив, еженедельные парадоксы в большинстве случаев локальны и справедливы только для части Земли, потому что смена дня между субботой и воскресеньем зависит от географической долготы. Вычислительные расчеты основаны на астрономических таблицах, справедливых для долготы Венеции, которую Ланге назвал григорианской долготой. [69]
В 21-м и 22-м веках [69] [70] отрицательные еженедельные парадоксальные даты Пасхи встречаются в 2049, 2076, 2106, 2119 (глобальные), 2133, 2147, 2150, 2170 и 2174 годах. Положительные еженедельные парадоксальные даты встречаются в 2045, 2069, 2089 (глобальные) и 2096 годах. Положительные равноденственные парадоксальные даты в 2019, 2038, 2057, 2076, 2095, 2114, 2133, 2152, 2171 и 2190 годах. [70]
В 2076 и 2133 годах происходят двойные парадоксы (положительный равноденственный и отрицательный недельный). Отрицательные равноденственные парадоксы чрезвычайно редки. Они происходят только дважды до 4000 года в 2353 году, когда Пасха наступает на пять недель раньше, и в 2372 году, когда Пасха наступает на четыре недели раньше. [70]
При выражении пасхальных алгоритмов без использования таблиц принято использовать только целочисленные операции сложение , вычитание , умножение , деление , модуль и присваивание , поскольку это совместимо с использованием простых механических или электронных калькуляторов. Это ограничение нежелательно для компьютерного программирования, где доступны условные операторы и операторы, а также таблицы поиска. Легко увидеть, как можно выполнить преобразование из дня марта (с 22 по 56) в день и месяц (с 22 марта по 25 апреля) как if (DoM > 31) {Day=DoM-31, Month=Apr} else {Day=DoM, Month=Mar}. Что еще более важно, использование таких условных операторов также упрощает ядро григорианского расчета.
В 1800 году математик Карл Фридрих Гаусс представил этот алгоритм для вычисления даты юлианской или григорианской Пасхи. [71] [72] Он исправил выражение для вычисления переменной p в 1816 году. [73] В 1800 году он неправильно заявил, что p = floor ( к/3 ) = ⌊ к/3 ⌋ . В 1807 году он заменил условие (11 M + 11) mod 30 < 19 на более простое a > 10 . В 1811 году он ограничил свой алгоритм только 18-м и 19-м веками и заявил, что 26 апреля всегда заменяется на 19, а 25 апреля на 18 апреля в указанных обстоятельствах. В 1816 году он поблагодарил своего ученика Питера Пауля Титтеля за то, что тот указал на то, что p было неправильным в первоначальной версии. [74]
Анализ алгоритма Пасхи Гаусса разделен на две части. Первая часть — приблизительное отслеживание лунной орбиты, а вторая часть — точное детерминированное смещение для получения воскресенья, следующего за полнолунием.
Первая часть состоит из определения переменной d , количества дней (считая с 22 марта) до дня после полнолуния. Формула для d содержит члены 19 a и константу M . a — это положение года в 19-летнем цикле лунных фаз, в котором, по предположению, движение Луны относительно Земли повторяется каждые 19 календарных лет. В прежние времена 19 календарных лет приравнивались к 235 лунным месяцам (цикл Метона), что удивительно близко, поскольку 235 лунных месяцев составляют приблизительно 6939,6813 дней, а 19 лет в среднем составляют 6939,6075 дней.
Выражение (19 a + M ) mod 30 повторяется каждые 19 лет в каждом столетии, поскольку M определяется на столетие. 19-летний цикл не имеет ничего общего с «19» в 19 a ; это просто совпадение, что появляется еще одно «19». «19» в 19 a возникает из-за исправления несоответствия между календарным годом и целым числом лунных месяцев.
Календарный год (невисокосный) состоит из 365 дней, и ближайший год, который может быть с целым числом лунных месяцев, составляет 12 × 29,5 = 354 дня. Разница составляет 11 дней, что необходимо исправить, сдвинув полнолуние следующего года на 11 дней назад. Но в арифметике по модулю 30 вычитание 11 равносильно добавлению 19, следовательно, прибавление 19 для каждого добавленного года, т. е. 19 a .
M в 19 a + M служит для того, чтобы иметь правильную начальную точку в начале каждого столетия. Она определяется расчетом, в котором учитывается количество високосных лет до этого столетия, где k запрещает високосный день каждые 100 лет, а q переустанавливает его каждые 400 лет, что дает ( k − q ) как общее количество запретов на шаблон високосного дня каждые четыре года. Таким образом, мы добавляем ( k − q ) для коррекции високосных дней, которые никогда не случались. p корректирует лунную орбиту, которая не может быть полностью описана в целочисленных терминах.
Диапазон дней, рассматриваемых для полнолуния, чтобы определить Пасху, составляет от 21 марта (день церковного весеннего равноденствия) до 18 апреля — 29-дневный диапазон. Однако в арифметике mod 30 переменной d и константы M , обе из которых могут иметь целые значения в диапазоне от 0 до 29, диапазон составляет 30. Поэтому в критических случаях вносятся корректировки. После определения d это число дней, которое нужно прибавить к 22 марта (день после самого раннего возможного полнолуния, которое совпадает с церковным весенним равноденствием), чтобы получить дату дня после полнолуния.
Таким образом, первая допустимая дата Пасхи — 22 марта + d + 0 , поскольку Пасха отмечается в воскресенье после церковного полнолуния; то есть, если полнолуние приходится на воскресенье 21 марта, Пасха отмечается через 7 дней, а если полнолуние приходится на субботу 21 марта, Пасха отмечается 22 марта.
Вторая часть — нахождение e , дополнительных дней смещения, которые необходимо добавить к смещению даты d , чтобы оно пришло в воскресенье. Поскольку в неделе 7 дней, смещение должно быть в диапазоне от 0 до 6 и определяться арифметикой по модулю 7. e определяется путем вычисления 2 b + 4 c + 6 d + N mod 7. Эти константы могут показаться странными на первый взгляд, но их довольно легко объяснить, если вспомнить, что мы работаем в арифметике по модулю 7. Для начала, 2 b + 4 c гарантирует, что мы учтем тот факт, что дни недели сдвигаются для каждого года.
Обычный год состоит из 365 дней, но 52 × 7 = 364 , поэтому 52 полных недели составляют один день, которого не хватает. Таким образом, каждый последующий год, день недели «сдвигается на один день вперед», то есть, если 6 мая было средой в одном году, то в следующем году это будет четверг (без учета високосных лет). И b, и c увеличиваются на единицу для продвижения на один год (без учета модульных эффектов). Выражение 2 b + 4 c , таким образом, увеличивается на 6 — но помните, что это то же самое, что вычитание 1 mod 7.
Вычитание на 1 — это именно то, что требуется для обычного года — поскольку будний день сдвигается на один день вперед, мы должны компенсировать на один день меньше, чтобы получить правильный будний день (т. е. воскресенье). Для високосного года b становится 0, а 2 b, таким образом, равно 0 вместо 8 — что по модулю 7 является еще одним вычитанием на 1 — т. е. полным вычитанием на 2, поскольку будние дни после високосного дня в этом году сдвигаются вперед на два дня.
Выражение 6 d работает таким же образом. Увеличение d на некоторое число y указывает, что полнолуние произойдет на y дней позже в этом году, и, следовательно, мы должны компенсировать на y дней меньше. Добавление 6 d по модулю 7 то же самое, что и вычитание d , что и является желаемой операцией. Таким образом, мы снова выполняем вычитание, добавляя по модулю арифметики. В общей сложности переменная e содержит шаг от дня после дня полнолуния до ближайшего следующего воскресенья, между 0 и 6 днями вперед. Константа N обеспечивает отправную точку для вычислений для каждого столетия и зависит от того, где неявно располагалось 1 января года 1 при построении григорианского календаря.
Выражение d + e может давать смещения в диапазоне от 0 до 35, указывающие на возможные пасхальные воскресенья с 22 марта по 26 апреля. По причинам исторической совместимости все смещения 35 и некоторые из 34 вычитаются на 7, переходя на одно воскресенье назад к дню полнолуния (фактически используя отрицательное e, равное −1). Это означает, что 26 апреля никогда не является пасхальным воскресеньем, а 19 апреля представлено сверх меры. Эти последние исправления сделаны только по историческим причинам и не имеют ничего общего с математическим алгоритмом. Смещение 34 корректируется, если (и только если) d = 28 и d = 29 в другом месте 19-летнего цикла.
Использование алгоритма Пасхи Гаусса для лет до 1583 года исторически бессмысленно, поскольку григорианский календарь не использовался для определения Пасхи до этого года. Использование алгоритма в далеком будущем сомнительно, поскольку мы ничего не знаем о том, как разные церкви будут определять Пасху в далеком будущем. Расчеты Пасхи основаны на соглашениях и конвенциях, а не на реальных небесных движениях или неоспоримых фактах истории.
«Нью-йоркский корреспондент» представил этот алгоритм определения григорианской Пасхи в журнал Nature в 1876 году. [74] [75] Он был переиздан много раз, например, в 1877 году Сэмюэлем Бутчером в The Ecclesiastical Calendar , [76] в 1916 году Артуром Даунингом в The Observatory , [77] в 1922 году Х. Спенсером Джонсом в General Astronomy , [78] в 1977 году Journal of the British Astronomical Association , [79] в 1977 году The Old Farmer's Almanac , в 1988 году Питером Даффетом-Смитом в Practical Astronomy with your Calculator и в 1991 году Джином Миусом в Astronomical Algorithms . [80] Из-за цитирования книги Миуса этот алгоритм также называют «алгоритм Миуса/Джонса/Батчера»:
В этом алгоритме переменная n указывает месяц года (март для n = 3 или апрель для n = 4), а день месяца получается как ( o + 1). В 1961 году New Scientist опубликовал версию алгоритма Nature , включающую несколько изменений. [81] Переменная g была рассчитана с использованием поправки Гаусса 1816 года, что привело к исключению переменной f . Некоторая очистка приводит к замене переменной o (к которой нужно прибавить единицу, чтобы получить дату Пасхи) на переменную p , которая дает дату напрямую.
Жан Меус в своей книге «Астрономические алгоритмы» (1991, стр. 69) представляет следующий алгоритм для расчета юлианской Пасхи по юлианскому календарю, который не является григорианским календарем, используемым в качестве гражданского календаря в большинстве стран современного мира. Чтобы получить дату Восточной православной Пасхи по последнему календарю, к юлианским датам необходимо добавить 13 дней (с 1900 по 2099 год), получив в результате даты, указанные ниже, в последней строке. (До 2099 года нашей эры 21 марта по юлианскому календарю соответствует 3 апреля по григорианскому календарю.)
{{cite book}}: CS1 maint: location missing publisher (link){{cite journal}}: |author=имеет общее название ( помощь )