Прогиб (инженерный)

Degree to which part of a structural element is displaced under a given load

Прогиб (f) в машиностроении

В строительной инженерии прогиб — это степень, в которой часть длинного структурного элемента (например, балки ) деформируется в поперечном направлении (в направлении, поперечном его продольной оси) под нагрузкой . Он может быть количественно определен в терминах угла ( угловое смещение ) или расстояния (линейное смещение ). Продольная деформация (в направлении оси) называется удлинением .

Расстояние прогиба элемента под нагрузкой можно рассчитать путем интегрирования функции, которая математически описывает наклон прогибаемой формы элемента под этой нагрузкой. Существуют стандартные формулы для прогиба обычных конфигураций балок и случаев нагрузки в дискретных местах. В противном случае используются такие методы, как виртуальная работа , прямое интегрирование , метод Кастильяно , метод Маколея или метод прямой жесткости . Прогиб элементов балки обычно рассчитывается на основе уравнения балки Эйлера-Бернулли, тогда как прогиб элемента пластины или оболочки рассчитывается с использованием теории пластины или оболочки .

Примером использования прогиба в этом контексте является строительство зданий. Архитекторы и инженеры выбирают материалы для различных применений.

Прогиб балки при различных нагрузках и опорах

Балки могут сильно различаться по своей геометрии и составу. Например, балка может быть прямой или изогнутой. Она может иметь постоянное поперечное сечение или может сужаться. Она может быть сделана полностью из одного и того же материала (однородная) или может состоять из разных материалов (композитная). Некоторые из этих вещей затрудняют анализ, но многие инженерные приложения включают случаи, которые не столь сложны. Анализ упрощается, если:

• Изначально балка прямая, и любое сужение незначительное.
• Балка испытывает только линейную упругую деформацию
• Балка тонкая (отношение ее длины к высоте больше 10)
• Рассматриваются только небольшие прогибы (максимальный прогиб менее 1/10 пролета ) .

В этом случае уравнение, определяющее прогиб балки ( ), можно аппроксимировать следующим образом: где вторая производная ее прогнутой формы относительно ( горизонтального положения по длине балки) интерпретируется как ее кривизна, — модуль Юнга , — момент инерции площади поперечного сечения, — внутренний изгибающий момент в балке. ${\displaystyle w}$ $${\displaystyle {\frac {\mathrm {d} ^{2}w(x)}{\mathrm {d} x^{2}}}={\frac {M(x)}{E(x)I(x)}}}$$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle E}$ ${\displaystyle I}$ ${\displaystyle M}$

Если, кроме того, балка не имеет конической формы, однородна и на нее действует распределенная нагрузка , то приведенное выше выражение можно записать в виде : ${\displaystyle q}$ ${\displaystyle EI~{\frac {\mathrm {d} ^{4}w(x)}{\mathrm {d} x^{4}}}=q(x)}$

Это уравнение можно решить для различных условий нагрузки и граничных условий. Ниже приведен ряд простых примеров. Выраженные формулы являются приближениями, разработанными для длинных, тонких, однородных, призматических балок с малыми прогибами и линейными упругими свойствами. При этих ограничениях приближения должны давать результаты в пределах 5% от фактического прогиба.

Консольные балки

Консольные балки имеют один закрепленный конец, поэтому наклон и прогиб на этом конце должны быть равны нулю.

Схема прогиба консольной балки.

Консольные балки с торцевой нагрузкой

Консольная балка с усилием на свободном конце

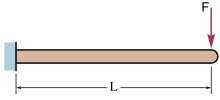
Упругий прогиб и угол прогиба (в радианах ) на свободном конце в примере изображения: (Невесомая) консольная балка с конечной нагрузкой может быть рассчитана (на свободном конце B) с помощью: ^[1 ] где ${\displaystyle \delta }$ ${\displaystyle \phi }$ $${\displaystyle {\begin{aligned}\delta _{B}&={\frac {FL^{3}}{3EI}}\\[1ex]\phi _{B}&={\frac {FL^{2}}{2EI}}\end{aligned}}}$$

• ${\displaystyle F}$= сила, действующая на кончик балки
• ${\displaystyle L}$= длина балки (пролет)
• ${\displaystyle E}$= модуль упругости
• ${\displaystyle I}$= момент инерции площади поперечного сечения балки

Обратите внимание, что если пролет удваивается, прогиб увеличивается в восемь раз. Прогиб в любой точке, , вдоль пролета консольной балки с торцевой нагрузкой можно рассчитать с помощью: ^[1] ${\displaystyle x}$ $${\displaystyle {\begin{aligned}\delta _{x}&={\frac {Fx^{2}}{6EI}}(3L-x)\\[1ex]\phi _{x}&={\frac {Fx}{2EI}}(2L-x)\end{aligned}}}$$

Примечание: На (конце балки) уравнения и идентичны уравнениям и выше. ${\displaystyle x=L}$ ${\displaystyle \delta _{x}}$ ${\displaystyle \phi _{x}}$ ${\displaystyle \delta _{B}}$ ${\displaystyle \phi _{B}}$

Равномерно нагруженные консольные балки

Консольная балка с равномерно распределенной нагрузкой

Прогиб на свободном конце B консольной балки под равномерной нагрузкой определяется по формуле: ^[1] где $${\displaystyle {\begin{aligned}\delta _{B}&={\frac {qL^{4}}{8EI}}\\[1ex]\phi _{B}&={\frac {qL^{3}}{6EI}}\end{aligned}}}$$

• ${\displaystyle q}$= равномерная нагрузка на балку (сила на единицу длины)
• ${\displaystyle L}$= длина балки
• ${\displaystyle E}$= модуль упругости
• ${\displaystyle I}$= момент инерции площади поперечного сечения

Прогиб в любой точке вдоль пролета равномерно нагруженной консольной балки можно рассчитать с помощью: ^[1] ${\displaystyle x}$ $${\displaystyle {\begin{aligned}\delta _{x}&={\frac {qx^{2}}{24EI}}\left(6L^{2}-4Lx+x^{2}\right)\\[1ex]\phi _{x}&={\frac {qx}{6EI}}\left(3L^{2}-3Lx+x^{2}\right)\end{aligned}}}$$

Просто опертые балки

Простые балки имеют опоры под концами, которые допускают вращение, но не прогиб.

Схема прогиба просто опертой балки.

Простые балки с центральной нагрузкой

Просто опертая балка с силой в центре

Прогиб в любой точке вдоль пролета центральной нагруженной просто опертой балки можно рассчитать с помощью: ^[1] для ${\displaystyle x}$ $${\displaystyle \delta _{x}={\frac {Fx}{48EI}}\left(3L^{2}-4x^{2}\right)}$$ $${\displaystyle 0\leq x\leq {\frac {L}{2}}}$$

Частный случай упругого прогиба в средней точке C балки, нагруженной в ее центре и поддерживаемой двумя простыми опорами, тогда задается выражением: ^[1] где $${\displaystyle \delta _{C}={\frac {FL^{3}}{48EI}}}$$

• ${\displaystyle F}$= сила, действующая на центр балки
• ${\displaystyle L}$= длина балки между опорами
• ${\displaystyle E}$= модуль упругости
• ${\displaystyle I}$= момент инерции площади поперечного сечения

Простые балки с нецентральной нагрузкой

Просто опертая балка с силой, действующей вне центра

Максимальный упругий прогиб балки, опирающейся на две простые опоры, нагруженной на расстоянии от ближайшей опоры, определяется по формуле: ^[1] где ${\displaystyle a}$ $${\displaystyle \delta _{\text{max}}={\frac {Fa\left(L^{2}-a^{2}\right)^{3/2}}{9{\sqrt {3}}LEI}}}$$

• ${\displaystyle F}$= сила, действующая на балку
• ${\displaystyle L}$= длина балки между опорами
• ${\displaystyle E}$= модуль упругости
• ${\displaystyle I}$= момент инерции площади поперечного сечения
• ${\displaystyle a}$= расстояние от груза до ближайшей опоры

Этот максимальный прогиб происходит на расстоянии от ближайшей опоры и определяется по формуле: ^[1] ${\displaystyle x_{1}}$ $${\displaystyle x_{1}={\sqrt {\frac {L^{2}-a^{2}}{3}}}}$$

Равномерно нагруженные простые балки

Простая опорная балка с равномерно распределенной нагрузкой

Упругий прогиб (в средней точке C) балки, поддерживаемой двумя простыми опорами, под равномерной нагрузкой (как показано на рисунке), определяется по формуле: ^[1] где $${\displaystyle \delta _{C}={\frac {5qL^{4}}{384EI}}}$$

• ${\displaystyle q}$= равномерная нагрузка на балку (сила на единицу длины)
• ${\displaystyle L}$= длина балки
• ${\displaystyle E}$= модуль упругости
• ${\displaystyle I}$= момент инерции площади поперечного сечения

Прогиб в любой точке вдоль пролета равномерно нагруженной просто опертой балки можно рассчитать с помощью формулы: ^[1] ${\displaystyle x}$ $${\displaystyle \delta _{x}={\frac {qx}{24EI}}\left(L^{3}-2Lx^{2}+x^{3}\right)}$$

Комбинированные нагрузки

Прогиб балок при комбинированном действии простых нагрузок можно рассчитать с помощью принципа суперпозиции .

Изменение длины

Изменение длины балки, спроецированное вдоль линии ненагруженной балки, можно рассчитать путем интегрирования функции наклона , если известна функция прогиба для всех . ${\displaystyle \Delta L}$ ${\displaystyle \theta _{x}}$ ${\displaystyle \delta _{x}}$ ${\displaystyle x}$

Где:

• ${\displaystyle \Delta L}$= изменение длины (всегда отрицательное)
• ${\displaystyle \theta _{x}}$= функция наклона (первая производная ) ${\displaystyle \delta _{x}}$
• ${\displaystyle \Delta L=-{\frac {1}{2}}\int _{0}^{L}(\theta (x))^{2}dx}$^[2]

Если балка однородна и прогиб в любой точке известен, то его можно рассчитать, не зная других свойств балки.

Единицы

Формулы, приведенные выше, требуют использования согласованного набора единиц. Большинство расчетов будут выполнены в Международной системе единиц (СИ) или в традиционных единицах США, хотя существует много других систем единиц.

Международная система (СИ)

• Сила: ньютоны ( ) ${\displaystyle \mathrm {N} }$
• Длина: метров ( ) ${\displaystyle \mathrm {m} }$
• Модуль упругости: ${\displaystyle \mathrm {\frac {N}{m^{2}}} =\mathrm {Pa} }$
• Момент инерции: ${\displaystyle \mathrm {m^{4}} }$

Единицы измерения США (США)

• Сила: фунты силы ( ) ${\displaystyle \mathrm {lbf} }$
• Длина: дюймы ( ) ${\displaystyle \mathrm {in} }$
• Модуль упругости: ${\displaystyle \mathrm {\frac {lbf}{in^{2}}} }$
• Момент инерции: ${\displaystyle \mathrm {in^{4}} }$

Другие

Другие единицы измерения также могут использоваться, если они являются самосогласованными. Например, иногда для измерения нагрузок используется единица килограмм-сила ( ). В таком случае модуль упругости должен быть преобразован в . ${\displaystyle \mathrm {kgf} }$ ${\displaystyle \mathrm {\frac {kgf}{m^{2}}} }$

Прогиб конструкции

Строительные нормы определяют максимальный прогиб, обычно как часть пролета, например, 1/400 или 1/600. Минимальные размеры требуемого элемента могут определяться либо предельным состоянием прочности (допустимое напряжение), либо предельным состоянием эксплуатационной пригодности (соображения прогиба среди прочего).

Прогиб должен учитываться для целей конструкции. При проектировании стальной рамы для удержания стеклянной панели допускается лишь минимальный прогиб, чтобы предотвратить разрушение стекла.

Изогнутую форму балки можно представить с помощью диаграммы моментов , проинтегрированной (дважды, повернутой и смещенной для обеспечения условий опоры).

Смотрите также

• Метод отклонения склона

Ссылки

1. Gere, James M.; Goodno, Barry J. (январь 2012 г.). Механика материалов (восьмое изд.). стр. 1083–1087. ISBN 978-1-111-57773-5.
2. Формулы Рорка для напряжения и деформации, 8-е издание, уравнение 8.1-14

Внешние ссылки

• Прогиб балок
• Отклонения балки
• Инструменты расчета прогиба и наклона балок