stringtranslate.com

Прототайл

Эта форма апериодической мозаики Пенроуза имеет две протоплитки: толстый ромб (показан на рисунке синим цветом) и тонкий ромб (зеленым цветом).

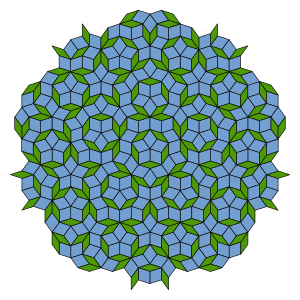
В математике протоплитка — это одна из форм плитки в мозаике . [1]

Определение

Тесселяция плоскости или любого другого пространства — это покрытие пространства замкнутыми фигурами, называемыми плитками, которые имеют непересекающиеся внутренние части . Некоторые плитки могут быть конгруэнтны одной или нескольким другим. Если S — набор плиток в тесселяции, набор R фигур называется набором протоплиток, если никакие две фигуры в R не конгруэнтны друг другу, и каждая плитка в S конгруэнтна одной из фигур в R. [2]

Можно выбрать много различных наборов протоплиток для мозаики: перемещение или поворот любого из протоплиток создает другой допустимый набор протоплиток. Однако каждый набор протоплиток имеет одинаковую мощность , поэтому количество протоплиток хорошо определено. Тесселяция называется моноэдральной , если она имеет ровно одну протоплитку.

Апериодичность

Плитка, которая не повторяется и использует только одну форму, открытая Дэвидом Смитом.

Набор протоплиток называется апериодическим, если каждая мозаика с этими протоплитками является апериодической мозаикой . В марте 2023 года четыре исследователя, Хаим Гудман-Штраус , Дэвид Смит , Джозеф Сэмюэл Майерс и Крейг С. Каплан, объявили об открытии апериодической моноэдральной протоплитки (монотили) и доказательстве того, что плитка, открытая Дэвидом Смитом, является апериодической монотили, то есть решением давней открытой проблемы Эйнштейна . [3] [4]

В более высоких размерностях проблема была решена ранее: плитка Шмитта-Конвея-Данцера является протоплиткой моноэдральной апериодической мозаики трехмерного евклидова пространства и не может замостить пространство периодически.

Ссылки

  1. ^ Седерберг, Джудит Н. (2001), Курс современной геометрии, Бакалаврские тексты по математике (2-е изд.), Springer-Verlag, стр. 174, ISBN 978-0-387-98972-3.
  2. ^ Каплан, Крейг С. (2009), Вводная теория мозаики для компьютерной графики, Лекции по синтезу компьютерной графики и анимации, Morgan & Claypool Publishers, стр. 7, ISBN 978-1-60845-017-6.
  3. ^ Робертс, Сиобхан (28.03.2023). «Неуловимый «Эйнштейн» решает давнюю математическую задачу». The New York Times . ISSN  0362-4331 . Получено 02.06.2023 .
  4. ^ Смит, Дэвид; Джозеф Сэмюэл Майерс ; Каплан, Крейг С.; Гудман-Штраус, Хаим (2024). «Апериодическая моноплитка». Комбинаторная теория . 4. arXiv : 2303.10798 . doi : 10.5070/C64163843.