Процентиль

Статистика, которая делит набор данных на 100 частей и анализирует их в процентах.

В статистике k -й процентиль , также известный как процентильный балл или центиль , — это балл , ниже которого падает заданный процент k баллов в его частотном распределении (« исключительное » определение), или балл, на который или ниже которого падает заданный процент (« включительное » определение). Процентили выражаются в той же единице измерения , что и входные баллы, а не в процентах ; например, если баллы относятся к весу человека , соответствующие процентили будут выражены в килограммах или фунтах. В пределе бесконечного размера выборки процентиль аппроксимирует процентильную функцию , обратную кумулятивной функции распределения .

Процентили — это тип квантилей , получаемых путем деления на 100 групп. 25-й процентиль также известен как первый квартиль ( Q ₁ ), 50-й процентиль — как медиана или второй квартиль ( Q ₂ ), а 75-й процентиль — как третий квартиль ( Q ₃ ). Например, 50-й процентиль (медиана) — это оценка ниже (или на уровне или ниже , в зависимости от определения), которой соответствуют 50% оценок в распределении.

Связанная величина — это процентильный ранг оценки, выраженный в процентах , который представляет собой долю оценок в его распределении, которые меньше его, исключительное определение. Процентильные баллы и процентильные ранги часто используются при сообщении результатов тестов , относящихся к норме , но, как только что было отмечено, они не одно и то же. Для процентильных рангов дается балл и вычисляется процент. Процентильные ранги являются исключительными: если процентильный ранг для указанной оценки составляет 90%, то 90% оценок были ниже. Напротив, для процентилей дается процент и определяется соответствующая оценка, которая может быть как исключающей, так и инклюзивной. Оценка для указанного процента (например, 90-й) указывает оценку, ниже которой (исключающее определение) или на уровне или ниже которой (включающее определение) находятся другие оценки в распределении.

Определения

Стандартного определения процентиля не существует; ^{[1] [2] [3]} однако все определения дают схожие результаты, когда число наблюдений очень велико, а распределение вероятностей непрерывно. ^[4] В пределе, когда размер выборки стремится к бесконечности, 100 ^{-й процентиль} p (0< p <1) приближается к обратной величине кумулятивной функции распределения (CDF), сформированной таким образом, оцененной при p , поскольку p приближается к CDF. Это можно рассматривать как следствие теоремы Гливенко–Кантелли . Некоторые методы расчета процентилей приведены ниже.

Нормальное распределение и процентили

Представление правила трех сигм . Темно-синяя зона представляет наблюдения в пределах одного стандартного отклонения (σ) по обе стороны от среднего значения (μ), что составляет около 68,3% популяции. Два стандартных отклонения от среднего значения (темно- и средне-синие) составляют около 95,4%, а три стандартных отклонения (темно-, средне- и светло-синие) — около 99,7%.

Методы, приведенные в разделе методов расчета (ниже), являются приближениями для использования в статистике малых выборок. В общих чертах, для очень больших популяций, следующих нормальному распределению , процентили часто могут быть представлены ссылкой на график нормальной кривой. Нормальное распределение строится вдоль оси, масштабированной до стандартных отклонений , или единиц сигма ( ). Математически нормальное распределение простирается до отрицательной бесконечности слева и положительной бесконечности справа. Обратите внимание, однако, что только очень небольшая доля людей в популяции будет выходить за пределы диапазона от −3 σ до +3 σ . Например, при росте человека очень немногие люди выше уровня роста +3 σ . ${\displaystyle \sigma }$

Процентили представляют собой площадь под нормальной кривой, увеличиваясь слева направо. Каждое стандартное отклонение представляет собой фиксированный процентиль. Таким образом, округляя до двух знаков после запятой, −3 σ — это 0,13-й процентиль, −2 σ — 2,28-й процентиль, −1 σ — 15,87-й процентиль, 0 σ — 50-й процентиль (как среднее, так и медиана распределения), +1 σ — 84,13-й процентиль, +2 σ — 97,72-й процентиль и +3 σ — 99,87-й процентиль. Это связано с правилом 68–95–99,7 или правилом трех сигм. Обратите внимание, что теоретически 0-й процентиль приходится на отрицательную бесконечность, а 100-й процентиль — на положительную бесконечность, хотя во многих практических приложениях, таких как результаты испытаний, применяются естественные нижние и/или верхние пределы.

Приложения

Когда интернет-провайдеры выставляют счет за «взрывную» пропускную способность интернета , 95-й или 98-й процентиль обычно отсекает верхние 5% или 2% пиков пропускной способности в каждом месяце, а затем выставляет счет по ближайшему тарифу. Таким образом, нечастые пики игнорируются, и клиент платит более справедливо. Причина, по которой эта статистика так полезна для измерения пропускной способности данных, заключается в том, что она дает очень точную картину стоимости пропускной способности. 95-й процентиль говорит, что 95% времени использование ниже этой суммы: поэтому оставшиеся 5% времени использование выше этой суммы.

Врачи часто используют вес и рост младенцев и детей для оценки их развития в сравнении со средними показателями по стране и процентилями, указанными в диаграммах роста .

85-й процентиль скорости движения на дороге часто используется в качестве ориентира при установлении ограничений скорости и оценке того, является ли такое ограничение слишком высоким или низким. ^{[5] [6]}

В финансах стоимость под риском — это стандартная мера оценки (в зависимости от модели) величины, ниже которой стоимость портфеля, как ожидается, не упадет в течение определенного периода времени и с учетом доверительного значения.

Методы расчета

Интерполированные и ближайшие по рангу, исключительные и инклюзивные, процентили для 10-балльного распределения

Интерполированные и ближайшие по рангу, исключительные и инклюзивные, процентили для 10-балльного распределения

Существует множество формул или алгоритмов ^[7] для процентильного балла. Хайндман и Фэн ^[1] выделили девять, и большинство статистических и табличных программ используют один из описанных ими методов. ^[8] Алгоритмы либо возвращают значение балла, существующего в наборе баллов (методы ближайшего ранга), либо интерполируют между существующими баллами и являются либо исключающими, либо инклюзивными.

Рисунок показывает распределение с 10 баллами, иллюстрирует процентильные баллы, которые получаются из этих различных алгоритмов, и служит введением к примерам, приведенным далее. Простейшими являются методы ближайшего ранга, которые возвращают балл из распределения, хотя по сравнению с методами интерполяции результаты могут быть немного грубыми. Таблица методов ближайшего ранга показывает вычислительные шаги для исключающих и инклюзивных методов.

Методы интерполяции, как следует из названия, могут возвращать оценку, которая находится между оценками в распределении. Алгоритмы, используемые статистическими программами, обычно используют методы интерполяции, например, функции percentile.exc и percentile.inc в Microsoft Excel. Таблица Interpolated Methods показывает вычислительные шаги.

Метод ближайшего ранга

Значения процентиля для упорядоченного списка {15, 20, 35, 40, 50}

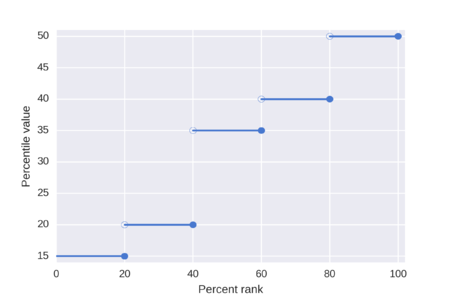
Одно из определений процентиля, часто приводимое в текстах, заключается в том, что P -й процентиль списка из N упорядоченных значений (отсортированных от наименьшего к наибольшему) является наименьшим значением в списке, таким, что не более P процентов данных строго меньше значения и по крайней мере P процентов данных меньше или равны этому значению. Это получается путем первого вычисления порядкового ранга, а затем взятия значения из упорядоченного списка, соответствующего этому рангу. Порядковый ранг n вычисляется с использованием этой формулы ${\displaystyle (0<P\leq 100)}$

${\displaystyle n=\left\lceil {\frac {P}{100}}\times N\right\rceil .}$

• Использование метода ближайшего ранга в списках, содержащих менее 100 различных значений, может привести к тому, что одно и то же значение будет использоваться для более чем одного процентиля.
• Процентиль, рассчитанный с использованием метода ближайшего ранга, всегда будет членом исходного упорядоченного списка.
• 100-й процентиль определяется как наибольшее значение в упорядоченном списке.

Метод линейной интерполяции между ближайшими рангами

Альтернативой округлению, используемому во многих приложениях, является использование линейной интерполяции между соседними рангами.

Все следующие варианты имеют следующее общее. Учитывая статистику заказов

${\displaystyle \{v_{i},i=1,2,\ldots ,N:v_{i+1}\geq v_{i},\forall i=1,2,\ldots ,N-1\},}$

мы ищем линейную интерполяционную функцию, проходящую через точки . Это просто достигается путем ${\displaystyle (v_{i},i)}$

${\displaystyle v(x)=v_{\lfloor x\rfloor }+(x{\bmod {1}})(v_{\lfloor x\rfloor +1}-v_{\lfloor x\rfloor }),\forall x\in [1,N]:v(i)=v_{i}{\text{, for }}i=1,2,\ldots ,N,}$

где использует функцию floor для представления целой части положительного x , тогда как использует функцию mod для представления его дробной части (остаток после деления на 1). (Обратите внимание, что, хотя в конечной точке , не определено, это не обязательно так, поскольку оно умножается на .) Как мы видим, x является непрерывной версией индекса i , линейно интерполирующей v между соседними узлами. ${\displaystyle \lfloor x\rfloor }$ ${\displaystyle x{\bmod {1}}}$ ${\displaystyle x=N}$ ${\displaystyle v_{\lfloor x\rfloor +1}}$ ${\displaystyle x{\bmod {1}}=0}$

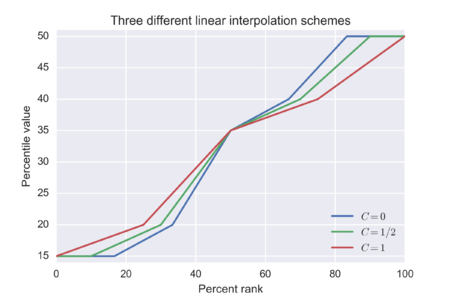
Есть два способа, которыми различаются варианты подходов. Первый заключается в линейной зависимости между рангом x , процентным рангом и константой, которая является функцией размера выборки N : ${\displaystyle P=100p}$

${\displaystyle x=f(p,N)=(N+c_{1})p+c_{2}.}$

Существует дополнительное требование, чтобы средняя точка диапазона , соответствующая медиане , находилась в : ${\displaystyle (1,N)}$ ${\displaystyle p=0.5}$

${\displaystyle {\begin{aligned}f(0.5,N)&={\frac {N+c_{1}}{2}}+c_{2}={\frac {N+1}{2}}\\\therefore 2c_{2}+c_{1}&=1\end{aligned}},}$

и наша пересмотренная функция теперь имеет только одну степень свободы и выглядит следующим образом:

${\displaystyle x=f(p,N)=(N+1-2C)p+C.}$

Второй способ, которым варианты различаются, заключается в определении функции вблизи границ диапазона p : должна производить или быть вынуждена производить результат в диапазоне , что может означать отсутствие однозначного соответствия в более широкой области. Один автор предложил выбор , где ξ — форма обобщенного распределения экстремальных значений , которое является пределом экстремальных значений выборочного распределения. ${\displaystyle [0,1]}$ ${\displaystyle f(p,N)}$ ${\displaystyle [1,N]}$ ${\displaystyle C={\tfrac {1}{2}}(1+\xi )}$

Первый вариант,С= 1/2

Результат использования каждого из трех вариантов в упорядоченном списке {15, 20, 35, 40, 50}

(Источники: функция Matlab "prctile", ^{[9] [10]} )

${\displaystyle x=f(p)={\begin{cases}Np+{\frac {1}{2}},\forall p\in \left[p_{1},p_{N}\right],\\1,\forall p\in \left[0,p_{1}\right],\\N,\forall p\in \left[p_{N},1\right].\end{cases}}}$

где

${\displaystyle p_{i}={\frac {1}{N}}\left(i-{\frac {1}{2}}\right),i\in [1,N]\cap \mathbb {N} }$

${\displaystyle \therefore p_{1}={\frac {1}{2N}},p_{N}={\frac {2N-1}{2N}}.}$

Кроме того, пусть

${\displaystyle P_{i}=100p_{i}.}$

Обратная зависимость ограничена более узкой областью:

${\displaystyle p={\frac {1}{N}}\left(x-{\frac {1}{2}}\right),x\in (1,N)\cap \mathbb {R} .}$

Второй вариант,С= 1

[Источник: Некоторые программные пакеты, включая NumPy ^[11] и Microsoft Excel ^[3] (до версии 2013 включительно с помощью функции PERCENTILE.INC). Отмечено как альтернатива NIST . ^[8] ]

${\displaystyle x=f(p,N)=p(N-1)+1{\text{, }}p\in [0,1]}$

${\displaystyle \therefore p={\frac {x-1}{N-1}}{\text{, }}x\in [1,N].}$

Обратите внимание, что связь является один-к-одному для , единственного из трех вариантов с этим свойством; отсюда суффикс «INC» ( включительно ) в функции Excel. ${\displaystyle x\leftrightarrow p}$ ${\displaystyle p\in [0,1]}$

Третий вариант,С= 0

(Основной вариант, рекомендованный NIST . ^[8] Принят в Microsoft Excel с 2010 года посредством функции PERCENTIL.EXC. Однако, как указывает суффикс «EXC», версия Excel исключает обе конечные точки диапазона p , т. е. , тогда как версия «INC», второй вариант, этого не делает; фактически, любое число, меньшее , также исключается и приведет к ошибке.) ${\displaystyle p\in (0,1)}$ ${\displaystyle {\frac {1}{N+1}}}$

${\displaystyle x=f(p,N)={\begin{cases}1{\text{, }}p\in \left[0,{\frac {1}{N+1}}\right]\\p(N+1){\text{, }}p\in \left({\frac {1}{N+1}},{\frac {N}{N+1}}\right)\\N{\text{, }}p\in \left[{\frac {N}{N+1}},1\right]\end{cases}}.}$

Обратное уравнение ограничено более узкой областью:

${\displaystyle p={\frac {x}{N+1}}{\text{, }}x\in (0,N).}$

Метод взвешенного процентиля

В дополнение к функции процентиля, есть также взвешенный процентиль , где вместо общего числа подсчитывается процент в общем весе. Стандартной функции для взвешенного процентиля не существует. Один метод естественным образом расширяет вышеуказанный подход.

Предположим, что у нас есть положительные веса , связанные, соответственно, с нашими N отсортированными выборочными значениями. Пусть ${\displaystyle w_{1},w_{2},w_{3},\dots ,w_{N}}$

${\displaystyle S_{N}=\sum _{k=1}^{N}w_{k},}$

сумма весов. Затем формулы выше обобщаются, принимая

${\displaystyle p_{n}={\frac {1}{S_{N}}}\left(S_{n}-{\frac {w_{n}}{2}}\right)}$когда , ${\displaystyle C=1/2}$

или

${\displaystyle p_{n}={\frac {S_{n}-Cw_{n}}{S_{N}+(1-2C)w_{n}}}}$для общего , ${\displaystyle C}$

и

${\displaystyle v=v_{k}+{\frac {P-p_{k}}{p_{k+1}-p_{k}}}(v_{k+1}-v_{k}).}$

50%-ный взвешенный процентиль известен как взвешенная медиана .

Смотрите также

• Математический портал

• Дециль
• Процентильный ранг
• Квантиль
• Сводная статистика

Ссылки

1. Hyndman, Rob J. ; Fan, Yanan (ноябрь 1996 г.). «Выборочные квантили в статистических пакетах». American Statistician . 50 (4). Американская статистическая ассоциация: 361–365. doi :10.2307/2684934. JSTOR  2684934.
2. Лейн, Дэвид. "Процентили" . Получено 15 сентября 2007 г.
3. Pottel, Hans. "Статистические недостатки Excel" (PDF) . Архивировано из оригинала (PDF) 2013-06-04 . Получено 2013-03-25 .
4. Schoonjans F, De Bacquer D, Schmid P (2011). «Оценка процентилей населения». Эпидемиология . 22 (5): 750–751. doi : 10.1097/EDE.0b013e318225c1de. PMC 3171208. PMID  21811118. 
5. Джонсон, Роберт; Куби, Патрисия (2007), «Прикладной пример 2.15, 85-й процентиль ограничения скорости: движение с 85% потока», Elementary Statistics (10-е изд.), Cengage Learning, стр. 102, ISBN 9781111802493.
6. "Рациональные ограничения скорости и 85-й процентиль скорости" (PDF) . lsp.org . Полиция штата Луизиана. Архивировано из оригинала (PDF) 23 сентября 2018 г. . Получено 28 октября 2018 г. .
7. Wessa, P (2021). «Процентили в бесплатном статистическом программном обеспечении». Office for Research Development and Education . Получено 13 ноября 2021 г.
8. "Справочник по инженерной статистике: Процентиль". NIST . Получено 18.02.2009 .
9. "Matlab Statistics Toolbox – Percentiles" . Получено 2006-09-15 ., Это эквивалентно методу 5, обсуждаемому здесь
10. Лэнгфорд, Э. (2006). «Квартили в элементарной статистике». Журнал статистического образования . 14 (3). doi : 10.1080/10691898.2006.11910589 .
11. "Документация NumPy 1.12". SciPy . Получено 2017-03-19 .