Круговое движение

Движение объекта по круговой траектории

В физике круговое движение — это движение объекта по окружности или вращение по дуге окружности . Оно может быть равномерным, с постоянной скоростью вращения и постоянной тангенциальной скоростью , или неравномерным с изменяющейся скоростью вращения. Вращение вокруг неподвижной оси трехмерного тела предполагает круговое движение его частей. Уравнения движения описывают движение центра масс тела, который остается на постоянном расстоянии от оси вращения . При круговом движении расстояние между телом и неподвижной точкой на его поверхности остается прежним, т. е. тело предполагается жестким .

Примерами кругового движения являются: специальные спутниковые орбиты вокруг Земли ( круговые орбиты ), лопасти потолочного вентилятора, вращающиеся вокруг ступицы, камень, привязанный к веревке и раскачиваемый по кругу, автомобиль, поворачивающий по кривой на гоночной трассе , электрон, движущийся перпендикулярно однородному магнитному полю , и шестерня, вращающаяся внутри механизма.

Поскольку вектор скорости объекта постоянно меняет направление, движущийся объект испытывает ускорение под действием центростремительной силы в направлении центра вращения. Без этого ускорения объект двигался бы по прямой линии, согласно законам движения Ньютона .

Равномерное круговое движение

Рисунок 1: Скорость v и ускорение a при равномерном круговом движении с угловой скоростью ω ; скорость постоянна, но скорость всегда направлена ​​по касательной к орбите; ускорение имеет постоянную величину, но всегда направлено к центру вращения.

Рисунок 2: Векторы скорости в моменты времени t и t + dt перемещаются с орбиты слева в новые положения, где их хвосты совпадают, справа. Поскольку скорость фиксирована по величине при v = r ω , векторы скорости также описывают круговую траекторию с угловой скоростью ω . При dt → 0 вектор ускорения a становится перпендикулярным v , что означает, что он указывает на центр орбиты в круге слева. Угол ω dt является очень малым углом между двумя скоростями и стремится к нулю при dt → 0 .

Рисунок 3: (Слева) Мяч совершает круговое движение — веревка создает центростремительную силу, удерживающую мяч в круге. (Справа) Веревка перерезана, а мяч продолжает движение по прямой со скоростью в момент перерезания веревки в соответствии с законом инерции Ньютона, поскольку центростремительной силы больше нет.

В физике равномерное круговое движение описывает движение тела, движущегося по круговой траектории с постоянной скоростью . Поскольку тело совершает круговое движение, его расстояние от оси вращения остается постоянным во все времена. Хотя скорость тела постоянна, его скорость не постоянна: скорость, векторная величина, зависит как от скорости тела, так и от направления его движения. Эта изменяющаяся скорость указывает на наличие ускорения; это центростремительное ускорение имеет постоянную величину и направлено во все времена к оси вращения. Это ускорение, в свою очередь, создается центростремительной силой , которая также постоянна по величине и направлена ​​к оси вращения.

В случае вращения вокруг неподвижной оси твердого тела , которая не пренебрежимо мала по сравнению с радиусом траектории, каждая частица тела описывает равномерное круговое движение с одинаковой угловой скоростью, но со скоростью и ускорением, изменяющимися в зависимости от положения относительно оси.

Формула

Рисунок 1: Векторные соотношения для равномерного кругового движения; вектор Ω , представляющий вращение, перпендикулярен плоскости орбиты.

Для движения по окружности радиусом r длина окружности равна C = 2 πr . Если период одного оборота равен T , угловая скорость вращения, также известная как угловая скорость , ω равна: ω = 2 π T = 2 π f = d θ d t {\displaystyle \omega ={\frac {2\pi }{T}}=2\pi f={\frac {d\theta }{dt}}} и единицы измерения — радианы в секунду.

Скорость объекта, движущегося по окружности, равна: v = 2 π r T = ω r {\displaystyle v={\frac {2\pi r}{T}}=\omega r}

Угол θ , выметаемый за время t, равен: θ = 2 π t T = ω t {\displaystyle \theta =2\pi {\frac {t}{T}}=\omega t}

Угловое ускорение α частицы равно: α = d ω d t {\ displaystyle \alpha ={\frac {d\omega }{dt}}}

В случае равномерного кругового движения α будет равен нулю.

Ускорение из-за изменения направления равно: a c = v 2 r = ω 2 r {\displaystyle a_{c}={\frac {v^{2}}{r}}=\omega ^{2}r}

Центростремительную и центробежную силу также можно найти с помощью ускорения: F c = p ˙ = m ˙ = 0 m a c = m v 2 r {\displaystyle F_{c}={\dot {p}}\mathrel {\overset {{\dot {m}}=0}{=}} ma_{c}={\frac {mv^{2}}{r}}}

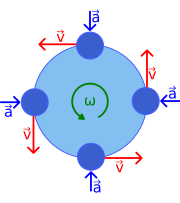
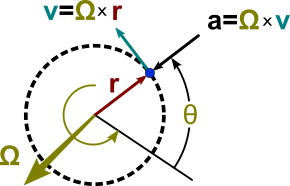
Векторные соотношения показаны на рисунке 1. Ось вращения показана как вектор ω, перпендикулярный плоскости орбиты и имеющий величину ω = dθ / dt . Направление ω выбирается с помощью правила правой руки . При таком соглашении для изображения вращения скорость задается векторным векторным произведением как , которое является вектором, перпендикулярным как ω, так и r ( t ) , касательным к орбите и имеющим величину ω r . Аналогично, ускорение задается как , которое является вектором, перпендикулярным как ω , так и v ( t ) и имеющим величину ω | v | = ω ² r и направленным точно противоположно r ( t ) . ^[1] $${\displaystyle \mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {r} ,}$$ $${\displaystyle \mathbf {a} ={\boldsymbol {\omega }}\times \mathbf {v} ={\boldsymbol {\omega }}\times \left({\boldsymbol {\omega }}\times \mathbf {r} \right),}$$

В простейшем случае скорость, масса и радиус постоянны.

Рассмотрим тело массой один килограмм, движущееся по окружности радиусом один метр с угловой скоростью один радиан в секунду .

• Скорость — 1 метр в секунду.
• Внутреннее ускорение равно 1 метру в квадратную секунду, v ² / r .
• На него действует центростремительная сила в 1 килограмм-метр в квадратную секунду, что составляет 1 ньютон .
• Импульс тела равен 1 кг·м·с − ¹ .
• Момент инерции равен 1 кг·м ² .
• Момент импульса равен 1 кг·м ² ·с ⁻¹ .
• Кинетическая энергия составляет 0,5  джоуля .
• Длина окружности орбиты составляет 2π ( ~6,283) метра .
• Период движения составляет 2π секунды  .
• Частота равна ( 2π ) ⁻¹ герц . 

В полярных координатах

Рисунок 4: Полярные координаты для круговой траектории. Слева — единичная окружность, показывающая изменения и в единичных векторах и для небольшого приращения угла . ${\displaystyle \mathbf {d{\hat {\mathbf {u} }}_{R}} }$ ${\displaystyle \mathbf {d{\hat {\mathbf {u} }}_{\theta }} }$ ${\displaystyle \mathbf {{\hat {\mathbf {u} }}_{R}} }$ ${\displaystyle \mathbf {{\hat {\mathbf {u} }}_{\theta }} }$ ${\displaystyle d\theta }$ ${\displaystyle \theta }$

При круговом движении тело движется по кривой, которую можно описать в полярной системе координат как фиксированное расстояние R от центра орбиты, взятой за начало координат, ориентированное под углом θ ( t ) от некоторого опорного направления. См. рисунок 4. Вектор смещения — это радиальный вектор от начала координат до местоположения частицы: где — единичный вектор, параллельный радиус-вектору в момент времени t и направленный от начала координат. Удобно также ввести единичный вектор, ортогональный к , а именно . Принято ориентироваться так, чтобы он указывал в направлении движения по орбите. ${\displaystyle \mathbf {r} }$ $${\displaystyle \mathbf {r} (t)=R{\hat {\mathbf {u} }}_{R}(t)\,,}$$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$

Скорость — это производная смещения по времени: $${\displaystyle \mathbf {v} (t)={\frac {d}{dt}}\mathbf {r} (t)={\frac {dR}{dt}}{\hat {\mathbf {u} }}_{R}(t)+R{\frac {d{\hat {\mathbf {u} }}_{R}}{dt}}\,.}$$

Поскольку радиус окружности постоянен, радиальная составляющая скорости равна нулю. Единичный вектор имеет неизменяемую во времени величину, равную единице, поэтому при изменении времени его кончик всегда лежит на окружности единичного радиуса с углом θ , таким же, как угол . Если смещение частицы вращается на угол dθ за время dt , то же самое происходит и , описывая дугу на единичной окружности величиной dθ . См. единичную окружность слева на рисунке 4. Следовательно: где направление изменения должно быть перпендикулярно (или, другими словами, вдоль ), поскольку любое изменение направления изменило бы размер . Знак положительный, поскольку увеличение dθ подразумевает, что объект и переместился в направлении . Следовательно, скорость становится: ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle \mathbf {r} (t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ $${\displaystyle {\frac {d{\hat {\mathbf {u} }}_{R}}{dt}}={\frac {d\theta }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)\,,}$$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ ${\displaystyle d{\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ $${\displaystyle \mathbf {v} (t)={\frac {d}{dt}}\mathbf {r} (t)=R{\frac {d{\hat {\mathbf {u} }}_{R}}{dt}}=R{\frac {d\theta }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)=R\omega {\hat {\mathbf {u} }}_{\theta }(t)\,.}$$

Ускорение тела также можно разложить на радиальную и тангенциальную составляющие. Ускорение является производной скорости по времени: $${\displaystyle {\begin{aligned}\mathbf {a} (t)&={\frac {d}{dt}}\mathbf {v} (t)={\frac {d}{dt}}\left(R\omega {\hat {\mathbf {u} }}_{\theta }(t)\right)\\&=R\left({\frac {d\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)+\omega {\frac {d{\hat {\mathbf {u} }}_{\theta }}{dt}}\right)\,.\end{aligned}}}$$

Производная по времени находится так же, как и для . Опять же, является единичным вектором, и его кончик описывает единичную окружность с углом, равным π /2 + θ . Следовательно, увеличение угла dθ на подразумевает описание дуги величиной dθ , и так как ортогонален , то имеем: где отрицательный знак необходим для сохранения ортогональности . (В противном случае угол между и уменьшался бы с увеличением dθ .) См. единичную окружность слева на рисунке 4. Следовательно, ускорение равно: ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ ${\displaystyle \mathbf {r} (t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ $${\displaystyle {\frac {d{\hat {\mathbf {u} }}_{\theta }}{dt}}=-{\frac {d\theta }{dt}}{\hat {\mathbf {u} }}_{R}(t)=-\omega {\hat {\mathbf {u} }}_{R}(t)\,,}$$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{\theta }(t)}$ ${\displaystyle {\hat {\mathbf {u} }}_{R}(t)}$ $${\displaystyle {\begin{aligned}\mathbf {a} (t)&=R\left({\frac {d\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)+\omega {\frac {d{\hat {\mathbf {u} }}_{\theta }}{dt}}\right)\\&=R{\frac {d\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)-\omega ^{2}R{\hat {\mathbf {u} }}_{R}(t)\,.\end{aligned}}}$$

Центростремительное ускорение представляет собой радиальную составляющую, которая направлена ​​радиально внутрь: тогда как тангенциальная составляющая изменяет величину скорости: $${\displaystyle \mathbf {a} _{R}(t)=-\omega ^{2}R{\hat {\mathbf {u} }}_{R}(t)\,,}$$ $${\displaystyle \mathbf {a} _{\theta }(t)=R{\frac {d\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)={\frac {dR\omega }{dt}}{\hat {\mathbf {u} }}_{\theta }(t)={\frac {d\left|\mathbf {v} (t)\right|}{dt}}{\hat {\mathbf {u} }}_{\theta }(t)\,.}$$

Использование комплексных чисел

Круговое движение можно описать с помощью комплексных чисел . Пусть ось x будет действительной осью, а ось — мнимой осью. Тогда положение тела можно задать как , комплексный «вектор»: где i — мнимая единица , а — аргумент комплексного числа как функции времени t . ${\displaystyle y}$ ${\displaystyle z}$ $${\displaystyle z=x+iy=R\left(\cos[\theta (t)]+i\sin[\theta (t)]\right)=Re^{i\theta (t)}\,,}$$ ${\displaystyle \theta (t)}$

Поскольку радиус постоянен: где точка обозначает дифференциацию по времени. $${\displaystyle {\dot {R}}={\ddot {R}}=0\,,}$$

При таком обозначении скорость становится: а ускорение становится: $${\displaystyle v={\dot {z}}={\frac {d}{dt}}\left(Re^{i\theta [t]}\right)=R{\frac {d}{dt}}\left(e^{i\theta [t]}\right)=Re^{i\theta (t)}{\frac {d}{dt}}\left(i\theta [t]\right)=iR{\dot {\theta }}(t)e^{i\theta (t)}=i\omega Re^{i\theta (t)}=i\omega z}$$ $${\displaystyle {\begin{aligned}a&={\dot {v}}=i{\dot {\omega }}z+i\omega {\dot {z}}=\left(i{\dot {\omega }}-\omega ^{2}\right)z\\&=\left(i{\dot {\omega }}-\omega ^{2}\right)Re^{i\theta (t)}\\&=-\omega ^{2}Re^{i\theta (t)}+{\dot {\omega }}e^{i{\frac {\pi }{2}}}Re^{i\theta (t)}\,.\end{aligned}}}$$

Первый член противоположен по направлению вектору смещения, а второй перпендикулярен ему, как и в предыдущих результатах.

Скорость

Рисунок 1 иллюстрирует векторы скорости и ускорения для равномерного движения в четырех различных точках орбиты. Поскольку скорость v касается круговой траектории, никакие две скорости не указывают в одном и том же направлении. Хотя объект имеет постоянную скорость , его направление всегда меняется. Это изменение скорости вызвано ускорением a , величина которого (как и у скорости) сохраняется постоянной, но направление которого также всегда меняется. Ускорение направлено радиально внутрь ( центростремительно ) и перпендикулярно скорости. Это ускорение известно как центростремительное ускорение.

Для траектории радиуса r , когда угол θ выметается, расстояние, пройденное по периферии орбиты, равно s = rθ . Следовательно, скорость движения по орбите равна , где угловая скорость вращения равна ω . (Путем перестановки, ω = v / r .) Таким образом, v является константой, и вектор скорости v также вращается с постоянной величиной v , с той же угловой скоростью ω . $${\displaystyle v=r{\frac {d\theta }{dt}}=r\omega ,}$$

Релятивистское круговое движение

В этом случае вектор три-ускорения перпендикулярен вектору три-скорости, а квадрат собственного ускорения, выраженный как скалярный инвариант, одинаковый во всех системах отсчета, становится выражением для кругового движения, или, взяв положительный квадратный корень и используя три-ускорение, приходим к собственному ускорению для кругового движения: $${\displaystyle \mathbf {u} \cdot \mathbf {a} =0.}$$ $${\displaystyle \alpha ^{2}=\gamma ^{4}a^{2}+\gamma ^{6}\left(\mathbf {u} \cdot \mathbf {a} \right)^{2},}$$ $${\displaystyle \alpha ^{2}=\gamma ^{4}a^{2}.}$$ $${\displaystyle \alpha =\gamma ^{2}{\frac {v^{2}}{r}}.}$$

Ускорение

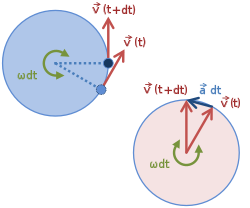
Левый круг на рисунке 2 — это орбита, показывающая векторы скорости в два соседних момента времени. Справа эти две скорости перемещаются так, что их хвосты совпадают. Поскольку скорость постоянна, векторы скорости справа описывают окружность с течением времени. Для угла стреловидности dθ = ω dt изменение v — это вектор, перпендикулярный v и имеющий величину v dθ , что, в свою очередь, означает, что величина ускорения определяется выражением $${\displaystyle a_{c}=v{\frac {d\theta }{dt}}=v\omega ={\frac {v^{2}}{r}}}$$

Неравномерное круговое движение

При неравномерном круговом движении объект движется по круговой траектории с переменной скоростью . Поскольку скорость меняется, в дополнение к нормальному ускорению возникает тангенциальное ускорение .

При неравномерном круговом движении чистое ускорение (a) направлено вдоль направления Δ v , которое направлено внутрь круга, но не проходит через его центр (см. рисунок). Чистое ускорение можно разложить на две составляющие: тангенциальное ускорение и нормальное ускорение, также известное как центростремительное или радиальное ускорение. В отличие от тангенциального ускорения, центростремительное ускорение присутствует как при равномерном, так и при неравномерном круговом движении.

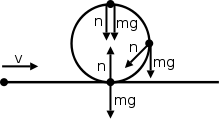
При неравномерном круговом движении нормальная сила не всегда направлена ​​в противоположном направлении от веса . Вот пример с объектом, движущимся по прямой траектории, а затем снова делающим петлю, возвращаясь к прямой траектории.

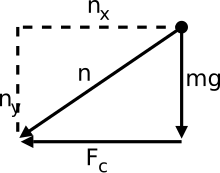
На этой диаграмме показана нормальная сила, направленная в других направлениях, а не противоположно силе веса. Нормальная сила на самом деле является суммой радиальной и тангенциальной сил. Компонент силы веса отвечает за тангенциальную силу здесь (мы пренебрегли силой трения). Радиальная сила (центростремительная сила) обусловлена ​​изменением направления скорости, как обсуждалось ранее.

При неравномерном круговом движении нормальная сила и вес могут быть направлены в одном направлении. Обе силы могут быть направлены вниз, но объект останется на круговой траектории, не падая прямо вниз. Сначала давайте посмотрим, почему нормальная сила может быть направлена ​​вниз в первую очередь. На первой диаграмме предположим, что объект — это человек, сидящий внутри плоскости, две силы направлены вниз только тогда, когда он достигает вершины круга. Причина этого в том, что нормальная сила является суммой тангенциальной силы и центростремительной силы. Тангенциальная сила равна нулю наверху (так как работа не выполняется, когда движение перпендикулярно направлению приложенной силы. Здесь сила веса перпендикулярна направлению движения объекта в верхней части круга), а центростремительная сила направлена ​​вниз, поэтому нормальная сила также будет направлена ​​вниз. С логической точки зрения человек, который движется в плоскости, будет перевернут вверх ногами наверху круга. В этот момент сиденье человека фактически давит на человека, что и является нормальной силой.

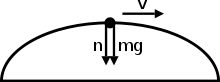
Причина, по которой объект не падает, когда на него действуют только направленные вниз силы, проста. Подумайте о том, что удерживает объект в воздухе после того, как его бросили. Как только объект брошен в воздух, на него действует только направленная вниз сила земного притяжения. Это не значит, что как только объект брошен в воздух, он мгновенно упадет. То, что удерживает объект в воздухе, — это его скорость . Первый из законов движения Ньютона гласит, что инерция объекта удерживает его в движении, и поскольку объект в воздухе имеет скорость, он будет стремиться продолжать двигаться в этом направлении.

Изменяющаяся угловая скорость для объекта, движущегося по круговой траектории, может быть достигнута также, если вращающееся тело не имеет однородного распределения массы. Для неоднородных объектов необходимо подходить к задаче, как в ^{[2] .}

Можно вывести формулы скорости, ускорения и рывка, предполагая, что все переменные зависят от : ${\displaystyle t}$ $${\displaystyle \mathbf {r} =R\mathbf {u} _{R}}$$ $${\displaystyle {\dot {\mathbf {u} }}_{R}=\omega \mathbf {u} _{\theta }}$$ $${\displaystyle {\dot {\mathbf {u} }}_{\theta }=-\omega \mathbf {u} _{R}}$$ $${\displaystyle \mathbf {v} ={\frac {d}{dt}}\mathbf {r} ={\dot {\mathbf {r} }}={\dot {R}}\mathbf {u} _{R}+R\omega \mathbf {u} _{\theta }}$$ $${\displaystyle \mathbf {a} ={\frac {d}{dt}}\mathbf {v} ={\dot {\mathbf {v} }}={\ddot {R}}\mathbf {u} _{R}+\left({\dot {R}}\omega \mathbf {u} _{\theta }+{\dot {R}}\omega \mathbf {u} _{\theta }\right)+R{\dot {\omega }}\mathbf {u} _{\theta }-R\omega ^{2}\mathbf {u} _{R}}$$

$${\displaystyle \mathbf {j} ={\frac {d}{dt}}\mathbf {a} ={\dot {\mathbf {a} }}={\dot {\ddot {R}}}\mathbf {u} _{R}+{\ddot {R}}\omega \mathbf {u} _{\theta }+\left(2{\ddot {R}}\omega \mathbf {u} _{\theta }+2{\dot {R}}{\dot {\omega }}\mathbf {u} _{\theta }-2{\dot {R}}\omega ^{2}\mathbf {u} _{R}\right)+{\dot {R}}{\dot {\omega }}\mathbf {u} _{\theta }+R{\ddot {\omega }}\mathbf {u} _{\theta }-R{\dot {\omega }}\omega \mathbf {u} _{R}-{\dot {R}}\omega ^{2}\mathbf {u} _{R}-R2{\dot {\omega }}\omega \mathbf {u} _{R}-R\omega ^{3}\mathbf {u} _{\theta }}$$

$${\displaystyle \mathbf {j} =\left({\dot {\ddot {R}}}-3{\dot {R}}\omega ^{2}-3R{\dot {\omega }}\omega \right)\mathbf {u} _{R}+\left(3{\ddot {R}}\omega +3{\dot {R}}{\dot {\omega }}+R{\ddot {\omega }}-R\omega ^{3}\right)\mathbf {u} _{\theta }}$$

Дальнейшие преобразования могут включать и соответствующие производные: ${\displaystyle curvature=c={\frac {1}{R}},\omega ={\frac {v}{R}}=vc}$ $${\displaystyle {\begin{aligned}{\dot {R}}&=-{\frac {\dot {c}}{c^{2}}}\\{\ddot {R}}&={\frac {2\left({\dot {c}}\right)^{2}}{c^{3}}}-{\frac {\ddot {c}}{c^{2}}}\\{\dot {\omega }}&={\frac {{\dot {v}}R-{\dot {R}}v}{R^{2}}}={\dot {v}}c+v{\dot {c}}\\\end{aligned}}}$$

Приложения

Решение задач, связанных с неравномерным круговым движением, включает силовой анализ. При равномерном круговом движении единственной силой, действующей на объект, движущийся по окружности, является центростремительная сила. При неравномерном круговом движении на объект действуют дополнительные силы из-за ненулевого тангенциального ускорения. Хотя на объект действуют дополнительные силы, сумма всех сил, действующих на объект, должна быть равна центростремительной силе. $${\displaystyle {\begin{aligned}F_{\text{net}}&=ma\\&=ma_{r}\\&={\frac {mv^{2}}{r}}\\&=F_{c}\end{aligned}}}$$

Радиальное ускорение используется при расчете общей силы. Тангенциальное ускорение не используется при расчете общей силы, поскольку оно не отвечает за удержание объекта на круговой траектории. Единственное ускорение, отвечающее за поддержание движения объекта по окружности, — это радиальное ускорение. Поскольку сумма всех сил — это центростремительная сила, внесение центростремительной силы в диаграмму свободного тела не является необходимым и обычно не рекомендуется.

Используя , мы можем нарисовать диаграммы свободного тела, чтобы перечислить все силы, действующие на объект, а затем установить его равным . После этого мы можем решить для всего, что неизвестно (это может быть масса, скорость, радиус кривизны, коэффициент трения, нормальная сила и т. д.). Например, изображение выше, показывающее объект в верхней части полукруга, будет выражено как . ${\displaystyle F_{\text{net}}=F_{c}}$ ${\displaystyle F_{c}}$ ${\displaystyle F_{c}=n+mg}$

При равномерном круговом движении полное ускорение объекта на круговой траектории равно радиальному ускорению. Из-за наличия тангенциального ускорения в неравномерном круговом движении это больше не верно. Чтобы найти полное ускорение объекта на неравномерном круговом движении, найдите векторную сумму тангенциального ускорения и радиального ускорения. $${\displaystyle {\sqrt {a_{r}^{2}+a_{t}^{2}}}=a}$$

Радиальное ускорение по-прежнему равно . Тангенциальное ускорение — это просто производная скорости в любой заданной точке: . Эта корневая сумма квадратов отдельных радиальных и тангенциальных ускорений верна только для кругового движения; для общего движения в плоскости с полярными координатами член Кориолиса следует добавить к , тогда как радиальное ускорение становится . ${\textstyle {\frac {v^{2}}{r}}}$ ${\textstyle a_{t}={\frac {dv}{dt}}}$ ${\displaystyle (r,\theta )}$ ${\textstyle a_{c}=2\left({\frac {dr}{dt}}\right)\left({\frac {d\theta }{dt}}\right)}$ ${\displaystyle a_{t}}$ ${\textstyle a_{r}={\frac {-v^{2}}{r}}+{\frac {d^{2}r}{dt^{2}}}}$

Смотрите также

• Угловой момент импульса
• Уравнения движения для кругового движения
• Производная по времени § Пример: круговое движение
• Фиктивная сила
• Геостационарная орбита
• Геосинхронная орбита
• Маятник (механика)
• Реактивная центробежная сила
• Возвратно-поступательное движение
• Простое гармоническое движение § Равномерное круговое движение
• Праща (оружие)

Ссылки

1. Кнудсен, Йенс М.; Хьорт, Пол Г. (2000). Элементы ньютоновской механики: включая нелинейную динамику (3-е изд.). Springer. стр. 96. ISBN 3-540-67652-X.
2. Gomez, RW; Hernandez-Gomez, JJ; Marquina, V (25 июля 2012 г.). "Прыгающий цилиндр на наклонной плоскости". Eur. J. Phys . 33 (5). IOP: 1359–1365. arXiv : 1204.0600 . Bibcode : 2012EJPh...33.1359G. doi : 10.1088/0143-0807/33/5/1359. S2CID  55442794. Получено 25 апреля 2016 г.

Внешние ссылки

• Physclips: Механика с анимациями и видеоклипами от Университета Нового Южного Уэльса
• Круговое движение – глава из онлайн-учебника «Механика» Бенджамина Кроуэлла (2019)
• Лекция по круговому движению – видеолекция по КМ
• [1] – онлайн-учебник с различным анализом кругового движения