
В математике седловая точка или точка минимакса [1] — это точка на поверхности графика функции , где наклоны (производные) в ортогональных направлениях все равны нулю ( критическая точка ), но которая не является локальным экстремумом функции. [2] Примером седловой точки является ситуация, когда есть критическая точка с относительным минимумом вдоль одного осевого направления (между пиками) и с относительным максимумом вдоль пересекающей оси. Однако седловая точка не обязательно должна быть в такой форме. Например, функция имеет критическую точку в , которая является седловой точкой, поскольку она не является ни относительным максимумом, ни относительным минимумом, но она не имеет относительного максимума или относительного минимума в -направлении.

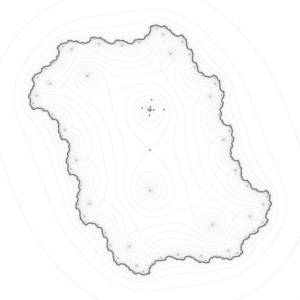
Название происходит от того факта, что прототипическим примером в двух измерениях является поверхность , которая изгибается вверх в одном направлении и изгибается вниз в другом направлении, напоминая седло для верховой езды . С точки зрения контурных линий , седловая точка в двух измерениях дает контурную карту с парой линий, пересекающихся в этой точке. Такие пересечения редки на реальных картах боеприпасов, поскольку высота седловой точки вряд ли будет совпадать с целыми кратными, используемыми в таких картах. Вместо этого седловая точка отображается как пустое пространство в середине четырех наборов контурных линий, которые приближаются к ней и отклоняются от нее. Для базовой седловой точки эти наборы встречаются парами, с противолежащей высокой парой и противолежащей низкой парой, расположенными в ортогональных направлениях. Критические контурные линии, как правило, не обязательно должны пересекаться ортогонально.
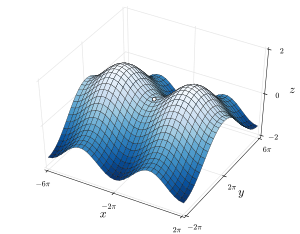
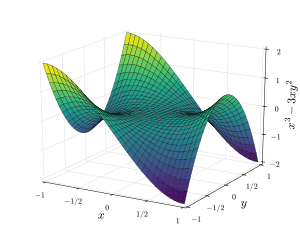
Простым критерием проверки того, является ли заданная стационарная точка действительной функции F ( x , y ) двух действительных переменных седловой точкой, является вычисление матрицы Гессе функции в этой точке: если гессиан неопределен , то эта точка является седловой точкой. Например, матрица Гессе функции в стационарной точке — это матрица
которая неопределенна. Следовательно, эта точка является седловой. Этот критерий дает только достаточное условие. Например, точка является седловой точкой для функции , но матрица Гессе этой функции в начале координат является нулевой матрицей , которая не является неопределенной.
В самых общих чертах, седловая точка для гладкой функции ( графиком которой является кривая , поверхность или гиперповерхность ) — это стационарная точка, такая что кривая/поверхность и т. д. в окрестности этой точки не находится полностью по какую-либо сторону касательного пространства в этой точке.

В области одного измерения седловая точка — это точка , которая является как стационарной точкой, так и точкой перегиба . Поскольку это точка перегиба, она не является локальным экстремумом .


Седловая поверхность — гладкая поверхность, содержащая одну или несколько седловых точек.
Классическими примерами двумерных седловых поверхностей в евклидовом пространстве являются поверхности второго порядка, гиперболический параболоид (который часто называют « седловой поверхностью» или «стандартной седловой поверхностью») и гиперболоид одного листа . Картофельные чипсы Pringles или хрустящие чипсы являются повседневным примером формы гиперболического параболоида.
Седловые поверхности имеют отрицательную гауссову кривизну , что отличает их от выпуклых/эллиптических поверхностей, которые имеют положительную гауссову кривизну. Классическая седловая поверхность третьего порядка — обезьянье седло . [3]
В игре двух игроков с нулевой суммой, определенной на непрерывном пространстве, точка равновесия является седловой точкой.
Для линейной автономной системы второго порядка критическая точка является седловой, если характеристическое уравнение имеет одно положительное и одно отрицательное действительное собственное значение . [4]
При оптимизации с ограничениями типа равенства условия первого порядка описывают седловую точку лагранжиана .
В динамических системах , если динамика задана дифференцируемым отображением f, то точка является гиперболической тогда и только тогда, когда дифференциал ƒ n (где n — период точки) не имеет собственного значения на (комплексной) единичной окружности при вычислении в точке. Тогда седловая точка является гиперболической периодической точкой , устойчивые и неустойчивые многообразия которой имеют размерность , отличную от нуля.
Седловая точка матрицы — это элемент, который одновременно является наибольшим элементом в своем столбце и наименьшим элементом в своей строке.