
В геометрии объект обладает симметрией , если существует операция или преобразование (например, перенос , масштабирование , вращение или отражение ), которое отображает фигуру/объект на себя (т. е. объект обладает инвариантностью относительно преобразования). [1] Таким образом, симметрию можно рассматривать как иммунитет к изменениям. [2] Например, круг, повернутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг, поскольку все точки до и после преобразования будут неразличимы. Таким образом, говорят, что круг симметричен относительно вращения или имеет вращательную симметрию . Если изометрия является отражением плоской фигуры относительно прямой, то говорят, что фигура имеет отражательную симметрию или симметрию относительно линии ; [3] также возможно, что фигура/объект имеет более одной оси симметрии. [4]
Типы симметрий, которые возможны для геометрического объекта, зависят от набора доступных геометрических преобразований и от того, какие свойства объекта должны оставаться неизменными после преобразования. Поскольку композиция двух преобразований также является преобразованием, и каждое преобразование имеет, по определению, обратное преобразование, которое отменяет его, набор преобразований, при которых объект симметричен, образует математическую группу , группу симметрии объекта. [5]
Наиболее распространенная группа преобразований, применяемых к объектам, называется евклидовой группой « изометрий », которые являются сохраняющими расстояние преобразованиями в пространстве, обычно называемыми двумерными или трехмерными (т. е. в плоской геометрии или стереометрии евклидовых пространств ). Эти изометрии состоят из отражений , вращений , трансляций и комбинаций этих основных операций. [6] При изометрическом преобразовании геометрический объект называется симметричным, если после преобразования объект неотличим от объекта до преобразования. [7] Геометрический объект обычно симметричен только относительно подмножества или « подгруппы » всех изометрий. Ниже описаны виды подгрупп изометрий, за которыми следуют другие виды групп преобразований и типы инвариантности объектов, возможные в геометрии.
По теореме Картана–Дьедонне ортогональное преобразование в n -мерном пространстве может быть представлено композицией не более чем n отражений.
Зеркальная симметрия, линейная симметрия, зеркальная симметрия, симметрия зеркального отображения или двусторонняя симметрия — это симметрия относительно отражения. [8]
В одном измерении есть точка симметрии, относительно которой происходит отражение; в двух измерениях есть ось симметрии (она же линия симметрии), а в трех измерениях есть плоскость симметрии. [3] [9] Объект или фигура, для которых каждая точка имеет взаимно-однозначное отображение на другую, равноудаленную от и на противоположных сторонах общей плоскости, называется зеркально-симметричным (подробнее см. зеркальное отображение ).
Ось симметрии двумерной фигуры — это линия, такая, что если построить перпендикуляр , то любые две точки, лежащие на перпендикуляре на равном расстоянии от оси симметрии, идентичны. Другой способ думать об этом — если бы фигуру сложили пополам по оси, две половины были бы идентичны как зеркальные отражения друг друга. Например, квадрат имеет четыре оси симметрии, потому что есть четыре различных способа сложить его и сделать так, чтобы края совпадали друг с другом. Другим примером может служить круг , который имеет бесконечно много осей симметрии, проходящих через его центр по той же причине. [10]
Если букву T отразить вдоль вертикальной оси, она будет выглядеть так же. Иногда это называют вертикальной симметрией. Таким образом, можно однозначно описать это явление, сказав, что «T имеет вертикальную ось симметрии» или что «T имеет лево-правую симметрию».
Треугольники с зеркальной симметрией являются равнобедренными , четырехугольники с этой симметрией являются воздушными змеями и равнобедренными трапециями . [11]
Для каждой линии или плоскости отражения группа симметрии изоморфна C s ( см. точечные группы в трех измерениях для получения дополнительной информации), одному из трех типов второго порядка ( инволюции ), следовательно, алгебраически изоморфна C 2 . Фундаментальная область — это полуплоскость или полупространство . [12]

Симметрию отражения можно обобщить на другие изометрии m - мерного пространства, которые являются инволюциями , например:
в определенной системе декартовых координат . Это отражает пространство вдоль ( m − k ) -мерного аффинного подпространства . [13] Если k = m , то такое преобразование известно как точечное отражение или инверсия относительно точки . На плоскости ( m = 2) точечное отражение совпадает с вращением на пол- оборота (180°); см. ниже. Антиподальная симметрия — это альтернативное название для симметрии точечного отражения относительно начала координат. [14]
Такое «отражение» сохраняет ориентацию тогда и только тогда, когда k — четное число. [15] Это подразумевает, что при m = 3 (а также при других нечетных m ) точечное отражение изменяет ориентацию пространства, подобно симметрии зеркального отображения. Это объясняет, почему в физике термин P- симметрия (P обозначает четность ) используется как для точечного отражения, так и для зеркальной симметрии. Поскольку точечное отражение в трех измерениях изменяет левую систему координат в правую , симметрия относительно точечного отражения также называется лево-правой симметрией. [16]

Вращательная симметрия — это симметрия относительно некоторых или всех вращений в m -мерном евклидовом пространстве. Вращения — это прямые изометрии , которые являются изометриями, сохраняющими ориентацию . [17] Следовательно, группа симметрии вращательной симметрии является подгруппой специальной евклидовой группы E + ( m ) .
Симметрия относительно всех вращений вокруг всех точек подразумевает трансляционную симметрию относительно всех трансляций (потому что трансляции являются композициями вращений вокруг различных точек), [18] а группа симметрии — это все E + ( m ). Это не применимо к объектам, поскольку делает пространство однородным, но может применяться к физическим законам.
Для симметрии относительно вращений вокруг точки можно взять эту точку за начало координат. Эти вращения образуют специальную ортогональную группу SO( m ), которая может быть представлена группой ортогональных матриц m × m с определителем 1. Для m = 3 это группа вращений SO(3) . [19]
Выражаясь немного по-другому, группа вращения объекта — это группа симметрии внутри E + ( m ), группа жестких движений; [20] то есть пересечение полной группы симметрии и группы жестких движений. Для хиральных объектов это то же самое, что и полная группа симметрии.
Законы физики являются SO(3)-инвариантными, если они не различают различные направления в пространстве. Из-за теоремы Нётер вращательная симметрия физической системы эквивалентна закону сохранения углового момента . [21] Подробнее см. вращательная инвариантность .

Трансляционная симметрия оставляет объект инвариантным при дискретной или непрерывной группе трансляций . [22] Иллюстрация справа показывает четыре конгруэнтных следа, созданных трансляциями вдоль стрелки. Если бы линия следов простиралась до бесконечности в обоих направлениях, то они имели бы дискретную трансляционную симметрию; любая трансляция, которая отображает один след на другой, оставила бы всю линию неизменной.

В 2D симметрия скользящего отражения (также называемая симметрией скользящей плоскости в 3D и трансфлекцией в целом) означает, что отражение относительно линии или плоскости в сочетании с переносом вдоль линии или плоскости приводит к одному и тому же объекту (например, в случае следов). [2] [23] Композиция двух скользящих отражений приводит к симметрии переноса с удвоенным вектором переноса. Группа симметрии, включающая скользящие отражения и связанные с ними переносы, является группой фриза p11g и изоморфна бесконечной циклической группе Z.
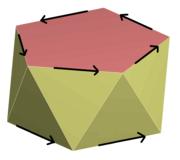
В 3D вращательное отражение , роторное отражение или неправильное вращение представляет собой вращение вокруг оси в сочетании с отражением в плоскости, перпендикулярной этой оси. [24] Группы симметрии, связанные с роторными отражениями, включают:
Для получения дополнительной информации см. точечные группы в трех измерениях .
В 3D-геометрии и выше винтовая ось (или вращательное перемещение) представляет собой комбинацию вращения и перемещения вдоль оси вращения. [25]
Спиральная симметрия — это вид симметрии, наблюдаемый в повседневных предметах, таких как пружины , игрушки- пружинки , сверла и шнеки . Концепцию спиральной симметрии можно визуализировать как трассировку в трехмерном пространстве, которая получается в результате вращения объекта с постоянной угловой скоростью при одновременном перемещении с постоянной линейной скоростью вдоль его оси вращения. В любой момент времени эти два движения объединяются, чтобы дать угол намотки , который помогает определить свойства трассируемой спирали. [26] Когда трассируемый объект вращается быстро и перемещается медленно, угол намотки будет близок к 0°. И наоборот, если объект вращается медленно и перемещается быстро, угол намотки будет приближаться к 90°.

На основе взаимодействия угла навивки и трансляционной симметрии вдоль оси можно выделить три основных класса спиральной симметрии:



В 4D симметрия двойного вращения может быть создана как композиция двух ортогональных вращений. [29] Она похожа на ось винта 3D, которая является композицией вращения и ортогонального переноса.
Более широкое определение геометрической симметрии допускает операции из более крупной группы, чем евклидова группа изометрий. Примерами более крупных групп геометрической симметрии являются:
В программе Эрлангена Феликса Клейна каждая возможная группа симметрий определяет геометрию, в которой объекты, связанные членом группы симметрии, считаются эквивалентными. [32] Например, группа Евклида определяет геометрию Евклида , тогда как группа преобразований Мёбиуса определяет проективную геометрию .

Масштабная симметрия означает, что если объект увеличивается или уменьшается в размере, новый объект имеет те же свойства, что и исходный. [33] Это самоподобие наблюдается во многих природных структурах, таких как кучевые облака, молнии, папоротники и береговые линии, в широком диапазоне масштабов. Оно, как правило, не встречается в гравитационно связанных структурах, например, в форме ног слона и мыши ( так называемое аллометрическое масштабирование ). Аналогично, если бы мягкая восковая свеча была увеличена до размера высокого дерева, она бы немедленно рухнула под собственным весом.
Более тонкая форма масштабной симметрии демонстрируется фракталами . По замыслу Бенуа Мандельброта , фракталы — это математическая концепция, в которой структура сложной формы выглядит одинаково при любой степени увеличения , [34] хорошо видно в множестве Мандельброта . Берег — пример естественного фрактала, поскольку он сохраняет схожую сложность на каждом уровне, от вида со спутника до микроскопического исследования того, как вода плещется об отдельные песчинки. Ветвление деревьев, которое позволяет небольшим веточкам заменять целые деревья в диорамах , — еще один пример.
Поскольку фракталы могут создавать видимость узоров в природе , они обладают красотой и узнаваемостью, которые обычно не встречаются в математически сгенерированных функциях. Фракталы также нашли свое место в компьютерных эффектах фильмов , где их способность создавать сложные кривые с фрактальной симметрией приводит к более реалистичным виртуальным мирам .
С каждой геометрией Феликс Клейн связал базовую группу симметрий . Таким образом, иерархия геометрий математически представлена как иерархия этих групп и иерархия их инвариантов . Например, длины, углы и площади сохраняются относительно евклидовой группы симметрий, в то время как только структура инцидентности и двойное отношение сохраняются при самых общих проективных преобразованиях . Понятие параллельности , которое сохраняется в аффинной геометрии , не имеет смысла в проективной геометрии . Затем, абстрагируя базовые группы симметрий от геометрий, отношения между ними могут быть восстановлены на уровне группы. Поскольку группа аффинной геометрии является подгруппой группы проективной геометрии, любое понятие, инвариантное в проективной геометрии, априори имеет смысл в аффинной геометрии; но не наоборот. Если вы добавите требуемые симметрии, у вас будет более мощная теория, но меньше концепций и теорем (которые будут более глубокими и общими).
Уильям Терстон ввел похожую версию симметрий в геометрии. Модельная геометрия — это односвязное гладкое многообразие X вместе с транзитивным действием группы Ли G на X с компактными стабилизаторами. Группу Ли можно рассматривать как группу симметрий геометрии.
Модельная геометрия называется максимальной, если G максимальна среди групп, действующих гладко и транзитивно на X с компактными стабилизаторами, т. е. если она является максимальной группой симметрий. Иногда это условие включают в определение модельной геометрии.
Геометрическая структура на многообразии M — это диффеоморфизм из M в X /Γ для некоторой модельной геометрии X , где Γ — дискретная подгруппа G , действующая свободно на X. Если данное многообразие допускает геометрическую структуру, то оно допускает и такую, модель которой максимальна.
Трехмерная модельная геометрия X имеет отношение к гипотезе геометризации, если она максимальна и если существует по крайней мере одно компактное многообразие с геометрической структурой, смоделированной на X. Терстон классифицировал 8 модельных геометрий, удовлетворяющих этим условиям; они перечислены ниже и иногда называются геометриями Терстона . (Существует также несчетное множество модельных геометрий без компактных факторов.)