В геометрии , кантелляция — это усечение 2-го порядка в любом измерении, которое скашивает правильный многогранник на его ребрах и вершинах , создавая новую грань на месте каждого ребра и каждой вершины. Кантелляция также применяется к правильным мозаикам и сотам . Кантелляция многогранника также является ректификацией его ректификации .
Сокращение (для многогранников и мозаик) Алисия Буль Стотт также называет расширением : оно соответствует перемещению граней правильной формы от центра и заполнению новой грани в зазоре для каждого открытого ребра и каждой открытой вершины.
Скошенный многогранник представляется расширенным символом Шлефли t 0,2 { p , q ,...} или r или rr { p , q ,...}.
Для многогранников кантелляция обеспечивает прямую последовательность от правильного многогранника к его двойственному .
Пример: последовательность кантеллирования между кубом и октаэдром:
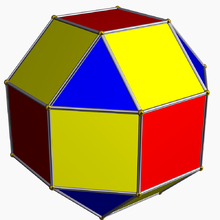
Пример: кубооктаэдр — это усеченный тетраэдр .
Для многогранников более высокой размерности кантелляция обеспечивает прямую последовательность от правильного многогранника к его двойному выпрямлению .