Вязкость

Сопротивление жидкости сдвиговой деформации

Вязкость жидкости является мерой ее сопротивления деформации с заданной скоростью. ^[1] Для жидкостей она соответствует неформальному понятию «густота»: например, сироп имеет более высокую вязкость, чем вода . ^{[2] Вязкость определяется с} научной точки зрения как сила, умноженная на время, деленное на площадь. Таким образом, ее единицами СИ являются ньютон-секунды на квадратный метр или паскаль-секунды. ^[1]

Вязкость количественно определяет внутреннюю силу трения между соседними слоями жидкости, которые находятся в относительном движении. ^[1] Например, когда вязкая жидкость продавливается через трубку, она течет быстрее вблизи центральной линии трубки, чем вблизи ее стенок. ^[3] Эксперименты показывают, что для поддержания потока необходимо некоторое напряжение (такое как разность давлений между двумя концами трубки). Это происходит потому, что требуется сила для преодоления трения между слоями жидкости, которые находятся в относительном движении. Для трубки с постоянной скоростью потока величина компенсирующей силы пропорциональна вязкости жидкости.

В общем случае вязкость зависит от состояния жидкости, например, от ее температуры, давления и скорости деформации. Однако зависимость от некоторых из этих свойств в определенных случаях незначительна. Например, вязкость ньютоновской жидкости не сильно зависит от скорости деформации.

Нулевая вязкость (отсутствие сопротивления сдвиговому напряжению ) наблюдается только при очень низких температурах в сверхтекучих жидкостях ; в противном случае второй закон термодинамики требует, чтобы все жидкости имели положительную вязкость. ^{[4] [5]} Жидкость, имеющая нулевую вязкость (невязкая), называется идеальной или невязкой .

Для вязкости неньютоновских жидкостей существуют псевдопластичные , пластичные и дилатантные течения, которые не зависят от времени, а также тиксотропные и реопектические течения, которые зависят от времени.

Этимология

Слово «вязкость» происходит от латинского viscum (« омела »). Viscum также называют вязкий клей, получаемый из ягод омелы. ^[6]

Определения

Динамическая вязкость

Иллюстрация плоского течения Куэтта . Поскольку сдвиговому потоку противостоит трение между соседними слоями жидкости (которые находятся в относительном движении), требуется сила для поддержания движения верхней пластины. Относительная величина этой силы является мерой вязкости жидкости.

В общем параллельном потоке напряжение сдвига пропорционально градиенту скорости.

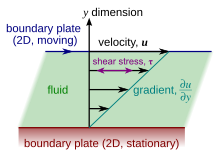
В материаловедении и инженерии часто возникает интерес к пониманию сил или напряжений, участвующих в деформации материала. Например, если бы материал был простой пружиной, ответ был бы дан законом Гука , который гласит, что сила, испытываемая пружиной, пропорциональна расстоянию, смещенному от равновесия. Напряжения, которые можно отнести к деформации материала из некоторого состояния покоя, называются упругими напряжениями. В других материалах присутствуют напряжения, которые можно отнести к скорости деформации с течением времени . Они называются вязкими напряжениями. Например, в жидкости, такой как вода, напряжения, возникающие при сдвиге жидкости, не зависят от расстояния, на которое была сдвинута жидкость; скорее, они зависят от того, как быстро происходит сдвиг.

Вязкость — это свойство материала, которое связывает вязкие напряжения в материале со скоростью изменения деформации (скоростью деформации). Хотя это относится к общим потокам, его легко визуализировать и определить в простом сдвиговом потоке, таком как плоский поток Куэтта .

В потоке Куэтта жидкость оказывается запертой между двумя бесконечно большими пластинами, одна из которых неподвижна, а другая движется параллельно с постоянной скоростью (см. иллюстрацию справа). Если скорость верхней пластины достаточно мала (чтобы избежать турбулентности), то в стационарном состоянии частицы жидкости движутся параллельно ей, и их скорость меняется от нижней к верхней. ^[7] Каждый слой жидкости движется быстрее, чем тот, что находится прямо под ним, и трение между ними приводит к возникновению силы, сопротивляющейся их относительному движению. В частности, жидкость прикладывает к верхней пластине силу в направлении, противоположном ее движению, и равную, но противоположную силу к нижней пластине. Поэтому требуется внешняя сила, чтобы поддерживать движение верхней пластины с постоянной скоростью. ${\displaystyle u}$ ${\displaystyle 0}$ ${\displaystyle u}$

Во многих жидкостях скорость потока, как наблюдается, изменяется линейно от нуля внизу до вершины. Более того, величина силы , действующей на верхнюю пластину, оказывается пропорциональной скорости и площади каждой пластины и обратно пропорциональной их разделению : ${\displaystyle u}$ ${\displaystyle F}$ ${\displaystyle u}$ ${\displaystyle A}$ ${\displaystyle y}$

${\displaystyle F=\mu A{\frac {u}{y}}.}$

Коэффициент пропорциональности — это динамическая вязкость жидкости, часто просто называемая вязкостью . Она обозначается греческой буквой мю ( μ ). Динамическая вязкость имеет размерность , что приводит к единицам СИ и производным единицам : ${\displaystyle \mathrm {(mass/length)/time} }$

${\displaystyle [\mu ]={\frac {\rm {kg}}{\rm {m{\cdot }s}}}={\frac {\rm {N}}{\rm {m^{2}}}}{\cdot }{\rm {s}}={\rm {Pa{\cdot }s}}=}$ давление, умноженное на время , энергия на единицу объема, умноженная на время. ${\displaystyle =}$

Вышеупомянутое отношение называется скоростью деформации сдвига или скоростью сдвига и является производной скорости жидкости в направлении, параллельном вектору нормали пластин (см. иллюстрации справа). Если скорость не изменяется линейно с , то соответствующее обобщение имеет вид: ${\displaystyle u/y}$ ${\displaystyle y}$

${\displaystyle \tau =\mu {\frac {\partial u}{\partial y}},}$

где , а — локальная скорость сдвига. Это выражение называется законом вязкости Ньютона . В сдвиговых потоках с плоской симметрией это то, что определяет . Это частный случай общего определения вязкости (см. ниже), которое может быть выражено в форме, свободной от координат. ${\displaystyle \tau =F/A}$ ${\displaystyle \partial u/\partial y}$ ${\displaystyle \mu }$

Использование греческой буквы мю ( ) для динамической вязкости (иногда также называемой абсолютной вязкостью ) распространено среди инженеров -механиков и химиков , а также математиков и физиков. ^{[8] [9] [10]} Однако греческая буква эта ( ) также используется химиками, физиками и ИЮПАК . ^[11] Вязкость иногда также называют сдвиговой вязкостью . Однако, по крайней мере, один автор не рекомендует использовать эту терминологию, отмечая, что может появляться в несдвиговых потоках в дополнение к сдвиговым потокам. ^[12] ${\displaystyle \mu }$ ${\displaystyle \eta }$ ${\displaystyle \mu }$ ${\displaystyle \mu }$

Кинематическая вязкость

В динамике жидкости иногда более целесообразно работать с термином кинематической вязкости (иногда также называемой коэффициентом диффузии импульса ), определяемой как отношение динамической вязкости ( μ ) к плотности жидкости ( ρ ). Обычно она обозначается греческой буквой nu ( ν ):

${\displaystyle \nu ={\frac {\mu }{\rho }},}$

и имеет размерности , следовательно, в результате получаются единицы СИ и производные единицы : ${\displaystyle \mathrm {(length)^{2}/time} }$

${\displaystyle [\nu ]=\mathrm {\frac {m^{2}}{s}} =\mathrm {{\frac {N{\cdot }m}{kg}}{\cdot }s} =\mathrm {{\frac {J}{kg}}{\cdot }s} =}$ удельная энергия , умноженная на время энергия на единицу массы, умноженная на время. ${\displaystyle =}$

Общее определение

В самых общих чертах вязкие напряжения в жидкости определяются как напряжения, возникающие в результате относительной скорости различных частиц жидкости. Таким образом, вязкие напряжения должны зависеть от пространственных градиентов скорости потока. Если градиенты скорости малы, то в первом приближении вязкие напряжения зависят только от первых производных скорости. ^[13] (Для ньютоновских жидкостей это также линейная зависимость.) В декартовых координатах общее соотношение можно записать как

${\displaystyle \tau _{ij}=\sum _{k}\sum _{\ell }\mu _{ijk\ell }{\frac {\partial v_{k}}{\partial r_{\ell }}},}$

где — тензор вязкости, который отображает тензор градиента скорости на тензор вязкого напряжения . ^[14] Поскольку индексы в этом выражении могут изменяться от 1 до 3, всего имеется 81 «коэффициент вязкости». Однако предположение, что тензор вязкости ранга 2 изотропен, сводит эти 81 коэффициент к трем независимым параметрам , , : ${\displaystyle \mu _{ijk\ell }}$ ${\displaystyle \partial v_{k}/\partial r_{\ell }}$ ${\displaystyle \tau _{ij}}$ ${\displaystyle \mu _{ijkl}}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$

${\displaystyle \mu _{ijk\ell }=\alpha \delta _{ij}\delta _{k\ell }+\beta \delta _{ik}\delta _{j\ell }+\gamma \delta _{i\ell }\delta _{jk},}$

и более того, предполагается, что никакие вязкие силы не могут возникнуть, когда жидкость подвергается простому вращению твердого тела, таким образом , оставляя только два независимых параметра. ^[13] Наиболее обычное разложение происходит в терминах стандартной (скалярной) вязкости и объемной вязкости, таких что и . В векторной записи это выглядит как: ${\displaystyle \beta =\gamma }$ ${\displaystyle \mu }$ ${\displaystyle \kappa }$ ${\displaystyle \alpha =\kappa -{\tfrac {2}{3}}\mu }$ ${\displaystyle \beta =\gamma =\mu }$

${\displaystyle {\boldsymbol {\tau }}=\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v} )^{\mathrm {T} }\right]-\left({\frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } ,}$

где — единичный тензор. ^{[12] [15]} Это уравнение можно рассматривать как обобщенную форму закона вязкости Ньютона. ${\displaystyle \mathbf {\delta } }$

Объемная вязкость (также называемая объемной вязкостью) выражает тип внутреннего трения, которое сопротивляется сжатию или расширению жидкости без сдвига. Знание часто не является необходимым в задачах динамики жидкости. Например, несжимаемая жидкость удовлетворяет и поэтому термин, содержащий выпадает. Более того, часто предполагается пренебрежимо малым для газов, поскольку он находится в одноатомном идеальном газе . ^[12] Одной из ситуаций, в которой может быть важным, является расчет потери энергии в звуковых и ударных волнах , описываемых законом затухания звука Стокса , поскольку эти явления включают быстрые расширения и сжатия. ${\displaystyle \kappa }$ ${\displaystyle \nabla \cdot \mathbf {v} =0}$ ${\displaystyle \kappa }$ ${\displaystyle \kappa }$ ${\displaystyle 0}$ ${\displaystyle \kappa }$

Определяющие уравнения для вязкости не являются фундаментальными законами природы, поэтому их полезность, а также методы измерения или расчета вязкости должны быть установлены с использованием отдельных средств. Потенциальная проблема заключается в том, что вязкость зависит, в принципе, от полного микроскопического состояния жидкости, которое охватывает положения и импульсы каждой частицы в системе. ^[16] Такая очень подробная информация обычно недоступна в реалистичных системах. Однако при определенных условиях можно показать, что большая часть этой информации пренебрежимо мала. В частности, для ньютоновских жидкостей вблизи равновесия и вдали от границ (объемное состояние) вязкость зависит только от зависящих от пространства и времени макроскопических полей (таких как температура и плотность), определяющих локальное равновесие. ^{[16] [17]}

Тем не менее, вязкость все еще может нести немалую зависимость от нескольких свойств системы, таких как температура, давление, а также амплитуда и частота любого внешнего воздействия. Поэтому точные измерения вязкости определяются только относительно конкретного состояния жидкости. ^[18] Для стандартизации сравнений между экспериментами и теоретическими моделями данные о вязкости иногда экстраполируются на идеальные предельные случаи, такие как предел нулевого сдвига или (для газов) предел нулевой плотности .

Транспорт импульса

Теория переноса дает альтернативную интерпретацию вязкости с точки зрения переноса импульса: вязкость — это свойство материала, которое характеризует перенос импульса в жидкости, так же как теплопроводность характеризует перенос тепла , а диффузия (массы) характеризует перенос массы. ^[19] Эта точка зрения подразумевается в законе вязкости Ньютона, , поскольку напряжение сдвига имеет единицы, эквивалентные потоку импульса , т. е. импульсу в единицу времени на единицу площади. Таким образом, можно интерпретировать как указание потока импульса в направлении от одного слоя жидкости к другому. Согласно закону вязкости Ньютона, этот поток импульса происходит через градиент скорости, а величина соответствующего потока импульса определяется вязкостью. ${\displaystyle \tau =\mu (\partial u/\partial y)}$ ${\displaystyle \tau }$ ${\displaystyle \tau }$ ${\displaystyle y}$

Аналогию с переносом тепла и массы можно сделать явной. Так же, как тепло течет от высокой температуры к низкой температуре, а масса течет от высокой плотности к низкой плотности, импульс течет от высокой скорости к низкой скорости. Все эти поведения описываются компактными выражениями, называемыми определяющими соотношениями , одномерные формы которых приведены здесь:

${\displaystyle {\begin{aligned}\mathbf {J} &=-D{\frac {\partial \rho }{\partial x}}&&{\text{(Fick's law of diffusion)}}\\[5pt]\mathbf {q} &=-k_{t}{\frac {\partial T}{\partial x}}&&{\text{(Fourier's law of heat conduction)}}\\[5pt]\tau &=\mu {\frac {\partial u}{\partial y}}&&{\text{(Newton's law of viscosity)}}\end{aligned}}}$

где — плотность, — потоки массы и тепла, — коэффициент диффузии массы и теплопроводность. ^[20] Тот факт, что перенос массы, импульса и энергии (тепла) относится к числу наиболее важных процессов в механике сплошных сред, не является совпадением: это одни из немногих физических величин, которые сохраняются на микроскопическом уровне при столкновениях между частицами. Таким образом, вместо того, чтобы диктоваться быстрыми и сложными микроскопическими временными масштабами взаимодействия, их динамика происходит в макроскопических временных масштабах, как описывается различными уравнениями теории переноса и гидродинамики. ${\displaystyle \rho }$ ${\displaystyle \mathbf {J} }$ ${\displaystyle \mathbf {q} }$ ${\displaystyle D}$ ${\displaystyle k_{t}}$

Ньютоновские и неньютоновские жидкости

Вязкость (наклон каждой линии) различается в зависимости от материала.

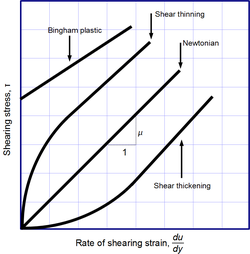
Закон вязкости Ньютона не является фундаментальным законом природы, а скорее конститутивным уравнением (подобно закону Гука , закону Фика и закону Ома ), которое служит для определения вязкости . Его форма мотивирована экспериментами, которые показывают, что для широкого спектра жидкостей не зависит от скорости деформации. Такие жидкости называются ньютоновскими . Газы , вода и многие обычные жидкости могут считаться ньютоновскими в обычных условиях и контекстах. Однако существует много неньютоновских жидкостей , которые значительно отклоняются от этого поведения. Например: ${\displaystyle \mu }$ ${\displaystyle \mu }$

• Загустевающие при сдвиге (дилатантные) жидкости, вязкость которых увеличивается со скоростью деформации сдвига.
• Жидкости, разжижающиеся при сдвиге , вязкость которых уменьшается со скоростью деформации сдвига.
• Тиксотропные жидкости, которые со временем становятся менее вязкими при встряхивании, перемешивании или ином воздействии.
• Реопектические жидкости, которые со временем становятся более вязкими при встряхивании, перемешивании или ином стрессе.
• Пластики Бингама , которые ведут себя как твердое тело при низких напряжениях, но текут как вязкая жидкость при высоких напряжениях.

Коэффициент Траутона — это отношение вязкости растяжения к вязкости сдвига . Для ньютоновской жидкости коэффициент Траутона равен 3. ^{[21] [22]} Жидкости, разжижающиеся при сдвиге, очень часто, но ошибочно, описываются как тиксотропные. ^[23]

Вязкость может также зависеть от физического состояния жидкости (температуры и давления) и других внешних факторов. Для газов и других сжимаемых жидкостей она зависит от температуры и очень медленно меняется с давлением. Вязкость некоторых жидкостей может зависеть от других факторов. Например, магнитореологическая жидкость становится гуще под воздействием магнитного поля , возможно, до такой степени, что ведет себя как твердое тело.

В твердых телах

Вязкие силы, возникающие при течении жидкости, отличаются от упругих сил, которые возникают в твердом теле в ответ на напряжения сдвига, сжатия или растяжения. В то время как в последнем случае напряжение пропорционально величине деформации сдвига, в жидкости оно пропорционально скорости деформации с течением времени. По этой причине Джеймс Клерк Максвелл использовал термин «летучая упругость» для вязкости жидкости.

Однако многие жидкости (включая воду) будут кратковременно реагировать как упругие твердые тела, когда подвергаются внезапному напряжению. И наоборот, многие «твердые тела» (даже гранит ) будут течь как жидкости, хотя и очень медленно, даже при произвольно малом напряжении. ^[24] Такие материалы лучше всего описать как вязкоупругие — то есть обладающие как эластичностью (реакцией на деформацию), так и вязкостью (реакцией на скорость деформации).

Вязкоупругие твердые тела могут проявлять как сдвиговую вязкость, так и объемную вязкость. Растягивающая вязкость представляет собой линейную комбинацию сдвиговой и объемной вязкости, которая описывает реакцию твердого эластичного материала на удлинение. Она широко используется для характеристики полимеров.

В геологии земные материалы, которые демонстрируют вязкую деформацию, по крайней мере на три порядка большую, чем их упругая деформация, иногда называются реидами . ^[25]

Измерение

Вязкость измеряется различными типами вискозиметров и реометров . Тщательный контроль температуры жидкости необходим для получения точных измерений, особенно в таких материалах, как смазочные материалы, вязкость которых может удваиваться при изменении всего на 5 °C. Реометр используется для жидкостей, которые не могут быть определены одним значением вязкости и, следовательно, требуют установки и измерения большего количества параметров, чем в случае с вискозиметром. ^[26]

Для некоторых жидкостей вязкость постоянна в широком диапазоне скоростей сдвига ( ньютоновские жидкости ). Жидкости без постоянной вязкости ( неньютоновские жидкости ) не могут быть описаны одним числом. Неньютоновские жидкости демонстрируют множество различных корреляций между напряжением сдвига и скоростью сдвига.

Одним из наиболее распространенных приборов для измерения кинематической вязкости является стеклянный капиллярный вискозиметр.

В лакокрасочной промышленности вязкость может быть измерена с помощью чашки, в которой измеряется время истечения . Существует несколько видов чашек, например, чашка Зана и чашка Форда для измерения вязкости , причем использование каждого типа в основном варьируется в зависимости от отрасли.

Также используемый в покрытиях, вискозиметр Stormer использует вращение на основе нагрузки для определения вязкости. Вязкость сообщается в единицах Кребса (KU), которые являются уникальными для вискозиметров Stormer.

Вибрационные вискозиметры также могут использоваться для измерения вязкости. Резонансные или вибрационные вискозиметры работают, создавая сдвиговые волны внутри жидкости. В этом методе датчик погружается в жидкость и резонирует на определенной частоте. Когда поверхность датчика сдвигает жидкость, энергия теряется из-за ее вязкости. Эта рассеянная энергия затем измеряется и преобразуется в показания вязкости. Более высокая вязкость вызывает большую потерю энергии. ^{[ необходима цитата ]}

Вязкость растяжения можно измерить с помощью различных реометров , которые применяют растягивающее напряжение .

Объемную вязкость можно измерить с помощью акустического реометра .

Кажущаяся вязкость — это расчет, полученный на основе испытаний, проведенных на буровом растворе, используемом при разработке нефтяных или газовых скважин. Эти расчеты и испытания помогают инженерам разрабатывать и поддерживать свойства бурового раствора в соответствии с требуемыми спецификациями.

Нановязкость (вязкость, определяемая нанозондами) можно измерить с помощью флуоресцентной корреляционной спектроскопии . ^[27]

Единицы

Единицей СИ для измерения динамической вязкости является ньютон -секунда на квадратный метр (Н·с/м ² ), также часто выражаемая в эквивалентных формах паскаль - секунда (Па·с), килограмм на метр в секунду (кг·м ⁻¹ ·с ⁻¹ ) и пуазей (Пл). Единицей СГС является пуаз (П или г·см ⁻¹ ·с ⁻¹ = 0,1 Па·с), ^[28] названный в честь Жана Леонара Мари Пуазейля . Обычно она выражается, особенно в стандартах ASTM , как сантипуаз (сП). Сантипуаз удобен, поскольку вязкость воды при 20 °C составляет около 1 сП, а один сантипуаз равен миллипаскалю-секунде СИ (мПа·с).

Единицей кинематической вязкости в системе СИ является квадратный метр в секунду (м2 ^/ с), тогда как единицей СГС для кинематической вязкости является стокс ( Ст или см2 ^· с ⁻¹ = 0,0001 м2 ^· с ⁻¹ ), названный в честь сэра Джорджа Габриэля Стокса . ^[29] В США стокс иногда используется как форма единственного числа. Вместо этого часто используется дольный сантистокс (сСт), 1 сСт = 1 ^мм2 · с ⁻¹  = 10−6 ^м2  · ^с − ¹ . 1 сСт равен 1 сП, делённому на 1000 кг/м^3, что близко к плотности воды. Кинематическая вязкость воды при 20 °C составляет около 1 сСт.

Наиболее часто используемыми системами единиц США, или имперскими , являются британская гравитационная (BG) и английская инженерная (EE). В системе BG динамическая вязкость измеряется в фунтах -секундах на квадратный фут (фунт-с/фут ² ), а в системе EE — в фунтах-силах -секундах на квадратный фут (фунт-сила-секунда/фут ² ). Фунт и фунт-сила эквивалентны; эти две системы отличаются только тем, как определяются сила и масса. В системе BG фунт является базовой единицей, из которой единица массы (слаг ) определяется Вторым законом Ньютона , тогда как в системе EE единицы силы и массы (фунт-сила и фунт-масса соответственно) определяются независимо через Второй закон с использованием константы пропорциональности g _c .

Кинематическая вязкость измеряется в квадратных футах в секунду (фут2 ^/ с) как в системах BG, так и в системах EE.

Нестандартные единицы включают рейн (фунт-сила·с/дюйм ² ), британскую единицу динамической вязкости. ^[30] В автомобильной промышленности индекс вязкости используется для описания изменения вязкости в зависимости от температуры.

Обратная величина вязкости — текучесть , обычно обозначаемая как или , в зависимости от используемого соглашения, измеряемая в обратном пуазе (P ⁻¹ или см · с · г ⁻¹ ), иногда называемом rhe . Текучесть редко используется в инженерной практике. ^{[ необходима цитата ]} ${\displaystyle \phi =1/\mu }$ ${\displaystyle F=1/\mu }$

В свое время нефтяная промышленность полагалась на измерение кинематической вязкости с помощью вискозиметра Сейболта и выражение кинематической вязкости в единицах универсальных секунд Сейболта (SUS). ^[31] Иногда используются и другие сокращения, такие как SSU ( универсальные секунды Сейболта ) или SUV ( универсальная вязкость Сейболта ). Кинематическая вязкость в сантистоксах может быть преобразована из SUS в соответствии с арифметикой и справочной таблицей, приведенной в ASTM D 2161.

Молекулярное происхождение

Перенос импульса в газах осуществляется посредством дискретных молекулярных столкновений, а в жидкостях — посредством сил притяжения, которые связывают молекулы близко друг к другу. ^[19] Из-за этого динамическая вязкость жидкостей обычно намного больше, чем у газов. Кроме того, вязкость имеет тенденцию увеличиваться с температурой в газах и уменьшаться с температурой в жидкостях.

Выше критической точки жидкость-газ жидкая и газовая фазы заменяются одной сверхкритической фазой . В этом режиме механизмы переноса импульса интерполируются между поведением, подобным жидкости и газу. Например, вдоль сверхкритической изобары (поверхность постоянного давления) кинематическая вязкость уменьшается при низкой температуре и увеличивается при высокой температуре, с минимумом между ними. ^{[32] [33]} Грубая оценка значения при минимуме составляет

${\displaystyle \nu _{\text{min}}={\frac {1}{4\pi }}{\frac {\hbar }{\sqrt {m_{\text{e}}m}}}}$

где — постоянная Планка , — масса электрона , — молекулярная масса. ^[33] ${\displaystyle \hbar }$ ${\displaystyle m_{\text{e}}}$ ${\displaystyle m}$

Однако в целом вязкость системы зависит в деталях от того, как взаимодействуют молекулы, составляющие систему, и для нее не существует простых, но правильных формул. Простейшими точными выражениями являются соотношения Грина–Кубо для линейной сдвиговой вязкости или выражения для функции корреляции переходного времени, выведенные Эвансом и Моррисом в 1988 году. ^[34] Хотя каждое из этих выражений является точным, расчет вязкости плотной жидкости с использованием этих соотношений в настоящее время требует использования компьютерного моделирования молекулярной динамики . Несколько большего прогресса можно добиться для разбавленного газа, поскольку элементарные предположения о том, как молекулы газа движутся и взаимодействуют, приводят к базовому пониманию молекулярного происхождения вязкости. Более сложные методы могут быть построены путем систематического грубого усреднения уравнений движения молекул газа. Примером такого метода является теория Чепмена–Энскога , которая выводит выражения для вязкости разбавленного газа из уравнения Больцмана . ^[17]

Чистые газы

Вязкость в газах возникает в основном из-за молекулярной диффузии , которая переносит импульс между слоями потока. Элементарный расчет для разбавленного газа при температуре и плотности дает ${\displaystyle T}$ ${\displaystyle \rho }$

${\displaystyle \mu =\alpha \rho \lambda {\sqrt {\frac {2k_{\text{B}}T}{\pi m}}},}$

где — постоянная Больцмана , молекулярная масса и числовая константа порядка . Величина , длина свободного пробега , измеряет среднее расстояние, которое молекула проходит между столкновениями. Даже без априорного знания , это выражение имеет нетривиальные последствия. В частности, поскольку обычно обратно пропорциональна плотности и увеличивается с температурой, сама должна увеличиваться с температурой и не зависеть от плотности при фиксированной температуре. Фактически, оба эти предсказания сохраняются в более сложных обработках и точно описывают экспериментальные наблюдения. Напротив, вязкость жидкости обычно уменьшается с температурой. ^{[19] [35]} ${\displaystyle k_{\text{B}}}$ ${\displaystyle m}$ ${\displaystyle \alpha }$ ${\displaystyle 1}$ ${\displaystyle \lambda }$ ${\displaystyle \alpha }$ ${\displaystyle \lambda }$ ${\displaystyle \mu }$

Для жестких упругих сфер диаметром можно вычислить, что дает ${\displaystyle \sigma }$ ${\displaystyle \lambda }$

${\displaystyle \mu ={\frac {\alpha }{\pi ^{3/2}}}{\frac {\sqrt {k_{\text{B}}mT}}{\sigma ^{2}}}.}$

В этом случае не зависит от температуры, поэтому . Однако для более сложных молекулярных моделей зависит от температуры нетривиальным образом, и простые кинетические аргументы, используемые здесь, недостаточны. Что еще более важно, понятие средней длины свободного пробега становится неточным для частиц, которые взаимодействуют в конечном диапазоне, что ограничивает полезность концепции для описания реальных газов. ^[36] ${\displaystyle \lambda }$ ${\displaystyle \mu \propto T^{1/2}}$ ${\displaystyle \lambda }$

Теория Чепмена–Энскога

Метод, разработанный Сиднеем Чепменом и Дэвидом Энскогом в начале 1900-х годов, позволяет более точно рассчитать . ^[17] Он основан на уравнении Больцмана , которое обеспечивает статистическое описание разбавленного газа в терминах межмолекулярных взаимодействий. ^[37] Метод позволяет точно рассчитать для молекулярных моделей, которые более реалистичны, чем жесткие упругие сферы, такие как те, которые включают межмолекулярные притяжения. Это необходимо для воспроизведения правильной температурной зависимости , которая, как показывают эксперименты, увеличивается быстрее, чем тенденция, предсказанная для жестких упругих сфер. ^[19] Действительно, анализ Чепмена–Энскога показывает, что предсказанную температурную зависимость можно настроить, варьируя параметры в различных молекулярных моделях. Простым примером является модель Сазерленда, ^[a] , которая описывает жесткие упругие сферы со слабым взаимным притяжением. В таком случае сила притяжения может рассматриваться пертурбативно , что приводит к простому выражению для : ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle T^{1/2}}$ ${\displaystyle \mu }$

${\displaystyle \mu ={\frac {5}{16\sigma ^{2}}}\left({\frac {k_{\text{B}}mT}{\pi }}\right)^{\!\!1/2}\ \left(1+{\frac {S}{T}}\right)^{\!\!-1},}$

где не зависит от температуры, а определяется только параметрами межмолекулярного притяжения. Для связи с экспериментом удобно переписать как ${\displaystyle S}$

${\displaystyle \mu =\mu _{0}\left({\frac {T}{T_{0}}}\right)^{\!\!3/2}\ {\frac {T_{0}+S}{T+S}},}$

где — вязкость при температуре . Это выражение обычно называют формулой Сазерленда. ^[38] Если известно из экспериментов при и по крайней мере еще одной температуре, то можно рассчитать. Выражения для , полученные таким образом, качественно точны для ряда простых газов. Немного более сложные модели, такие как потенциал Леннарда-Джонса или более гибкий потенциал Ми , могут обеспечить лучшее согласие с экспериментами, но только ценой более непрозрачной зависимости от температуры. Еще одним преимуществом этих более сложных потенциалов взаимодействия является то, что их можно использовать для разработки точных моделей для широкого спектра свойств с использованием тех же параметров потенциала. В ситуациях, когда доступно мало экспериментальных данных, это позволяет получить параметры модели из подгонки к таким свойствам, как равновесия чистой жидкости и пара , прежде чем использовать полученные таким образом параметры для прогнозирования интересующих вязкостей с разумной точностью. ${\displaystyle \mu _{0}}$ ${\displaystyle T_{0}}$ ${\displaystyle \mu }$ ${\displaystyle T=T_{0}}$ ${\displaystyle S}$ ${\displaystyle \mu }$

В некоторых системах предположение о сферической симметрии должно быть оставлено, как в случае паров с высокополярными молекулами , такими как H ₂ O. В этих случаях анализ Чепмена–Энскога значительно сложнее. ^{[39] [40]}

Объемная вязкость

В кинетико-молекулярной картине ненулевая объемная вязкость возникает в газах всякий раз, когда существуют не пренебрежимо малые релаксационные временные масштабы, управляющие обменом энергией между поступательной энергией молекул и их внутренней энергией, например вращательной и колебательной . Таким образом, объемная вязкость существует для одноатомного идеального газа, в котором внутренняя энергия молекул пренебрежимо мала, но не равна нулю для газа, подобного диоксиду углерода , молекулы которого обладают как вращательной, так и колебательной энергией. ^{[41] [42]} ${\displaystyle 0}$

Чистые жидкости

Видео, демонстрирующее три жидкости с разной вязкостью

Эксперимент, демонстрирующий поведение вязкой жидкости с синим красителем для наглядности

В отличие от газов, не существует простой, но точной картины молекулярного происхождения вязкости в жидкостях.

На самом простом уровне описания относительное движение соседних слоев в жидкости в первую очередь противостоит притягивающим молекулярным силам, действующим через границу слоя. В этой картине (правильно) ожидается, что вязкость будет уменьшаться с ростом температуры. Это происходит потому, что рост температуры увеличивает случайное тепловое движение молекул, что облегчает им преодоление их притягивающих взаимодействий. ^[43]

Основываясь на этой визуализации, можно построить простую теорию по аналогии с дискретной структурой твердого тела: группы молекул в жидкости визуализируются как образующие «клетки», которые окружают и заключают в себе отдельные молекулы. ^[44] Эти клетки могут быть заняты или незаняты, и более сильное молекулярное притяжение соответствует более сильным клеткам. Из-за случайного теплового движения молекула «прыгает» между клетками со скоростью, которая изменяется обратно пропорционально силе молекулярного притяжения. В равновесии эти «прыжки» не смещены ни в каком направлении. С другой стороны, для того, чтобы два соседних слоя двигались относительно друг друга, «прыжки» должны быть смещены в направлении относительного движения. Сила, необходимая для поддержания этого направленного движения, может быть оценена для заданной скорости сдвига, что приводит к

где — постоянная Авогадро , — постоянная Планка , — объем моля жидкости , — нормальная температура кипения . Этот результат имеет ту же форму, что и известное эмпирическое соотношение ${\displaystyle N_{\text{A}}}$ ${\displaystyle h}$ ${\displaystyle V}$ ${\displaystyle T_{\text{b}}}$

где и — константы, подобранные из данных. ^{[44] [45]} С другой стороны, несколько авторов выражают осторожность в отношении этой модели. При использовании уравнения ( 1 ) можно столкнуться с ошибками до 30% по сравнению с подгонкой уравнения ( 2 ) к экспериментальным данным. ^[44] Что еще более важно, физические предположения, лежащие в основе уравнения ( 1 ), подверглись критике. ^[46] Также утверждалось, что экспоненциальная зависимость в уравнении ( 1 ) не обязательно описывает экспериментальные наблюдения точнее, чем более простые, неэкспоненциальные выражения. ^{[47] [48]} ${\displaystyle A}$ ${\displaystyle B}$

В свете этих недостатков разработка менее ad hoc модели является вопросом практического интереса. Отказываясь от простоты в пользу точности, можно записать строгие выражения для вязкости, исходя из фундаментальных уравнений движения молекул. Классическим примером такого подхода является теория Ирвинга–Кирквуда. ^[49] С другой стороны, такие выражения даются как средние значения по многочастичным корреляционным функциям и поэтому их трудно применять на практике.

В целом, эмпирически полученные выражения (основанные на существующих измерениях вязкости) представляются единственными последовательно надежными средствами расчета вязкости жидкостей. ^[50]

Локальные изменения атомной структуры, наблюдаемые в переохлажденных жидкостях при охлаждении ниже равновесной температуры плавления либо в терминах радиальной функции распределения g ( r ) ^[51] , либо структурного фактора S ( Q ) ^[52] , как обнаружено, напрямую ответственны за хрупкость жидкости: отклонение температурной зависимости вязкости переохлажденной жидкости от уравнения Аррениуса (2) через модификацию энергии активации для вязкого течения. В то же время равновесные жидкости следуют уравнению Аррениуса.

Смеси и смеси

Газообразные смеси

Та же молекулярно-кинетическая картина однокомпонентного газа может быть применена и к газовой смеси. Например, в подходе Чепмена-Энскога вязкость бинарной смеси газов может быть записана в терминах вязкостей отдельных компонентов , их соответствующих объемных долей и межмолекулярных взаимодействий. ^[17] ${\displaystyle \mu _{\text{mix}}}$ ${\displaystyle \mu _{1,2}}$

Что касается однокомпонентного газа, зависимость от параметров межмолекулярных взаимодействий входит через различные интегралы столкновений, которые могут быть не выражены в замкнутой форме . Чтобы получить пригодные для использования выражения , которые разумно соответствуют экспериментальным данным, интегралы столкновений могут быть вычислены численно или из корреляций. ^[53] В некоторых случаях интегралы столкновений рассматриваются как подгоночные параметры и подгоняются непосредственно к экспериментальным данным. ^[54] Это распространенный подход при разработке справочных уравнений для вязкостей газовой фазы. Примером такой процедуры является подход Сазерленда для однокомпонентного газа, обсуждавшийся выше. ${\displaystyle \mu _{\text{mix}}}$ ${\displaystyle \mu _{\text{mix}}}$

Для газовых смесей, состоящих из простых молекул, было показано, что пересмотренная теория Энскога точно представляет как зависимость вязкости от плотности, так и температуры в широком диапазоне условий. ^{[55] [53]}

Смеси жидкостей

Что касается чистых жидкостей, вязкость смеси жидкостей трудно предсказать из молекулярных принципов. Один из методов заключается в расширении молекулярной теории «клетки», представленной выше, для чистой жидкости. Это можно сделать с разной степенью сложности. Одним из выражений, полученных в результате такого анализа, является уравнение Ледерера–Региерса для бинарной смеси:

${\displaystyle \ln \mu _{\text{blend}}={\frac {x_{1}}{x_{1}+\alpha x_{2}}}\ln \mu _{1}+{\frac {\alpha x_{2}}{x_{1}+\alpha x_{2}}}\ln \mu _{2},}$

где — эмпирический параметр, а и — соответствующие мольные доли и вязкости компонентных жидкостей. ^[56] ${\displaystyle \alpha }$ ${\displaystyle x_{1,2}}$ ${\displaystyle \mu _{1,2}}$

Поскольку смешивание является важным процессом в смазочной и масляной промышленности, существует множество эмпирических и фирменных уравнений для прогнозирования вязкости смеси. ^[56]

Растворы и суспензии

Водные растворы

В зависимости от растворенного вещества и диапазона концентрации водный раствор электролита может иметь большую или меньшую вязкость по сравнению с чистой водой при той же температуре и давлении. Например, 20% раствор хлорида натрия имеет вязкость более чем в 1,5 раза больше, чем у чистой воды, тогда как 20% раствор йодида калия имеет вязкость примерно в 0,91 раза больше, чем у чистой воды.

Идеализированная модель разбавленных электролитических растворов приводит к следующему прогнозу вязкости раствора: ^[57] ${\displaystyle \mu _{s}}$

${\displaystyle {\frac {\mu _{s}}{\mu _{0}}}=1+A{\sqrt {c}},}$

где — вязкость растворителя, — концентрация, — положительная константа, которая зависит как от свойств растворителя, так и от свойств растворенного вещества. Однако это выражение справедливо только для очень разбавленных растворов, имеющих менее 0,1 моль/л. ^[58] Для более высоких концентраций необходимы дополнительные члены, которые учитывают молекулярные корреляции более высокого порядка: ${\displaystyle \mu _{0}}$ ${\displaystyle c}$ ${\displaystyle A}$ ${\displaystyle c}$

${\displaystyle {\frac {\mu _{s}}{\mu _{0}}}=1+A{\sqrt {c}}+Bc+Cc^{2},}$

где и подобраны из данных. В частности, отрицательное значение может объяснить уменьшение вязкости, наблюдаемое в некоторых растворах. Оценочные значения этих констант показаны ниже для хлорида натрия и иодида калия при температуре 25 °C (моль = моль , л = литр ). ^[57] ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle B}$

Подвески

В суспензии твердых частиц (например, сфер микронного размера, взвешенных в масле) эффективная вязкость может быть определена в терминах компонентов напряжения и деформации, которые усредняются по объему, большому по сравнению с расстоянием между взвешенными частицами, но малому по отношению к макроскопическим размерам. ^[59] Такие суспензии обычно демонстрируют неньютоновское поведение. Однако для разбавленных систем в стационарных потоках поведение является ньютоновским, и выражения для могут быть выведены непосредственно из динамики частиц. В очень разбавленной системе с объемной долей , взаимодействия между взвешенными частицами можно игнорировать. В таком случае можно явно рассчитать поле потока вокруг каждой частицы независимо и объединить результаты, чтобы получить . Для сфер это приводит к формуле эффективной вязкости Эйнштейна: ${\displaystyle \mu _{\text{eff}}}$ ${\displaystyle \mu _{\text{eff}}}$ ${\displaystyle \phi \lesssim 0.02}$ ${\displaystyle \mu _{\text{eff}}}$

${\displaystyle \mu _{\text{eff}}=\mu _{0}\left(1+{\frac {5}{2}}\phi \right),}$

где - вязкость суспендирующей жидкости. Линейная зависимость от является следствием пренебрежения межчастичным взаимодействием. Для разбавленных систем в целом можно ожидать, что принимается вид ${\displaystyle \mu _{0}}$ ${\displaystyle \phi }$ ${\displaystyle \mu _{\text{eff}}}$

${\displaystyle \mu _{\text{eff}}=\mu _{0}\left(1+B\phi \right),}$

где коэффициент может зависеть от формы частиц (например, сферы, стержни, диски). ^[60] Экспериментальное определение точного значения затруднено, однако: даже предсказание для сфер не было окончательно подтверждено, при этом различные эксперименты находили значения в диапазоне . Этот недостаток был приписан трудности в контроле экспериментальных условий. ^[61] ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle B=5/2}$ ${\displaystyle 1.5\lesssim B\lesssim 5}$

В более плотных суспензиях приобретает нелинейную зависимость от , что указывает на важность межчастичных взаимодействий. Существуют различные аналитические и полуэмпирические схемы для описания этого режима. На самом базовом уровне к добавляется квадратичный по член : ${\displaystyle \mu _{\text{eff}}}$ ${\displaystyle \phi }$ ${\displaystyle \phi }$ ${\displaystyle \mu _{\text{eff}}}$

${\displaystyle \mu _{\text{eff}}=\mu _{0}\left(1+B\phi +B_{1}\phi ^{2}\right),}$

и коэффициент подгоняется из экспериментальных данных или аппроксимируется из микроскопической теории. Однако некоторые авторы советуют проявлять осторожность при применении таких простых формул, поскольку неньютоновское поведение проявляется в плотных суспензиях ( для сфер), ^[61] или в суспензиях удлиненных или гибких частиц. ^[59] ${\displaystyle B_{1}}$ ${\displaystyle \phi \gtrsim 0.25}$

Существует различие между суспензией твердых частиц, описанной выше, и эмульсией . Последняя представляет собой суспензию крошечных капель, которые сами по себе могут демонстрировать внутреннюю циркуляцию. Наличие внутренней циркуляции может уменьшить наблюдаемую эффективную вязкость, и необходимо использовать различные теоретические или полуэмпирические модели. ^[62]

Аморфные материалы

Общие кривые вязкости стекла ^[63]

В пределе высоких и низких температур вязкое течение в аморфных материалах (например, в стеклах и расплавах) ^{[64] [65] [66]} имеет форму Аррениуса :

${\displaystyle \mu =Ae^{Q/(RT)},}$

где Q — соответствующая энергия активации , заданная в терминах молекулярных параметров; T — температура; R — молярная газовая постоянная ; и A — приблизительно константа. Энергия активации Q принимает разное значение в зависимости от того, рассматривается ли верхний или нижний предел температуры: она изменяется от высокого значения Q _H при низких температурах (в стеклообразном состоянии) до низкого значения Q _L при высоких температурах (в жидком состоянии).

Десятичный логарифм вязкости в зависимости от температуры для B ₂ O ₃ , показывающий два режима

Для промежуточных температур нетривиально меняется с температурой и простая форма Аррениуса не работает. С другой стороны, двухэкспоненциальное уравнение ${\displaystyle Q}$

${\displaystyle \mu =AT\exp \left({\frac {B}{RT}}\right)\left[1+C\exp \left({\frac {D}{RT}}\right)\right],}$

где , , , все константы, обеспечивает хорошее соответствие экспериментальным данным во всем диапазоне температур, в то же время сводясь к правильной форме Аррениуса в пределах низких и высоких температур. Это выражение может быть мотивировано из различных теоретических моделей аморфных материалов на атомном уровне. ^[65] ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle D}$

Двухэкспоненциальное уравнение для вязкости может быть выведено в рамках модели Дайра для переохлажденных жидкостей, где энергетический барьер Аррениуса определяется как высокочастотный модуль сдвига, умноженный на характерный объем сдвига. ^{[67] [68]} После задания температурной зависимости модуля сдвига через тепловое расширение и через отталкивательную часть межмолекулярного потенциала получается еще одно двухэкспоненциальное уравнение: ^[69]

${\displaystyle \mu =\exp {\left\{{\frac {V_{c}C_{G}}{k_{B}T}}\exp {\left[(2+\lambda )\alpha _{T}T_{g}\left(1-{\frac {T}{T_{g}}}\right)\right]}\right\}}}$

где обозначает высокочастотный модуль сдвига материала, оцененный при температуре, равной температуре стеклования , — так называемый объем выталкивания, т. е. это характерный объем группы атомов, вовлеченных в событие выталкивания, посредством которого атом/молекула покидает клетку ближайших соседей, обычно порядка объема, занимаемого несколькими атомами. Кроме того, — коэффициент теплового расширения материала, — параметр, который измеряет крутизну степенного подъема восходящего фланга первого пика функции радиального распределения , и количественно связан с отталкивательной частью межатомного потенциала . ^[69] Наконец, обозначает постоянную Больцмана . ${\displaystyle C_{G}}$ ${\displaystyle T_{g}}$ ${\displaystyle V_{c}}$ ${\displaystyle \alpha _{T}}$ ${\displaystyle \lambda }$ ${\displaystyle k_{B}}$

Вязкость вихрей

При изучении турбулентности в жидкостях общепринятой практической стратегией является игнорирование мелкомасштабных вихрей (или водоворотов ) в движении и расчет крупномасштабного движения с эффективной вязкостью, называемой «вихревой вязкостью», которая характеризует перенос и рассеивание энергии в мелкомасштабном потоке (см. моделирование крупных вихрей ). ^{[70] [71]} В отличие от вязкости самой жидкости, которая должна быть положительной по второму закону термодинамики , вихревая вязкость может быть отрицательной. ^{[72] [73]}

Прогноз

Поскольку вязкость непрерывно зависит от температуры и давления, ее нельзя полностью охарактеризовать конечным числом экспериментальных измерений. Прогностические формулы становятся необходимыми, если экспериментальные значения недоступны при интересующих температурах и давлениях. Эта возможность важна для термофизического моделирования, в котором температура и давление жидкости могут непрерывно изменяться в пространстве и времени. Похожая ситуация возникает для смесей чистых жидкостей, где вязкость непрерывно зависит от соотношений концентраций составляющих жидкостей

Для простейших жидкостей, таких как разбавленные одноатомные газы и их смеси, квантово-механические вычисления ab initio могут точно предсказать вязкость в терминах фундаментальных атомных констант, т.е. без ссылки на существующие измерения вязкости. ^[74] Для особого случая разбавленного гелия неопределенности в вязкости, рассчитанной ab initio, на два порядка меньше неопределенностей в экспериментальных значениях. ^[75]

Для немного более сложных жидкостей и смесей при умеренных плотностях (т. е. докритических плотностях ) пересмотренная теория Энскога может быть использована для прогнозирования вязкости с некоторой точностью. ^{[53] Пересмотренная теория Энскога является предсказательной в том смысле, что прогнозы вязкости могут быть получены с использованием параметров, подобранных к другим} термодинамическим свойствам или свойствам переноса чистой жидкости , таким образом, не требуя априорных экспериментальных измерений вязкости.

Для большинства жидкостей высокоточные вычисления из первых принципов невозможны. Скорее, теоретические или эмпирические выражения должны соответствовать существующим измерениям вязкости. Если такое выражение соответствует высокоточным данным в большом диапазоне температур и давлений, то оно называется «эталонной корреляцией» для этой жидкости. Эталонные корреляции были опубликованы для многих чистых жидкостей; несколько примеров — вода , диоксид углерода , аммиак , бензол и ксенон . ^{[76] [77] [78] [79] [80]} Многие из них охватывают диапазоны температур и давлений, которые охватывают газ, жидкость и сверхкритические фазы.

Программное обеспечение для термофизического моделирования часто опирается на справочные корреляции для прогнозирования вязкости при заданных пользователем температуре и давлении. Эти корреляции могут быть запатентованными . Примерами являются REFPROP ^[81] (запатентованный) и CoolProp ^[82] (с открытым исходным кодом).

Вязкость также можно вычислить с помощью формул, которые выражают ее в терминах статистики отдельных траекторий частиц. Эти формулы включают соотношения Грина-Кубо для линейной сдвиговой вязкости и выражения функции корреляции переходного времени, выведенные Эвансом и Моррисом в 1988 году. ^{[83] [34]} Преимущество этих выражений в том, что они формально точны и действительны для общих систем. Недостатком является то, что они требуют детального знания траекторий частиц, доступного только в вычислительно затратных симуляциях, таких как молекулярная динамика . Также требуется точная модель для межчастичных взаимодействий, которую может быть трудно получить для сложных молекул. ^[84]

Выбранные вещества

В эксперименте с каплей смолы в Университете Квинсленда смола медленно капала через воронку с 1927 года, со скоростью одна капля примерно за десятилетие. Таким образом, вязкость смолы была определена как приблизительно 230 миллиардов (2,3 × 10 ¹¹ ) раз больше, чем у воды. ^[85]

Наблюдаемые значения вязкости варьируются на несколько порядков величины, даже для обычных веществ (см. таблицу порядков величин ниже). Например, 70% раствор сахарозы (сахара) имеет вязкость более чем в 400 раз больше, чем у воды, и в 26 000 раз больше, чем у воздуха. ^[86] Более драматично, что, по оценкам, вязкость смолы в 230 миллиардов раз больше, чем у воды. ^[85]

Вода

Динамическая вязкость воды составляет около 0,89 мПа·с при комнатной температуре (25 °C). Как функцию температуры в градусах Кельвина , вязкость можно оценить с помощью полуэмпирического уравнения Фогеля-Фульчера-Таммана : ${\displaystyle \mu }$

${\displaystyle \mu =A\exp \left({\frac {B}{T-C}}\right)}$

где A = 0,02939 мПа·с, B = 507,88 К и C = 149,3 К. ^[87] Экспериментально определенные значения вязкости также приведены в таблице ниже. Значения при 20 °C являются полезным справочным материалом: там динамическая вязкость составляет около 1 сП, а кинематическая вязкость — около 1 сСт.

Воздух

При стандартных атмосферных условиях (25 °C и давлении 1 бар) динамическая вязкость воздуха составляет 18,5 мкПа·с, что примерно в 50 раз меньше вязкости воды при той же температуре. За исключением очень высокого давления, вязкость воздуха в основном зависит от температуры. Среди множества возможных приближенных формул для температурной зависимости (см. Температурная зависимость вязкости ) одна из них: ^[88]

${\displaystyle \eta _{\text{air}}=2.791\times 10^{-7}\times T^{0.7355}}$

что является точным в диапазоне от −20 °C до 400 °C. Чтобы эта формула была верна, температура должна быть указана в кельвинах ; тогда соответствует вязкости в Па·с. ${\displaystyle \eta _{\text{air}}}$

Мед поливают

Другие распространенные вещества

Оценки порядка величины

В следующей таблице показан диапазон значений вязкости, наблюдаемых в обычных веществах. Если не указано иное, предполагается температура 25 °C и давление 1 атмосфера.

Приведенные значения являются лишь репрезентативными оценками, поскольку они не учитывают неопределенности измерений, изменчивость определений материалов или неньютоновское поведение.

Смотрите также

• Приборная панель
• Число Деборы
• Дилатант
• Жидкость Гершеля-Балкли
• Смеситель высокой вязкости
• Синдром гипервязкости
• Характеристическая вязкость
• Невязкий поток
• Метод Джобака (оценка вязкости жидкости по молекулярной структуре)
• Эффект Кейя
• Микровязкость
• Число Мортона
• Давление масла
• Квазитвердый
• Реология
• Стокса поток
• Сверхтекучий гелий-4
• Вязкопластичность
• Модели вязкости смесей
• чашка Зана

Ссылки

Сноски

1. Дальнейшее обсуждение основано на работе Chapman & Cowling 1970, стр. 232–237.
2. Эти материалы являются в высшей степени неньютоновскими .

Цитаты

1. "Вязкость". Encyclopedia Britannica . 26 июня 2023 г. Получено 4 августа 2023 г.
2. Растем вместе с наукой. Маршалл Кавендиш . 2006. стр. 1928. ISBN 978-0-7614-7521-7.
3. Э. Дейл Мартин (1961). Исследование ламинарного течения сжимаемой вязкой жидкости в трубе, ускоренного осевой силой тела, с приложением к магнитогазодинамике. NASA . стр. 7.
4. Балеску 1975, стр. 428–429.
5. Ландау и Лифшиц 1987.
6. Харпер, Дуглас (nd). "вязкий (прил.)". Онлайн-словарь этимологии . Архивировано из оригинала 1 мая 2019 года . Получено 19 сентября 2019 года .
7. Мьюис и Вагнер 2012, стр. 19.
8. Стритер, Уайли и Бедфорд 1998.
9. Холман 2002.
10. Инкропера и др. 2007.
11. Нич и др. 1997.
12. Bird, Stewart & Lightfoot 2007, стр. 19.
13. Ландау и Лифшиц 1987, стр. 44–45.
14. Bird, Stewart & Lightfoot 2007, стр. 18: В этом источнике используется альтернативная система знаков, которая здесь изменена на противоположную.
15. Ландау и Лифшиц 1987, стр. 45.
16. Balescu 1975.
17. Чепмен и Коулинг 1970.
18. Миллат 1996.
19. Берд, Стюарт и Лайтфут 2007.
20. Шредер 1999.
21. Ружанска и др. 2014, стр. 47–55.
22. Траутон 1906, стр. 426–440.
23. Мьюис и Вагнер, 2012, стр. 228–230.
24. Кумагай, Сасадзима и Ито 1978, стр. 157–161.
25. Шерер, Парденек и Святек 1988, стр. 14.
26. Ханнан 2007.
27. Квапишевска и др. 2020.
28. Макнот и Уилкинсон 1997, баланс.
29. Гилленбок 2018, стр. 213.
30. "Какая единица измерения называется рейн?". sizes.com . Получено 23 декабря 2023 г. .
31. ASTM D2161: Стандартная практика преобразования кинематической вязкости в универсальную вязкость по Сейболту или в вязкость по Сейболту по фуролу , ASTM , 2005, стр. 1
32. Траченко и Бражкин 2020.
33. Траченко и Бражкин 2021.
34. Эванс и Моррис 1988.
35. Беллак, Мортессан и Батруни 2004.
36. Чепмен и Коулинг 1970, стр. 103.
37. Черчиньяни 1975.
38. Сазерленд 1893, стр. 507–531.
39. Берд, Стюарт и Лайтфут 2007, стр. 25–27.
40. Чепмен и Коулинг 1970, стр. 235–237.
41. Чепмен и Коулинг 1970, стр. 197, 214–216.
42. Крамер 2012, стр. 066102-2.
43. Рид и Шервуд 1958, стр. 202.
44. Bird, Stewart & Lightfoot 2007, стр. 29–31.
45. Рид и Шервуд 1958, стр. 203–204.
46. Хильдебранд 1977.
47. Хильдебранд 1977, стр. 37.
48. Эгельстафф 1992, стр. 264.
49. Ирвинг и Кирквуд 1949, стр. 817–829.
50. Рид и Шервуд 1958, стр. 206–209.
51. Louzguine-Luzgin, DV (2022-10-18). "Структурные изменения в металлических стеклообразующих жидкостях при охлаждении и последующем стекловании в связи с их свойствами". Materials . 15 (20): 7285. Bibcode :2022Mate...15.7285L. doi : 10.3390/ma15207285 . ISSN  1996-1944. PMC 9610435 . PMID  36295350. 
52. Kelton, KF (2017-01-18). "Кинетическая и структурная хрупкость — корреляция между структурами и динамикой в ​​металлических жидкостях и стеклах" . Journal of Physics: Condensed Matter . 29 (2): 023002. Bibcode : 2017JPCM...29b3002K. doi : 10.1088/0953-8984/29/2/023002. ISSN  0953-8984. PMID  27841996.
53. Jervell, Vegard G.; Wilhelmsen, Øivind (2023-06-08). "Пересмотренная теория Энскога для жидкостей Ми: прогнозирование коэффициентов диффузии, коэффициентов термодиффузии, вязкостей и теплопроводностей" . Журнал химической физики . 158 (22). Bibcode :2023JChPh.158v4101J. doi :10.1063/5.0149865. ISSN  0021-9606. PMID  37290070. S2CID  259119498.
54. Lemmon, EW; Jacobsen, RT (2004-01-01). "Уравнения вязкости и теплопроводности для азота, кислорода, аргона и воздуха" . International Journal of Thermophysics . 25 (1): 21–69. Bibcode :2004IJT....25...21L. doi :10.1023/B:IJOT.0000022327.04529.f3. ISSN  1572-9567. S2CID  119677367.
55. Лопес де Аро, М.; Коэн, Э. Г. Д.; Кинкейд, Дж. М. (1983-03-01). "Теория Энскога для многокомпонентных смесей. I. Линейная теория переноса" . Журнал химической физики . 78 (5): 2746–2759. Bibcode : 1983JChPh..78.2746L. doi : 10.1063/1.444985. ISSN  0021-9606.
56. Жмудь 2014, стр. 22.
57. Вишванат и др. 2007.
58. Абдулагатов, Зейналова и Азизов 2006, стр. 75–88.
59. Bird, Stewart & Lightfoot 2007, стр. 31–33.
60. Берд, Стюарт и Лайтфут 2007, стр. 32.
61. Mueller, Llewellin & Mader 2009, стр. 1201–1228.
62. Берд, Стюарт и Лайтфут 2007, стр. 33.
63. Флюгель 2007.
64. Доремус 2002, стр. 7619–7629.
65. Ojovan, Travis & Hand 2007, стр. 415-107.
66. Оджован и Ли 2004, стр. 3803–3810.
67. Дайр, Олсен и Кристенсен 1996, стр. 2171.
68. Хекшер и Дайр 2015.
69. Крауссер, Самвер и Закконе, 2015, стр. 13762.
70. Берд, Стюарт и Лайтфут 2007, стр. 163.
71. Lesieur 2012, стр. 2–.
72. Сивашинский и Яхот 1985, с. 1040.
73. Се и Левченко 2019, с. 045434.
74. Шарипов и Бенитес 2020.
75. Роуленд, Аль Гафри и Мэй 2020.
76. Хубер и др. 2009.
77. Лаесеке и Музни 2017.
78. Моногениду, Ассаэль и Хубер 2018.
79. Авгери и др. 2014.
80. Вельяду и др. 2021.
81. "Refprop". NIST . Nist.gov. 18 апреля 2013 г. Архивировано из оригинала 2022-02-09 . Получено 2022-02-15 .
82. Белл и др. 2014.
83. Эванс и Моррис 2007.
84. Магинн и др. 2019.
85. Эджворт, Далтон и Парнелл 1984, стр. 198–200.
86. Битва 2018.
87. Вишванатх и Натараджан 1989, стр. 714–715.
88. tec-science (2020-03-25). "Вязкость жидкостей и газов". tec-science . Архивировано из оригинала 2020-04-19 . Получено 2020-05-07 .
89. 2009.
90. Янниотис, Скальци и Карабурниоти 2006, стр. 372–377.
91. Коочеки и др. 2009, стр. 596–602.
92. Citerne, Carreau & Moan 2001, стр. 86–96.
93. Кестин, Халифа и Уэйкхэм 1977.
94. Ассаэль и др. 2018.
95. Кестин, Ро и Уэйкхем 1972.
96. Розенсон, МакКормик и Урец 1996.
97. Чжао и др. 2021.
98. Сагдеев и др. 2019.
99. Вальцер, Хендель и Баумгарднер.

Источники

• Абдулагатов, Ильмутдин М.; Зейналова, Аделя Б.; Азизов, Назим Д. (2006). "Экспериментальные коэффициенты вязкости B водных растворов LiCl". Журнал молекулярных жидкостей . 126 (1–3): 75–88. doi :10.1016/j.molliq.2005.10.006. ISSN  0167-7322.
• Assael, MJ; et al. (2018). "Эталонные значения и эталонные корреляции для теплопроводности и вязкости жидкостей". Журнал справочных данных по физике и химии . 47 (2): 021501. Bibcode : 2018JPCRD..47b1501A. doi : 10.1063/1.5036625. ISSN 0047-2689  . PMC  6463310. PMID  30996494.
• Avgeri, S.; Assael, MJ; Huber, ML; Perkins, RA (2014). "Справочная корреляция вязкости бензола от тройной точки до 675 К и до 300 МПа". Журнал справочных физических и химических данных . 43 (3). AIP Publishing: 033103. Bibcode : 2014JPCRD..43c3103A. doi : 10.1063/1.4892935. ISSN  0047-2689.
• Балеску, Раду (1975). Равновесная и неравновесная статистическая механика. John Wiley & Sons. ISBN 978-0-471-04600-4. Архивировано из оригинала 2020-03-16 . Получено 2019-09-18 .
• Белл, Ян Х.; Вронски, Йоррит; Куоилин, Сильвен; Леморт, Винсент (27.01.2014). «Оценка термофизических свойств чистой и псевдочистой жидкости и библиотека термофизических свойств с открытым исходным кодом CoolProp». Исследования промышленной и инженерной химии . 53 (6). Американское химическое общество (ACS): 2498–2508. doi :10.1021/ie4033999. ISSN  0888-5885. PMC 3944605.  PMID 24623957  .
• Беллак, Майкл; Мортессань, Фабрис; Батруни, Г. Джордж (2004). Равновесная и неравновесная статистическая термодинамика . Издательство Кембриджского университета. ISBN 978-0-521-82143-8.

• Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (2007). Явления переноса (2-е изд.). John Wiley & Sons, Inc. ISBN 978-0-470-11539-8. Архивировано из оригинала 2020-03-02 . Получено 2019-09-18 .

• Берд, Р. Брайон; Армстронг, Роберт К.; Хассагер, Оле (1987), Динамика полимерных жидкостей, Том 1: Механика жидкости (2-е изд.), John Wiley & Sons

• Черчиньяни, Карло (1975). Теория и применение уравнения Больцмана . Elsevier. ISBN 978-0-444-19450-3.

• Чепмен, Сидней ; Коулинг, TG (1970). Математическая теория неоднородных газов (3-е изд.). Cambridge University Press. ISBN 978-0-521-07577-0.

• Citerne, Guillaume P.; Carreau, Pierre J.; Moan, Michel (2001). «Реологические свойства арахисового масла». Rheologica Acta . 40 (1): 86–96. doi :10.1007/s003970000120. S2CID  94555820.

• Cramer, MS (2012). "Численные оценки объемной вязкости идеальных газов". Physics of Fluids . 24 (6): 066102–066102–23. Bibcode :2012PhFl...24f6102C. doi :10.1063/1.4729611. hdl : 10919/47646 . Архивировано из оригинала 2022-02-15 . Получено 2020-09-19 .

• Doremus, RH (2002). «Вязкость кремнезема». J. Appl. Phys . 92 (12): 7619–7629. Bibcode : 2002JAP....92.7619D. doi : 10.1063/1.1515132.
• Dyre, JC; Olsen, NB; Christensen, T. (1996). "Модель локального упругого расширения для энергий активации вязкого течения стеклообразующих молекулярных жидкостей" (PDF) . Physical Review B . 53 (5): 2171–2174. Bibcode :1996PhRvB..53.2171D. doi : 10.1103/PhysRevB.53.2171 . PMID  9983702.
• Edgeworth, R.; Dalton, BJ; Parnell, T. (1984). "The pitch drop experimental" . European Journal of Physics . 5 (4): 198–200. Bibcode :1984EJPh....5..198E. doi :10.1088/0143-0807/5/4/003. S2CID  250769509. Архивировано из оригинала 28.03.2013 . Получено 31.03.2009 .
• Эгельстафф, Пенсильвания (1992). Введение в жидкое состояние (2-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-851012-3.
• Эванс, Денис Дж .; Моррис, Гэри П. (2007). Статистическая механика неравновесных жидкостей. ANU Press. ISBN 978-1-921313-22-6. JSTOR  j.ctt24h99q. Архивировано из оригинала 2022-01-10 . Получено 2022-01-10 .
• Эванс, Денис Дж.; Моррис, Гэри П. (15 октября 1988 г.). «Функции корреляции во времени и реология жидкостей». Physical Review A. 38 ( 8): 4142–4148. Bibcode : 1988PhRvA..38.4142E. doi : 10.1103/PhysRevA.38.4142. PMID  9900865.
• Fellows, PJ (2009). Технология обработки пищевых продуктов: принципы и практика (3-е изд.). Woodhead. ISBN 978-1-84569-216-2.

• Флюгель, Александр (2007). "Расчет вязкости стекол". Glassproperties.com. Архивировано из оригинала 2010-11-27 . Получено 2010-09-14 .
• Гиббс, Филипп (январь 1997). "Стекло жидкое или твердое?". math.ucr.edu . Архивировано из оригинала 29 марта 2007 . Получено 19 сентября 2019 .
• Gyllenbok, Jan (2018). "Энциклопедия исторической метрологии, весов и мер: Том 1". Энциклопедия исторической метрологии, весов и мер . Том 1. Birkhäuser. ISBN 978-3-319-57598-8.
• Ханнан, Генри (2007). Справочник технического специалиста по рецептурам для промышленных и бытовых чистящих средств . Уокеша, Висконсин: Kyral LLC. стр. 7. ISBN 978-0-615-15601-9.
• Hecksher, Tina; Dyre, Jeppe C. (2015-01-01). "Обзор экспериментов по тестированию модели толкания" . Journal of Non-Crystalline Solids . 7th IDMRCS: Relaxation in Complex Systems. 407 : 14–22. Bibcode :2015JNCS..407...14H. doi :10.1016/j.jnoncrysol.2014.08.056. ISSN  0022-3093. Архивировано из оригинала 2022-02-15 . Получено 2021-10-17 .
• Хильдебранд, Джоэл Генри (1977). Вязкость и диффузность: предиктивное лечение . John Wiley & Sons. ISBN 978-0-471-03072-0.

• Холман, Джек Филип (2002). Теплопередача. McGraw-Hill. ISBN 978-0-07-112230-6. Архивировано из оригинала 2020-03-15 . Получено 2019-09-18 .
• Huber, ML; Perkins, RA; Laesecke, A.; Friend, DG; Sengers, JV; Assael, MJ; Metaxa, IN; Vogel, E.; Mares, R.; Miyagawa, K. (2009). "Новая международная формулировка для вязкости H2O". Journal of Physical and Chemical Reference Data . 38 (2). AIP Publishing: 101–125. Bibcode : 2009JPCRD..38..101H. doi : 10.1063/1.3088050. ISSN  0047-2689.
• Incropera, Frank P.; et al. (2007). Основы тепло- и массообмена. Wiley. ISBN 978-0-471-45728-2. Архивировано из оригинала 2020-03-11 . Получено 2019-09-18 .
• Ирвинг, Дж. Х.; Кирквуд, Джон Г. (1949). «Статистическая механическая теория процессов переноса. IV. Уравнения гидродинамики». J. Chem. Phys . 18 (6): 817–829. doi :10.1063/1.1747782.

• Кестин, Дж.; Ро, СТ; Уэйкхэм, ВА (1972). «Вязкость благородных газов в диапазоне температур 25–700 °C». Журнал химической физики . 56 (8): 4119–4124. Bibcode : 1972JChPh..56.4119K. doi : 10.1063/1.1677824 . ISSN  0021-9606.
• Кестин, Дж.; Халифа, Х. Э.; Уэйкхем, ВА (1977). «Вязкость пяти газообразных углеводородов». Журнал химической физики . 66 (3): 1132. Bibcode : 1977JChPh..66.1132K. doi : 10.1063/1.434048.
• Koocheki, Arash; et al. (2009). «Реологические свойства кетчупа как функция различных гидроколлоидов и температуры». International Journal of Food Science & Technology . 44 (3): 596–602. doi :10.1111/j.1365-2621.2008.01868.x.
• Krausser, J.; Samwer, K.; Zaccone, A. (2015). «Мягкость межатомного отталкивания напрямую контролирует хрупкость переохлажденных металлических расплавов». Труды Национальной академии наук США . 112 (45): 13762–13767. arXiv : 1510.08117 . Bibcode : 2015PNAS..11213762K. doi : 10.1073/pnas.1503741112 . PMC  4653154. PMID  26504208 .
• Kumagai, Naoichi; Sasajima, Sadao; Ito, Hidebumi (15 февраля 1978 г.). «Длительная ползучесть горных пород: результаты с крупными образцами, полученные примерно за 20 лет, и результаты с мелкими образцами, полученные примерно за 3 года». Журнал Общества материаловедения (Япония) . 27 (293): 157–161. NAID  110002299397. Архивировано из оригинала 21.05.2011 . Получено 16.06.2008 .
• Квапишевская, Карина; Щепаньский, Кшиштоф; Кальварчик, Томаш; Михальска, Бернадета; Паталас-Кравчик, Полина; Шиманский, Енджей; Андрышевский, Томаш; Иван, Михалина; Душиньский, Ежи; Холист, Роберт (2020). «Наномасштабная вязкость цитоплазмы сохраняется в клеточных линиях человека». Журнал физической химии . 11 (16): 6914–6920. doi : 10.1021/acs.jpclett.0c01748 . ПМК  7450658 . ПМИД  32787203.
• Laesecke, Arno; Muzny, Chris D. (2017). "Reference Correlation for the Viscosity of Carbon Dioxide". Журнал справочных физических и химических данных . 46 (1). Издательство AIP: 013107. Bibcode : 2017JPCRD..46a3107L . doi : 10.1063/1.4977429. ISSN  0047-2689. PMC  5514612. PMID  28736460.
• Ландау, LD ; Лифшиц, Э.М. (1987). Механика жидкости (2-е изд.). Эльзевир. ISBN 978-0-08-057073-0. Архивировано из оригинала 2020-03-21 . Получено 2019-09-18 .
• Maginn, Edward J.; Messerly, Richard A.; Carlson, Daniel J.; Roe, Daniel R.; Elliott, J. Richard (2019). "Лучшие практики вычисления свойств переноса 1. Самодиффузия и вязкость из равновесной молекулярной динамики [Статья v1.0]". Living Journal of Computational Molecular Science . 1 (1). Университет Колорадо в Боулдере. doi : 10.33011/livecoms.1.1.6324 . ISSN  2575-6524. S2CID  104357320.
• Monogenidou, SA; Assael, MJ; Huber, ML (2018). "Эталонная корреляция для вязкости аммиака от тройной точки до 725 К и до 50 МПа". Журнал справочных физических и химических данных . 47 (2). AIP Publishing: 023102. Bibcode : 2018JPCRD..47b3102M. doi : 10.1063/1.5036724. ISSN  0047-2689. PMC 6512859.  PMID 31092958  .
• Лесье, Марсель (2012). Турбулентность в жидкостях: стохастическое и численное моделирование. Springer. ISBN 978-94-009-0533-7. Архивировано из оригинала 2020-03-14 . Получено 2018-11-30 .
• Мьюис, Ян; Вагнер, Норман Дж. (2012). Реология коллоидной суспензии. Cambridge University Press. ISBN 978-0-521-51599-3. Архивировано из оригинала 2020-03-14 . Получено 2018-12-10 .
• McNaught, AD; Wilkinson, A. (1997). "уравновешенность". IUPAC. Compendium of Chemical Terminology ("Золотая книга") . SJ Chalk (2-е изд.). Oxford: Blackwell Scientific. doi :10.1351/goldbook. ISBN 0-9678550-9-8.
• Миллат, Йорген (1996). Транспортные свойства жидкостей: их корреляция, прогнозирование и оценка . Кембридж: Cambridge University Press. ISBN 978-0-521-02290-3. OCLC  668204060.
• Мюллер, С.; Ллевеллин, Э. В.; Мадер, Х. М. (2009). «Реология суспензий твердых частиц». Труды Королевского общества A: Математические, физические и инженерные науки . 466 (2116): 1201–1228. doi :10.1098/rspa.2009.0445. ISSN  1364-5021.
• Нич, Милослав; и др., ред. (1997). "динамическая вязкость, η ". Сборник химической терминологии ИЮПАК . Оксфорд: Blackwell Scientific Publications. doi :10.1351/goldbook. ISBN 978-0-9678550-9-7.
• Оджован, MI; Ли, WE (2004). «Вязкость сетевых жидкостей в подходе Доремуса». J. Appl. Phys . 95 (7): 3803–3810. Bibcode : 2004JAP....95.3803O. doi : 10.1063/1.1647260.
• Ojovan, MI; Travis, KP; Hand, RJ (2007). "Термодинамические параметры связей в стеклообразных материалах из соотношений вязкости и температуры" (PDF) . J. Phys.: Condens. Matter . 19 (41): 415107. Bibcode :2007JPCM...19O5107O. doi :10.1088/0953-8984/19/41/415107. PMID  28192319. S2CID  24724512. Архивировано (PDF) из оригинала 25.07.2018 . Получено 27.09.2019 .
• Plumb, Robert C. (1989). "Старинные оконные стекла и поток переохлажденных жидкостей". Journal of Chemical Education . 66 (12): 994. Bibcode : 1989JChEd..66..994P. doi : 10.1021/ed066p994. Архивировано из оригинала 26.08.2005 . Получено 25.12.2013 .
• Рапапорт, Д.К. (2004). Искусство моделирования молекулярной динамики (2-е изд.). Cambridge University Press. ISBN 978-0-521-82568-9. Архивировано из оригинала 2018-06-25 . Получено 2022-01-10 .
• Рид, Роберт С.; Шервуд, Томас К. (1958). Свойства газов и жидкостей . McGraw-Hill.
• Рейф, Ф. (1965), Основы статистической и тепловой физики , McGraw-Hill. Продвинутое лечение.
• Розенсон, RS; Маккормик, A; Урец, EF (1996-08-01). «Распределение значений вязкости крови и биохимических коррелятов у здоровых взрослых». Клиническая химия . 42 (8). Oxford University Press (OUP): 1189–1195. doi : 10.1093/clinchem/42.8.1189 . ISSN  0009-9147. PMID  8697575.
• Роуленд, Даррен; Аль Гафри, Саиф ЗС; Мэй, Эрик Ф. (2020-03-01). «Широкомасштабные референтные корреляции для свойств переноса разбавленного газа на основе расчетов Ab Initio и измерений коэффициента вязкости». Журнал справочных физических и химических данных . 49 (1). Издательство AIP: 013101. Bibcode : 2020JPCRD..49a3101X. doi : 10.1063/1.5125100. ISSN  0047-2689. S2CID  213794612.
• Różańska, S.; Różański, J.; Ochowiak, M.; Mitkowski, PT (2014). "Измерения вязкости при растяжении концентрированных эмульсий с использованием устройства с противолежащими соплами" (PDF) . Brazilian Journal of Chemical Engineering . 31 (1): 47–55. doi : 10.1590/S0104-66322014000100006 . ISSN  0104-6632. Архивировано (PDF) из оригинала 2020-05-08 . Получено 2019-09-19 .
• Рамбл, Джон Р., ред. (2018). CRC Handbook of Chemistry and Physics (99-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-138-56163-2.
• Сагдеев, Дамир; Габитов, Ильгиз; Исянов, Чингиз; Хайрутдинов, Венер; Фарахов, Мансур; Зарипов, Зуфар; Абдулагатов, Ильмутдин (2019-04-22). "Плотность и вязкость олеиновой кислоты при атмосферном давлении". Журнал Американского общества нефтехимиков . 96 (6). Wiley: 647–662. doi :10.1002/aocs.12217. ISSN  0003-021X. S2CID  150156106.
• Шерер, Джордж В.; Парденек, Сандра А.; Свёнтек, Роуз М. (1988). «Вязкоупругость в силикагеле». Журнал некристаллических твердых тел . 107 (1): 14. Bibcode : 1988JNCS..107...14S. doi : 10.1016/0022-3093(88)90086-5.
• Шредер, Дэниел В. (1999). Введение в тепловую физику. Эддисон Уэсли. ISBN 978-0-201-38027-9. Архивировано из оригинала 2020-03-10 . Получено 2018-11-30 .
• Шарипов, Феликс; Бенитес, Виктор Дж. (2020-07-01). "Коэффициенты переноса многокомпонентных смесей благородных газов на основе потенциалов ab initio: вязкость и теплопроводность". Physics of Fluids . 32 (7). AIP Publishing: 077104. arXiv : 2006.08687 . Bibcode :2020PhFl...32g7104S. doi :10.1063/5.0016261. ISSN  1070-6631. S2CID  219708359.
• Сивашинский, В.; Яхот, Г. (1985). "Эффект отрицательной вязкости в крупномасштабных потоках". Физика жидкостей . 28 (4): 1040. Bibcode :1985PhFl...28.1040S. doi :10.1063/1.865025.
• Стритер, Виктор Лайл; Уайли, Э. Бенджамин; Бедфорд, Кит В. (1998). Механика жидкостей. WCB/McGraw Hill. ISBN 978-0-07-062537-2. Архивировано из оригинала 2020-03-16 . Получено 2019-09-18 .
• Sutherland, William (1893). "LII. Thevascular of gass and molecular force" (PDF) . The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 36 (223): 507–531. doi :10.1080/14786449308620508. ISSN  1941-5982. Архивировано (PDF) из оригинала 20.07.2019 . Получено 18.09.2019 .
• Саймон, Кит Р. (1971). Механика (3-е изд.). Эддисон-Уэсли. ISBN 978-0-201-07392-8. Архивировано из оригинала 2020-03-11 . Получено 2019-09-18 .
• Траченко, К.; Бражкин, В.В. (2020-04-22). "Минимальная квантовая вязкость из фундаментальных физических констант". Science Advances . 6 (17). Американская ассоциация содействия развитию науки (AAAS): eaba3747. arXiv : 1912.06711 . Bibcode :2020SciA....6.3747T. doi :10.1126/sciadv.aba3747. ISSN  2375-2548. PMC  7182420 . PMID  32426470.
• Траченко, Костя; Бражкин, Вадим В. (2021-12-01). "Квантовая механика вязкости" (PDF) . Physics Today . 74 (12). AIP Publishing: 66–67. Bibcode :2021PhT....74l..66T. doi :10.1063/pt.3.4908. ISSN  0031-9228. S2CID  244831744. Архивировано (PDF) из оригинала 2022-01-10 . Получено 2022-01-10 .
• Trouton, Fred. T. (1906). «О коэффициенте вязкого сцепления и его связи с коэффициентом вязкости». Труды Королевского общества A: Математические, физические и инженерные науки . 77 (519): 426–440. Bibcode :1906RSPSA..77..426T. doi : 10.1098/rspa.1906.0038 . ISSN  1364-5021.
• Веллиаду, Данай; Тасиду, Катерина А.; Антониадис, Константинос Д.; Ассаэль, Марк Дж.; Перкинс, Ричард А.; Хубер, Марсия Л. (2021-03-25). "Эталонная корреляция для вязкости ксенона от тройной точки до 750 К и до 86 МПа". Международный журнал термофизики . 42 (5). Springer Science and Business Media LLC: 74. Bibcode : 2021IJT....42...74V. doi : 10.1007/s10765-021-02818-9. ISSN  0195-928X. PMC 8356199.  PMID 34393314  .
• Вишванат, Д.С.; Натараджан, Г. (1989). Справочник по вязкости жидкостей . Hemisphere Publishing Corporation. ISBN 0-89116-778-1.
• Вишванат, Дабир С. и др. (2007). Вязкость жидкостей: теория, оценка, эксперимент и данные . Springer. ISBN 978-1-4020-5481-5.
• Вальцер, Уве; Хендель, Роланд; Баумгарднер, Джон, «Вязкость мантии и толщина конвективных нисходящих потоков», igw.uni-jena.de , архивировано из оригинала 2007-06-11
• Xie, Hong-Yi; Levchenko, Alex (23 января 2019 г.). "Отрицательная вязкость и вихревой поток несбалансированной электронно-дырочной жидкости в графене". Phys. Rev. B . 99 (4): 045434. arXiv : 1807.04770 . Bibcode :2019PhRvB..99d5434X. doi :10.1103/PhysRevB.99.045434. S2CID  51792702.
• Янниотис, С.; Скалци, С.; Карабурниоти, С. (февраль 2006 г.). «Влияние содержания влаги на вязкость меда при разных температурах». Журнал пищевой инженерии . 72 (4): 372–377. doi :10.1016/j.jfoodeng.2004.12.017.
• Чжао, Мэнцзин; Ван, Юн; Ян, Шуфэн; Ли, Цзиншэ; Лю, Вэй; Сун, Чжаоци (2021). «Поведение потока и теплопередача расплавленной стали в двухручьевом промежуточном ковше, нагреваемом плазмой». Журнал исследований и технологий материалов . 13. Elsevier BV: 561–572. doi : 10.1016/j.jmrt.2021.04.069 . ISSN  2238-7854. S2CID  236277034.
• Жмудь, Борис (2014). "Уравнения смешивания вязкости" (PDF) . Lube-Tech:93. Lube . № 121. стр. 22–27. Архивировано (PDF) из оригинала 2018-12-01 . Получено 2018-11-30 .
• "База данных термодинамических и транспортных свойств NIST Reference Fluid (REFPROP): Версия 10". NIST . 2018-01-01. Архивировано из оригинала 2021-12-16 . Получено 2021-12-23 .
• tec-science (2020-03-25). "Вязкость жидкостей и газов". tec-science . Архивировано из оригинала 2020-04-19 . Получено 2020-05-07 .

Внешние ссылки

• Вязкость - Фейнмановские лекции по физике
• Свойства жидкости – высокоточный расчет вязкости для часто встречающихся чистых жидкостей и газов.
• Таблица характеристик жидкостей – таблица вязкостей и давлений паров для различных жидкостей.
• Gas Dynamics Toolbox – рассчитать коэффициент вязкости для смесей газов
• Измерение вязкости стекла – измерение вязкости, единицы вязкости и фиксированные точки, расчет вязкости стекла
• Кинематическая вязкость – преобразование кинематической вязкости в динамическую.
• Физические характеристики воды – таблица вязкости воды в зависимости от температуры
• Расчет температурно-зависимых динамических вязкостей для некоторых распространенных компонентов
• Искусственная вязкость
• Вязкость воздуха, динамическая и кинематическая, Engineers Edge