Теорема о трех промежутках

О расстояниях между точками на окружности

В математике теорема о трех промежутках , теорема о трех расстояниях или гипотеза Штейнгауза утверждает, что если разместить n точек на окружности под углами θ , 2 θ , 3 θ , ... от начальной точки, то между парами точек в соседних положениях по окружности будет не более трех различных расстояний. Когда есть три расстояния, наибольшее из трех всегда равно сумме двух других. ^[1] Если θ не является рациональным кратным π , также будет не менее двух различных расстояний.

Этот результат был выдвинут Гуго Штейнхаузом и доказан в 1950-х годах Верой Т. Шош , Яношем Шураньи  [hu] и Станиславом Сверчковским ; позже другие добавили больше доказательств. Приложения теоремы о трех зазорах включают изучение роста растений и музыкальных систем настройки, а также теорию отражения света в зеркальном квадрате.

Заявление

Теорему о трех промежутках можно сформулировать геометрически в терминах точек на окружности. В этой форме она утверждает, что если разместить точки на окружности под углами от начальной точки, то между парами точек в соседних позициях по окружности будет не более трех различных расстояний. Эквивалентная и более алгебраическая форма включает дробные части кратных действительного числа . Она утверждает, что для любого положительного действительного числа и целого числа дробные части чисел делят единичный интервал на подынтервалы с не более чем тремя различными длинами. Две задачи эквивалентны при линейном соответствии между единичным интервалом и окружностью окружности и соответствии между действительным числом и углом . ^{[2] [3] [4]} ${\displaystyle n}$ ${\displaystyle \theta ,2\theta ,\dots ,n\theta }$ ${\displaystyle \alpha }$ ${\displaystyle n}$ ${\displaystyle \alpha ,2\alpha ,\dots ,n\alpha }$ ${\displaystyle \alpha }$ ${\displaystyle \theta =2\pi \alpha }$

Приложения

Рост растений

Вид стебля растения с торца, в котором последовательные листья разделены золотым углом.

При изучении филлотаксиса , расположения листьев на стеблях растений, было замечено, что каждый последующий лист на стеблях многих растений повернут относительно предыдущего листа на золотой угол , приблизительно 137,5°. Было высказано предположение, что этот угол максимизирует способность листьев растения собирать солнце. ^[5] Если посмотреть с торца на стебель растения, выросший таким образом, то будет максимум три различных угла между двумя листьями, которые являются последовательными в циклическом порядке, заданном этим видом с торца. ^[6]

Точки, расположенные в золотом углу спирали Ферма (в центре), расположены более равномерно, чем в других углах.

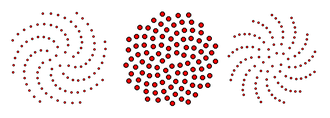
Например, на рисунке наибольший из этих трех углов встречается три раза: между листьями с номерами 3 и 6, между листьями 4 и 7 и между листьями 5 и 8. Второй по величине угол встречается пять раз: между листьями 6 и 1, 9 и 4, 7 и 2, 10 и 5, и 8 и 3. А наименьший угол встречается только дважды: между листьями 1 и 9 и между листьями 2 и 10. Феномен наличия трех типов отдельных зазоров зависит только от того факта, что модель роста использует постоянный угол поворота, а не от отношения этого угла к золотому сечению ; то же самое явление произошло бы для любого другого угла поворота, а не только для золотого угла. Однако другие свойства этой модели роста зависят от золотого сечения. Например, тот факт, что золотое сечение является плохо аппроксимируемым числом, подразумевает, что точки, расположенные под этим углом вдоль спирали Ферма (как это происходит в некоторых моделях роста растений), образуют множество Делоне ; Интуитивно это означает, что они расположены равномерно. ^[7]

Теория музыки

Тоны пифагорейского строя как точки хроматического круга . Края указывают на чистые квинты, используемые для построения строя; два более длинных промежутка между последовательными точками представляют полутоны , а короткий промежуток, где додекаграмма не закрывается, является пифагорейской запятой .

В теории музыки музыкальный интервал описывает соотношение частот между двумя музыкальными тонами . Интервалы обычно считаются консонансными или гармоничными, когда они являются соотношением двух небольших целых чисел; например, октава соответствует соотношению 2:1, в то время как чистая квинта соответствует соотношению 3:2. ^[8] Два тона обычно считаются эквивалентными, когда они отличаются на целое число октав; эта эквивалентность может быть представлена ​​геометрически хроматическим кругом , точки которого представляют классы эквивалентных тонов. Математически этот круг можно описать как единичный круг в комплексной плоскости , и точка на этом круге, которая представляет данный тон, может быть получена путем отображения частоты в комплексное число . Интервал с соотношением соответствует углу между точками на этом круге, что означает, что два музыкальных тона отличаются на заданный интервал, когда их две точки на круге отличаются на этот угол. Например, эта формула дает (целый круг) в качестве угла, соответствующего октаве. Поскольку 3/2 не является рациональной степенью двойки , угол на хроматическом круге, представляющий чистую квинту, не является рациональным кратным , и аналогично другие распространенные музыкальные интервалы, отличные от октавы, не соответствуют рациональным углам. ^[9] ${\displaystyle \nu }$ ${\textstyle \exp(2\pi i\log _{2}\nu )}$ ${\displaystyle \rho }$ ${\displaystyle 2\pi \log _{2}\rho }$ ${\displaystyle 2\pi }$ ${\displaystyle 2\pi }$

Система настройки — это набор тонов, используемых для сочинения и исполнения музыки. Например, равномерная темперация, обычно используемая для фортепиано, — это система настройки, состоящая из 12 тонов, равномерно распределенных по хроматическому кругу. Некоторые другие системы настройки не распределяют свои тоны равномерно, а вместо этого генерируют их некоторым количеством последовательных кратных заданного интервала. Примером является пифагорейская настройка , которая построена таким образом из двенадцати тонов, генерируемых как последовательные кратные чистой квинты в круге квинт . Иррациональный угол, образованный на хроматическом круге чистой квинтой, близок к 7/12 круга, и поэтому двенадцать тонов пифагорейской настройки близки, но не совпадают с двенадцатью тонами равномерной темперации, которые можно было бы генерировать таким же образом, используя угол ровно в 7/12 круга. ^[10] Вместо того, чтобы располагаться под углами, равными точно 1/12 окружности, как это было бы с тонами равномерной темперации, тоны пифагорейской настройки разделены интервалами в два разных угла, близкими, но не точно равными 1/12 окружности, что представляет собой два разных типа полутонов . ^[11] Если бы пифагорейская система настройки была расширена еще на одну чистую квинту, до набора из 13 тонов, то последовательность интервалов между ее тонами включала бы третий, гораздо более короткий интервал, пифагорейскую комму . ^[12]

В этом контексте теорема о трех промежутках может быть использована для описания любой системы настройки, которая генерируется таким образом последовательными кратными одного интервала. Некоторые из этих систем настройки (например, равномерная темперация) могут иметь только один интервал, разделяющий ближайшие пары тонов, а некоторые (например, пифагорейская настройка) могут иметь только два различных интервала, разделяющих тоны, но теорема о трех промежутках подразумевает, что всегда существует не более трех различных интервалов, разделяющих тоны. ^{[13] [14]}

Зеркальное отражение

В слове Фибоначчи , примере слова Штурма , есть четыре различных подпоследовательности длины 3 (в порядке слева направо): 010, 100, 001 и 101.

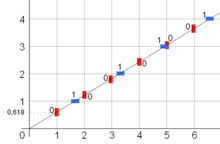
Слово Штурма — это бесконечные последовательности из двух символов (например, «H» и «V»), описывающие последовательность горизонтальных и вертикальных отражений светового луча внутри зеркального квадрата, начинающегося вдоль линии иррационального наклона. Эквивалентно, та же последовательность описывает последовательность горизонтальных и вертикальных линий целочисленной сетки, которые пересекаются начальной линией. Одно свойство, которым обладают все такие последовательности, состоит в том, что для любого положительного целого числа n последовательность имеет ровно n + 1 различных последовательных подпоследовательностей длины n . Каждая подпоследовательность встречается бесконечно часто с определенной частотой, и теорема о трех промежутках подразумевает, что эти n + 1 подпоследовательности встречаются не более чем с тремя различными частотами. Если имеется три частоты, то наибольшая частота должна быть равна сумме двух других. Одно доказательство этого результата включает разбиение y -пересечений начальных линий (по модулю 1) на n + 1 подынтервалов, в пределах которых начальные n элементов последовательности одинаковы, и применение теоремы о трех промежутках к этому разбиению. ^{[15] [16]}

История и доказательства

Теорема о трех щелях была выдвинута Гуго Штейнхаусом , и ее первые ^[17] доказательства были найдены в конце 1950-х годов Верой Т. Шош , ^[18] Яношем Шураньи  [hu] , ^[19] и Станиславом Сверчковским . ^[20] Более поздние исследователи опубликовали дополнительные доказательства, ^[21] обобщающие этот результат на более высокие размерности ^{[22] [23] [24] [25]} и связывающие его с такими темами, как непрерывные дроби , ^{[4] [26]} симметрии и геодезические римановых многообразий , ^[27] эргодическая теория , ^[28] и пространство плоских решеток . ^[3] Майеро (2000) формализует доказательство с помощью интерактивного доказательного устройства теорем Coq . ^[2]

Следующее простое доказательство принадлежит Фрэнку Лянгу. Пусть θ будет углом поворота, порождающим множество точек как некоторое количество последовательных кратных θ на окружности. Определим зазор как дугу A окружности, которая простирается между двумя соседними точками данного множества, и определим зазор как жесткий, если его конечные точки встречаются позже в последовательности кратных θ, чем любой другой зазор той же длины. Из этого определения следует, что каждый зазор имеет ту же длину, что и жесткий зазор. Если A является жестким зазором, то A + θ не является зазором, потому что он имеет ту же длину и будет на один шаг позже. Единственные способы, которыми это может произойти, — это чтобы одна из конечных точек A была последней точкой в ​​последовательности кратных θ (так что соответствующая конечная точка A + θ отсутствует) или чтобы одна из заданных точек попала в A + θ , не давая ей стать зазором. Точка может оказаться в пределах A + θ только в том случае, если она является первой точкой в ​​последовательности кратных θ , поскольку в противном случае ее предшественница в последовательности оказалась бы в пределах A , что противоречит предположению, что A является промежутком. Таким образом, может быть не более трех жестких промежутков, два по обе стороны от последней точки и один, в который приземлилась бы предшественница первой точки (если бы она была частью последовательности). Поскольку существует не более трех жестких промежутков, существует не более трех длин промежутков. ^{[29] [30]}

Связанные результаты

Доказательство Ляна дополнительно показывает, что когда есть ровно три длины промежутка, самая большая длина промежутка является суммой двух других. В этом случае повернутая копия A + θ , которая имеет в себе первую точку, разделена этой точкой на два меньших промежутка, которые должны быть двумя другими промежутками. ^{[29] [30]} Лян также доказывает более общий результат, « теорему о расстоянии», согласно которой объединение различных арифметических прогрессий на окружности имеет не более различных длин промежутков. ^[29] В теореме о трех промежутках существует постоянная граница для отношений между тремя промежутками, если и только если θ /2 π является плохо приближаемым числом . ^[7] ${\displaystyle 3d}$ ${\displaystyle d}$ ${\displaystyle 3d}$

Тесно связанная, но более ранняя теорема, также называемая теоремой о трех промежутках, заключается в том, что если A — любая дуга окружности, то целочисленная последовательность кратных θ , которая попадает в A, имеет не более трех длин промежутков между значениями последовательности. Опять же, если есть три длины промежутков, то один из них является суммой двух других. ^{[31] [32]}

Смотрите также

• Теорема о равнораспределении
• Гипотеза одинокого бегуна

Ссылки

1. Аллуш, Жан-Поль; Шаллит, Джеффри (2003), «2.6 Теорема о трех расстояниях», Автоматические последовательности: теория, приложения, обобщения, Cambridge University Press, стр. 53–55, ISBN 9780521823326
2. Mayero, Micaela (2000), "Теорема о трех зазорах (гипотеза Штейнгауза)", Типы для доказательств и программ: Международный семинар, TYPES'99, Лёкеберг, Швеция, 12–16 июня 1999 г., Избранные статьи , Заметки лекций по информатике, т. 1956, Springer, стр. 162–173, arXiv : cs/0609124 , doi :10.1007/3-540-44557-9_10, ISBN 978-3-540-41517-6, S2CID  3228597
3. Marklof, Jens; Strömbergsson, Andreas (2017), «Теорема о трех зазорах и пространство решеток», The American Mathematical Monthly , 124 (8): 741–745, arXiv : 1612.04906 , doi : 10.4169/amer.math.monthly.124.8.741, hdl : 1983/b5fd0feb-e42d-48e9-94d8-334b8dc24505, JSTOR  10.4169/amer.math.monthly.124.8.741, MR  3706822, S2CID  119670663
4. van Ravenstein, Tony (1988), «Теорема о трех щелях (гипотеза Штейнгауза)», Журнал Австралийского математического общества , Серия A, 45 (3): 360–370, doi : 10.1017/S1446788700031062 , MR  0957201
5. Адам, Джон А. (2011), Математическая прогулка по природе, Princeton University Press, стр. 35–41, ISBN 9781400832903
6. ван Равенштейн, Тони (1987), «Числовые последовательности и филлотаксис», Бюллетень Австралийского математического общества , 36 (2): 333, doi : 10.1017/s0004972700026605
7. Akiyama, Shigeki (март 2020 г.), «Спиральные множества Делоне и теорема о трех расстояниях», Nonlinearity , 33 (5): 2533–2540, arXiv : 1904.10815 , Bibcode : 2020Nonli..33.2533A, doi : 10.1088/1361-6544/ab74ad, S2CID  129945118
8. Хаак, Джоэл К. (1999), «Математика правильной интонации, используемой в музыке Терри Райли», в Сарханги, Реза (ред.), Мосты: математические связи в искусстве, музыке и науке , Юго-западный колледж, Уинфилд, Канзас: Конференция мостов, стр. 101–110, ISBN 0-9665201-1-4
9. Baroin, Gilles; Calvet, André (2019), «Визуализация темпераментов: квадратура круга?», в Montiel, Mariana; Gomez-Martin, Francisco; Agustín-Aquino, Octavio A. (ред.), Mathematics and Computation in Music: 7th International Conference, MCM 2019, Madrid, Spain, June 18–21, 2019, Proceedings , Springer International Publishing, стр. 333–337, doi : 10.1007/978-3-030-21392-3_27, S2CID  184482714
10. Кэри, Норман; Клампитт, Дэвид (октябрь 1989 г.), «Аспекты хорошо сформированных гамм», Music Theory Spectrum , 11 (2): 187–206, doi :10.2307/745935, JSTOR  745935
11. Штром, Рейнхард; Блэкберн, Бонни Дж. , ред. (2001), Музыка как концепция и практика в позднее Средневековье, том 3, часть 1, Новая оксфордская история музыки, Oxford University Press, стр. 252, ISBN 9780198162056
12. Бенсон, Дональд К. (2003), Гладкий камешек: математические исследования, Oxford University Press, стр. 51, ISBN 9780198032977
13. Кэри, Норман (2007), «Связность и одинаковость в хорошо сформированных и попарно хорошо сформированных шкалах», Журнал математики и музыки , 1 (2): 79–98, doi :10.1080/17459730701376743, S2CID  120586231
14. Нарушима, Теруми (2017), Микротональность и системы настройки Эрва Уилсона: отображение гармонического спектра, Routledge Studies in Music Theory, Routledge, стр. 90–91, ISBN 9781317513421
15. Лотер, М. (2002), «Sturmian Words», Algebraic Combinatorics on Words, Кембридж: Cambridge University Press , стр. 40–97, ISBN 978-0-521-81220-7, ЗБЛ  1001.68093. Лотер использует свойство иметь слова длины как определение слов Штурма, а не как следствие определения. Об эквивалентности этого свойства с определением, приведенным здесь, см. Теорему 2.1.13, стр. 51. О трех частотах этих слов см. Теорему 2.2.37, стр. 73. ${\displaystyle d+1}$ ${\displaystyle d}$
16. Алессандри, Паскаль; Берте, Валери (1998), «Три теоремы о расстоянии и комбинаторика слов», L'Enseignement mathématique , 44 (1–2): 103–132, MR  1643286; см. в частности раздел 2.1 «Сложность и частоты кодирования вращений»
17. Хейнс, Алан; Марклоф, Йенс (2020), «Высокомерные задачи Штейнгауза и Слейтера с помощью однородной динамики», Annales Scientifiques de l'École Normale Supérieure , 53 (2): 537–557, arXiv : 1707.04094 , doi : 10.24033/asens.2427, MR  4094564, S2CID  67851217, Первые доказательства этого замечательного факта были опубликованы в 1957 году Сосом, в 1958 году Сурани и в 1959 году Сверчковским.
18. Sós, VT (1958), "О распределении mod 1 последовательности ", Ann. Univ. Sci. Budapest, Eötvös Sect. Math. , 1 : 127–134 ${\displaystyle n\alpha }$
19. Сурани, Дж. (1958), «Über die Anordnung der Vielfachen einer reelen Zahl mod 1», Ann. унив. наук. Будапешт, квартал Этвёш. Математика. , 1 : 107–111
20. Сверчковски, С. (1959), «О последовательных установках дуги на окружности круга», Fundamenta Mathematicae , 46 (2): 187–189, doi : 10.4064/fm-46-2-187-189 , МР  0104651
21. Эти доказательства кратко рассмотрены и классифицированы Марклофом и Стрёмбергссоном (2017), из которых взята следующая классификация этих доказательств и многие из их ссылок.
22. Хэлтон, Джон Х. (1965), «Распределение последовательности », Математические труды Кембриджского философского общества , 61 (3): 665–670, doi :10.1017/S0305004100039013, MR  0202668, S2CID  123400321 ${\displaystyle \{n\xi \}\,(n=0,\,1,\,2,\,\ldots )}$
23. Шевалье, Николя (2007), «Циклические группы и теорема о трех расстояниях», Канадский журнал математики , 59 (3): 503–552, doi : 10.4153/CJM-2007-022-3 , MR  2319157, S2CID  123011205
24. Виджай, Суджит (2008), «Одиннадцати евклидовых расстояний достаточно», Журнал теории чисел , 128 (6): 1655–1661, arXiv : math/0609536 , doi : 10.1016/j.jnt.2007.08.016 , MR  2419185, S2CID  119655772
25. Bleher, Pavel M.; Homma, Youkow; Ji, Lyndon L.; Roeder, Roland KW; Shen, Jeffrey D. (2012), "Расстояния до ближайших соседей на окружности: многомерный случай", Journal of Statistical Physics , 146 (2): 446–465, arXiv : 1107.4134 , Bibcode : 2012JSP...146..446B, doi : 10.1007/s10955-011-0367-8, MR  2873022, S2CID  99723
26. Слейтер, Ноэль Б. (1967), «Пробелы и шаги для последовательности », Математические труды Кембриджского философского общества , 63 (4): 1115–1123, doi :10.1017/S0305004100042195, MR  0217019, S2CID  121496726 ${\displaystyle n\theta {\bmod {1}}}$
27. Бирингер, Ян; Шмидт, Бенджамин (2008), «Теорема о трех пробелах и риманова геометрия», Geometriae Dedicata , 136 : 175–190, arXiv : 0803.1250 , doi : 10.1007/s10711-008-9283-8, MR  2443351, S2CID  6389675
28. Хейнс, Алан; Койвусало, Хенна; Уолтон, Джеймс; Садун, Лоренцо (2016), «Проблемы с зазорами и частоты патчей в разрезах и проектных множествах» (PDF) , Математические труды Кембриджского философского общества , 161 (1): 65–85, Bibcode : 2016MPCPS.161...65H, doi : 10.1017/S0305004116000128, MR  3505670, S2CID  55686324
29. Liang, Frank M. (1979), «Краткое доказательство теоремы о расстоянии», Discrete Mathematics , 28 (3): 325–326, doi : 10.1016/0012-365X(79)90140-7 , MR  0548632 ${\displaystyle 3d}$
30. Shiu, Peter (2018), «Сноска к теореме о трех зазорах», The American Mathematical Monthly , 125 (3): 264–266, doi : 10.1080/00029890.2018.1412210, MR  3768035, S2CID  125810745
31. Слейтер, Н. Б. (1950), «Распределение целых чисел, для которых », Математические труды Кембриджского философского общества , 46 (4): 525–534, doi :10.1017/S0305004100026086, MR  0041891, S2CID  120454265 ${\displaystyle N}$ ${\displaystyle \theta N<\phi }$
32. Флорек, К. (1951), «Une remarque sur la répartition des nombres », Colloquium Mathematicum , 2 : 323–324 ${\displaystyle n\xi \,(\operatorname {mod} 1)}$