
Теория музыкальных множеств предоставляет концепции для категоризации музыкальных объектов и описания их взаимоотношений. Говард Хансон первым разработал многие концепции для анализа тональной музыки. [2] Другие теоретики, такие как Аллен Форте , далее развили теорию для анализа атональной музыки, [3] опираясь на двенадцатитоновую теорию Милтона Бэббита . Концепции теории музыкальных множеств являются очень общими и могут применяться к тональным и атональным стилям в любой системе равномерной темперации, а в некоторой степени и более общо.
Одна из ветвей теории музыкальных множеств занимается коллекциями ( наборами и перестановками ) высот и классов высот ( теория множеств классов высот ), которые могут быть упорядоченными или неупорядоченными и могут быть связаны музыкальными операциями, такими как транспозиция , мелодическая инверсия и дополнение . Некоторые теоретики применяют методы теории музыкальных множеств также к анализу ритма .
Хотя музыкальная теория множеств часто считается связанной с применением математической теории множеств к музыке, между методами и терминологией этих двух направлений существует множество различий. Например, музыканты используют термины транспозиция и инверсия , тогда как математики использовали бы перевод и отражение . Кроме того, там, где музыкальная теория множеств относится к упорядоченным множествам, математика обычно относится к кортежам или последовательностям (хотя математика действительно говорит об упорядоченных множествах , и хотя их можно рассматривать как включающие музыкальный вид в некотором смысле, они гораздо более вовлечены).
Более того, музыкальная теория множеств более тесно связана с теорией групп и комбинаторикой , чем с математической теорией множеств, которая занимается такими вопросами, как, например, различные размеры бесконечно больших множеств. В комбинаторике неупорядоченное подмножество из n объектов, таких как классы высоты тона , называется комбинацией , а упорядоченное подмножество — перестановкой . Музыкальную теорию множеств лучше рассматривать как приложение комбинаторики к теории музыки, чем как раздел математической теории множеств. Ее основная связь с математической теорией множеств заключается в использовании словаря теории множеств для обсуждения конечных множеств.
Фундаментальной концепцией теории музыкальных множеств является (музыкальный) набор, который представляет собой неупорядоченную коллекцию классов высоты тона. [4] Точнее, набор классов высоты тона — это числовое представление, состоящее из отдельных целых чисел (т. е. без дубликатов). [5] Элементы набора могут проявляться в музыке как одновременные аккорды, последовательные тоны (как в мелодии) или и то, и другое. [ необходима ссылка ] Соглашения об обозначениях различаются у разных авторов, но наборы обычно заключаются в фигурные скобки: {}, [6] или квадратные скобки: []. [5]
Некоторые теоретики используют угловые скобки ⟨ ⟩ для обозначения упорядоченных последовательностей, [7] в то время как другие различают упорядоченные наборы, разделяя числа пробелами. [8] Таким образом, можно обозначить неупорядоченный набор классов высоты тона 0, 1 и 2 (соответствующих в этом случае C, C ♯ и D) как {0,1,2}. Упорядоченная последовательность CC ♯ -D будет обозначена как ⟨0,1,2⟩ или (0,1,2). Хотя C считается нулем в этом примере, это не всегда так. Например, произведение (будь то тональное или атональное) с четким центром высоты тона F может быть наиболее полезно проанализировано с F, установленным на ноль (в этом случае {0,1,2} будет представлять F, F ♯ и G. (Чтобы использовать числа для представления нот, см. класс высоты тона .)
Хотя теоретики множеств обычно рассматривают наборы классов равномерно темперированных тонов, можно рассматривать наборы тонов, классы неравномерно темперированных тонов, [ требуется ссылка ] ритмические начала или «классы тактов». [9] [10]
Двухэлементные множества называются диадами , трехэлементные множества — трихордами (иногда «триадами», хотя это легко спутать с традиционным значением слова «триада » ). Множества более высокой мощности называются тетрахордами (или тетрадами), пентахордами (или пентадами), гексахордами (или гексадами), гептахордами (гептадами или, иногда, смешивая латинские и греческие корни, «септахордами» — например, Rahn ), [11] октахордами (октадами), нонахордами (нонадами), декахордами (декадами), ундекахордами и, наконец, додекахордами .
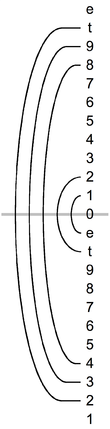
Базовыми операциями, которые могут быть выполнены над множеством, являются транспозиция и инверсия . Множества, связанные транспозицией или инверсией, называются транспозиционно связанными или инверсионно связанными и принадлежат к одному и тому же классу множеств . Поскольку транспозиция и инверсия являются изометриями пространства классов высоты тона, они сохраняют интервальную структуру множества, даже если они не сохраняют музыкальный характер (т. е. физическую реальность) элементов множества. [ необходима цитата ] Это можно считать центральным постулатом теории музыкальных множеств. На практике теоретико-множественный музыкальный анализ часто состоит в выявлении неочевидных транспозиционных или инверсионных отношений между множествами, обнаруженными в произведении.
Некоторые авторы также рассматривают операции дополнения и умножения . Дополнение множества X — это множество, состоящее из всех классов высоты тона, не содержащихся в X. [12] Произведение двух классов высоты тона — это произведение их чисел классов высоты тона по модулю 12. Поскольку дополнение и умножение не являются изометриями пространства классов высоты тона, они не обязательно сохраняют музыкальный характер объектов, которые они преобразуют. Другие авторы, такие как Аллен Форте, подчеркивали Z-отношение , которое получается между двумя множествами, которые разделяют одно и то же общее содержимое интервала или вектор интервала , но не являются транспозиционно или инверсионно эквивалентными. [13] Другое название для этого отношения, используемое Хансоном, [14] — «изомерное». [15]
Операции над упорядоченными последовательностями классов высоты тона также включают транспозицию и инверсию, а также ретроградацию и вращение . Ретроградация упорядоченной последовательности меняет порядок ее элементов на обратный. Вращение упорядоченной последовательности эквивалентно циклической перестановке .
Транспонирование и инверсию можно представить как элементарные арифметические операции. Если x — число, представляющее класс высоты тона, его транспонирование на n полутонов записывается как T n = x + n mod 12. Инверсия соответствует отражению относительно некоторой фиксированной точки в пространстве классов высоты тона . Если x — класс высоты тона, инверсия с индексом n записывается как I n = n - x mod 12.
«Чтобы отношение в множестве S было отношением эквивалентности [в алгебре ], оно должно удовлетворять трем условиям: оно должно быть рефлексивным ..., симметричным ... и транзитивным ...». [16] «Действительно, неформальное понятие эквивалентности всегда было частью теории музыки и анализа. Однако теория множеств PC придерживалась формальных определений эквивалентности». [17]
Говорят, что два транспозиционно связанных набора принадлежат к одному и тому же классу транспозиционных наборов (T n ). Говорят, что два набора, связанных транспозицией или инверсией, принадлежат к одному и тому же классу транспозиционных/инверсионных наборов (инверсия записывается как T n I или I n ). Наборы, принадлежащие к одному и тому же классу транспозиционных наборов, звучат очень похоже; в то время как наборы, принадлежащие к одному и тому же классу транспозиционных/инверсионных наборов, могут включать два аккорда одного и того же типа, но в разных тональностях, которые будут менее похожи по звучанию, но, очевидно, все еще будут ограниченной категорией. Из-за этого музыкальные теоретики часто считают классы наборов основными объектами музыкального интереса.
Существует два основных соглашения для наименования классов равномерно темперированных наборов. Один, известный как число Форте , происходит от Аллена Форте, чья работа «Структура атональной музыки» (1973) является одной из первых работ в теории музыкальных наборов. Форте предоставил каждому классу наборов номер в форме c – d , где c указывает мощность набора, а d — порядковый номер. [18] Таким образом, хроматический трихорд {0, 1, 2} принадлежит классу наборов 3–1, что указывает на то, что это первый класс наборов из трех нот в списке Форте. [19] Увеличенный трихорд {0, 4, 8} получает метку 3–12, которая оказывается последним трихордом в списке Форте.
Основные критические замечания к номенклатуре Форте следующие: (1) Метки Форте произвольны и их трудно запомнить, и на практике часто проще просто перечислить элемент класса набора; (2) Система Форте предполагает равномерную темперацию и не может быть легко расширена для включения диатонических наборов, наборов высоты тона (в отличие от наборов класса высоты тона), мультинаборов или наборов в других системах настройки; (3) Оригинальная система Форте считает, что инверсионно связанные наборы принадлежат к одному и тому же классу набора. Это означает, что, например, мажорное трезвучие и минорное трезвучие считаются одним и тем же набором.
Западная тональная музыка на протяжении столетий считала мажор и минор, а также обращения аккордов существенно разными. Они действительно создают совершенно разные физические объекты. Игнорирование физической реальности звука является очевидным ограничением атональной теории. Однако была сделана защита, что теория не была создана для того, чтобы заполнить вакуум, в котором существующие теории неадекватно объясняли тональную музыку. Скорее, теория Форте используется для объяснения атональной музыки, где композитор изобрел систему, в которой различие между {0, 4, 7} (называемой «мажором» в тональной теории) и ее обращением {0, 3, 7} (называемым «минором» в тональной теории) может быть неактуальным.
Вторая система обозначений маркирует множества в терминах их нормальной формы , которая зависит от концепции нормального порядка . Чтобы привести множество в нормальный порядок, упорядочьте его как восходящую шкалу в пространстве классов высоты тона, которое охватывает менее октавы. Затем циклически переставляйте его, пока его первая и последняя ноты не будут максимально близки друг к другу. В случае лиг минимизируйте расстояние между первой и предпоследней нотой. (В случае лиг здесь минимизируйте расстояние между первой и предпоследней нотой и т. д.) Таким образом, {0, 7, 4} в нормальном порядке — это {0, 4, 7}, тогда как {0, 2, 10} в нормальном порядке — это {10, 0, 2}. Чтобы привести множество к нормальной форме, начните с приведения его в нормальный порядок, а затем транспонируйте его так, чтобы его первый класс высоты тона был равен 0. [20] Математики и специалисты по информатике чаще всего упорядочивают комбинации, используя либо алфавитный порядок, либо двоичный (по основанию два) порядок, либо код Грея , каждый из которых приводит к различным, но логичным нормальным формам. [ необходима ссылка ]
Поскольку транспозиционно связанные множества имеют одну и ту же нормальную форму, нормальные формы можно использовать для обозначения классов множеств T n .
Чтобы определить класс набора T n /I n :
Полученный набор обозначает класс набора T n /I n исходного набора .
Число различных операций в системе, которые отображают множество в себя, является степенью симметрии множества . [21] Степень симметрии «определяет число операций, которые сохраняют неупорядоченные наборы элементов разбиения; она сообщает степень, в которой наборы классов высоты этого разбиения отображаются друг на друга (или друг на друга) при транспозиции или инверсии». [22] Каждое множество имеет по крайней мере одну симметрию, так как оно отображается на себя при операции тождества T 0 . [23] Транспозиционно симметричные множества отображаются на себя для T n , где n не равно 0 (mod 12). Инверсионно симметричные множества отображаются на себя при T n I. Для любого заданного типа T n /T n I все множества имеют одинаковую степень симметрии. Число различных множеств в типе равно 24 (общее число операций, транспозиции и инверсии, для n = 0 через 11), деленное на степень симметрии типа T n /T n I.
Транспозиционно симметричные наборы либо делят октаву поровну, либо могут быть записаны как объединение наборов одинакового размера, которые сами делят октаву поровну. Инверсионно симметричные аккорды инвариантны относительно отражений в пространстве классов высоты тона. Это означает, что аккорды могут быть упорядочены циклически так, что ряд интервалов между последовательными нотами будет таким же, как при прямом, так и при обратном чтении. Например, в циклическом порядке (0, 1, 2, 7) интервал между первой и второй нотой равен 1, интервал между второй и третьей нотой равен 1, интервал между третьей и четвертой нотой равен 5, а интервал между четвертой нотой и первой нотой равен 5. [24]
Ту же последовательность получим, если начать с третьего элемента ряда и двигаться назад: интервал между третьим элементом ряда и вторым равен 1; интервал между вторым элементом ряда и первым равен 1; интервал между первым элементом ряда и четвертым равен 5; и интервал между последним элементом ряда и третьим элементом равен 5. Таким образом, между T 0 и T 2 I найдена симметрия, и в классе эквивалентности T n /T n I имеется 12 множеств. [24]
Источники