Тепловая машина Карно

Осевое сечение тепловой машины Карно. На этой диаграмме *abcd* — цилиндрический сосуд, cd — подвижный поршень , а A и B — тела постоянной температуры. Сосуд может быть помещен в контакт с любым телом или удален от обоих (как здесь). ^[1]

Тепловая машина Карно [ ^2] — это теоретическая тепловая машина , работающая по циклу Карно . Базовая модель этой машины была разработана Николя Леонаром Сади Карно в 1824 году. Модель машины Карно была графически расширена Бенуа Полем Эмилем Клапейроном в 1834 году и математически исследована Рудольфом Клаузиусом в 1857 году, работа, которая привела к фундаментальной термодинамической концепции энтропии . Машина Карно — самая эффективная тепловая машина, которая теоретически возможна. ^[3] Эффективность зависит только от абсолютных температур горячих и холодных тепловых резервуаров, между которыми она работает.

Тепловой двигатель действует, перенося энергию из теплого региона в холодный регион пространства и, в процессе, преобразуя часть этой энергии в механическую работу . Цикл также может быть обратным. Система может подвергаться воздействию внешней силы, и в процессе она может переносить тепловую энергию из более холодной системы в более теплую, тем самым действуя как холодильник или тепловой насос , а не как тепловой двигатель.

Каждая термодинамическая система существует в определенном состоянии . Термодинамический цикл происходит, когда система проходит через ряд различных состояний и в конце концов возвращается в исходное состояние. В процессе прохождения этого цикла система может выполнять работу над своим окружением, тем самым действуя как тепловой двигатель.

Двигатель Карно — это теоретическая конструкция, полезная для исследования пределов эффективности других тепловых двигателей. Однако реальный двигатель Карно было бы совершенно непрактично построить.

Диаграмма Карно

На соседней диаграмме из работы Карно 1824 года « Размышления о движущей силе огня » ^[4] есть «два тела A и B , каждое из которых поддерживается при постоянной температуре, причем температура A выше, чем температура B. Эти два тела, которым мы можем давать или от которых мы можем отнимать тепло, не вызывая изменения их температур, выполняют функции двух неограниченных резервуаров теплорода . Мы назовем первое печью, а второе холодильником». ^[5] Затем Карно объясняет, как мы можем получить движущую силу , т. е. «работу», перенося определенное количество тепла от тела A к телу B. Оно также действует как охладитель и, следовательно, может также действовать как холодильник.

Современная диаграмма

На предыдущем изображении показана оригинальная диаграмма поршня и цилиндра, которую Карно использовал при обсуждении своего идеального двигателя. На рисунке справа показана структурная схема типичного теплового двигателя, такого как двигатель Карно. На схеме «рабочее тело» (система), термин, введенный Клаузиусом в 1850 году, может быть любым жидким или паровым телом, через которое тепло Q может быть введено или передано для производства работы. Карно постулировал, что жидким телом может быть любое вещество, способное расширяться, такое как пар воды, пар спирта, пар ртути, постоянный газ, воздух и т. д. Хотя в те ранние годы двигатели имели ряд конфигураций, обычно Q _H подавался котлом, в котором вода кипела над печью; Q _C обычно удалялся потоком холодной текущей воды в виде конденсатора, расположенного на отдельной части двигателя. Выходная работа, W , передается движением поршня, поскольку он используется для вращения кривошипа, который в свою очередь обычно использовался для приведения в действие шкива, чтобы поднимать воду из затопленных соляных шахт. Карно определил работу как «вес, поднятый на высоту».

цикл Карно

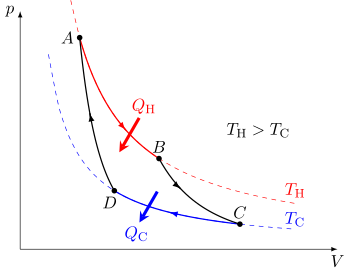
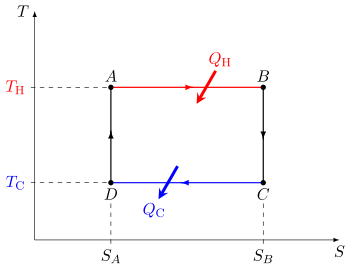
Цикл Карно при работе в качестве теплового двигателя состоит из следующих этапов:

Обратимое изотермическое расширение газа при «горячей» температуре, $T H$ (изотермическое подвод или поглощение тепла). На этом этапе (от $A$ до $B$ ) газу позволяют расширяться, и он выполняет работу над окружающей средой. Температура газа (системы) не меняется в ходе процесса, и, таким образом, расширение является изотермическим. Расширение газа происходит за счет поглощения тепловой энергии $Q H$ и энтропии $Δ S H = Q H / T H$ из высокотемпературного резервуара.
Изоэнтропическое ( обратимое адиабатическое ) расширение газа (изоэнтропическая выходная работа). Для этого шага (от $B$ до $C$ ) поршень и цилиндр считаются теплоизолированными, поэтому они не получают и не теряют тепло. Газ продолжает расширяться, совершая работу над окружающей средой и теряя эквивалентное количество внутренней энергии. Расширение газа заставляет его охлаждаться до «холодной» температуры, $T C.$ Энтропия остается неизменной.
Обратимое изотермическое сжатие газа при «холодной» температуре, $T C$ (изотермический отвод тепла) ( от $C$ до $D$ ). Теперь газ подвергается воздействию резервуара с холодной температурой, в то время как окружающая среда выполняет работу над газом, сжимая его (например, посредством обратного сжатия поршня), в то же время вызывая выделение некоторого количества отработанного тепла $Q C < 0$ (со стандартным соглашением знаков для тепла ) и энтропии $Δ S C = Q C / T C < 0$ из газа в резервуар с низкой температурой. (По величине это то же самое количество энтропии, поглощенное на этапе 1. Энтропия уменьшается при изотермическом сжатии, поскольку множественность системы уменьшается с объемом.) По величине работа по рекомпрессии, выполняемая окружающей средой на этом этапе, меньше работы, выполняемой окружающей средой на этапе 1, поскольку она происходит при более низком давлении из-за более низкой температуры (т. е. сопротивление сжатию ниже на этапе 3, чем сила расширения на этапе 1). Чтобы объяснить это поведение , мы можем обратиться к первому закону термодинамики: $Δ U = W + Q.$
Изоэнтропическое сжатие газа (изоэнтропическая работа) ( $D$ - $A$ ). Опять же, предполагается, что поршень и цилиндр теплоизолированы, а резервуар с холодной температурой удален. На этом этапе окружающая среда продолжает выполнять работу по дальнейшему сжатию газа, и теперь, когда теплоотвод удален, температура и давление повышаются. Эта дополнительная работа увеличивает внутреннюю энергию газа, сжимая его и вызывая повышение температуры до $T H$ . Энтропия остается неизменной. В этот момент газ находится в том же состоянии, что и в начале этапа 1.

Теорема Карно

Теорема Карно является формальным утверждением этого факта: ни один двигатель, работающий между двумя тепловыми резервуарами, не может быть более эффективным, чем двигатель Карно, работающий между теми же резервуарами.

$\eta _{I}={\frac {W}{Q_{\mathrm {H} }}}=1-{\frac {T_{\mathrm {C} }}{T_{\mathrm {H} }}}$

Объяснение

Эта максимальная эффективность $η I$ определяется, как указано выше:

$W$ — работа, совершаемая системой (энергия, выходящая из системы в виде работы),
$Q H$ — тепло, поступающее в систему (тепловая энергия, поступающая в систему),
$T C$ — абсолютная температура холодного резервуара, а
$T H$ — абсолютная температура горячего резервуара.

Следствие из теоремы Карно гласит: Все обратимые двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны.

Легко показать, что эффективность $η$ максимальна, когда весь циклический процесс является обратимым процессом . Это означает, что полная энтропия системы и окружающей среды (энтропии горячей печи, «рабочего тела» тепловой машины и холодного поглотителя) остается постоянной, когда «рабочее тело» завершает один цикл и возвращается в исходное состояние. (В общем и более реалистичном случае необратимого процесса полная энтропия этой комбинированной системы увеличилась бы.)

Поскольку «рабочая жидкость» возвращается в то же состояние после одного цикла, а энтропия системы является функцией состояния, то изменение энтропии системы «рабочая жидкость» равно 0. Таким образом, это означает, что общее изменение энтропии печи и раковины равно нулю, чтобы процесс был обратимым, а эффективность двигателя была максимальной. Этот вывод выполняется в следующем разделе.

Коэффициент полезного действия (КПД) теплового двигателя является величиной, обратной его КПД.

Эффективность реальных тепловых двигателей

Для реального теплового двигателя полный термодинамический процесс, как правило, необратим. Рабочая жидкость возвращается в исходное состояние после одного цикла, и, таким образом, изменение энтропии жидкостной системы равно 0, но сумма изменений энтропии в горячем и холодном резервуаре в этом одном циклическом процессе больше 0.

Внутренняя энергия жидкости также является переменной состояния, поэтому ее общее изменение за один цикл равно 0. Таким образом, общая работа, выполненная системой $W,$ равна чистому теплу, переданному в систему, сумме > 0 принятого и отданного отработанного тепла < 0: ^[6] $Q_{\text{H}}$ $Q_{\text{C}}$

Для реальных двигателей этапы 1 и 3 цикла Карно, в которых тепло поглощается «рабочим телом» из горячего резервуара и отдается им в холодный резервуар соответственно, уже не остаются идеально обратимыми, и при теплообмене возникает разность температур между температурой резервуара и температурой жидкости.

При передаче тепла от горячего резервуара к жидкости, жидкость будет иметь несколько более низкую температуру, чем , и процесс для жидкости не обязательно может оставаться изотермическим. Пусть будет полным изменением энтропии жидкости в процессе поглощения тепла. $T_{\text{H}}$ $T_{\text{H}}$ $\Delta S_{\text{H}}$

где температура жидкости $T$ всегда немного меньше , в этом процессе. $T_{\text{H}}$

Итак, получим:

Аналогично, в момент подачи тепла из жидкости в холодный резервуар, для величины полного изменения энтропии < 0 жидкости в процессе отдачи тепла, будет иметь место: $\Delta S_{\text{C}}$

где в ходе этого процесса передачи тепла холодному резервуару температура жидкости $T$ всегда немного больше . $T_{\text{C}}$

Мы рассмотрели здесь только величину изменения энтропии. Поскольку общее изменение энтропии жидкой системы для циклического процесса равно 0, мы должны иметь

Предыдущие три уравнения, а именно (3), (4), (5), подставляем в (6), чтобы получить: ^[7]

Для [ΔSh ≥ (Qh/Th)] +[ΔSc ≥ (Qc/Tc)] = 0

[ΔSh ≥ (Qh/Th) ] = - [ΔSc ≥ (Qc/Tc)]

= [-ΔSc ≤ (-Qc/Tc) ]

это по крайней мере (Qh/Th) ≤ (-Qc/Tc)

Уравнения ( 2 ) и ( 7 ) объединяются, чтобы дать

Для вывода этого шага необходимо, чтобы два адиабатических процесса продемонстрировали свойство изоэнтропического процесса, поскольку отношение изменяющихся объемов двух изотермических процессов одинаково.

Самое важное, поскольку два адиабатических процесса представляют собой объемные работы без потери тепла, и поскольку соотношение изменений объема для этих двух процессов одинаково, то и работы для этих двух адиабатических процессов одинаковы, но направлены в противоположные стороны, а именно, одно направление — это работа, выполняемая системой, а другое — работа, выполняемая над системой; следовательно, тепловой КПД касается только количества работы, выполняемой поглощенным теплом, по сравнению с количеством тепла, поглощаемого системой.

Следовательно, (W/Qh) = (Qh - Qc) / Qh

= 1 - (Qc/Qh)

= 1 - (Тc/Тh)

И, из (7)

(Qh/Th) ≤ (-Qc/Tc) здесь Qc меньше 0 (выделение тепла)

(Tc/Th) ≤ (-Qc/Qh)

-(Tc/Th) ≥ (Qc/Qh)

1+ [-(Tc/Th)] ≥ 1+ (Qc/Qh)

1 - (Tc/Th) ≥ (Qh + Qc)/Qh здесь Qc<0,

1 - (Tc/Th) ≥ (Qh - Qc)/Qh

1 - (Tc/Th) ≥ W/Qh

Следовательно,

где — эффективность реального двигателя, а — эффективность двигателя Карно, работающего между теми же двумя резервуарами при температурах и . Для двигателя Карно весь процесс «обратим», и уравнение ( 7 ) является равенством. Следовательно, эффективность реального двигателя всегда меньше, чем у идеального двигателя Карно. $\eta ={\frac {W}{Q_{\text{H}}}}$ $\eta _{\text{I}}$ $T_{\text{H}}$ $T_{\text{C}}$

Уравнение ( 7 ) означает, что общая энтропия системы и окружающей среды (жидкости и двух резервуаров) увеличивается для реального двигателя, поскольку (в анализе на основе окружающей среды) прирост энтропии холодного резервуара, втекающего в него при фиксированной температуре , больше, чем потеря энтропии горячего резервуара, вытекающего из него при фиксированной температуре . Неравенство в уравнении ( 7 ) по сути является утверждением теоремы Клаузиуса . $Q_{\text{C}}$ $T_{\text{C}}$ $Q_{\text{H}}$ $T_{\text{H}}$

Согласно второй теореме, «КПД двигателя Карно не зависит от природы рабочего тела».

Двигатель Карно и Рудольф Дизель

В 1892 году Рудольф Дизель запатентовал двигатель внутреннего сгорания, вдохновленный двигателем Карно. Дизель знал, что двигатель Карно — это идеал, который невозможно построить, но он думал, что изобрел рабочее приближение. Его принцип был несостоятельным, но в борьбе за его реализацию он разработал практический дизельный двигатель .

Концептуальная проблема заключалась в том, как достичь изотермического расширения в двигателе внутреннего сгорания, поскольку сжигание топлива при самой высокой температуре цикла только повышало бы температуру еще больше. Запатентованное решение Дизеля было: достигнув самой высокой температуры просто сжатием воздуха, добавить небольшое количество топлива с контролируемой скоростью, так что нагрев, вызванный сжиганием топлива, будет компенсироваться охлаждением, вызванным расширением воздуха при движении поршня. Следовательно, все тепло от топлива будет преобразовано в работу во время изотермического расширения, как того требует теорема Карно.

Для того, чтобы эта идея сработала, необходимо было сжечь небольшую массу топлива в огромной массе воздуха. Дизель первым предложил работающий двигатель, который сжимал воздух до 250 атмосфер при 800 °C (1450 °F), а затем циклически доходил до одной атмосферы при 20 °C (50 °F). Однако это было далеко за пределами технологических возможностей того времени, поскольку подразумевало степень сжатия 60:1. Такой двигатель, если бы его удалось построить, имел бы КПД 73%. (Для сравнения, лучшие паровые двигатели его времени достигли 7%.)

Соответственно, Дизель стремился к компромиссу. Он подсчитал, что если бы он снизил пиковое давление до менее амбициозных 90 атмосфер, он бы пожертвовал только 5% теплового КПД . Ища финансовую поддержку, он опубликовал «Теорию и конструкцию рациональной тепловой машины, которая могла бы занять место паровой машины и всех известных в настоящее время двигателей внутреннего сгорания» (1893). Одобренный научным мнением, включая лорда Кельвина , он получил поддержку Круппа и Maschinenfabrik Augsburg . Он цеплялся за цикл Карно как за символ. Но годы практической работы не привели к созданию изотермического двигателя внутреннего сгорания, да и не могли бы, поскольку для этого требуется такое огромное количество воздуха, что он не может развить достаточно мощности для его сжатия. Кроме того, контролируемый впрыск топлива оказался нелегким делом.

Тем не менее, дизельный двигатель медленно развивался в течение 25 лет, чтобы стать практичным воздушным двигателем с высокой степенью сжатия, в котором топливо впрыскивается ближе к концу такта сжатия и воспламеняется от тепла сжатия, что к 1969 году позволило достичь КПД в 40%. ^[8]

Как макроскопическая конструкция

Тепловая машина Карно, в конечном счете, является теоретической конструкцией, основанной на идеализированной термодинамической системе . На практическом уровне человеческого масштаба цикл Карно оказался ценной моделью, как в продвижении разработки дизельного двигателя . Однако в макроскопическом масштабе ограничения, накладываемые предположениями модели, доказывают ее непрактичность и, в конечном счете, неспособность выполнять какую-либо работу . ^[9] Таким образом, согласно теореме Карно , двигатель Карно можно рассматривать как теоретический предел макроскопических масштабов тепловых машин, а не как любое практическое устройство, которое когда-либо могло быть построено. ^[10]

Например, для изотермической части расширения цикла Карно следующие бесконечно малые условия должны быть выполнены одновременно на каждом шаге расширения: ^[11]

Температура горячего резервуара T _H бесконечно выше температуры газа системы T, поэтому поток тепла (передача энергии) от горячего резервуара к газу осуществляется без увеличения T (посредством бесконечно малой работы над окружающей средой со стороны газа в качестве еще одной передачи энергии); если T _H значительно выше T , то T может быть неравномерной по всему газу, поэтому система отклонится от теплового равновесия, а также не будет обратимым процессом (т. е. не циклом Карно), или T может заметно увеличиться, поэтому это не будет изотермическим процессом.
Сила, приложенная извне к поршню (противоположная внутренней силе, действующей на поршень со стороны газа), должна быть бесконечно мало уменьшена извне. Без этой помощи было бы невозможно следовать кривой PV (давление-объем) газа вниз при постоянном значении T, поскольку следование этой кривой означает, что сила между газом и поршнем уменьшается ( P уменьшается) по мере расширения объема (поршень движется наружу). Если эта помощь настолько сильна, что расширение объема становится значительным, система может отклониться от теплового равновесия , и процесс перестанет быть обратимым (и, следовательно, не циклом Карно).

Такие «бесконечно малые» требования, как эти (и другие), приводят к тому, что цикл Карно занимает бесконечное количество времени , делая производство работы невозможным. ^[9]

Другие практические требования, которые делают цикл Карно непрактичным для реализации, включают в себя точное управление газом и идеальный тепловой контакт с окружающей средой (включая резервуары с высокой и низкой температурой). ^{[ необходима цитата ]}

Примечания

^ Рисунок 1 в Carnot (1824, стр. 17) и Carnot (1890, стр. 63). На схеме диаметр сосуда достаточно велик, чтобы перекрыть пространство между двумя телами, но в модели сосуд никогда не контактирует с обоими телами одновременно. Также на схеме показан немаркированный осевой стержень, прикрепленный к внешней стороне поршня.
^ Во французском языке Карно использует machine à feu , что Терстон переводит как тепловая машина или паровая машина . В сноске Карно различает паровую машину ( machine à vapeur ) от тепловой машины вообще. (Carnot, 1824, стр. 5 и Carnot, 1890, стр. 43)
^ "КПД Карно | EGEE 102: Энергосбережение и защита окружающей среды". www.e-education.psu.edu . Получено 24.01.2022 .
^ «Иногда переводится как Размышления о движущей силе тепла».
↑ Английский перевод Терстона (Карно, 1890, стр. 51-52).
^ Планк, М. (1945). Трактат по термодинамике . Dover Publications. стр. 90. §90, уравнения (39) и (40)
^ Ферми, Э. (1956). Термодинамика . Dover Publications (все еще в печати). стр. 47. ниже ур. (63)
↑ Брайант, Линвуд (август 1969 г.). «Рудольф Дизель и его рациональный двигатель». Scientific American . 221 (2): 108–117. Bibcode : 1969SciAm.221b.108B. doi : 10.1038/scientificamerican0869-108. JSTOR 24926442.
^ ab Liu, Hang; Meng, Xin-He (2017-08-18). "Влияние темной энергии на эффективность заряженных черных дыр AdS как тепловых двигателей". The European Physical Journal C . 77 (8): 556. arXiv : 1704.04363 . doi :10.1140/epjc/s10052-017-5134-9. ISSN 1434-6052. ...так как тепловая машина Карно, установление верхней границы эффективности тепловой машины является идеальным, обратимым двигателем, один цикл которого должен быть выполнен за бесконечное время, что непрактично, и поэтому двигатель Карно имеет нулевую мощность.
^ Бененти, Джулиано; Казати, Джулио; Ван, Цзяо (2020). "Мощность, эффективность и колебания в стационарных тепловых двигателях" (PDF) . Physical Review E. 102 ( 4). Однако колебания [температуры резервуара] делают такие двигатели непрактичными.
^ D, Bob (2020-01-15). "Почему газ расширяется в фазе изотермического расширения цикла Карно?". StackExchange . Получено 2022-01-02 .

Внешние ссылки

Эпизод 46. Двигатель природы: Двигатель Карно, часть первая, начиная с простых паровых двигателей. Механическая вселенная . Калтех – через YouTube.

Ссылки

Брайант, Линвуд (август 1969 г.). «Рудольф Дизель и его рациональный двигатель». Scientific American . 221 (2): 108–117. Bibcode : 1969SciAm.221b.108B. doi : 10.1038/scientificamerican0869-108. JSTOR 24926442.
Карно, Сади (1824). Réflexions sur la puissance motrice du feu et sur les cars propres à developper cette puissance (на французском языке). Париж: Башелье.(Первое издание 1824 г.) и (Переиздание 1878 г.)
Карно, Сади (1890). Терстон, Роберт Генри (ред.). Размышления о движущей силе тепла и о машинах, приспособленных для развития этой силы. Нью-Йорк: J. Wiley & Sons.(полный текст издания 1897 г.) (Архивная версия HTML)