В тетраэдрической молекулярной геометрии центральный атом расположен в центре с четырьмя заместителями , которые расположены в углах тетраэдра . Углы связи составляют cos −1 (− 1 ⁄ 3 ) = 109,4712206...° ≈ 109,5°, когда все четыре заместителя одинаковы, как в метане ( CH 4 ) [1] [2] , а также его более тяжелых аналогах . Метан и другие идеально симметричные тетраэдрические молекулы принадлежат к точечной группе T d , но большинство тетраэдрических молекул имеют более низкую симметрию . Тетраэдрические молекулы могут быть хиральными .


Угол связи для симметричной тетраэдрической молекулы, такой как CH 4 , можно рассчитать с помощью скалярного произведения двух векторов . Как показано на диаграмме слева, молекулу можно вписать в куб с четырехвалентным атомом (например, углеродом ) в центре куба, который является началом координат, O. Четыре одновалентных атома (например, водороды) находятся в четырех углах куба (A, B, C, D), выбранных так, чтобы никакие два атома не находились в соседних углах, связанных только одним ребром куба.
Если длина ребра куба выбрана равной 2 единицам, то две связи OA и OB соответствуют векторам a = (1, –1, 1) и b = (1, 1, –1), а угол связи θ является углом между этими двумя векторами. Этот угол может быть вычислен из скалярного произведения двух векторов, определяемого как a • b = || a || || b || cos θ, где || a || обозначает длину вектора a . Как показано на диаграмме, скалярное произведение здесь равно –1, а длина каждого вектора равна √3, так что cos θ = –1/3 и тетраэдрический угол связи θ = arccos (–1/3) ≃ 109,47°.
Альтернативное доказательство с использованием тригонометрии показано на схеме справа.
За исключением практически всех насыщенных органических соединений, большинство соединений Si, Ge и Sn являются тетраэдрическими. Часто тетраэдрические молекулы характеризуются множественной связью с внешними лигандами, как в тетроксиде ксенона (XeO 4 ), перхлорат- ионе ( ClO−4), сульфат- ион ( SO2−4), ион фосфата ( PO3−4). Трифторид тиазила ( SNF 3 ) является тетраэдрическим, с тройной связью серы с азотом. [3]
Другие молекулы имеют тетраэдрическое расположение электронных пар вокруг центрального атома; например, аммиак ( NH 3 ) с атомом азота, окруженным тремя водородами и одной неподеленной парой . Однако обычная классификация рассматривает только связанные атомы, а не неподеленную пару, так что аммиак фактически считается пирамидальным . Углы H–N–H составляют 107°, сокращенные с 109,5°. Это различие объясняется влиянием неподеленной пары, которая оказывает большее отталкивающее воздействие, чем связанный атом. [ необходима цитата ]
Опять же, геометрия широко распространена, особенно для комплексов, где металл имеет конфигурацию d 0 или d 10. Иллюстративные примеры включают тетракис(трифенилфосфин)палладий(0) ( Pd[P(C 6 H 5 ) 3 ] 4 ), карбонил никеля ( Ni(CO) 4 ) и тетрахлорид титана ( TiCl 4 ). Многие комплексы с не полностью заполненными d-оболочками часто являются тетраэдрическими, например, тетрагалогениды железа(II), кобальта(II) и никеля(II).
В газовой фазе одна молекула воды имеет атом кислорода, окруженный двумя атомами водорода и двумя неподеленными парами, а геометрия H 2 O просто описывается как изогнутая , без учета несвязанных неподеленных пар. [ необходима цитата ]
Однако в жидкой воде или во льду неподеленные пары образуют водородные связи с соседними молекулами воды. Наиболее распространенное расположение атомов водорода вокруг кислорода — тетраэдрическое, при котором два атома водорода ковалентно связаны с кислородом, а два других соединены водородными связями. Поскольку водородные связи различаются по длине, многие из этих молекул воды несимметричны и образуют временные нерегулярные тетраэдры между четырьмя связанными с ними атомами водорода. [4]
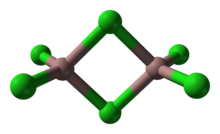
Многие соединения и комплексы принимают битетраэдрические структуры. В этом мотиве два тетраэдра имеют общее ребро. Неорганический полимер дисульфид кремния имеет бесконечную цепочку тетраэдров с общим ребром. В полностью насыщенной углеводородной системе битетраэдрическая молекула C 8 H 6 была предложена в качестве кандидата на молекулу с максимально короткой одинарной углерод-углеродной связью . [5]
Инверсия тетраэдров широко распространена в органической и основной групповой химии. Инверсия Вальдена иллюстрирует стереохимические последствия инверсии у углерода. Инверсия азота в аммиаке также влечет за собой кратковременное образование плоского NH 3 .
Геометрические ограничения в молекуле могут вызвать сильное искажение идеализированной тетраэдрической геометрии. В соединениях, имеющих «перевернутую» тетраэдрическую геометрию у атома углерода, все четыре группы, присоединенные к этому углероду, находятся на одной стороне плоскости. [6] Атом углерода находится на вершине квадратной пирамиды или около нее, а остальные четыре группы — в углах. [7] [8]
Простейшими примерами органических молекул, демонстрирующих перевернутую тетраэдрическую геометрию, являются наименьшие пропелланы , такие как [1.1.1]пропеллан ; или, в более общем смысле, паддланы , [9] и пирамидан ([3.3.3.3]фенестран). [7] [8] Такие молекулы обычно напряжены , что приводит к повышенной реакционной способности.
Тетраэдр также может быть искажен путем увеличения угла между двумя связями. В крайнем случае, происходит уплощение. Для углерода это явление можно наблюдать в классе соединений, называемых фенестранами . [ необходима цитата ]
Несколько молекул имеют тетраэдрическую геометрию без центрального атома. Неорганическим примером является тетрафосфор (P4), который имеет четыре атома фосфора в вершинах тетраэдра, и каждый из них связан с тремя другими. Органическим примером является тетраэдр (C4H4 ) с четырьмя атомами углерода, каждый из которых связан с одним водородом и тремя другими атомами углерода. В этом случае теоретический угол связи C−C−C составляет всего 60° (на практике угол будет больше из-за изогнутых связей ), что представляет большую степень деформации. [ требуется цитата ]