Треугольная бипирамида

Два тетраэдра, соединенные одной гранью

Треугольная бипирамида — это гексаэдр с шестью треугольными гранями, образованный путем присоединения двух тетраэдров лицом к лицу. Эта же форма также известна как треугольная дипирамида ^{[1] [2]} или тригональная бипирамида . ^[3] Если эти тетраэдры правильные, все грани треугольной бипирамиды равносторонние . Это пример дельтаэдра , составного многогранника и тела Джонсона .

Многие многогранники связаны с треугольной бипирамидой, например, похожие формы, полученные из разных подходов, и треугольная призма как ее двойственный многогранник . Приложения треугольной бипирамиды включают тригональную бипирамидальную молекулярную геометрию , которая описывает ее атомный кластер , решение проблемы Томсона и представление систем порядка цвета к восемнадцатому веку.

Особые случаи

Как правильная бипирамида

Как и другие бипирамиды , треугольная бипирамида может быть построена путем присоединения двух тетраэдров лицом к лицу. ^[2] Эти тетраэдры покрывают свое треугольное основание, и полученный многогранник имеет шесть треугольников, пять вершин и девять ребер. ^[3] Треугольная бипирамида называется правильной, если тетраэдры симметрично правильные и обе их вершины находятся на линии, проходящей через центр основания; в противном случае она наклонная . ^{[4] [5]}

График треугольной бипирамиды

Согласно теореме Штейница , граф может быть представлен в виде скелета многогранника, если он является планарным (рёбра графа не пересекаются, но пересекаются в точке) и трёхсвязным графом (одна из любых двух вершин при удалении оставляет связный подграф). Треугольная бипирамида представлена ​​графом с девятью рёбрами, построенным путём добавления одной вершины к вершинам графа -колеса , представляющего тетраэдры . ^{[6] [7]}

Как и другие правильные бипирамиды, треугольная бипирамида имеет трехмерную точечную группу симметрии , диэдральную группу двенадцатого порядка: внешний вид треугольной бипирамиды не меняется при ее повороте на один, две трети и полный угол вокруг оси симметрии (прямой, проходящей через две вершины и центр основания по вертикали), и она имеет зеркальную симметрию с любой биссектрисой основания; она также симметрична при отражении относительно горизонтальной плоскости. ^[8] Треугольная бипирамида является гранетранзитивной , или изоэдральной. ^[9] ${\displaystyle D_{3\mathrm {h} }}$

Как Джонсон твердый

Треугольная бипирамида с правильными гранями вдоль ее развертки

3D-модель треугольной бипирамиды как тела Джонсона

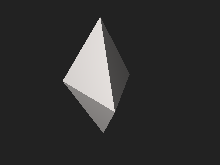
Если тетраэдры правильные, все ребра треугольной бипирамиды равны по длине и образуют равносторонние треугольные грани . Многогранник, у которого в качестве граней используются только равносторонние треугольники, называется дельтаэдром . Существует восемь выпуклых дельтаэдров, один из которых является треугольной бипирамидой с правильными многоугольными гранями. ^[1] Выпуклый многогранник, все грани которого являются правильными многоугольниками, называется телом Джонсона , а каждый выпуклый дельтаэдр является телом Джонсона. Треугольная бипирамида с правильными гранями нумеруется как двенадцатое тело Джонсона . ^[10] Это пример составного многогранника , поскольку он построен путем присоединения двух правильных тетраэдров . ^{[11] [12]} ${\displaystyle J_{12}}$

Площадь поверхности треугольной бипирамиды в шесть раз больше площади каждого треугольника. Ее объем можно вычислить, разрезав ее на два тетраэдра и сложив их объемы. В случае длины ребра это: ^[12] ${\displaystyle A}$ ${\displaystyle V}$ ${\displaystyle a}$ $${\displaystyle {\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}a^{2}&\approx 2.598a^{2},\\V&={\frac {\sqrt {2}}{6}}a^{3}&\approx 0.238a^{3}.\end{aligned}}}$$

Двугранный угол треугольной бипирамиды можно получить, сложив двугранные углы двух правильных тетраэдров. Двугранный угол треугольной бипирамиды между соседними треугольными гранями равен углу правильного тетраэдра: 70,5 градуса. В ребре, где соединены два тетраэдра, двугранный угол соседних треугольников вдвое больше: 141,1 градуса. ^[13]

Связанные многогранники

Граф Голднера–Харари представляет собой треугольную бипирамиду, дополненную тетраэдрами.

Некоторые типы треугольных бипирамид могут быть получены разными способами. Клетоп многогранника — это конструкция, включающая присоединение пирамид. Клетоп треугольной бипирамиды может быть построен из треугольной бипирамиды путем присоединения тетраэдров к каждой из ее граней, заменяя их тремя другими треугольниками; скелет полученного многогранника представляет собой граф Голднера–Харари . ^{[14] [15]} Другой тип треугольной бипирамиды получается путем отсечения ее вершин, процесс, известный как усечение . ^[16]

Бипирамиды являются двойственным многогранником призм . Это означает, что вершины бипирамид соответствуют граням призмы, а ребра между парами вершин одной соответствуют ребрам между парами граней другой; удвоение приводит к исходному многограннику. Треугольная бипирамида является двойственным многогранником треугольной призмы , и наоборот. ^{[17] [3]} Треугольная призма имеет пять граней, девять ребер и шесть вершин с той же симметрией, что и треугольная бипирамида. ^[3]

Приложения

Известное решение задачи Томсона, с одной треугольной бипирамидой

Проблема Томсона касается минимальной энергетической конфигурации заряженных частиц на сфере. Треугольная бипирамида является известным решением в случае пяти электронов, размещая вершины треугольной бипирамиды внутри сферы . ^[18] Это решение поддерживается математически строгим компьютером. ^[19]

Тригонально-бипирамидальная молекулярная геометрия химического соединения может быть описана как атомный кластер треугольной бипирамиды. Эта молекула имеет элемент основной группы без активной неподеленной пары , описанный моделью, которая предсказывает геометрию молекул, известную как теория VSEPR . ^[20] Примерами этой структуры являются пентафторид фосфора и пентахлорид фосфора в газообразной фазе . ^[21]

В теории цвета треугольная бипирамида использовалась для представления трехмерной системы порядка цветов в основных цветах . Немецкий астроном Тобиас Майер в 1758 году писал, что каждая из ее вершин представляет цвет: белый и черный — это верхняя и нижняя осевые вершины соответственно, а остальные вершины — красные, синие и желтые. ^{[22] [23]}

Ссылки

1. Trigg, Charles W. (1978). «Бесконечный класс дельтаэдров». Mathematics Magazine . 51 (1): 55–57. doi :10.1080/0025570X.1978.11976675. JSTOR  2689647. MR  1572246.
2. Rajwade, AR (2001). Выпуклые многогранники с условиями регулярности и третья проблема Гильберта. Тексты и чтения по математике. Hindustan Book Agency. стр. 84. doi :10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
3. King, Robert B. (1994). "Polyhedral Dynamics". В Bonchev, Danail D.; Mekenyan, OG (ред.). Graph Theoretical Approaches to Chemical Reactions . Springer. doi :10.1007/978-94-011-1202-4. ISBN 978-94-011-1202-4.
4. Niu, Wenxin; Xu, Guobao (2011). «Кристаллографический контроль нанокристаллов благородных металлов». Nano Today . 6 (3): 265–285. doi :10.1016/j.nantod.2011.04.006.
5. Александров, Виктор (2017). «Во сколько раз можно увеличить объем выпуклого многогранника изометрическими деформациями?». Beiträge zur Algebra und Geometrie . 58 (3): 549–554. arXiv : 1607.06604 . doi :10.1007/s13366-017-0336-8.
6. Tutte, WT (2001). Теория графов. Cambridge University Press. стр. 113. ISBN 978-0-521-79489-3.
7. Саджад, Вассид; Сардар, Мухаммад С.; Пан, Сян-Фэн (2024). «Вычисление расстояния сопротивления и индекса Кирхгофа цепи треугольной бипирамиды-гексаэдра». Прикладная математика и вычисления . 461 : 1–12. doi :10.1016/j.amc.2023.128313. S2CID  261797042.
8. Александр, Дэниел С.; Кеберлин, Джерелин М. (2014). Элементарная геометрия для студентов колледжей (6-е изд.). Cengage Learning. стр. 403. ISBN 978-1-285-19569-8.
9. Маклин, К. Робин (1990). «Подземелья, драконы и кости». The Mathematical Gazette . 74 (469): 243–256. doi :10.2307/3619822. JSTOR  3619822. S2CID  195047512.
10. Уэхара, Рюхэй (2020). Введение в вычислительное оригами: мир новой вычислительной геометрии. Springer. doi :10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID  220150682.
11. Тимофеенко, АВ (2009). «Выпуклые многогранники с паркетными гранями» (PDF) . Docklady Mathematics . 80 (2): 720–723. doi :10.1134/S1064562409050238.
12. Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. doi :10.1016/0016-0032(71)90071-8. MR  0290245.
13. Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями». Канадский журнал математики . 18 : 169–200. doi : 10.4153/cjm-1966-021-8 . MR  0185507. S2CID  122006114. Zbl  0132.14603.
14. Грюнбаум, Бранко (1967). Выпуклые многогранники . Wiley Interscience. стр. 357.. Та же страница, 2-е изд., Graduate Texts in Mathematics 221, Springer-Verlag, 2003, ISBN 978-0-387-40409-7 . 
15. Эвальд, Гюнтер (1973). «Гамильтоновы схемы в симплициальных комплексах». Геометрии Дедиката . 2 (1): 115–125. дои : 10.1007/BF00149287. S2CID  122755203.
16. Хаджи-Акбари, Амир; Чен, Элизабет Р.; Энгель, Майкл; Глотцер, Шарон К. (2013). «Упаковка и самосборка усеченных треугольных бипирамид». Phys. Rev. E. 88 ( 1): 012127. arXiv : 1304.3147 . Bibcode : 2013PhRvE..88a2127H. doi : 10.1103/physreve.88.012127. PMID  23944434. S2CID  8184675..
17. Сибли, Томас К. (2015). Думать геометрически: обзор геометрий. Математическая ассоциация Америки. стр. 53. ISBN 978-1-939512-08-6.
18. Sloane, NJA ; Hardin, RH; Duff, TDS; Conway, JH (1995), «Кластеры твердых сфер с минимальной энергией», Discrete & Computational Geometry , 14 (3): 237–259, doi : 10.1007/BF02570704 , MR  1344734, S2CID  26955765
19. Шварц, Ричард Эван (2013). «Пятиэлектронный случай проблемы Томсона». Experimental Mathematics . 22 (2): 157–186. doi :10.1080/10586458.2013.766570. S2CID  38679186.
20. Петруччи, Р. Х.; Харвуд, В. С.; Херринг, Ф. Г. (2002). Общая химия: принципы и современные приложения (8-е изд.). Prentice-Hall. стр. 413–414. ISBN 978-0-13-014329-7.См. таблицу 11.1.
21. Housecroft, CE; Sharpe, AG (2004). Неорганическая химия (2-е изд.). Prentice Hall. стр. 407. ISBN 978-0-13-039913-7.
22. Кюхни, Рольф Г. (2003). Цветовое пространство и его подразделения: цветовой порядок от античности до наших дней. John & Sons Wiley. стр. 53. ISBN 978-0-471-46146-3.
23. Kuehni, Rolf G. (2013). Цвет: Введение в практику и принципы. John & Sons Wiley. стр. 198. ISBN 978-1-118-17384-8.