stringtranslate.com

Треугольник Пенроуза

Треугольник Пенроуза

Треугольник Пенроуза , также известный как треугольни́ца Пенроуза , невозможный треугольни́ца , [1] или невозможный треугольник , [2] — это треугольный невозможный объект , оптическая иллюзия, состоящая из объекта, который может быть изображён на перспективном рисунке. Он не может существовать как твёрдый объект в обычном трёхмерном евклидовом пространстве, хотя его поверхность может быть изометрически вложена (согнута, но не растянута) в пятимерном евклидовом пространстве. [3] Впервые он был создан шведским художником Оскаром Рейтерсвардом в 1934 году. [4] Независимо от Рейтерсварда треугольник был придуман и популяризирован в 1950-х годах психиатром Лайонелом Пенроузом и его сыном, математиком и лауреатом Нобелевской премии Роджером Пенроузом , который описал его как «невозможность в своей чистейшей форме». [5] Он занимает видное место в работах художника М. К. Эшера , чьи ранние изображения невозможных объектов отчасти вдохновили его.

Описание

Вращающаяся модель треугольника Пенроуза для демонстрации иллюзии. В момент иллюзии кажется, что есть пара фиолетовых граней (одна частично закрытая), соединенных под прямым углом, но на самом деле это параллельные грани, а частично закрытая грань является внутренней, а не внешней.

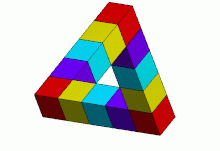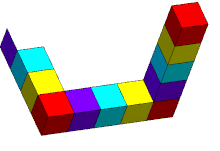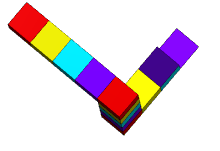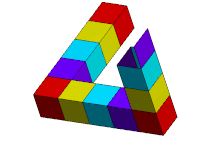
Трибар/треугольник выглядит как сплошной объект, состоящий из трех прямых балок квадратного сечения, которые попарно встречаются под прямым углом в вершинах треугольника, который они образуют. Балки могут быть сломаны, образуя кубы или прямоугольные параллелепипеды.

Эта комбинация свойств не может быть реализована никаким трехмерным объектом в обычном евклидовом пространстве . Такой объект может существовать в определенных евклидовых 3-многообразиях . [6] Поверхность с теми же геодезическими расстояниями , что и изображенная поверхность трибара, но без ее плоской формы и прямых углов, которые должны быть сохранены, может также существовать в 5-мерном евклидовом пространстве, которое является евклидовым пространством наименьшей размерности, в которое эта поверхность может быть изометрически вложена. [3] Существуют также трехмерные твердые формы, каждая из которых при просмотре под определенным углом выглядит так же, как 2-мерное изображение треугольника Пенроуза на этой странице (например, соседнее изображение, изображающее скульптуру в Перте , Австралия ). Термин «Треугольник Пенроуза» может относиться к 2-мерному изображению или самому невозможному объекту.

Если провести линию вокруг треугольника Пенроуза, получится лента Мёбиуса с четырьмя петлями. [7]

Изображения

Иллюзия треугольника Рейтерсварда, напечатанная на 3D-принтере

Литография М. К. Эшера « Водопад » (1961) изображает водный поток, который течет зигзагом вдоль длинных сторон двух удлиненных треугольников Пенроуза, так что он заканчивается на два этажа выше, чем начинался. Получившийся водопад, образующий короткие стороны обоих треугольников, приводит в движение водяное колесо . Эшер указывает, что для того, чтобы колесо продолжало вращаться, необходимо время от времени добавлять немного воды, чтобы компенсировать испарение . Третий треугольник Пенроуза лежит между двумя другими, образованный двумя сегментами водного пути и опорной башней. [8]

Скульптуры

Смотрите также

Ссылки

  1. ^ Паппас, Теони (1989). «Невозможный трибар». Радость математики: открытие математики вокруг вас . Сан-Карлос, Калифорния: Wide World Publ./Tetra. стр. 13.
  2. ^ Брауэр, Джеймс Р.; Рубин, Дэвид К. (июнь 1979). «Простая конструкция невозможного треугольника». Perception . 8 (3): 349–350. doi :10.1068/p080349. PMID  534162. S2CID  41895719.
  3. ^ ab Zeng, Zhenbing; Xu, Yaochen; Yang, Zhengfeng; Li, Zhi-bin (2021). «Изометрическое вложение невозможного треугольника в евклидово пространство наименьшей размерности» (PDF) . В Corless, Robert M.; Gerhard, Jürgen; Kotsireas, Ilias S. (ред.). Maple в математическом образовании и исследованиях: 4-я конференция Maple, MC 2020, Ватерлоо, Онтарио, Канада, 2–6 ноября 2020 г., пересмотренные избранные статьи . Springer International Publishing. стр. 438–457. doi :10.1007/978-3-030-81698-8_29. ISBN 9783030816988.
  4. ^ Эрнст, Бруно (1986). «Невозможные фигуры Эшера печатаются в новом контексте». В Coxeter, HSM ; Emmer, M.; Penrose, R .; Teuber, ML (ред.). Искусство и наука М. К. Эшера: Труды Международного конгресса по М. К. Эшеру, Рим, Италия, 26–28 марта 1985 г. Северная Голландия. стр. 125–134.См. в частности стр. 131.
  5. ^ Пенроуз, Л. С .; Пенроуз, Р. (февраль 1958 г.). «Невозможные объекты: особый тип зрительной иллюзии». British Journal of Psychology . 49 (1): 31–33. doi :10.1111/j.2044-8295.1958.tb00634.x. PMID  13536303.
  6. ^ Фрэнсис, Джордж К. (1988). "Глава 4: Невозможный трибар". Топологическая иллюстрированная книга . Springer. стр. 65–76. doi :10.1007/978-0-387-68120-7_4. ISBN 0-387-96426-6.См., в частности, стр. 68, где Фрэнсис приписывает это наблюдение Джону Стиллвеллу .
  7. ↑ Гарднер, Мартин (август 1978 г.). «Математические игры: лента Мёбиуса имеет конечную толщину, поэтому она на самом деле является скрученной призмой». Scientific American . 239 (2): 18–26. doi :10.1038/scientificamerican1278-18. JSTOR  24960346.
  8. ^ MC Эшер: Графическая работа . Ташен. 2000. с. 16. ISBN 9783822858646.
  9. ^ Федоров, Ю. (1972). «Невозможное-Возможно». Техника Молодежи . 4 : 20–21.

Внешние ссылки