
В геометрии ориентация , отношение , направление , направление или угловое положение объекта — например, линии , плоскости или твердого тела — являются частью описания того, как он размещен в пространстве, которое он занимает. [1] Более конкретно, это относится к воображаемому вращению , которое необходимо для перемещения объекта из исходного положения в его текущее положение. Вращение может быть недостаточным для достижения текущего положения, в этом случае может потребоваться добавить воображаемое перемещение , чтобы изменить положение объекта (или линейное положение). Положение и ориентация вместе полностью описывают, как объект размещен в пространстве. Вышеупомянутые воображаемое вращение и перемещение можно рассматривать как происходящие в любом порядке, поскольку ориентация объекта не меняется при его перемещении, а его положение не меняется при вращении.
Теорема вращения Эйлера показывает, что в трех измерениях любая ориентация может быть достигнута одним вращением вокруг фиксированной оси . Это дает один общий способ представления ориентации с использованием представления ось-угол . Другие широко используемые методы включают кватернионы вращения , роторы , углы Эйлера или матрицы вращения . Более специализированные применения включают индексы Миллера в кристаллографии, простирание и падение в геологии и сорт на картах и знаках. Единичный вектор также может использоваться для представления направления нормального вектора объекта или относительного направления между двумя точками.
Обычно ориентация задается относительно системы отсчета , обычно заданной декартовой системой координат .
В общем случае положение и ориентация в пространстве твердого тела определяются как положение и ориентация относительно основной системы отсчета другой системы отсчета, которая фиксирована относительно тела и, следовательно, перемещается и вращается вместе с ним ( локальная система отсчета тела или локальная система координат ). Для описания ориентации этой локальной системы отсчета необходимы как минимум три независимых значения. Три других значения описывают положение точки на объекте. Все точки тела изменяют свое положение во время вращения, за исключением тех, которые лежат на оси вращения. Если твердое тело имеет вращательную симметрию , не все ориентации различимы, за исключением наблюдения за тем, как ориентация меняется со временем от известной начальной ориентации. Например, ориентация в пространстве линии , отрезка линии или вектора может быть задана только двумя значениями, например, двумя направляющими косинусами . Другим примером является положение точки на Земле, часто описываемое с помощью ориентации линии, соединяющей ее с центром Земли, измеренной с использованием двух углов долготы и широты . Аналогично, ориентация плоскости может быть описана двумя значениями, например, путем указания ориентации линии, перпендикулярной этой плоскости, или с использованием углов простирания и падения.
Более подробная информация о математических методах представления ориентации твердых тел и плоскостей в трех измерениях приведена в следующих разделах.
В двух измерениях ориентация любого объекта (линии, вектора или плоской фигуры ) задается одним значением: углом, на который он повернулся. Существует только одна степень свободы и только одна фиксированная точка, вокруг которой происходит вращение.
При наличии d измерений для указания ориентации объекта, не имеющего вращательной симметрии, требуется d ( d − 1) / 2 независимых значений.
Разработано несколько методов описания ориентаций твердого тела в трех измерениях. Они обобщены в следующих разделах.

Первая попытка представить ориентацию приписывается Леонарду Эйлеру . Он представил себе три системы отсчета, которые могли вращаться одна вокруг другой, и понял, что, начав с фиксированной системы отсчета и выполнив три поворота, он может получить любую другую систему отсчета в пространстве (используя два поворота для фиксации вертикальной оси и еще один для фиксации двух других осей). Значения этих трех поворотов называются углами Эйлера .

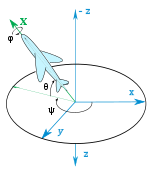
Это три угла, также известные как рыскание, тангаж и крен, навигационные углы и карданные углы. Математически они составляют набор из шести возможностей внутри двенадцати возможных наборов углов Эйлера, причем порядок является наилучшим для описания ориентации транспортного средства, такого как самолет. В аэрокосмической технике их обычно называют углами Эйлера.

Эйлер также понял, что композиция двух вращений эквивалентна одному вращению вокруг другой фиксированной оси ( теорема вращения Эйлера ). Поэтому композиция первых трех углов должна быть равна только одному вращению, ось которого было сложно вычислить, пока не были разработаны матрицы.
На основании этого факта он ввел векторный способ описания любого вращения с вектором на оси вращения и модулем, равным значению угла. Таким образом, любая ориентация может быть представлена вектором вращения (также называемым вектором Эйлера), который приводит к ней из системы отсчета. При использовании для представления ориентации вектор вращения обычно называется вектором ориентации или вектором отношения.
Похожий метод, называемый представлением оси и угла , описывает вращение или ориентацию с помощью единичного вектора, совмещенного с осью вращения, и отдельного значения для указания угла (см. рисунок).
С введением матриц теоремы Эйлера были переписаны. Вращения описывались ортогональными матрицами, называемыми матрицами вращения или матрицами направляющих косинусов. При использовании для представления ориентации матрица вращения обычно называется матрицей ориентации или матрицей отношения.
Вышеупомянутый вектор Эйлера является собственным вектором матрицы вращения (матрица вращения имеет единственное действительное собственное значение ). Произведение двух матриц вращения является композицией вращений. Поэтому, как и прежде, ориентация может быть задана как вращение от исходной системы отсчета для достижения системы отсчета, которую мы хотим описать.
Конфигурационное пространство несимметричного объекта в n -мерном пространстве равно SO( n ) × R n . Ориентацию можно визуализировать, прикрепив к объекту базис касательных векторов . Направление, в котором указывает каждый вектор , определяет его ориентацию.
Другой способ описания вращений — использование кватернионов вращения , также называемых версорами. Они эквивалентны матрицам вращения и векторам вращения. Что касается векторов вращения, их можно легче преобразовать в матрицы и из матриц. При использовании для представления ориентаций кватернионы вращения обычно называются кватернионами ориентации или кватернионами отношения.
Положение твердого тела — это его ориентация, описанная, например, ориентацией рамки, закрепленной в теле, относительно неподвижной системы отсчета. Положение описывается координатами положения и состоит как минимум из трех координат. [2] Одна схема ориентации твердого тела основана на вращении осей тела; последовательные вращения три раза вокруг осей неподвижной системы отсчета тела, тем самым устанавливая углы Эйлера тела . [3] [4] Другая основана на крене, тангаже и рыскании , [5] хотя эти термины также относятся к постепенным отклонениям от номинального положения
положение плоскости или линии, то есть ее ориентация в пространстве, имеет основополагающее значение для описания структур.
Угол Эйлера в положении твердого тела.