Универсальная вершина

Vertex adjacent to all others in a graph

Граф с универсальной вершиной u

В теории графов универсальная вершина — это вершина неориентированного графа , которая смежна со всеми остальными вершинами графа. Она также может называться доминирующей вершиной , поскольку образует одноэлементное доминирующее множество в графе. Граф, содержащий универсальную вершину, может называться конусом , а его универсальная вершина может называться вершиной конуса. ^[1] Эту терминологию следует отличать от несвязанного использования этих слов для универсальных кванторов в логике графов и для вершинных графов .

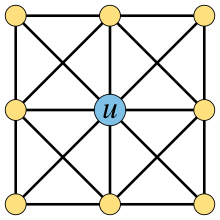
Графы, содержащие универсальную вершину, включают звезды , тривиально совершенные графы и графы дружбы . Для графов-колес (графов пирамид ) и графов многомерных пирамидальных многогранников вершина на вершине пирамиды является универсальной. Когда граф содержит универсальную вершину, он является графом cop-win , и почти все графы cop-win содержат универсальную вершину.

Число помеченных графов, содержащих универсальную вершину, можно подсчитать методом включения-исключения , показывающим, что существует нечетное число таких графов на любом четном числе вершин. Это, в свою очередь, можно использовать для того, чтобы показать, что свойство наличия универсального графа является уклончивым : проверка этого свойства может потребовать проверки смежности всех пар вершин. Однако универсальную вершину можно сразу распознать по ее степени : в графе с -вершинами она имеет степень . Универсальные вершины можно описать короткой логической формулой, которая использовалась в алгоритмах графов для связанных свойств. ${\displaystyle n}$ ${\displaystyle n-1}$

В специальных семействах графов

Четыре типа графа с универсальной вершиной: звезда (вверху слева), граф-колесо (вверху справа), граф дружбы (внизу слева) и граф порога (внизу справа). В каждом примере универсальной вершиной является центральная желтая вершина.

Звезды — это именно те деревья , которые имеют универсальную вершину и могут быть построены путем добавления универсальной вершины к независимому множеству . Колесные графы могут быть образованы путем добавления универсальной вершины к циклическому графу . ^[2] Тривиально совершенные графы получаются из корневых деревьев путем добавления ребра, соединяющего каждую пару предок-потомок в дереве. Они всегда содержат универсальную вершину, корень дерева. Более строго их можно охарактеризовать как конечные графы, в которых каждый связанный индуцированный подграф содержит универсальную вершину. ^[3] Связанные пороговые графы образуют подкласс тривиально совершенных графов, поэтому они также содержат универсальную вершину. Их можно определить как графы, которые могут быть образованы путем повторного добавления либо универсальной вершины, либо изолированной вершины (вершины без инцидентных ребер). ^[4]

В геометрии трехмерные пирамиды имеют графы колес в качестве своих скелетов , ^[5] и в более общем смысле многомерная пирамида - это многогранник, грани всех измерений которого соединяют вершину вершины со всеми гранями основания меньшей размерности, включая все вершины основания. Многогранник называется пирамидальным в своей вершине, и он может иметь более одной вершины. Однако существование соседних многогранников означает, что граф многогранника может иметь универсальную вершину или все вершины универсальны, при этом сам многогранник не является пирамидой. ^[6]

Теорема о дружбе гласит, что если каждые две вершины в конечном графе имеют ровно одного общего соседа, то граф содержит универсальную вершину. Графы, описываемые этой теоремой, являются графами дружбы , образованными системами треугольников, соединенных вместе в общей общей вершине, универсальной вершине. ^[7] Предположение о том, что граф конечен, важно; существуют бесконечные графы, в которых каждые две вершины имеют одного общего соседа, но не имеют универсальной вершины. ^[8]

Каждый конечный граф с универсальной вершиной является демонтируемым графом , что означает, что его можно свести к одной вершине, многократно удаляя вершину, замкнутое соседство которой является подмножеством замкнутого соседства другой вершины. В графе с универсальной вершиной любая последовательность удаления, которая оставляет универсальную вершину на месте, удаляя все остальные вершины, соответствует этому определению. Почти все демонтируемые графы имеют универсальную вершину, в том смысле, что доля -вершинных демонтируемых графов, которые имеют универсальную вершину, стремится к единице в пределе, стремящемся к бесконечности. Демонтируемые графы также называются графами полицейской победы, потому что сторона, играющая полицейскую, выигрывает определенную игру полицейского и грабителя, определенную на этих графах. ^[9] ${\displaystyle n}$ ${\displaystyle n}$

Когда граф имеет универсальную вершину, множество вершин, состоящее только из этой вершины, является доминирующим множеством , множеством, которое включает или смежно с каждой вершиной. По этой причине в контексте задач доминирующего множества универсальная вершина может также называться доминирующей вершиной . ^[10] Для сильного произведения графов доминирующие числа и подчиняются неравенствам Это означает, что сильное произведение имеет доминирующую вершину тогда и только тогда, когда оба его фактора подчиняются; в этом случае верхняя граница его доминирующего числа равна единице, а в любом другом случае нижняя граница больше единицы. ^[11] ${\displaystyle G\boxtimes H}$ ${\displaystyle \gamma (G)}$ ${\displaystyle \gamma (H)}$ $${\displaystyle \max\{\gamma (G),\gamma (H)\}\leq \gamma (G\boxtimes H)\leq \gamma (G)\gamma (H).}$$

Комбинаторное перечисление

Число помеченных графов с вершинами, по крайней мере одна из которых является универсальной (или, что эквивалентно, изолированной в дополнительном графе ), можно подсчитать с помощью принципа включения-исключения , в котором подсчитываются графы, в которых одна выбранная вершина является универсальной, затем вносится поправка на пересчет путем вычитания количества для графов с двумя выбранными универсальными вершинами, затем сложения количества для графов с тремя выбранными универсальными вершинами и т. д. Это дает формулу ${\displaystyle n}$

${\displaystyle \displaystyle \sum _{k=1}^{n}(-1)^{k+1}{\binom {n}{k}}2^{\tbinom {n-k}{2}}.}$

В каждом члене суммы — число вершин, выбранных в качестве универсальных, а — число способов сделать этот выбор. — число пар вершин, которые не включают выбранную универсальную вершину, и, взяв это число в качестве показателя степени двойки, подсчитываем число графов с выбранными вершинами в качестве универсальных. ^[12] ${\displaystyle k}$ ${\displaystyle {\tbinom {n}{k}}}$ ${\displaystyle {\tbinom {n-k}{2}}}$

Начиная с , эти номера графиков следующие: ${\displaystyle n=1}$

1, 1, 4, 23, 256, 5319, 209868, 15912975, 2343052576, 675360194287, ... (последовательность A327367 в OEIS ). ^[13]

Для эти числа нечетны, когда четны, и наоборот. ^[12] Немаркированная версия этой задачи перечисления графов тривиальна в том смысле, что количество -вершинных немаркированных графов с универсальной вершиной совпадает с количеством -вершинных графов. ^[13] ${\displaystyle n>1}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle (n-1)}$

Признание

В графе с вершинами универсальная вершина — это вершина, степень которой равна точно . ^[10] ${\displaystyle n}$ ${\displaystyle n-1}$

Свойство иметь универсальную вершину может быть выражено формулой в логике первого порядка графов . Используя для указания отношения смежности в графе, граф имеет универсальную вершину тогда и только тогда, когда он моделирует формулу Существование этой формулы и ее небольшое количество чередований между универсальными и экзистенциальными кванторами может быть использовано в фиксированно-параметрическом легко поддающемся обработке алгоритме для проверки того, можно ли сделать так, чтобы все компоненты графа имели универсальные вершины путем удаления вершины из каждого компонента. ^[14] ${\displaystyle \sim }$ ${\displaystyle G}$ $${\displaystyle \exists u\forall v{\bigl (}(u\neq v)\Rightarrow (u\sim v){\bigr )}.}$$ ${\displaystyle k}$

Свойство наличия универсальной вершины (или, что эквивалентно, изолированной вершины) рассматривалось в отношении гипотезы Аандерраа–Карпа–Розенберга о том, сколько запросов (вызовов подпрограмм) необходимо для проверки того, имеет ли помеченный граф свойство, при условии доступа к графу только через подпрограмму, которая может проверить, являются ли две заданные вершины смежными. В графе с вершинами можно определить весь граф и проверить любое свойство, используя запросы. Свойство графа является уклончивым , если ни один алгоритм не может проверить свойство, гарантируя меньшее количество запросов. Проверка существования универсальной вершины является уклончивой на графах с четным числом вершин. Существует нечетное число таких графов, имеющих универсальную вершину. Алгоритм тестирования может быть вынужден опрашивать все пары вершин с помощью подпрограммы смежности, которая всегда отвечает таким образом, чтобы оставить нечетное число оставшихся графов, имеющих универсальную вершину. Пока все ребра не будут проверены, общее число оставшихся графов будет четным, поэтому алгоритм не сможет определить, имеет ли запрашиваемый им граф универсальную вершину. ^[12] ${\displaystyle n}$ ${\displaystyle {\tbinom {n}{2}}}$

Ссылки

1. Larrión, F.; de Mello, CP; Morgana, A.; Neumann-Lara, V .; Pizaña, MA (2004), «Оператор клики на кографах и последовательных графах», Discrete Mathematics , 282 (1–3): 183–191, doi :10.1016/j.disc.2003.10.023, MR  2059518.
2. Бонато, Энтони (2008), Курс по веб-графу, Graduate Studies in Mathematics, т. 89, Атлантическая ассоциация исследований в области математических наук (AARMS), Галифакс, Новая Шотландия, стр. 7, doi : 10.1090/gsm/089, ISBN 978-0-8218-4467-0, МР  2389013.
3. Wolk, ES (1962), «Граф сравнимости дерева», Труды Американского математического общества , 13 (5): 789–795, doi : 10.2307/2034179 , JSTOR  2034179, MR  0172273.
4. Chvátal, Václav ; Hammer, Peter Ladislaw (1977), "Aggregation of inequalitys in integer programming", in Hammer, PL; Johnson, EL; Korte, BH; Nemhauser, GL (eds.), Studies in Integer Programming (Proc. Worksh. Bonn 1975) , Annals of Discrete Mathematics, т. 1, Амстердам: North-Holland, стр. 145–162.
5. Писански, Томаж ; Серватиус, Бригитта (2013), Конфигурация с графической точки зрения, Springer, стр. 21, doi :10.1007/978-0-8176-8364-1, ISBN 978-0-8176-8363-4
6. Клее, Виктор (1964), «О числе вершин выпуклого многогранника», Канадский математический журнал , 16 : 701–720, doi :10.4153/CJM-1964-067-6, MR  0166682
7. Эрдеш, Пол ; Реньи, Альфред ; Сос, Вера Т. (1966), «Об одной задаче теории графов» (PDF) , Studia Sci. Математика. Венгрия. , 1 : 215–235.
8. Chvátal, Václav ; Kotzig, Anton ; Rosenberg, Ivo G.; Davies, Roy O. (1976), «Существуют графы дружбы кардинального числа », Canadian Mathematical Bulletin , 19 (4): 431–433, doi : 10.4153/cmb-1976-064-1 ${\displaystyle \scriptstyle 2^{\aleph _{\alpha }}}$ ${\displaystyle \scriptstyle \aleph _{\alpha }}$.
9. Бонато, Энтони; Кемкес, Грэм; Пралат, Павел (2012), «Почти все графы cop-win содержат универсальную вершину», Дискретная математика , 312 (10): 1652–1657, doi : 10.1016/j.disc.2012.02.018 , MR  2901161.
10. Haynes, Teresa W. ; Hedetniemi, Stephen T. ; Henning, Michael A. (2023), Domination in Graphs: Core Concepts , Springer Monographs in Mathematics, Springer, Cham, стр. 2, doi : 10.1007/978-3-031-09496-5, ISBN 978-3-031-09495-8, МР  4607811
11. Фишер, Дэвид К. (1994), «Доминирование, дробное доминирование, 2-упаковка и графовые произведения», SIAM Journal on Discrete Mathematics , 7 (3): 493–498, doi :10.1137/S0895480191217806, MR  1285586
12. Ловас, Ласло ; Янг, Нил Э. (2002), «Конспекты лекций об уклончивости свойств графов», arXiv : cs/0205031
13. Sloane, N. J. A. (ред.), "Последовательность A327367 (Число помеченных простых графов с n вершинами, по крайней мере одна из которых изолирована)", The On-Line Encyclopedia of Integer Sequences , OEIS Foundation
14. Фомин, Федор В .; Головач, Петр А.; Тиликос, Димитриос М. (2021), «Параметризованная сложность расстояния исключения до свойств логики первого порядка», 36-й ежегодный симпозиум ACM/IEEE по логике в компьютерных науках, LICS 2021, Рим, Италия, 29 июня - 2 июля 2021 г. , IEEE, стр. 1–13, arXiv : 2104.02998 , doi : 10.1109/LICS52264.2021.9470540, ISBN 978-1-6654-4895-6, S2CID  233169117