Ферми-газ

Физическая модель газов, состоящих из множества невзаимодействующих идентичных фермионов

Ферми -газ — это идеализированная модель, ансамбль многих невзаимодействующих фермионов . Фермионы — это частицы , подчиняющиеся статистике Ферми–Дирака , как электроны , протоны и нейтроны , и, в общем случае, частицы с полуцелым спином . Эта статистика определяет распределение энергии фермионов в ферми-газе в тепловом равновесии и характеризуется их плотностью числа , температурой и набором доступных энергетических состояний. Модель названа в честь итальянского физика Энрико Ферми . ^{[1] [2]}

Эта физическая модель полезна для определенных систем со многими фермионами. Некоторые ключевые примеры — поведение носителей заряда в металле , нуклонов в атомном ядре , нейтронов в нейтронной звезде и электронов в белом карлике .

Описание

Идеальный ферми-газ или свободный ферми-газ — это физическая модель , предполагающая совокупность невзаимодействующих фермионов в постоянной потенциальной яме . Фермионы — это элементарные или составные частицы с полуцелым спином, поэтому следуют статистике Ферми–Дирака . Эквивалентная модель для частиц с целым спином называется бозе-газом (ансамблем невзаимодействующих бозонов ). При достаточно низкой плотности числа частиц и высокой температуре как ферми-газ, так и бозе-газ ведут себя как классический идеальный газ . ^[3]

Согласно принципу исключения Паули , ни одно квантовое состояние не может быть занято более чем одним фермионом с идентичным набором квантовых чисел . Таким образом, невзаимодействующий ферми-газ, в отличие от бозе-газа, концентрирует небольшое количество частиц на единицу энергии. Таким образом, ферми-газу запрещено конденсироваться в конденсат Бозе-Эйнштейна , хотя слабовзаимодействующие ферми-газы могут образовывать куперовскую пару и конденсат (также известный как режим кроссовера БКШ -БЭК). ^[4] Полная энергия ферми-газа при абсолютном нуле больше суммы основных состояний одной частицы , поскольку принцип Паули подразумевает своего рода взаимодействие или давление, которое удерживает фермионы разделенными и движущимися. По этой причине давление ферми -газа не равно нулю даже при нулевой температуре, в отличие от давления классического идеального газа. Например, это так называемое давление вырождения стабилизирует нейтронную звезду (ферми-газ нейтронов) или белую карликовую звезду (ферми-газ электронов) против внутреннего притяжения гравитации , которое якобы сколлапсировало бы звезду в черную дыру . Только когда звезда достаточно массивна, чтобы преодолеть давление вырождения, она может сколлапсировать в сингулярность.

Можно определить температуру Ферми, ниже которой газ можно считать вырожденным (его давление выводится почти исключительно из принципа Паули). Эта температура зависит от массы фермионов и плотности энергетических состояний .

Основное предположение модели свободных электронов для описания делокализованных электронов в металле может быть получено из газа Ферми. Поскольку взаимодействия пренебрегаются из-за эффекта экранирования , проблема рассмотрения равновесных свойств и динамики идеального газа Ферми сводится к изучению поведения отдельных независимых частиц. В этих системах температура Ферми обычно составляет много тысяч кельвинов , поэтому в человеческих приложениях электронный газ можно считать вырожденным. Максимальная энергия фермионов при нулевой температуре называется энергией Ферми . Поверхность энергии Ферми в обратном пространстве известна как поверхность Ферми .

Модель почти свободных электронов адаптирует модель газа Ферми для рассмотрения кристаллической структуры металлов и полупроводников , где электроны в кристаллической решетке заменяются электронами Блоха с соответствующим импульсом кристалла . Таким образом, периодические системы все еще относительно поддаются изучению, и модель формирует отправную точку для более продвинутых теорий, которые имеют дело с взаимодействиями, например, с использованием теории возмущений .

1D однородный газ

Одномерный бесконечный квадратный колодец длины L является моделью одномерного ящика с потенциальной энергией: $${\displaystyle V(x)={\begin{cases}0,&x_{c}-{\tfrac {L}{2}}<x<x_{c}+{\tfrac {L}{2}},\\\infty ,&{\text{otherwise.}}\end{cases}}}$$

Это стандартная модель-система в квантовой механике, для которой решение для одной частицы хорошо известно. Поскольку потенциал внутри ящика однороден, эта модель называется одномерным однородным газом ^[5] , хотя фактический профиль плотности числа газа может иметь узлы и пучности, когда общее число частиц мало.

Уровни обозначены одним квантовым числом n , а энергии определяются следующим образом:

$${\displaystyle E_{n}=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}.}$$где — энергия нулевой точки (которая может быть выбрана произвольно как форма фиксации калибровки ), — масса отдельного фермиона, а — приведенная постоянная Планка . ${\displaystyle E_{0}}$ ${\displaystyle m}$ ${\displaystyle \hbar }$

Для N фермионов со спином - 1 ⁄ 2 в ящике не более двух частиц могут иметь одинаковую энергию, т. е. две частицы могут иметь энергию , две другие частицы могут иметь энергию и т. д. Две частицы с одинаковой энергией имеют спин 1 ⁄ 2 (спин вверх) или − 1 ⁄ 2 (спин вниз), что приводит к двум состояниям для каждого уровня энергии. В конфигурации, для которой полная энергия самая низкая (основное состояние), все уровни энергии до n  =  N / 2 заняты, а все более высокие уровни пусты. ${\textstyle E_{1}}$ ${\textstyle E_{2}}$

Если определить точку отсчета для энергии Ферми как , то энергия Ферми, таким образом, определяется выражением , где — функция пола, вычисленная при n  =  N /2. ${\displaystyle E_{0}}$ $${\displaystyle E_{\mathrm {F} }^{({\text{1D}})}=E_{n}-E_{0}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(\left\lfloor {\frac {N}{2}}\right\rfloor \right)^{2},}$$ ${\textstyle \left\lfloor {\frac {N}{2}}\right\rfloor }$

Термодинамический предел

В термодинамическом пределе общее число частиц N настолько велико, что квантовое число n можно рассматривать как непрерывную переменную. В этом случае общий профиль плотности числа в ящике действительно однороден.

Число квантовых состояний в диапазоне равно: ${\displaystyle n_{1}<n<n_{1}+dn}$ $${\displaystyle D_{n}(n_{1})\,dn=2\,dn\,.}$$

Без потери общности , нулевая энергия выбрана равной нулю, что дает следующий результат:

$${\displaystyle E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\implies dE={\frac {\hbar ^{2}\pi ^{2}}{mL^{2}}}n\,dn={\frac {\hbar \pi }{L}}{\sqrt {\frac {2E}{m}}}dn\,.}$$

Следовательно, в диапазоне: число квантовых состояний равно: $${\displaystyle E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{1}^{2}<E<E_{1}+dE\,,}$$ $${\displaystyle D_{n}(n_{1})\,dn=2{\frac {dE}{dE/dn}}={\frac {2}{{\frac {\hbar ^{2}\pi ^{2}}{mL^{2}}}n}}\,dE\equiv D(E_{1})\,dE\,.}$$

Здесь степень вырождения равна:

$${\displaystyle D(E)={\frac {2}{dE/dn}}={\frac {2L}{\hbar \pi }}{\sqrt {\frac {m}{2E}}}\,.}$$

А плотность состояний равна:

$${\displaystyle g(E)\equiv {\frac {1}{L}}D(E)={\frac {2}{\hbar \pi }}{\sqrt {\frac {m}{2E}}}\,.}$$

В современной литературе ^[5] указанное выше иногда также называют «плотностью состояний». Однако, отличается от на множитель объема системы (который в данном случае является одномерным). ${\displaystyle D(E)}$ ${\displaystyle g(E)}$ ${\displaystyle D(E)}$ ${\displaystyle L}$

На основе следующей формулы:

$${\displaystyle \int _{0}^{E_{\mathrm {F} }}D(E)\,dE=N\,,}$$

Энергию Ферми в термодинамическом пределе можно рассчитать следующим образом:

$${\displaystyle E_{\mathrm {F} }^{({\text{1D}})}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {N}{2}}\right)^{2}\,.}$$

3D однородный газ

Модель атомного ядра, показывающая его как компактный пучок двух типов нуклонов : протонов (красный) и нейтронов (синий). В первом приближении ядро ​​можно рассматривать как состоящее из невзаимодействующих протонных и нейтронных газов.

Трехмерный изотропный и нерелятивистский однородный случай ферми-газа известен как сфера Ферми .

Трехмерный бесконечный квадратный колодец (т.е. кубический ящик со стороной длиной L ) имеет потенциальную энергию $${\displaystyle V(x,y,z)={\begin{cases}0,&-{\frac {L}{2}}<x,y,z<{\frac {L}{2}},\\\infty ,&{\text{otherwise.}}\end{cases}}}$$

Состояния теперь обозначены тремя квантовыми числами n _x , n _y и n _z . Энергии отдельных частиц равны , где n _x , n _y , n _z являются положительными целыми числами. В этом случае несколько состояний имеют одинаковую энергию (известную как вырожденные уровни энергии ), например . $${\displaystyle E_{n_{x},n_{y},n_{z}}=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,,}$$ ${\displaystyle E_{211}=E_{121}=E_{112}}$

Термодинамический предел

Когда ящик содержит N невзаимодействующих фермионов спина- ⁠1/2⁠ , интересно вычислить энергию в термодинамическом пределе, где N настолько велико, что квантовые числа n _x , n _y , n _z можно рассматривать как непрерывные переменные.

При использовании вектора каждое квантовое состояние соответствует точке в «n-пространстве» с энергией ${\displaystyle \mathbf {n} =(n_{x},n_{y},n_{z})}$ $${\displaystyle E_{\mathbf {n} }=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|\mathbf {n} |^{2}\,}$$

С обозначением квадрата обычной евклидовой длины . Число состояний с энергией, меньшей E _F  + E ₀ , равно числу состояний, которые лежат внутри сферы радиуса в области n-пространства, где n _x , n _y , n _z положительны. В основном состоянии это число равно числу фермионов в системе: ${\displaystyle |\mathbf {n} |^{2}}$ ${\displaystyle |\mathbf {n} |={\sqrt {n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}}$ ${\displaystyle |\mathbf {n} _{\mathrm {F} }|}$

$${\displaystyle N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{\mathrm {F} }^{3}}$$

Свободные фермионы, занимающие самые низкие энергетические состояния, образуют сферу в обратном пространстве . Поверхность этой сферы — поверхность Ферми .

Фактор два выражает два спиновых состояния, а фактор 1/8 выражает долю сферы, которая лежит в области, где все n положительны. Энергия Ферми определяется как $${\displaystyle n_{\mathrm {F} }=\left({\frac {3N}{\pi }}\right)^{1/3}}$$ $${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{\mathrm {F} }^{2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}}$$

Что приводит к соотношению между энергией Ферми и числом частиц в объеме (когда L ² заменяется на V ^2/3 ):

${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}}$

Это также энергия частицы с самой высокой энергией ( й частицы), выше энергии нулевой точки . й частицы имеет энергию ${\displaystyle N}$ ${\displaystyle E_{0}}$ ${\displaystyle N'}$ $${\displaystyle E_{N'}=E_{0}+{\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N'}{V}}\right)^{2/3}\,=E_{0}+E_{\mathrm {F} }{\big |}_{N'}}$$

Полная энергия ферми-сферы фермионов (которые занимают все энергетические состояния внутри ферми-сферы) определяется по формуле: ${\displaystyle N}$ ${\displaystyle N}$

$${\displaystyle E_{\rm {T}}=NE_{0}+\int _{0}^{N}E_{\mathrm {F} }{\big |}_{N'}\,dN'=\left({\frac {3}{5}}E_{\mathrm {F} }+E_{0}\right)N}$$

Таким образом, средняя энергия на частицу определяется по формуле: $${\displaystyle E_{\mathrm {av} }=E_{0}+{\frac {3}{5}}E_{\mathrm {F} }}$$

Плотность состояний

Плотность состояний (DOS) ферми-газа в 3-х измерениях

Для трехмерного однородного ферми-газа с фермионами спина- ⁠1/2⁠ число частиц как функция энергии получается путем замены энергии Ферми на переменную энергию : ${\textstyle N(E)}$ ${\textstyle (E-E_{0})}$

$${\displaystyle N(E)={\frac {V}{3\pi ^{2}}}\left[{\frac {2m}{\hbar ^{2}}}(E-E_{0})\right]^{3/2},}$$

из которого можно получить плотность состояний (число энергетических состояний на энергию на объем) . Ее можно рассчитать, дифференцируя число частиц по энергии: ${\displaystyle g(E)}$

$${\displaystyle g(E)={\frac {1}{V}}{\frac {\partial N(E)}{\partial E}}={\frac {1}{2\pi ^{2}}}\left({\frac {2m}{\hbar ^{2}}}\right)^{3/2}{\sqrt {E-E_{0}}}.}$$

Этот результат дает альтернативный способ расчета полной энергии сферы Ферми фермионов (которые занимают все энергетические состояния внутри сферы Ферми): ${\displaystyle N}$ ${\displaystyle N}$

$${\displaystyle {\begin{aligned}E_{T}&=\int _{0}^{N}E\mathrm {d} N(E)=EN(E){\big |}_{0}^{N}-\int _{E_{0}}^{E_{0}+E_{F}}N(E)\mathrm {d} E\\&=(E_{0}+E_{F})N-\int _{0}^{E_{F}}N(E)\mathrm {d} (E-E_{0})\\&=(E_{0}+E_{F})N-{\frac {2}{5}}E_{F}N(E_{F})=\left(E_{0}+{\frac {3}{5}}E_{\mathrm {F} }\right)N\end{aligned}}}$$

Термодинамические величины

Давление вырождения

Кривые давления и температуры классических и квантовых идеальных газов (ферми-газ, бозе-газ ) в трех измерениях. Отталкивание Паули в фермионах (таких как электроны) дает им дополнительное давление по сравнению с эквивалентным классическим газом, что наиболее существенно при низкой температуре.

Используя первый закон термодинамики , эта внутренняя энергия может быть выражена как давление, то есть , когда это выражение остается справедливым для температур, намного меньших температуры Ферми. Это давление известно как давление вырождения . В этом смысле системы, состоящие из фермионов, также называются вырожденной материей . $${\displaystyle P=-{\frac {\partial E_{\rm {T}}}{\partial V}}={\frac {2}{5}}{\frac {N}{V}}E_{\mathrm {F} }={\frac {(3\pi ^{2})^{2/3}\hbar ^{2}}{5m}}\left({\frac {N}{V}}\right)^{5/3},}$$

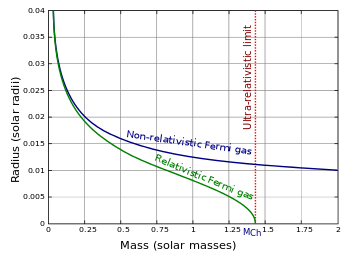
Стандартные звезды избегают коллапса, уравновешивая тепловое давление ( плазма и излучение) против гравитационных сил. В конце жизни звезды, когда тепловые процессы слабеют, некоторые звезды могут стать белыми карликами, которые поддерживаются против гравитации только давлением вырождения электронов . Используя газ Ферми в качестве модели, можно вычислить предел Чандрасекара , т. е. максимальную массу, которую может приобрести любая звезда (без значительного термически генерируемого давления) перед коллапсом в черную дыру или нейтронную звезду. Последняя представляет собой звезду, в основном состоящую из нейтронов, где коллапса также избегает давление вырождения нейтронов.

В случае металлов давление вырождения электронов влияет на сжимаемость или объемный модуль упругости материала.

Химический потенциал

Если предположить, что концентрация фермионов не меняется с температурой, то полный химический потенциал μ (уровень Ферми) трехмерного идеального ферми-газа связан с энергией Ферми при нулевой температуре E _F разложением Зоммерфельда (предполагая ): где T — температура . ^{[6] [7]} ${\displaystyle k_{\rm {B}}T\ll E_{\mathrm {F} }}$ $${\displaystyle \mu (T)=E_{0}+E_{\mathrm {F} }\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {k_{\rm {B}}T}{E_{\mathrm {F} }}}\right)^{2}-{\frac {\pi ^{4}}{80}}\left({\frac {k_{\rm {B}}T}{E_{\mathrm {F} }}}\right)^{4}+\cdots \right],}$$

Следовательно, внутренний химический потенциал , μ - E ₀ , приблизительно равен энергии Ферми при температурах, которые намного ниже характеристической температуры Ферми T _F . Эта характерная температура составляет порядка 10 ⁵ К для металла, поэтому при комнатной температуре (300 К) энергия Ферми и внутренний химический потенциал по существу эквивалентны.

Типичные значения

Металлы

В модели свободных электронов электроны в металле можно рассматривать как однородный ферми-газ. Плотность электронов проводимости в металлах колеблется приблизительно от 10 ²⁸ до 10 ²⁹ электронов на м ³ , что также является типичной плотностью атомов в обычном твердом веществе. Эта плотность дает энергию Ферми порядка: где m _e — масса покоя электрона . ^[8] Эта энергия Ферми соответствует температуре Ферми порядка 10 ⁶ кельвинов, что намного выше температуры поверхности Солнца . Любой металл закипит до достижения этой температуры при атмосферном давлении. Таким образом, для любой практической цели металл можно рассматривать как ферми-газ при нулевой температуре в первом приближении (нормальные температуры малы по сравнению с T _F ). ${\displaystyle N/V}$ $${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{e}}}\left(3\pi ^{2}\ 10^{28\ \sim \ 29}\ \mathrm {m^{-3}} \right)^{2/3}\approx 2\ \sim \ 10\ \mathrm {eV} ,}$$

Белые карлики

Звезды, известные как белые карлики, имеют массу, сравнимую с Солнцем , но имеют радиус, составляющий около одной сотой его радиуса. Высокая плотность означает, что электроны больше не связаны с отдельными ядрами и вместо этого образуют вырожденный электронный газ. Плотность электронов в белом карлике составляет порядка 10 ³⁶ электронов/м ³ . Это означает, что их энергия Ферми равна:

$${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m^{3}} }}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} =0.3\ \mathrm {MeV} }$$

Ядро

Другой типичный пример — частицы в ядре атома. Радиус ядра примерно равен: где A — число нуклонов . $${\displaystyle R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}}$$

Таким образом, плотность нуклонов в ядре равна:

$${\displaystyle \rho ={\frac {A}{{\frac {4}{3}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m^{-3}} }$$

Эту плотность нужно разделить на два, поскольку энергия Ферми применима только к фермионам одного типа. Наличие нейтронов не влияет на энергию Ферми протонов в ядре, и наоборот.

Энергия Ферми ядра приблизительно равна: где m _p — масса протона. $${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{\rm {p}}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{7}\ \mathrm {eV} =30\ \mathrm {MeV} ,}$$

Радиус ядра допускает отклонения вокруг указанного выше значения, поэтому типичное значение энергии Ферми обычно составляет 38 МэВ .

Произвольно-мерный однородный газ

Плотность состояний

Используя интеграл объема по измерениям, плотность состояний равна: ${\textstyle d}$

$${\displaystyle g^{(d)}(E)=g_{s}\int {\frac {\mathrm {d} ^{d}\mathbf {k} }{(2\pi )^{d}}}\delta \left(E-E_{0}-{\frac {\hbar ^{2}|\mathbf {k} |^{2}}{2m}}\right)=g_{s}\ \left({\frac {m}{2\pi \hbar ^{2}}}\right)^{d/2}{\frac {(E-E_{0})^{d/2-1}}{\Gamma (d/2)}}}$$

Энергия Ферми получается путем поиска плотности числа частиц: $${\displaystyle \rho ={\frac {N}{V}}=\int _{E_{0}}^{E_{0}+E_{\mathrm {F} }^{(d)}}g^{(d)}(E)\,dE}$$

Чтобы получить: где - соответствующий d -мерный объем, - размерность для внутреннего гильбертова пространства. Для случая спина- ⁠ $${\displaystyle E_{\mathrm {F} }^{(d)}={\frac {2\pi \hbar ^{2}}{m}}\left({\tfrac {1}{g_{s}}}\Gamma \left({\tfrac {d}{2}}+1\right){\frac {N}{V}}\right)^{2/d}}$$ ${\textstyle V}$ ${\textstyle g_{s}}$1/2⁠ , каждая энергия дважды вырождена, поэтому в этом случае . ${\textstyle g_{s}=2}$

Частный результат получается для , где плотность состояний становится постоянной величиной (не зависит от энергии): ${\displaystyle d=2}$ $${\displaystyle g^{(2\mathrm {D} )}(E)={\frac {g_{s}}{2}}{\frac {m}{\pi \hbar ^{2}}}.}$$

Ферми-газ в гармонической ловушке

Потенциал гармонической ловушки :

$${\displaystyle V(x,y,z)={\frac {1}{2}}m\omega _{x}^{2}x^{2}+{\frac {1}{2}}m\omega _{y}^{2}y^{2}+{\frac {1}{2}}m\omega _{z}^{2}z^{2}}$$

это модельная система с множеством приложений ^[5] в современной физике. Плотность состояний (или, точнее, степень вырождения) для данного вида спина равна:

$${\displaystyle g(E)={\frac {E^{2}}{2(\hbar \omega _{\text{ho}})^{3}}}\,,}$$

где - частота гармонических колебаний. ${\displaystyle \omega _{\text{ho}}={\sqrt[{3}]{\omega _{x}\omega _{y}\omega _{z}}}}$

Энергия Ферми для данного вида спина равна:

$${\displaystyle E_{\rm {F}}=(6N)^{1/3}\hbar \omega _{\text{ho}}\,.}$$

Соответствующие величины Ферми

В современной литературе часто встречаются несколько полезных величин, связанных с энергией Ферми.

Температура Ферми определяется как , где — постоянная Больцмана . Температуру Ферми можно рассматривать как температуру, при которой тепловые эффекты сопоставимы с квантовыми эффектами, связанными со статистикой Ферми. ^[9] Температура Ферми для металла на пару порядков выше комнатной температуры. Другими величинами, определяемыми в этом контексте, являются импульс Ферми , и скорость Ферми ^[10] , которые представляют собой импульс и групповую скорость , соответственно, фермиона на поверхности Ферми . Импульс Ферми также можно описать как , где — радиус сферы Ферми и называется волновым вектором Ферми . ^[11] ${\textstyle T_{\mathrm {F} }={\frac {E_{\mathrm {F} }}{k_{\rm {B}}}}}$ ${\displaystyle k_{\rm {B}}}$ ${\textstyle p_{\mathrm {F} }={\sqrt {2mE_{\mathrm {F} }}}}$ ${\textstyle v_{\mathrm {F} }={\frac {p_{\mathrm {F} }}{m}}}$ ${\displaystyle p_{\mathrm {F} }=\hbar k_{\mathrm {F} }}$ ${\displaystyle k_{\mathrm {F} }}$

Обратите внимание, что эти величины не являются четко определенными в случаях, когда поверхность Ферми не является сферической.

Обработка при конечной температуре

Большой канонический ансамбль

Большинство приведенных выше расчетов точны при нулевой температуре, но остаются хорошими приближениями для температур ниже температуры Ферми. Для других термодинамических переменных необходимо записать термодинамический потенциал . Для ансамбля идентичных фермионов наилучший способ вывести потенциал — из большого канонического ансамбля с фиксированной температурой, объемом и химическим потенциалом μ . Причина кроется в принципе исключения Паули, поскольку числа заполнения каждого квантового состояния задаются либо 1, либо 0 (либо есть электрон, занимающий состояние, либо нет), поэтому (большая) статистическая сумма может быть записана как ${\displaystyle {\mathcal {Z}}}$

${\displaystyle {\mathcal {Z}}(T,V,\mu )=\sum _{\{q\}}e^{-\beta (E_{q}-\mu N_{q})}=\prod _{q}\sum _{n_{q}=0}^{1}e^{-\beta (\varepsilon _{q}-\mu )n_{q}}=\prod _{q}\left(1+e^{-\beta (\varepsilon _{q}-\mu )}\right),}$

где , индексирует ансамбли всех возможных микросостояний, которые дают ту же полную энергию и число частиц , - энергия единичной частицы состояния (она учитывается дважды, если энергия состояния вырождена) и , ее занятость. Таким образом, большой потенциал записывается как ${\displaystyle \beta ^{-1}=k_{\rm {B}}T}$ ${\displaystyle \{q\}}$ ${\textstyle E_{q}=\sum _{q}\varepsilon _{q}n_{q}}$ ${\textstyle N_{q}=\sum _{q}n_{q}}$ ${\textstyle \varepsilon _{q}}$ ${\textstyle q}$ ${\textstyle n_{q}=0,1}$

${\displaystyle \Omega (T,V,\mu )=-k_{\rm {B}}T\ln \left({\mathcal {Z}}\right)=-k_{\rm {B}}T\sum _{q}\ln \left(1+e^{\beta (\mu -\varepsilon _{q})}\right).}$

Тот же результат может быть получен в каноническом и микроканоническом ансамбле , поскольку результат каждого ансамбля должен давать одно и то же значение в термодинамическом пределе . Большой канонический ансамбль рекомендуется здесь, поскольку он избегает использования комбинаторики и факториалов . ${\textstyle (N/V\rightarrow \infty )}$

Как было показано в предыдущих разделах, в макроскопическом пределе мы можем использовать непрерывное приближение ( приближение Томаса–Ферми ), чтобы преобразовать эту сумму в интеграл: где D ( ε ) — полная плотность состояний. $${\displaystyle \Omega (T,V,\mu )=-k_{\rm {B}}T\int _{-\infty }^{\infty }D(\varepsilon )\ln \left(1+e^{\beta (\mu -\varepsilon )}\right)\,d\varepsilon }$$

Связь с распределением Ферми–Дирака

Грандиозный потенциал связан с числом частиц при конечной температуре следующим образом , где производная берется при фиксированной температуре и объеме, и он также известен как распределение Ферми–Дирака . $${\displaystyle N=-\left({\frac {\partial \Omega }{\partial \mu }}\right)_{T,V}=\int _{-\infty }^{\infty }D(\varepsilon ){\mathcal {f}}\left({\frac {\varepsilon -\mu }{k_{\rm {B}}T}}\right)\,\mathrm {d} \varepsilon }$$ $${\displaystyle {\mathcal {f}}(x)={\frac {1}{e^{x}+1}}}$$

Аналогично, полная внутренняя энергия равна $${\displaystyle U=\Omega -T\left({\frac {\partial \Omega }{\partial T}}\right)_{V,\mu }-\mu \left({\frac {\partial \Omega }{\partial \mu }}\right)_{T,V}=\int _{-\infty }^{\infty }D(\varepsilon ){\mathcal {f}}\!\left({\frac {\varepsilon -\mu }{k_{\rm {B}}T}}\right)\varepsilon \,d\varepsilon .}$$

Точное решение для степенной плотности состояний

Многие интересующие нас системы имеют полную плотность состояний в форме степенного закона: для некоторых значений g ₀ , α , ε ₀ . Результаты предыдущих разделов обобщаются на d измерений, давая степенной закон с: $${\displaystyle D(\varepsilon )=Vg(\varepsilon )={\frac {Vg_{0}}{\Gamma (\alpha )}}(\varepsilon -\varepsilon _{0})^{\alpha -1},\qquad \varepsilon \geq \varepsilon _{0}}$$

• α = d /2 для нерелятивистских частиц в d -мерном ящике,
• α = d для нерелятивистских частиц в d -мерной гармонической потенциальной яме,
• α = d для гиперрелятивистских частиц в d -мерном ящике.

Для такой степенной плотности состояний большой потенциальный интеграл оценивается точно как: ^[12] где — полный интеграл Ферми–Дирака (связанный с полилогарифмом ). Из этого большого потенциала и его производных можно восстановить все интересующие термодинамические величины. $${\displaystyle \Omega (T,V,\mu )=-Vg_{0}(k_{\rm {B}}T)^{\alpha +1}F_{\alpha }\left({\frac {\mu -\varepsilon _{0}}{k_{\rm {B}}T}}\right),}$$ ${\displaystyle F_{\alpha }(x)}$

Расширения модели

Релятивистский Ферми-газ

Соотношения радиус–масса для модели белого карлика, релятивистское соотношение против нерелятивистского. Предел Чандрасекара обозначен как M _Ch .

В статье рассматривается только случай, когда частицы имеют параболическую связь между энергией и импульсом, как в случае нерелятивистской механики. Для частиц с энергией, близкой к их соответствующей массе покоя , применимы уравнения специальной теории относительности . Где энергия одной частицы определяется как: $${\displaystyle E={\sqrt {(pc)^{2}+(mc^{2})^{2}}}.}$$

Для этой системы энергия Ферми определяется выражением: где равенство справедливо только в ультрарелятивистском пределе , и ^[13] $${\displaystyle E_{\mathrm {F} }={\sqrt {(p_{\mathrm {F} }c)^{2}+(mc^{2})^{2}}}-mc^{2}\approx p_{\mathrm {F} }c,}$$ ${\displaystyle \approx }$ $${\displaystyle p_{\mathrm {F} }=\hbar \left({\frac {1}{g_{s}}}6\pi ^{2}{\frac {N}{V}}\right)^{1/3}.}$$

Релятивистская модель ферми-газа также используется для описания массивных белых карликов, близких к пределу Чандрасекара . Для ультрарелятивистского случая давление вырождения пропорционально . ${\displaystyle (N/V)^{4/3}}$

Ферми-жидкость

В 1956 году Лев Ландау разработал теорию ферми-жидкости , в которой он рассмотрел случай ферми-жидкости, т. е. системы с отталкивающими, не обязательно малыми, взаимодействиями между фермионами. Теория показывает, что термодинамические свойства идеального ферми-газа и ферми-жидкости не сильно различаются. Можно показать, что ферми-жидкость эквивалентна ферми-газу, состоящему из коллективных возбуждений или квазичастиц , каждая из которых имеет различную эффективную массу и магнитный момент .

Смотрите также

• Бозе-газ
• Фермионный конденсат
• Газ в коробке
• Желе
• Двумерный электронный газ

Ссылки

1. Ферми, Э. (1 ноября 1926). «Zur Quantelung des Idealen Einatomigen Gases» (PDF) . Zeitschrift für Physik (на немецком языке). 36 (11–12): 902–912. Бибкод : 1926ZPhy...36..902F. дои : 10.1007/BF01400221. ISSN  0044-3328. S2CID  123334672. Архивировано из оригинала (PDF) 6 апреля 2019 г.
2. Zannoni, Alberto (1999). "О квантовании идеального одноатомного газа". arXiv : cond-mat/9912229 . Английский перевод оригинальной работы Энрико Ферми по квантованию идеального одноатомного газа приведен в этой статье
3. Швабль, Франц (2013-03-09). Статистическая механика. Springer Science & Business Media. ISBN 978-3-662-04702-6.
4. Regal, CA; Greiner, M.; Jin, DS (2004-01-28). "Наблюдение резонансной конденсации фермионных атомных пар". Physical Review Letters . 92 (4): 040403. arXiv : cond-mat/0401554 . Bibcode : 2004PhRvL..92d0403R. doi : 10.1103/PhysRevLett.92.040403. PMID  14995356. S2CID  10799388.
5. Giorgini, Stefano; Pitaevskii, Lev P.; Stringari, Sandro (2008-10-02). "Теория ультрахолодных атомарных ферми-газов". Reviews of Modern Physics . 80 (4): 1215–1274. arXiv : 0706.3360 . Bibcode :2008RvMP...80.1215G. doi :10.1103/RevModPhys.80.1215. S2CID  117755089.
6. Келли, Джеймс Дж. (1996). "Статистическая механика идеальных ферми-систем" (PDF) . Автономный университет Мадрида . Архивировано из оригинала (PDF) 2018-04-12 . Получено 2018-03-15 .
7. "Вырожденные идеальные ферми-газы" (PDF) . Архивировано из оригинала (PDF) 2008-09-19 . Получено 2014-04-13 .
8. Nave, Rod. "Энергии Ферми, температуры Ферми и скорости Ферми". HyperPhysics . Получено 21.03.2018 .
9. Торре, Чарльз (2015-04-21). "PHYS 3700: Введение в квантовую статистическую термодинамику" (PDF) . Университет штата Юта . Получено 2018-03-21 .
10. Nave, Rod. "Уровень Ферми и функция Ферми". HyperPhysics . Получено 21.03.2018 .
11. Эшкрофт, Нил В.; Мермин, Н. Дэвид (1976). Физика твердого тела . Холт, Райнхарт и Уинстон . ISBN 978-0-03-083993-1.
12. Blundell (2006). "Глава 30: Квантовые газы и конденсаты". Концепции в тепловой физике . Oxford University Press. ISBN 9780198567707.
13. Грейнер, Вальтер ; Нейз, Людвиг; Штёкер, Хорст (1995). Термодинамика и статистическая механика. Классическая теоретическая физика. Springer, Нью-Йорк, штат Нью-Йорк. С. 341–386. doi :10.1007/978-1-4612-0827-3_14. ISBN 9780387942995.

Дальнейшее чтение

• Нил В. Эшкрофт и Н. Дэвид Мермин , Физика твердого тела (Харкорт: Орландо, 1976).
• Чарльз Киттель , Введение в физику твердого тела , 1-е изд. 1953 - 8-е изд. 2005, ISBN 0-471-41526-X