Формула Бете или формула Бете-Блоха описывает среднюю потерю энергии на пройденное расстояние быстрыми заряженными частицами ( протонами , альфа-частицами , атомарными ионами ), пересекающими вещество (или, альтернативно, тормозную способность материала). [1] Для электронов потеря энергии немного отличается из-за их малой массы (требующей релятивистских поправок) и их неразличимости , и поскольку они терпят гораздо большие потери из-за тормозного излучения , необходимо добавить члены, учитывающие это. Быстрые заряженные частицы, движущиеся через вещество, взаимодействуют с электронами атомов в материале. Взаимодействие возбуждает или ионизирует атомы, что приводит к потере энергии движущейся частицы.
Нерелятивистская версия была найдена Гансом Бете в 1930 году; релятивистская версия (показана ниже) была найдена им в 1932 году. [2] Наиболее вероятная потеря энергии отличается от средней потери энергии и описывается распределением Ландау-Вавилова. [3]
Для частицы со скоростью v , зарядом z (кратным заряду электрона) и энергией E , проходящей расстояние x в мишень с плотностью электронов n и средней энергией возбуждения I (см. ниже), релятивистская версия формулы в единицах СИ имеет вид: [2]
где c — скорость света , ε 0 — диэлектрическая проницаемость вакуума , e и m e — заряд электрона и масса покоя соответственно.
Здесь электронную плотность материала можно рассчитать по формуле
где ρ — плотность материала, Z — его атомный номер , A — его относительная атомная масса , N A — число Авогадро и M u — молярная массовая константа .
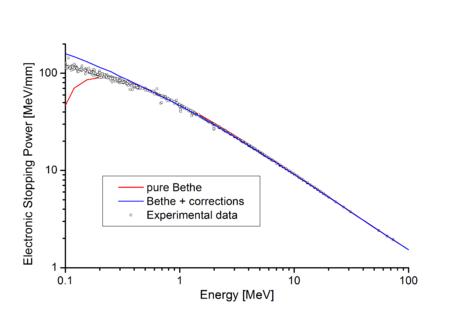
На рисунке справа маленькие кружки — это экспериментальные результаты, полученные из измерений разных авторов, а красная кривая — формула Бете. [4] Очевидно, что теория Бете очень хорошо согласуется с экспериментом при высоких энергиях. Согласие становится еще лучше, если применить поправки (см. ниже).
При малых энергиях, т.е. при малых скоростях частицы β << 1, формула Бете сводится к
Это можно увидеть, сначала заменив βc на v в уравнении (1), а затем пренебрегши β2 из-за его малости.
При низкой энергии потеря энергии согласно формуле Бете, следовательно, уменьшается примерно как v −2 с ростом энергии. Она достигает минимума при приблизительно E = 3 Mc 2 , где M — масса частицы (для протонов это будет примерно при 3000 МэВ). Для высокорелятивистских случаев β ≈ 1 потеря энергии снова увеличивается, логарифмически из-за поперечной составляющей электрического поля.

В теории Бете материал полностью описывается одним числом — средней энергией возбуждения I. В 1933 году Феликс Блох показал, что средняя энергия возбуждения атомов приблизительно определяется выражением
где Z — атомный номер атомов материала. Если ввести это приближение в формулу ( 1 ) выше, то получим выражение, которое часто называют формулой Бете-Блоха . Но поскольку теперь у нас есть точные таблицы I как функции Z (см. ниже), использование такой таблицы даст лучшие результаты, чем использование формулы ( 3 ).
На рисунке показаны нормализованные значения I , взятые из таблицы. [5] Пики и впадины на этом рисунке приводят к соответствующим впадинам и пикам в тормозной способности. Они называются « Z 2 -осцилляциями» или « Z 2 -структурой» (где Z 2 = Z означает атомный номер мишени).
Формула Бете верна только для энергий, достаточно высоких, чтобы заряженная атомная частица ( ион ) не переносила с собой никаких атомных электронов. При меньших энергиях, когда ион переносит электроны, это эффективно снижает его заряд, и тормозная способность, таким образом, уменьшается. Но даже если атом полностью ионизирован, необходимы поправки.
Бете нашел свою формулу, используя квантово-механическую теорию возмущений . Следовательно, его результат пропорционален квадрату заряда z частицы. Описание можно улучшить, рассмотрев поправки, которые соответствуют более высоким степеням z . Это: эффект Баркаса-Андерсена (пропорциональный z 3 , по Вальтеру Х. Баркасу и Гансу Хенрику Андерсену ), и поправка Феликса Блоха (пропорциональная z 4 ). Кроме того, следует учитывать, что атомные электроны пройденного материала не являются стационарными (« оболочечная поправка »).
Упомянутые поправки были встроены, например, в программы PSTAR и ASTAR, с помощью которых можно рассчитать тормозную способность протонов и альфа-частиц. [6] Поправки велики при низкой энергии и становятся все меньше и меньше по мере увеличения энергии.
При очень высоких энергиях необходимо добавлять поправку плотности Ферми [ 5] .