Конверт (математика)

Кривая, внешняя по отношению к семейству кривых в геометрии

Построение огибающей семейства кривых.

В геометрии огибающая плоского семейства кривых — это кривая , которая касается каждого члена семейства в некоторой точке, и эти точки касания вместе образуют всю огибающую. Классически точку на огибающей можно рассматривать как пересечение двух « бесконечно мало смежных» кривых, что означает предел пересечений соседних кривых. Эту идею можно обобщить на огибающую поверхностей в пространстве и так далее до более высоких измерений.

Чтобы иметь огибающую, необходимо, чтобы отдельные члены семейства кривых были дифференцируемыми кривыми , поскольку в противном случае концепция касания не применяется, и должен быть плавный переход, проходящий через членов. Но этих условий недостаточно — данное семейство может не иметь огибающей. Простой пример этого дается семейством концентрических окружностей расширяющегося радиуса.

Огибающая семейства кривых

Пусть каждая кривая C _t в семействе задана как решение уравнения f _t ( x ,  y )=0 (см. неявная кривая ), где t — параметр. Запишем F ( t ,  x ,  y )= f _t ( x ,  y ) и предположим, что F дифференцируема.

Огибающая семейства C _t тогда определяется как множество точек ( x , y ), для которых одновременно ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\partial F \over \partial t}(t,x,y)=0}$

для некоторого значения t , где — частная производная F по t . ^[1] ${\displaystyle \partial F/\partial t}$

Если t и u , t ≠ u — два значения параметра, то пересечение кривых C _t и C _u определяется выражением

${\displaystyle F(t,x,y)=F(u,x,y)=0\,}$

или, что то же самое,

${\displaystyle F(t,x,y)=0~~{\mathsf {and}}~~{\frac {F(u,x,y)-F(t,x,y)}{u-t}}=0.}$

Если u → t, то получим определение, данное выше.

Важный особый случай — когда F ( t ,  x ,  y ) является полиномом от t . Это включает, путем очистки знаменателей , случай, когда F ( t ,  x ,  y ) является рациональной функцией от t . В этом случае определение сводится к тому, что t является двойным корнем F ( t ,  x ,  y ), поэтому уравнение огибающей можно найти, установив дискриминант F равным 0 (потому что определение требует, чтобы F = 0 при некотором t и первая производная = 0, т.е. ее значение 0, и она является min/max при этом t).

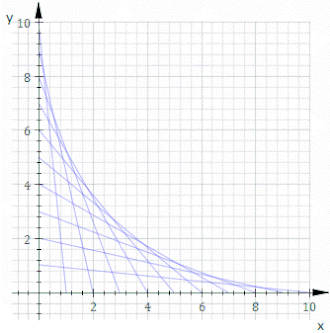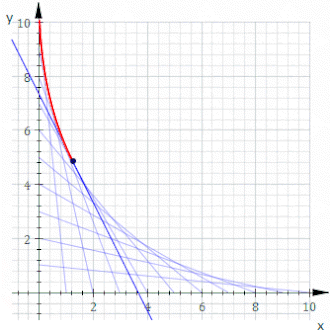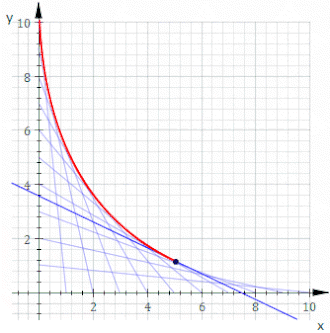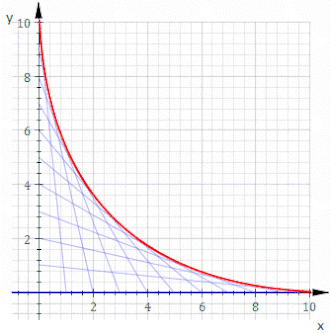
Например, пусть C _t будет линией, пересечения x и y которой равны t и 11− t , это показано на анимации выше. Уравнение C _t имеет вид

${\displaystyle {\frac {x}{t}}+{\frac {y}{11-t}}=1}$

или, очищая дроби,

${\displaystyle x(11-t)+yt-t(11-t)=t^{2}+(-x+y-11)t+11x=0.\,}$

Уравнение огибающей тогда будет иметь вид

${\displaystyle (-x+y-11)^{2}-44x=(x-y)^{2}-22(x+y)+121=0.\,}$

Часто, когда F не является рациональной функцией параметра, ее можно свести к этому случаю с помощью соответствующей подстановки. Например, если семейство задано C _θ с уравнением вида u ( x ,  y )cos θ+ v ( x ,  y )sin θ= w ( x ,  y ), то, положив t = e ^{i θ} , cos θ=( t +1/ t )/2, sin θ=( t -1/ t )/2 i меняет уравнение кривой на

${\displaystyle u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t})=w}$

или

${\displaystyle (u-iv)t^{2}-2wt+(u+iv)=0.\,}$

Уравнение огибающей затем задается путем установки дискриминанта равным 0:

${\displaystyle (u-iv)(u+iv)-w^{2}=0\,}$

или

${\displaystyle u^{2}+v^{2}=w^{2}.\,}$

Альтернативные определения

1. Огибающая E ₁ является пределом пересечений соседних кривых C _t .
2. Огибающая E ₂ представляет собой кривую, касательную ко всем C _t .
3. Огибающая E ₃ является границей области, заполненной кривыми C _t .

Тогда , и , где — множество точек, определенное в начале родительского раздела этого подраздела. ${\displaystyle E_{1}\subseteq {\mathcal {D}}}$ ${\displaystyle E_{2}\subseteq {\mathcal {D}}}$ ${\displaystyle E_{3}\subseteq {\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}}$

Примеры

Пример 1

Эти определения E ₁ , E ₂ и E ₃ огибающей могут быть различными множествами. Рассмотрим, например, кривую y = x ^{3 ,} параметризованную γ : R → R ^{2 ,} где γ( t ) = ( t , t ³ ) . Однопараметрическое семейство кривых будет задано касательными линиями к γ.

Сначала вычисляем дискриминант . Производящая функция: ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,(x,y))=3t^{2}x-y-2t^{3}.}$

Вычисляем частную производную F _t = 6 t ( x – t ) . Отсюда следует, что либо x = t , либо t = 0 . Сначала предположим, что x = t и t ≠ 0 . Подставляем в F: и так, предполагая, что t ≠ 0, следует, что F = F _t = 0 тогда и только тогда, когда ( x , y ) = ( t , t ³ ) . Далее, предполагая, что t = 0 и подставляя в F, получаем F (0,( x , y )) = − y . Итак, предполагая, что t = 0 , следует, что F = F _t = 0 тогда и только тогда, когда y = 0 . Таким образом, дискриминант — это исходная кривая и ее касательная в точке γ(0): ${\displaystyle F(t,(t,y))=t^{3}-y\,}$

${\displaystyle {\mathcal {D}}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\cup \{(x,y)\in \mathbb {R} ^{2}:y=0\}\ .}$

Далее мы вычисляем E ₁ . Одна кривая задается как F ( t ,( x , y )) = 0 , а соседняя кривая задается как F ( t + ε,( x , y )) где ε — некоторое очень малое число. Точка пересечения получается при рассмотрении предела F ( t ,( x , y )) =  F ( t + ε,( x , y )) при ε, стремящемся к нулю. Обратите внимание, что F ( t ,( x , y )) =  F ( t + ε,( x , y )) тогда и только тогда, когда

${\displaystyle L:=F(t,(x,y))-F(t+\varepsilon ,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.}$

Если t ≠ 0 , то L имеет только один множитель ε. Предполагая, что t ≠ 0, то пересечение задается как

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon }}L=6t(t-x)\ .}$

Так как t ≠ 0, то x = t . Значение y вычисляется, зная, что эта точка должна лежать на касательной к исходной кривой γ: F ( t ,( x , y )) = 0. Подстановка и решение дает y = t ³ . Когда t = 0 , L делится на ε ² . Предполагая, что t = 0 , тогда пересечение задается выражением

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}}L=3x\ .}$

Отсюда следует, что x = 0 , и зная, что F ( t ,( x , y )) = 0, получаем y = 0. Отсюда следует, что

${\displaystyle E_{1}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Далее мы вычисляем E ₂ . Сама кривая — это кривая, которая касается всех своих собственных касательных линий. Из этого следует, что

${\displaystyle E_{2}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Наконец, мы вычисляем E ₃ . Каждая точка плоскости имеет по крайней мере одну касательную к γ, проходящую через нее, и поэтому область, заполненная касательными линиями, является всей плоскостью. Граница E ₃ является, таким образом, пустым множеством. Действительно, рассмотрим точку на плоскости, скажем ( x ₀ , y ₀ ). Эта точка лежит на касательной линии тогда и только тогда, когда существует t такое, что

${\displaystyle F(t,(x_{0},y_{0}))=3t^{2}x_{0}-y_{0}-2t^{3}=0\ .}$

Это кубика относительно t и, как таковая, имеет по крайней мере одно действительное решение. Из этого следует, что по крайней мере одна касательная к γ должна проходить через любую заданную точку плоскости. Если y > x ³ и y > 0 , то каждая точка ( x , y ) имеет ровно одну касательную к γ, проходящую через нее. То же самое верно, если y < x ³ y < 0. Если y < x ³ и y > 0 , то каждая точка ( x , y ) имеет ровно три различных касательных к γ, проходящих через нее. То же самое верно, если y > x ³ и y < 0. Если y = x ³ и y ≠ 0 , то каждая точка ( x , y ) имеет ровно две касательные к γ, проходящие через нее (это соответствует кубике, имеющей один обычный корень и один повторный корень). То же самое верно, если y ≠ x ³ и y = 0 . Если y = x ³ и x = 0 , т. е. x = y = 0 , то эта точка имеет единственную касательную к γ , проходящую через нее (это соответствует кубическому уравнению, имеющему один действительный корень кратности 3). Отсюда следует, что

${\displaystyle E_{3}=\varnothing .}$

Пример 2

Этот график дает огибающую семейства линий, соединяющих точки ( t ,0), (0, k - t ), в которых k принимает значение 1.

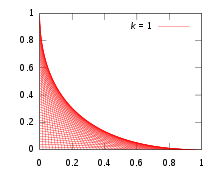
В стринг-арте принято соединять крест-накрест две линии равноудаленных друг от друга штифтов. Какая кривая образуется?

Для простоты установите штифты на осях x и y ; неортогональная компоновка представляет собой вращение и масштабирование . Общая прямая линия соединяет две точки (0, k − t ) и ( t , 0), где k — произвольная масштабная константа, а семейство линий генерируется путем изменения параметра t . Из простой геометрии уравнение этой прямой линии имеет вид y = −( k  −  t ) x / t + k  −  t . Перестановка и приведение к виду F ( x , y , t ) = 0 дает:

Теперь дифференцируем F ( x , y , t ) по t и приравниваем результат к нулю, чтобы получить

Эти два уравнения совместно определяют уравнение огибающей. Из (2) имеем:

${\displaystyle t={\sqrt {kx}}\,}$

Подставляя это значение t в (1) и упрощая, получаем уравнение для огибающей:

Или, переформулировав в более элегантную форму, показывающую симметрию между x и y:

Мы можем взять поворот осей, где ось b - это линия y=x, ориентированная на северо-восток, а ось a - это линия y =− x, ориентированная на юго-восток. Эти новые оси связаны с исходными осями xy соотношениями x =( b + a )/ √ 2 и y =( b − a )/ √ 2 . После подстановки в (4), расширения и упрощения получаем

что, по-видимому, является уравнением параболы с осью вдоль a = 0, или y = x .

Пример 3

Пусть I ⊂ R — открытый интервал, а γ : I → R ² — гладкая плоская кривая, параметризованная длиной дуги . Рассмотрим однопараметрическое семейство нормальных линий к γ( I ). Прямая нормальна к γ в точке γ( t ), если она проходит через γ( t ) и перпендикулярна касательному вектору к γ в точке γ( t ). Пусть T обозначает единичный касательный вектор к γ, а N — единичный нормальный вектор . Используя точку для обозначения скалярного произведения , порождающее семейство для однопараметрического семейства нормальных линий задается как F  : I × R ² → R , где

${\displaystyle F(t,{\mathbf {x} })=({\mathbf {x} }-\gamma (t))\cdot {\mathbf {T} }(t)\ .}$

Очевидно, что ( x − γ)· T = 0 тогда и только тогда, когда x − γ перпендикулярен T, или, что эквивалентно, тогда и только тогда, когда x − γ параллелен N , или , что эквивалентно , тогда и только тогда, когда x = γ + λ N для некоторого λ ∈ R. Отсюда следует, что

${\displaystyle L_{t_{0}}:=\{{\mathbf {x} }\in \mathbb {R} ^{2}:F(t_{0},{\mathbf {x} })=0\}}$

является в точности нормальной линией к γ в точке γ( t ₀ ). Чтобы найти дискриминант F, нам нужно вычислить его частную производную по t :

${\displaystyle {\frac {\partial F}{\partial t}}(t,{\mathbf {x} })=\kappa (t)({\mathbf {x} }-\gamma (t))\cdot {\mathbf {N} }(t)-1\ ,}$

где κ — кривизна плоской кривой γ. Было замечено, что F = 0 тогда и только тогда, когда x - γ = λ N для некоторого λ ∈ R. Предполагая, что F = 0, получаем

${\displaystyle {\frac {\partial F}{\partial t}}=\lambda \kappa (t)-1\ .}$

Предполагая, что κ ≠ 0, следует, что λ = 1/κ и поэтому

${\displaystyle {\mathcal {D}}=\gamma (t)+{\frac {1}{\kappa (t)}}{\mathbf {N} }(t)\ .}$

Это и есть эволюция кривой γ.

Пример 4

Астроида как огибающая семейства линий, соединяющих точки ( s ,0), ​​(0 ^, t ) при s2  +  t2  = ¹

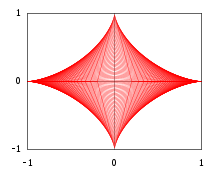
Следующий пример показывает, что в некоторых случаях огибающая семейства кривых может рассматриваться как топологическая граница объединения множеств, границы которых являются кривыми огибающей. Для и рассмотрим (открытый) прямоугольный треугольник в декартовой плоскости с вершинами , и ${\displaystyle s>0}$ ${\displaystyle t>0}$ ${\displaystyle (0,0)}$ ${\displaystyle (s,0)}$ ${\displaystyle (0,t)}$

${\displaystyle T_{s,t}:=\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}<1\right\}.}$

Зафиксируем показатель степени и рассмотрим объединение всех треугольников, на которые распространяется ограничение , то есть открытое множество. ${\displaystyle \alpha >0}$ ${\displaystyle T_{s,t}}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle \Delta _{\alpha }:=\bigcup _{s^{\alpha }+t^{\alpha }=1}T_{s,t}.}$

Чтобы написать декартово представление для , начните с любого , удовлетворяющего и любого . Неравенство Гёльдера относительно сопряженных показателей и дает: ${\displaystyle \textstyle \Delta _{\alpha }}$ ${\displaystyle \textstyle s>0}$ ${\displaystyle \textstyle t>0}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$ ${\displaystyle \textstyle (x,y)\in \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \mathbb {R} ^{2}}$ ${\displaystyle p:=1+{\frac {1}{\alpha }}}$ ${\displaystyle \textstyle q:={1+\alpha }}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+t^{\alpha }{\Big )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}}$,

с равенством тогда и только тогда, когда . В терминах объединения множеств последнее неравенство гласит: точка принадлежит множеству , то есть она принадлежит некоторому с , тогда и только тогда, когда она удовлетворяет ${\displaystyle \textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}}$ ${\displaystyle (x,y)\in \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \Delta _{\alpha }}$ ${\displaystyle \textstyle T_{s,t}}$ ${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}<1.}$

При этом граница множества является огибающей соответствующего семейства отрезков прямых ${\displaystyle \mathbb {R} _{+}^{2}}$ ${\displaystyle \textstyle \Delta _{\alpha }}$

${\displaystyle \left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}=1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1}$

(то есть гипотенузы треугольников) и имеет декартово уравнение

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}=1.}$

Обратите внимание, что, в частности, значение дает дугу параболы примера 2, а значение (означающее, что все гипотенузы являются отрезками единичной длины) дает астроиду . ${\displaystyle \alpha =1}$ ${\displaystyle \alpha =2}$

Пример 5

Огибающая орбит снарядов (при постоянной начальной скорости) представляет собой вогнутую параболу. Начальная скорость 10 м/с. Примем g = 10 м/с ² .

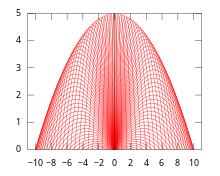
Рассмотрим следующий пример оболочки в движении. Предположим, что на начальной высоте 0 в воздух бросают снаряд с постоянной начальной скоростью v, но разными углами возвышения θ. Пусть x будет горизонтальной осью на поверхности движения, а y обозначит вертикальную ось. Тогда движение дает следующую дифференциальную динамическую систему :

${\displaystyle {\frac {d^{2}y}{dt^{2}}}=-g,\;{\frac {d^{2}x}{dt^{2}}}=0,}$

который удовлетворяет четырем начальным условиям :

${\displaystyle {\frac {dx}{dt}}{\bigg |}_{t=0}=v\cos \theta ,\;{\frac {dy}{dt}}{\bigg |}_{t=0}=v\sin \theta ,\;x{\bigg |}_{t=0}=y{\bigg |}_{t=0}=0.}$

Здесь t обозначает время движения, θ — угол возвышения, g обозначает ускорение свободного падения , а v — постоянная начальная скорость (не скорость ). Решение указанной выше системы может иметь неявный вид :

${\displaystyle F(x,y,\theta )=x\tan \theta -{\frac {gx^{2}}{2v^{2}\cos ^{2}\theta }}-y=0.}$

Чтобы найти уравнение огибающей, можно вычислить искомую производную:

${\displaystyle {\frac {\partial F}{\partial \theta }}={\frac {x}{\cos ^{2}\theta }}-{\frac {gx^{2}\tan \theta }{v^{2}\cos ^{2}\theta }}=0.}$

Исключив θ, можно прийти к следующему уравнению огибающей:

${\displaystyle y={\frac {v^{2}}{2g}}-{\frac {g}{2v^{2}}}x^{2}.}$

Очевидно, что полученная огибающая также представляет собой вогнутую параболу .

Огибающая семейства поверхностей

Однопараметрическое семейство поверхностей в трехмерном евклидовом пространстве задается набором уравнений

${\displaystyle F(x,y,z,a)=0}$

в зависимости от действительного параметра a . ^[2] Например, касательные плоскости к поверхности вдоль кривой на поверхности образуют такое семейство.

Две поверхности, соответствующие разным значениям a и a', пересекаются по общей кривой, определяемой соотношением

${\displaystyle F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\prime })-F(x,y,z,a) \over a^{\prime }-a}=0.}$

В пределе, когда a' приближается к a , эта кривая стремится к кривой, содержащейся на поверхности в точке a.

${\displaystyle F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.}$

Эта кривая называется характеристикой семейства при a . При изменении a геометрическое место этих характеристических кривых определяет поверхность, называемую огибающей семейства поверхностей.

Огибающая семейства поверхностей касается каждой поверхности семейства вдоль характеристической кривой этой поверхности.

Обобщения

Идея оболочки семейства гладких подмногообразий следует естественным образом. В общем случае, если у нас есть семейство подмногообразий с коразмерностью c , то нам нужно иметь по крайней мере c -параметрическое семейство таких подмногообразий. Например: однопараметрическое семейство кривых в трехмерном пространстве ( c = 2) в общем случае не имеет оболочки.

Приложения

Обыкновенные дифференциальные уравнения

Огибающие связаны с изучением обыкновенных дифференциальных уравнений (ОДУ) и, в частности, сингулярных решений ОДУ. ^[3] Рассмотрим, например, однопараметрическое семейство касательных к параболе y = x ² . Они задаются порождающим семейством F ( t ,( x , y )) = t ² – 2 tx + y . Нулевой уровень F ( t ₀ ,( x , y )) = 0 дает уравнение касательной к параболе в точке ( t ₀ , t ₀ ² ). Уравнение t ² – 2 tx + y = 0 всегда можно решить относительно y как функции x , поэтому рассмотрим

${\displaystyle t^{2}-2tx+y(x)=0.\ }$

Заменяя

${\displaystyle t=\left({\frac {dy}{dx}}\right)/2}$

дает ОДУ

${\displaystyle \left({\frac {dy}{dx}}\right)^{2}\!\!-4x{\frac {dy}{dx}}+4y=0.}$

Неудивительно, что y  = 2 tx  −  t ^{2 —} все решения этого ОДУ. Однако огибающая этого однопараметрического семейства линий, которая является параболой y  =  x ² , также является решением этого ОДУ. Другим известным примером является уравнение Клеро .

Уравнения с частными производными

Огибающие могут использоваться для построения более сложных решений уравнений в частных производных первого порядка (УЧП) из более простых. ^[4] Пусть F ( x , u ,D u ) = 0 будет УЧП первого порядка, где x — переменная со значениями в открытом множестве Ω ⊂  R ⁿ , u — неизвестная вещественная функция, D u — градиент u , а F — непрерывно дифференцируемая функция, которая регулярна в D u . Предположим, что u ( x ; a ) — это m -параметрическое семейство решений: то есть для каждого фиксированного a  ∈  A  ⊂  R ^m , u ( x ; a ) является решением дифференциального уравнения. Новое решение дифференциального уравнения можно построить, сначала решив (если возможно)

${\displaystyle D_{a}u(x;a)=0\,}$

для a  = φ( x ) как функции x . Огибающая семейства функций { u (·, a )} _{a ∈ A} определяется как

${\displaystyle v(x)=u(x;\varphi (x)),\quad x\in \Omega ,}$

а также решает дифференциальное уравнение (при условии, что оно существует как непрерывно дифференцируемая функция).

Геометрически график v ( x ) всюду касается графика некоторого члена семейства u ( x ; a ). Поскольку дифференциальное уравнение имеет первый порядок, оно накладывает условие только на касательную плоскость к графику, так что любая функция, всюду касательная к решению, также должна быть решением. Та же идея лежит в основе решения уравнения первого порядка как интеграла конуса Монжа . ^[5] Конус Монжа представляет собой поле конуса в R ^{n +1} переменных ( x , u ), вырезанное оболочкой касательных пространств к УЧП первого порядка в каждой точке. Тогда решение УЧП является оболочкой поля конуса.

В римановой геометрии , если гладкое семейство геодезических, проходящее через точку P в римановом многообразии, имеет огибающую, то P имеет сопряженную точку , в которой любая геодезическая семейства пересекает огибающую. То же самое верно в более общем смысле в вариационном исчислении : если семейство экстремалей функционала, проходящего через заданную точку P, имеет огибающую, то точка, в которой экстремаль пересекает огибающую , является сопряженной точкой к P.

Каустики

Отражательная каустика, образованная окружностью и параллельными лучами

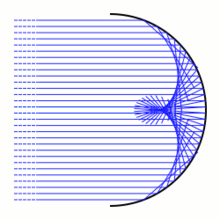
В геометрической оптике каустика — это огибающая семейства световых лучей . На этой картинке изображена дуга окружности. Световые лучи (показаны синим цветом) исходят из источника, находящегося в бесконечности , и поэтому идут параллельно. Когда они попадают на дугу окружности, световые лучи рассеиваются в разных направлениях в соответствии с законом отражения . Когда световой луч попадает на дугу в точке, свет будет отражаться так, как если бы он был отражен касательной дуги в этой точке. Отраженные световые лучи дают однопараметрическое семейство линий на плоскости. Огибающая этих линий — отражательная каустика . Отражательная каустика в общем случае будет состоять из гладких точек и обычных точек возврата.

С точки зрения вариационного исчисления принцип Ферма (в его современной форме) подразумевает, что световые лучи являются экстремалями для функционала длины

${\displaystyle L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt}$

среди гладких кривых γ на [ a , b ] с фиксированными конечными точками γ( a ) и γ( b ). Каустика, определяемая заданной точкой P ( на изображении точка находится на бесконечности), представляет собой множество сопряженных точек к P. ^[6]

принцип Гюйгенса

Свет может проходить через анизотропные неоднородные среды с разной скоростью в зависимости от направления и начального положения светового луча. Граница множества точек, до которых свет может дойти из заданной точки q за время t, известна как волновой фронт за время t , обозначаемый здесь как Φ _q ( t ). Она состоит именно из тех точек, которых можно достичь из q за время t, двигаясь со скоростью света. Принцип Гюйгенса утверждает, что множество волновых фронтов Φ _{q 0} ( s + t ) является огибающей семейства волновых фронтов Φ _q ( s ) для q  ∈ Φ _{q 0} ( t ). В более общем смысле, точка q ₀ может быть заменена любой кривой, поверхностью или замкнутым множеством в пространстве. ^[7]

Смотрите также

• Каустик (математика)
• Теорема о конверте
• Линейчатая поверхность

Ссылки

1. Брюс, Дж. В.; Гиблин, П. Дж. (1984), Кривые и особенности , Cambridge University Press, ISBN 0-521-42999-4
2. Эйзенхарт, Лютер П. (2008), Трактат о дифференциальной геометрии кривых и поверхностей , Schwarz Press, ISBN 1-4437-3160-9
3. Форсайт, Эндрю Рассел (1959), Теория дифференциальных уравнений , Шесть томов, связанных в три, Нью-Йорк: Dover Publications , MR  0123757, §§100-106.
4. Эванс, Лоуренс К. (1998), Уравнения с частными производными , Провиденс, Род-Айленд: Американское математическое общество , ISBN 978-0-8218-0772-9.
5. Джон, Фриц (1991), Уравнения с частными производными (4-е изд.), Springer, ISBN 978-0-387-90609-6.
6. Борн, Макс (октябрь 1999 г.), Принцип оптики , Cambridge University Press , ISBN 978-0-521-64222-4, Приложение I: Вариационное исчисление.
7. Арнольд, VI (1997), Математические методы классической механики, 2-е изд. , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-96890-2, §46.

Внешние ссылки

• Вайсштейн, Эрик В. «Конверт». Математический мир .
• «Огибающая семейства плоских кривых» на MathCurve.