Хэш-таблица

Ассоциативный массив для хранения пар ключ-значение

Небольшая телефонная книга в виде хеш-таблицы

В вычислительной технике хэш -таблица — это структура данных , реализующая ассоциативный массив , также называемый словарем или просто картой ; ассоциативный массив — это абстрактный тип данных , который сопоставляет ключи со значениями . ^[2] Хэш-таблица использует хэш-функцию для вычисления индекса , также называемого хэш-кодом , в массиве контейнеров или слотов , из которого можно найти нужное значение. Во время поиска ключ хэшируется, и полученный хэш указывает, где хранится соответствующее значение. Карта, реализованная хэш-таблицей, называется хэш-картой .

Большинство конструкций хэш-таблиц используют несовершенную хэш-функцию . Коллизии хэш-функций , когда хэш-функция генерирует один и тот же индекс для более чем одного ключа, как правило, должны быть каким-то образом учтены.

В хорошо размерной хэш-таблице средняя временная сложность для каждого поиска не зависит от количества элементов, хранящихся в таблице. Многие конструкции хэш-таблиц также допускают произвольные вставки и удаления пар ключ-значение , при амортизированной постоянной средней стоимости за операцию. ^{[3] [4] [5]}

Хеширование является примером компромисса между пространством и временем . Если память бесконечна, весь ключ может быть использован непосредственно в качестве индекса для поиска его значения с помощью одного доступа к памяти. С другой стороны, если доступно бесконечное время, значения могут храниться независимо от их ключей, и для извлечения элемента может использоваться двоичный поиск или линейный поиск . ^{[6] : 458}

Во многих ситуациях хэш-таблицы оказываются в среднем более эффективными, чем деревья поиска или любая другая структура поиска в таблице . По этой причине они широко используются во многих видах компьютерного программного обеспечения , особенно для ассоциативных массивов , индексации баз данных , кэшей и наборов .

История

Идея хеширования возникла независимо в разных местах. В январе 1953 года Ганс Петер Лун написал внутренний меморандум IBM , в котором использовалось хеширование с цепочкой. Первый пример открытой адресации был предложен AD Linh, основанный на меморандуме Луна. ^{[4] : 547} Примерно в то же время Gene Amdahl , Elaine M. McGraw , Nathaniel Rochester и Arthur Samuel из IBM Research реализовали хеширование для ассемблера IBM 701. ^{[7] : 124} Открытая адресация с линейным зондированием приписывается Amdahl, хотя та же идея независимо возникла у Андрея Ершова . ^{[7] : 124–125} Термин «открытая адресация» был придуман W. Wesley Peterson в его статье, в которой обсуждается проблема поиска в больших файлах. ^{[8] : 15}

Первая опубликованная работа по хешированию с цепочкой приписывается Арнольду Дюмею , который обсуждал идею использования остатка по модулю простого числа в качестве хеш-функции. ^{[8] : 15} Слово «хеширование» впервые было опубликовано в статье Роберта Морриса. ^{[7] : 126} Теоретический анализ линейного зондирования был первоначально представлен Конхеймом и Вайсом. ^{[8] : 15}

Обзор

Ассоциативный массив хранит набор пар (ключ, значение) и позволяет выполнять вставку, удаление и поиск (search) с ограничением уникальных ключей . В реализации ассоциативных массивов в виде хэш-таблицы массив длины частично заполнен элементами, где . Значение сохраняется в индексном месте , где — хэш-функция, а . ^{[8] : 2} При разумных предположениях хэш-таблицы имеют лучшие временные границы сложности для операций поиска, удаления и вставки по сравнению с самобалансирующимися бинарными деревьями поиска . ^{[8] : 1} ${\displaystyle A}$ ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle m\geq n}$ ${\displaystyle x}$ ${\displaystyle A[h(x)]}$ ${\displaystyle h}$ ${\displaystyle h(x)<m}$

Хэш-таблицы также часто используются для реализации наборов, при этом опускается сохраненное значение для каждого ключа и просто отслеживается наличие ключа. ^{[8] : 1}

Коэффициент нагрузки

Коэффициент загрузки является критической статистикой хэш-таблицы и определяется следующим образом: ^[1] где ${\displaystyle \alpha }$ $${\displaystyle {\text{load factor}}\ (\alpha )={\frac {n}{m}},}$$

• ${\displaystyle n}$— количество записей, занятых в хэш-таблице.
• ${\displaystyle m}$это количество ведер.

Производительность хэш-таблицы ухудшается в зависимости от коэффициента загрузки . ^{[8] : 2} ${\displaystyle \alpha }$

Программное обеспечение обычно обеспечивает, чтобы коэффициент загрузки оставался ниже определенной константы, . Это помогает поддерживать хорошую производительность. Поэтому распространенный подход заключается в изменении размера или «перехешировании» хэш-таблицы всякий раз, когда коэффициент загрузки достигает . Аналогичным образом таблица также может быть изменена в размере, если коэффициент загрузки падает ниже . ^[9] ${\displaystyle \alpha }$ ${\displaystyle \alpha _{\max }}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha _{\max }}$ ${\displaystyle \alpha _{\max }/4}$

Коэффициент нагрузки для раздельного соединения

При использовании отдельных цепочек хэш-таблиц каждый слот массива блоков хранит указатель на список или массив данных. ^[10]

Отдельные цепочки хэш-таблиц постепенно снижают производительность по мере роста коэффициента загрузки, и не существует фиксированной точки, после которой изменение размера становится абсолютно необходимым. ^[9]

При раздельном объединении в цепочку значение, дающее наилучшую производительность, обычно находится в диапазоне от 1 до 3. ^[9] ${\displaystyle \alpha _{\max }}$

Коэффициент нагрузки для открытой адресации

При открытой адресации каждый слот массива bucket содержит ровно один элемент. Поэтому хэш-таблица с открытой адресацией не может иметь коэффициент загрузки больше 1. ^[10]

Производительность открытой адресации становится очень низкой, когда коэффициент загрузки приближается к 1. ^[9]

Поэтому хэш-таблица, использующая открытую адресацию, должна быть изменена в размере или перехеширована, если коэффициент загрузки приближается к 1. ^[9] ${\displaystyle \alpha }$

При открытой адресации приемлемые значения максимального коэффициента загрузки должны находиться в диапазоне от 0,6 до 0,75. ^{[11] [12] : 110} ${\displaystyle \alpha _{\max }}$

Функция хэширования

Функция хэширования отображает вселенную ключей в индексы или слоты в таблице, то есть для . Традиционные реализации функций хэширования основаны на предположении целочисленной вселенной , что все элементы таблицы происходят из вселенной , где длина бита ограничена размером слова компьютерной архитектуры . ^{[8] : 2} ${\displaystyle h:U\rightarrow \{0,...,m-1\}}$ ${\displaystyle U}$ ${\displaystyle h(x)\in \{0,...,m-1\}}$ ${\displaystyle x\in U}$ ${\displaystyle U=\{0,...,u-1\}}$ ${\displaystyle u}$

Говорят, что хеш-функция идеальна для заданного множества, если она инъективна на , то есть если каждый элемент отображается на различное значение в . ^{[13] [14]} Идеальную хеш-функцию можно создать, если все ключи известны заранее. ^[13] ${\displaystyle h}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle x\in S}$ ${\displaystyle {0,...,m-1}}$

Предположение о целочисленной вселенной

Схемы хеширования, используемые в предположении целочисленной вселенной, включают хеширование делением, хеширование умножением, универсальное хеширование , динамическое совершенное хеширование и статическое совершенное хеширование . ^{[8] : 2} Однако хеширование делением является наиболее часто используемой схемой. ^{[15] : 264  [12] : 110}

Хеширование путем деления

Схема хеширования делением выглядит следующим образом: ^{[8] : 2} где — значение хеш-функции , а — размер таблицы. $${\displaystyle h(x)\ =\ x\,{\bmod {\,}}m}$$ ${\displaystyle h(x)}$ ${\displaystyle x\in S}$ ${\displaystyle m}$

Хеширование путем умножения

Схема хеширования умножением выглядит следующим образом: ^{[8] : 2–3} Где — нецелая вещественная константа , а — размер таблицы. Преимущество хеширования умножением в том, что не является критическим. ^{[8] : 2–3} Хотя любое значение создает хеш-функцию, Дональд Кнут предлагает использовать золотое сечение . ^{[8] : 3} $${\displaystyle h(x)=\lfloor m{\bigl (}(xA){\bmod {1}}{\bigr )}\rfloor }$$ ${\displaystyle A}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle A}$

Выбор хэш-функции

Равномерное распределение значений хэша является фундаментальным требованием хэш-функции. Неравномерное распределение увеличивает количество коллизий и стоимость их разрешения. Равномерность иногда трудно обеспечить с помощью дизайна, но ее можно оценить эмпирически с помощью статистических тестов, например, критерия хи-квадрат Пирсона для дискретных равномерных распределений. ^{[16] [17]}

Распределение должно быть равномерным только для размеров таблиц, которые встречаются в приложении. В частности, если используется динамическое изменение размера с точным удвоением и делением пополам размера таблицы, то хэш-функция должна быть равномерна только тогда, когда размер является степенью двойки . Здесь индекс может быть вычислен как некоторый диапазон битов хэш-функции. С другой стороны, некоторые алгоритмы хэширования предпочитают, чтобы размер был простым числом . ^[18]

Для схем открытой адресации хэш-функция также должна избегать кластеризации , сопоставления двух или более ключей с последовательными слотами. Такая кластеризация может привести к резкому росту стоимости поиска, даже если коэффициент загрузки низок, а коллизии редки. Утверждается, что популярный мультипликативный хэш имеет особенно плохое поведение кластеризации. ^{[18] [4]}

K-независимое хеширование предлагает способ доказать, что определенная хеш-функция не имеет плохих наборов ключей для заданного типа хеш-таблицы. Ряд результатов K-независимости известны для схем разрешения коллизий, таких как линейное зондирование и хеширование кукушки. Поскольку K-независимость может доказать, что хеш-функция работает, можно сосредоточиться на поиске максимально быстрой такой хеш-функции. ^[19]

Разрешение столкновений

Алгоритм поиска, использующий хеширование, состоит из двух частей. Первая часть вычисляет хеш-функцию , которая преобразует ключ поиска в индекс массива . Идеальный случай — это когда никакие два ключа поиска не хешируются в один и тот же индекс массива. Однако это не всегда так и невозможно гарантировать для невидимых данных. ^{[20] : 515} Следовательно, вторая часть алгоритма — разрешение коллизий. Два распространенных метода разрешения коллизий — это раздельное связывание и открытая адресация. ^{[6] : 458}

Раздельное цепочкование

Коллизия хэшей решена путем раздельного объединения в цепочку

Коллизия хэшей путем отдельного объединения в цепочку с записями заголовка в массиве контейнеров.

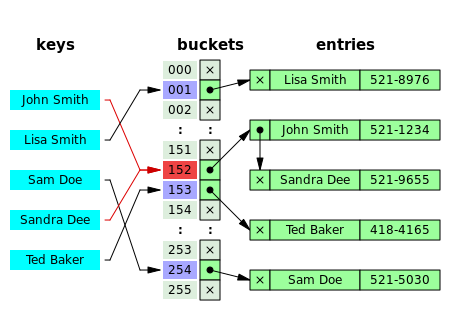
В раздельной цепочке процесс включает построение связанного списка с парой ключ-значение для каждого индекса массива поиска. Сталкивающиеся элементы связываются вместе через один связанный список, который можно просмотреть для доступа к элементу с уникальным ключом поиска. ^{[6] : 464} Разрешение коллизий посредством связывания со связанным списком является распространенным методом реализации хэш-таблиц. Пусть и будут хэш-таблицей и узлом соответственно, операция включает следующее: ^{[15] : 258} ${\displaystyle T}$ ${\displaystyle x}$

Chained-Hash-Insert( T , k ) вставляет  x  в начало связанного списка  T [ h ( k )]Chained-Hash-Search( T , k ) ищет элемент с ключом  k  в связанном списке  T [ h ( k )]Chained-Hash-Delete( T , k ) удалить  x  из связанного списка  T [ h ( k )]

Если элемент сопоставим либо численно , либо лексически и вставлен в список с сохранением общего порядка , это приводит к более быстрому завершению безуспешных поисков. ^{[20] : 520–521}

Другие структуры данных для раздельного объединения в цепочку

Если ключи упорядочены , может быть эффективным использование « самоорганизующихся » концепций, таких как использование самобалансирующегося бинарного дерева поиска , с помощью которого теоретически наихудший случай может быть сведен к , хотя это вносит дополнительные сложности. ^{[20] : 521} ${\displaystyle O(\log {n})}$

В динамическом идеальном хешировании двухуровневые хеш-таблицы используются для снижения сложности поиска, чтобы гарантировать ее в худшем случае. В этой технике блоки записей организованы как идеальные хеш-таблицы со слотами, обеспечивающими постоянное время поиска в худшем случае и низкое амортизированное время для вставки. ^[21] Исследование показывает, что раздельное цепочечное связывание на основе массива на 97% более производительно по сравнению со стандартным методом связанного списка при большой нагрузке. ^{[22] : 99} ${\displaystyle O(1)}$ ${\displaystyle k}$ ${\displaystyle k^{2}}$

Такие методы, как использование дерева слияния для каждого сегмента, также приводят к постоянному времени для всех операций с высокой вероятностью. ^[23]

Кэширование и локальность ссылок

Связанный список отдельной реализации цепочки может не учитывать кэш из- за пространственной локальности — локальности ссылок — когда узлы связанного списка разбросаны по памяти, поэтому обход списка во время вставки и поиска может повлечь за собой неэффективность кэша ЦП . ^{[22] : 91}

В вариантах разрешения коллизий с учетом кэширования посредством раздельного связывания динамический массив, который, как оказалось, более дружелюбен к кэшированию, используется в том месте, где обычно развертываются связанный список или самобалансирующиеся двоичные деревья поиска, поскольку непрерывный шаблон распределения массива может быть использован предварительными выборками аппаратного кэша , такими как буфер трансляции , что приводит к сокращению времени доступа и потребления памяти. ^{[24] [25] [26]}

Открытая адресация

Коллизия хэшей разрешена открытой адресацией с линейным зондированием (интервал=1). Обратите внимание, что у "Ted Baker" уникальный хэш, но тем не менее он столкнулся с "Sandra Dee", который ранее столкнулся с "John Smith".

Этот график сравнивает среднее количество промахов кэша ЦП, необходимых для поиска элементов в больших хэш-таблицах (намного превышающих размер кэша) с цепочкой и линейным зондированием. Линейное зондирование работает лучше из-за лучшей локальности ссылок , хотя по мере заполнения таблицы его производительность резко падает.

Открытая адресация — это еще один метод разрешения коллизий, в котором каждая запись записи хранится в самом массиве ведер, а разрешение хеша выполняется посредством зондирования . Когда необходимо вставить новую запись, ведра проверяются, начиная со слота hashed-to и продолжая в некоторой последовательности зондирования , пока не будет найден свободный слот. При поиске записи ведра сканируются в той же последовательности, пока не будет найдена целевая запись или неиспользуемый слот массива, что указывает на неудачный поиск. ^[27]

Известные последовательности зондов включают в себя:

• Линейное зондирование , при котором интервал между зондами фиксирован (обычно 1). ^[28]
• Квадратичное зондирование , при котором интервал между зондами увеличивается путем добавления последовательных выходов квадратичного полинома к значению, полученному в результате исходного вычисления хэша. ^{[29] : 272}
• Двойное хеширование , при котором интервал между зондами вычисляется с помощью вторичной хеш-функции. ^{[29] : 272–273}

Производительность открытой адресации может быть ниже по сравнению с раздельной цепочкой, поскольку последовательность зондирования увеличивается, когда коэффициент загрузки приближается к 1. ^{[9] [22] : 93} Зондирование приводит к бесконечному циклу , если коэффициент загрузки достигает 1 в случае полностью заполненной таблицы. ^{[6] : 471} Средняя стоимость линейного зондирования зависит от способности хэш-функции равномерно распределять элементы по всей таблице, чтобы избежать кластеризации , поскольку образование кластеров приведет к увеличению времени поиска. ^{[6] : 472} ${\displaystyle \alpha }$

Кэширование и локальность ссылок

Поскольку слоты расположены в последовательных местах, линейное зондирование может привести к лучшему использованию кэша ЦП из-за локальности ссылок, что приводит к уменьшению задержки памяти . ^[28]

Другие методы разрешения коллизий, основанные на открытой адресации

Объединенное хеширование

Объединенное хеширование представляет собой гибрид как отдельной цепочки, так и открытой адресации, в которой блоки или узлы связаны внутри таблицы. ^{[30] : 6–8} Алгоритм идеально подходит для фиксированного выделения памяти . ^{[30] : 4} Коллизия в объединенном хешировании разрешается путем идентификации пустого слота с наибольшим индексом в хеш-таблице, затем в этот слот вставляется коллизионное значение. Блок также связан со слотом вставленного узла, который содержит его коллизионный хеш-адрес. ^{[30] : 8}

Кукушкино хеширование

Кукушечное хеширование — это форма метода разрешения коллизий с открытой адресацией, которая гарантирует сложность поиска в худшем случае и постоянное амортизированное время для вставок. Коллизия разрешается путем поддержания двух хеш-таблиц, каждая из которых имеет свою собственную хеш-функцию, и конфликтующий слот заменяется заданным элементом, а занятый элемент слота перемещается в другую хеш-таблицу. Процесс продолжается до тех пор, пока каждый ключ не займет свое место в пустых ячейках таблиц; если процедура входит в бесконечный цикл — что идентифицируется путем поддержания порогового счетчика циклов — обе хеш-таблицы перехешируются с новыми хеш-функциями, и процедура продолжается. ^{[31] : 124–125} ${\displaystyle O(1)}$

Классики хэширование

Классическое хеширование — это алгоритм с открытой адресацией, который объединяет элементы кукушкиного хеширования , линейного зондирования и цепочек через понятие соседства ведер — последовательных ведер вокруг любого данного занятого ведра, также называемого «виртуальным» ведерком. ^{[32] : 351–352} Алгоритм разработан для обеспечения лучшей производительности, когда коэффициент загрузки хеш-таблицы превышает 90%; он также обеспечивает высокую пропускную способность в параллельных настройках , поэтому хорошо подходит для реализации изменяемого размера параллельной хеш-таблицы . ^{[32] : 350} Характеристика соседства классического хеширования гарантирует свойство, заключающееся в том, что стоимость поиска нужного элемента из любых заданных ведер в пределах соседства очень близка к стоимости его поиска в самом ведерке; алгоритм пытается быть элементом в его соседстве — с возможными затратами, связанными с перемещением других элементов. ^{[32] : 352}

Каждый контейнер в хэш-таблице включает в себя дополнительную «информацию о прыжке» — битовый массив размером H для указания относительного расстояния элемента, который был изначально хэширован в текущий виртуальный контейнер в пределах H -1 записей. ^{[32] : 352} Пусть и будут ключом для вставки и контейнером, в который хэшируется ключ, соответственно; в процедуру вставки вовлечено несколько случаев, так что свойство соседства алгоритма является обязательным: ^{[32] : 352–353} если пуст, элемент вставляется, а самый левый бит битовой карты устанавливается в 1; если не пуст, используется линейное зондирование для поиска пустой ячейки в таблице, битовая карта контейнера обновляется с последующей вставкой; если пустой слот не находится в пределах диапазона соседства , т. е . H -1, последующая своп-обработка и манипуляция битовым массивом информации о прыжке для каждого контейнера выполняется в соответствии с его инвариантными свойствами соседства . ^{[32] : 353} ${\displaystyle k}$ ${\displaystyle Bk}$ ${\displaystyle Bk}$

Робин Гуд хеширование

Хеширование Робин Гуда — это алгоритм разрешения коллизий на основе открытой адресации; коллизии разрешаются путем предпочтения смещения элемента, который находится дальше всего — или имеет самую большую длину последовательности зонда (PSL) — от его «домашнего местоположения», т. е. контейнера, в который был хэширован элемент. ^{[33] : 12} Хотя хеширование Робин Гуда не изменяет теоретическую стоимость поиска , оно существенно влияет на дисперсию распределения элементов в контейнерах, ^{[34] : 2,} т. е. имеет дело с формированием кластера в хэш-таблице. ^[35] Каждый узел в хэш-таблице, использующий хэширование Робин Гуда, должен быть расширен для хранения дополнительного значения PSL. ^[36] Пусть будет ключом для вставки, будет (инкрементной) длиной PSL , будет хэш-таблицей и будет индексом, процедура вставки выглядит следующим образом: ^{[33] : 12–13  [37] : 5} ${\displaystyle x}$ ${\displaystyle x.psl}$ ${\displaystyle x}$ ${\displaystyle T}$ ${\displaystyle j}$

• Если : итерация переходит к следующему блоку без попытки внешнего зондирования. ${\displaystyle x.psl\ \leq \ T[j].psl}$
• Если : вставьте элемент в контейнер ; поменяйте местами с — пусть будет ; продолжите зондирование из первого контейнера для вставки ; повторите процедуру, пока не будут вставлены все элементы. ${\displaystyle x.psl\ >\ T[j].psl}$ ${\displaystyle x}$ ${\displaystyle j}$ ${\displaystyle x}$ ${\displaystyle T[j]}$ ${\displaystyle x'}$ ${\displaystyle j+1}$ ${\displaystyle x'}$

Динамическое изменение размера

Повторные вставки приводят к росту числа записей в хэш-таблице, что, соответственно, увеличивает коэффициент загрузки; для поддержания амортизированной производительности операций поиска и вставки хэш-таблица динамически изменяет размер, а элементы таблиц повторно хэшируются в сегменты новой хэш-таблицы, ^[9] поскольку элементы не могут быть скопированы, поскольку изменение размеров таблиц приводит к разному значению хэша из-за операции по модулю . ^[38] Если хэш-таблица становится «слишком пустой» после удаления некоторых элементов, можно выполнить изменение размера, чтобы избежать чрезмерного использования памяти . ^[39] ${\displaystyle O(1)}$

Изменение размера путем перемещения всех записей

Обычно новая хэш-таблица с размером, вдвое превышающим размер исходной хэш-таблицы, выделяется в частном порядке, и каждый элемент исходной хэш-таблицы перемещается в новую выделенную путем вычисления значений хэша элементов с последующей операцией вставки. Перехэширование просто, но требует больших вычислительных затрат. ^{[40] : 478–479}

Альтернативы перефразированию всего сразу

Некоторые реализации хэш-таблиц, особенно в системах реального времени , не могут окупить цену увеличения хэш-таблицы сразу, поскольку это может прервать критические по времени операции. Если невозможно избежать динамического изменения размера, решением является постепенное изменение размера, чтобы избежать скачка хранилища — обычно на 50% от размера новой таблицы — во время повторного хэширования и избежать фрагментации памяти , которая запускает уплотнение кучи из-за освобождения больших блоков памяти, вызванного старой хэш-таблицей. ^{[41] : 2–3} В таком случае операция повторного хэширования выполняется постепенно путем расширения предыдущего блока памяти, выделенного для старой хэш-таблицы, таким образом, чтобы сегменты хэш-таблицы оставались неизменными. Обычный подход к амортизированному повторному хэшированию включает поддержание двух хэш-функций и . Процесс перехеширования элементов корзины в соответствии с новой хеш-функцией называется очисткой , которая реализуется с помощью шаблона команды путем инкапсуляции таких операций, как , и с помощью оболочки, так что каждый элемент в корзине перехешируется, а его процедура включает следующее: ^{[41] : 3} ${\displaystyle h_{\text{old}}}$ ${\displaystyle h_{\text{new}}}$ ${\displaystyle \mathrm {Add} (\mathrm {key} )}$ ${\displaystyle \mathrm {Get} (\mathrm {key} )}$ ${\displaystyle \mathrm {Delete} (\mathrm {key} )}$ ${\displaystyle \mathrm {Lookup} (\mathrm {key} ,{\text{command}})}$

• Чистое ведро. ${\displaystyle \mathrm {Table} [h_{\text{old}}(\mathrm {key} )]}$
• Чистое ведро. ${\displaystyle \mathrm {Table} [h_{\text{new}}(\mathrm {key} )]}$
• Команда выполняется .

Линейное хеширование

Линейное хеширование — это реализация хеш-таблицы, которая позволяет динамически увеличивать или уменьшать таблицу по одному блоку за раз. ^[42]

Производительность

Производительность хэш-таблицы зависит от способности хэш-функции генерировать квазислучайные числа ( ) для записей в хэш-таблице, где , а обозначает ключ, количество блоков и хэш-функцию, такую ​​что . Если хэш-функция генерирует то же самое для различных ключей ( ), это приводит к коллизии , которая решается различными способами. Постоянная временная сложность ( ) операции в хэш-таблице предполагается при условии, что хэш-функция не генерирует конфликтующие индексы; таким образом, производительность хэш-таблицы прямо пропорциональна способности выбранной хэш-функции рассеивать индексы. ^{[43] : 1} Однако построение такой хэш-функции практически неосуществимо , поэтому реализации зависят от методов разрешения коллизий , специфичных для конкретного случая, для достижения более высокой производительности. ^{[43] : 2} ${\displaystyle \sigma }$ ${\displaystyle K}$ ${\displaystyle n}$ ${\displaystyle h(x)}$ ${\displaystyle \sigma \ =\ h(K)\ \%\ n}$ ${\displaystyle \sigma }$ ${\displaystyle K_{1}\neq K_{2},\ h(K_{1})\ =\ h(K_{2})}$ ${\displaystyle O(1)}$

Приложения

Ассоциативные массивы

Хэш-таблицы обычно используются для реализации многих типов таблиц в памяти. Они используются для реализации ассоциативных массивов . ^[29]

Индексация базы данных

Хэш-таблицы также могут использоваться в качестве дисковых структур данных и индексов баз данных (например, в dbm ), хотя в этих приложениях более популярны B-деревья . ^[44]

Кэши

Хэш-таблицы могут использоваться для реализации кэшей , вспомогательных таблиц данных, которые используются для ускорения доступа к данным, которые в основном хранятся на более медленных носителях. В этом приложении хэш-коллизии могут быть обработаны путем отбрасывания одной из двух конфликтующих записей — обычно путем стирания старого элемента, который в данный момент хранится в таблице, и перезаписи его новым элементом, так что каждый элемент в таблице имеет уникальное хэш-значение. ^{[45] [46]}

Наборы

Хеш-таблицы могут использоваться при реализации структуры данных множеств , которая может хранить уникальные значения без какого-либо определенного порядка; множество обычно используется для проверки принадлежности значения к коллекции, а не для извлечения элемента. ^[47]

Таблица транспозиции

Таблица транспозиции в сложную хэш-таблицу, в которой хранится информация о каждом разделе, в котором производился поиск. ^[48]

Реализации

Многие языки программирования предоставляют функциональность хеш-таблиц либо в виде встроенных ассоциативных массивов, либо в виде стандартных библиотечных модулей.

В JavaScript «объект» — это изменяемая коллекция пар ключ-значение (называемых «свойствами»), где каждый ключ — это либо строка, либо гарантированно уникальный «символ»; любое другое значение, используемое в качестве ключа, сначала приводится к строке. Помимо семи «примитивных» типов данных, каждое значение в JavaScript является объектом. ^[49] ECMAScript 2015 также добавил Mapструктуру данных, которая принимает произвольные значения в качестве ключей. ^[50]

C++11 включает unordered_mapв свою стандартную библиотеку для хранения ключей и значений произвольных типов . ^[51]

Встроенная функция Gomap реализует хеш-таблицу в форме типа . [ ^52]

Язык программирования JavaHashSet включает в себя коллекции , HashMap, LinkedHashSet, и LinkedHashMap generic . ^[53]

Встроенная функция Pythondict реализует хеш-таблицу в виде типа . [ ^54]

Встроенная функция RubyHash использует модель открытой адресации, начиная с версии Ruby 2.4. ^[55]

Язык программирования RustHashMap включает в себя , HashSetкак часть стандартной библиотеки Rust. ^[56]

Стандартная библиотека .NETHashSet включает в себя и Dictionary, ^{[57] [58]} поэтому ее можно использовать из таких языков, как C# и VB.NET . ^[59]

Смотрите также

• Фильтр Блума
• Последовательное хеширование
• Распределенная хэш-таблица
• Расширяемое хеширование
• Массив хэшей, отображенный в виде trie-дерева
• Ленивое удаление
• хеширование Пирсона
• ФотоДНК
• Алгоритм поиска строки Рабина–Карпа
• Структура данных поиска
• Стабильное хеширование
• Краткая хэш-таблица

Ссылки

1. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009). Введение в алгоритмы (3-е изд.). Массачусетский технологический институт. стр. 253–280. ISBN  978-0-262-03384-8.
2. Мельхорн, Курт ; Сандерс, Питер (2008). "Хэш-таблицы и ассоциативные массивы" (PDF) . Алгоритмы и структуры данных . Springer. стр. 81–98. doi :10.1007/978-3-540-77978-0_4. ISBN 978-3-540-77977-3.
3. Лейзерсон, Чарльз Э. (осень 2005 г.). "Лекция 13: амортизированные алгоритмы, удвоение таблиц, метод потенциалов". курс MIT 6.046J/18.410J Введение в алгоритмы . Архивировано из оригинала 7 августа 2009 г.
4. Кнут, Дональд (1998). Искусство программирования . Том 3: Сортировка и поиск (2-е изд.). Addison-Wesley. С. 513–558. ISBN 978-0-201-89685-5.
5. Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л.; Стайн , Клиффорд (2001). «Глава 11: Хэш-таблицы». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. стр. 221–252. ISBN 978-0-262-53196-2.
6. Седжвик, Роберт ; Уэйн, Кевин (2011). Алгоритмы. Том 1 (4-е изд.). Addison-Wesley Professional – через Принстонский университет , кафедру компьютерных наук.
7. Konheim, Alan G. (2010). Хеширование в информатике . doi :10.1002/9780470630617. ISBN 978-0-470-34473-6.
8. Мехта, Динеш П.; Мехта, Динеш П.; Сахни, Сартай, ред. (2004). Справочник по структурам данных и приложениям . doi :10.1201/9781420035179. ISBN 978-0-429-14701-2.
9. Майерс, Эндрю (2008). «CS 312: Hash tables and amortized analysis». Корнелльский университет , кафедра компьютерных наук. Архивировано из оригинала 26 апреля 2021 г. Получено 26 октября 2021 г. – через cs.cornell.edu.
10. Джеймс С. Планк и Брэд Вандер Занден. «Конспект лекций CS140 — Хеширование».
11. Maurer, WD; Lewis, TG (март 1975). «Методы хэш-таблиц». ACM Computing Surveys . 7 (1): 5–19. doi :10.1145/356643.356645. S2CID  17874775.
12. Owolabi, Olumide (февраль 2003 г.). «Эмпирические исследования некоторых функций хеширования». Информационные и программные технологии . 45 (2): 109–112. doi :10.1016/S0950-5849(02)00174-X.
13. Lu, Yi; Prabhakar, Balaji; Bonomi, Flavio (2006). Perfect Hashing for Network Applications . 2006 IEEE International Symposium on Information Theory. стр. 2774–2778. doi :10.1109/ISIT.2006.261567. ISBN 1-4244-0505-X. S2CID  1494710.
14. Belazzougui, Djamal; Botelho, Fabiano C.; Dietzfelbinger, Martin (2009). "Hash, displace, and compress" (PDF) . Алгоритмы — ESA 2009: 17-й ежегодный европейский симпозиум, Копенгаген, Дания, 7–9 сентября 2009 г., Труды . Заметки лекций по информатике . Том 5757. Берлин: Springer. стр. 682–693. CiteSeerX 10.1.1.568.130 . doi :10.1007/978-3-642-04128-0_61. MR  2557794. 
15. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001). "Глава 11: Хэш-таблицы". Введение в алгоритмы (2-е изд.). Массачусетский технологический институт . ISBN 978-0-262-53196-2.
16. Пирсон, Карл (1900). «О критерии, согласно которому данная система отклонений от вероятной в случае коррелированной системы переменных такова, что можно обоснованно предположить, что она возникла из случайной выборки». Philosophical Magazine . Серия 5. 50 (302): 157–175. doi :10.1080/14786440009463897.
17. Плакетт, Робин (1983). «Карл Пирсон и критерий хи-квадрат». International Statistical Review . 51 (1): 59–72. doi :10.2307/1402731. JSTOR  1402731.
18. Wang, Thomas (март 1997). "Prime Double Hash Table". Архивировано из оригинала 3 сентября 1999 года . Получено 10 мая 2015 года .
19. Wegman, Mark N.; Carter, J.Lawrence (июнь 1981). «Новые хэш-функции и их использование в аутентификации и равенстве множеств». Журнал компьютерных и системных наук . 22 (3): 265–279. doi : 10.1016/0022-0000(81)90033-7 .
20. Дональд Э. Кнут (24 апреля 1998 г.). Искусство программирования: Том 3: Сортировка и поиск. Addison-Wesley Professional. ISBN 978-0-201-89685-5.
21. Демейн, Эрик; Линд, Джефф (весна 2003 г.). "Лекция 2" (PDF) . 6.897: Расширенные структуры данных. Лаборатория компьютерных наук и искусственного интеллекта Массачусетского технологического института . Архивировано (PDF) из оригинала 15 июня 2010 г. . Получено 30 июня 2008 г.
22. Culpepper, J. Shane; Moffat, Alistair (2005). "Enhanced Byte Codes with Restricted Prefix Properties". Обработка строк и извлечение информации . Конспект лекций по информатике. Том 3772. С. 1–12. doi :10.1007/11575832_1. ISBN 978-3-540-29740-6.
23. Уиллард, Дэн Э. (2000). «Исследование вычислительной геометрии, деревьев Ван Эмде Боаса и хеширования с точки зрения дерева слияния». SIAM Journal on Computing . 29 (3): 1030–1049. doi :10.1137/S0097539797322425. MR  1740562..
24. Аскитис, Николас; Синха, Ранджан (октябрь 2010 г.). «Разработка масштабируемых, кэширующих и пространственно-эффективных попыток для строк». Журнал VLDB . 19 (5): 633–660. doi :10.1007/s00778-010-0183-9.
25. Аскитис, Николас; Зобель, Джастин (октябрь 2005 г.). «Разрешение коллизий с учетом кэширования в строковых хэш-таблицах». Труды 12-й Международной конференции по обработке строк и поиску информации (SPIRE 2005) . Том 3772/2005. С. 91–102. doi :10.1007/11575832_11. ISBN 978-3-540-29740-6.
26. Аскитис, Николас (2009). "Быстрые и компактные хэш-таблицы для целочисленных ключей" (PDF) . Труды 32-й Австралазийской конференции по информатике (ACSC 2009) . Том 91. С. 113–122. ISBN 978-1-920682-72-9. Архивировано из оригинала (PDF) 16 февраля 2011 г. . Получено 13 июня 2010 г. .
27. Тененбаум, Аарон М.; Лангсам, Едидия; Аугенштейн, Моше Дж. (1990). Структуры данных с использованием C . Прентис Холл. стр. 456–461, с. 472. ИСБН 978-0-13-199746-2.
28. Паг, Расмус ; Родлер, Флемминг Фриш (2001). «Кукушка Хашинг». Алгоритмы — ЕКА 2001 . Конспекты лекций по информатике. Том. 2161. стр. 121–133. CiteSeerX 10.1.1.25.4189 . дои : 10.1007/3-540-44676-1_10. ISBN  978-3-540-42493-2.
29. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001), "11 хэш-таблиц", Введение в алгоритмы (2-е изд.), MIT Press и McGraw-Hill , стр. 221–252, ISBN 0-262-03293-7.
30. Vitter, Jeffery S.; Chen, Wen-Chin (1987). Разработка и анализ объединенного хеширования . Нью-Йорк, США: Oxford University Press . ISBN 978-0-19-504182-8– через Archive.org .
31. Паг, Расмус ; Родлер, Флемминг Фриш (2001). «Кукушка Хашинг». Алгоритмы — ЕКА 2001 . Конспекты лекций по информатике. Том. 2161. стр. 121–133. CiteSeerX 10.1.1.25.4189 . дои : 10.1007/3-540-44676-1_10. ISBN  978-3-540-42493-2.
32. Herlihy, Морис; Shavit, Нир; Tzafrir, Моран (2008). "Hopscotch Hashing". Распределенные вычисления . Конспект лекций по информатике. Том 5218. С. 350–364. doi :10.1007/978-3-540-87779-0_24. ISBN 978-3-540-87778-3.
33. Селис, Педро (1986). Хэширование Робин Гуда (PDF) . Онтарио, Канада: Университет Ватерлоо , факультет компьютерных наук. ISBN 978-0-315-29700-5. OCLC  14083698. Архивировано (PDF) из оригинала 1 ноября 2021 г. . Получено 2 ноября 2021 г. .
34. Poblete, PV; Viola, A. (июль 2019 г.). «Анализ алгоритмов Робина Гуда и других хеширования в рамках модели случайного зондирования с удалениями и без них». Комбинаторика, вероятность и вычисления . 28 (4): 600–617. doi :10.1017/S0963548318000408. S2CID  125374363.
35. Кларксон, Майкл (2014). «Лекция 13: Хэш-таблицы». Корнелльский университет , кафедра компьютерных наук. Архивировано из оригинала 7 октября 2021 г. Получено 1 ноября 2021 г. – через cs.cornell.edu.
36. Gries, David (2017). "JavaHyperText and Data Structure: Robin Hood Hashing" (PDF) . Корнелльский университет , Департамент компьютерных наук. Архивировано (PDF) из оригинала 26 апреля 2021 г. . Получено 2 ноября 2021 г. – через cs.cornell.edu.
37. Селис, Педро (28 марта 1988 г.). Внешнее хеширование Робина Гуда (PDF) (технический отчет). Блумингтон, Индиана: Университет Индианы , кафедра компьютерных наук. 246. Архивировано (PDF) из оригинала 3 ноября 2021 г. Получено 2 ноября 2021 г.
38. Goddard, Wayne (2021). "Глава C5: Хэш-таблицы" (PDF) . Clemson University . стр. 15–16 . Получено 4 декабря 2023 г. .
39. Девадас, Шрини; Демейн, Эрик (25 февраля 2011 г.). «Введение в алгоритмы: изменение размера хэш-таблиц» (PDF) . Массачусетский технологический институт , кафедра компьютерных наук. Архивировано (PDF) из оригинала 7 мая 2021 г. . Получено 9 ноября 2021 г. – через MIT OpenCourseWare .
40. Thareja, Reema (2014). «Хеширование и коллизия». Структуры данных с использованием C. Oxford University Press. С. 464–488. ISBN 978-0-19-809930-7.
41. Фридман, Скотт; Кришнан, Ананд; Лейдефрост, Николас (18 марта 2003 г.). "Хэш-таблицы для встраиваемых и систем реального времени" (PDF) . Все исследования в области компьютерных наук и техники . Вашингтонский университет в Сент-Луисе . doi :10.7936/K7WD3XXV. Архивировано (PDF) из оригинала 9 июня 2021 г. . Получено 9 ноября 2021 г. – через Северо-Западный университет , кафедра компьютерных наук.
42. Литвин, Витольд (1980). «Линейное хеширование: новый инструмент для адресации файлов и таблиц» (PDF) . Proc. 6th Conference on Very Large Databases . Carnegie Mellon University . pp. 212–223. Архивировано (PDF) из оригинала 6 мая 2021 г. . Получено 10 ноября 2021 г. – через cs.cmu.edu.
43. Dijk, Tom Van (2010). "Analysing and Improving Hash Table Performance" (PDF) . Нидерланды : Университет Твенте . Архивировано (PDF) из оригинала 6 ноября 2021 г. . Получено 31 декабря 2021 г. .
44. Лех Банаховский. «Индексы и внешняя сортировка». pl:Польско-Японская академия компьютерных технологий. Архивировано из оригинала 26 марта 2022 года . Проверено 26 марта 2022 г.
45. Чжун, Лян; Чжэн, Сюэцянь; Лю, Юн; Ван, Мэнтин; Цао, Ян (февраль 2020 г.). «Максимизация коэффициента попадания в кэш при коммуникациях между устройствами, наложенных на сотовые сети». China Communications . 17 (2): 232–238. doi :10.23919/jcc.2020.02.018. S2CID  212649328.
46. Bottommley, James (1 января 2004 г.). «Понимание кэширования». Linux Journal . Архивировано из оригинала 4 декабря 2020 г. Получено 16 апреля 2022 г.
47. Джилл Симан (2014). "Set & Hash Tables" (PDF) . Техасский государственный университет . Архивировано из оригинала 1 апреля 2022 г. . Получено 26 марта 2022 г. .{{cite web}}: CS1 maint: бот: исходный статус URL неизвестен ( ссылка )
48. "Transposition Table - Chessprogramming wiki". chessprogramming.org . Архивировано из оригинала 14 февраля 2021 г. . Получено 1 мая 2020 г. .
49. "Типы и структуры данных JavaScript - JavaScript | MDN". developer.mozilla.org . Получено 24 июля 2022 г. .
50. "Карта - JavaScript | MDN". developer.mozilla.org . 20 июня 2023 г. . Получено 15 июля 2023 г. .
51. "Язык программирования C++ - Техническая спецификация" (PDF) . Международная организация по стандартизации . стр. 812–813. Архивировано из оригинала (PDF) 21 января 2022 г. . Получено 8 февраля 2022 г. .
52. "Спецификация языка программирования Go". go.dev . Получено 1 января 2023 г. .
53. "Lesson: Implementations (The Java™ Tutorials > Collections)". docs.oracle.com . Архивировано из оригинала 18 января 2017 г. . Получено 27 апреля 2018 г. .
54. Чжан, Хуан; Цзя, Юньвэй (2020). «Оптимизация повторного хэширования Redis на основе машинного обучения». Журнал физики: Серия конференций . 1453 (1): 3. Bibcode : 2020JPhCS1453a2048Z. doi : 10.1088/1742-6596/1453/1/012048 . S2CID  215943738.
55. Jonan Scheffler (25 декабря 2016 г.). «Ruby 2.4 Released: Faster Hashes, Unified Integers and Better Rounding». heroku.com . Архивировано из оригинала 3 июля 2019 г. . Получено 3 июля 2019 г. .
56. "doc.rust-lang.org". Архивировано из оригинала 8 декабря 2022 г. Получено 14 декабря 2022 г.
57. "HashSet Class (System.Collections.Generic)". learn.microsoft.com . Получено 1 июля 2023 г. .
58. dotnet-bot. "Класс словаря (System.Collections.Generic)". learn.microsoft.com . Получено 16 января 2024 г. .
59. "Пример VB.NET HashSet". Dot Net Perls .

Дальнейшее чтение

• Tamassia, Roberto; Goodrich, Michael T. (2006). "Глава девятая: Карты и словари". Структуры данных и алгоритмы в Java : [обновлено для Java 5.0] (4-е изд.). Hoboken, NJ: Wiley. стр. 369–418. ISBN 978-0-471-73884-8.
• McKenzie, BJ; Harries, R.; Bell, T. (февраль 1990 г.). «Выбор алгоритма хеширования». Software: Practice and Experience . 20 (2): 209–224. doi :10.1002/spe.4380200207. hdl : 10092/9691 . S2CID  12854386.

Внешние ссылки

• Запись NIST о хэш-таблицах
• Открытые структуры данных – Глава 5 – Хеш-таблицы, Пэт Морин
• Введение в алгоритмы MIT: Хеширование 1 Видеолекция MIT OCW
• Введение в алгоритмы MIT: Хеширование 2 Видеолекция MIT OCW