Частичная корреляция

Понятие в теории вероятностей и статистике

В теории вероятностей и статистике частичная корреляция измеряет степень связи между двумя случайными величинами , при этом влияние набора контролирующих случайных величин удалено. При определении числовой связи между двумя интересующими переменными использование их коэффициента корреляции даст вводящие в заблуждение результаты , если есть другая смешивающая переменная , которая численно связана с обеими интересующими переменными. Эту вводящую в заблуждение информацию можно избежать, контролируя смешивающую переменную, что делается путем вычисления частичного коэффициента корреляции. Именно это и является мотивацией для включения других переменных правой стороны в множественную регрессию ; но хотя множественная регрессия дает непредвзятые результаты для размера эффекта , она не дает числового значения меры силы связи между двумя интересующими переменными.

Например, учитывая экономические данные о потреблении, доходе и богатстве различных людей, рассмотрим взаимосвязь между потреблением и доходом. Неспособность контролировать богатство при вычислении коэффициента корреляции между потреблением и доходом даст вводящий в заблуждение результат, поскольку доход может быть численно связан с богатством, которое, в свою очередь, может быть численно связано с потреблением; измеренная корреляция между потреблением и доходом может фактически быть загрязнена этими другими корреляциями. Использование частичной корреляции позволяет избежать этой проблемы.

Как и коэффициент корреляции, коэффициент частной корреляции принимает значение в диапазоне от –1 до 1. Значение –1 передает идеальную отрицательную корреляцию, контролирующую некоторые переменные (то есть точную линейную связь, в которой более высокие значения одной переменной связаны с более низкими значениями другой); значение 1 передает идеальную положительную линейную связь, а значение 0 сообщает об отсутствии линейной связи.

Частная корреляция совпадает с условной корреляцией , если случайные величины совместно распределены как многомерное нормальное , другое эллиптическое , многомерное гипергеометрическое , многомерное отрицательное гипергеометрическое , полиномиальное или распределение Дирихле , но не в общем случае. ^[1]

Формальное определение

Формально, частная корреляция между X и Y при заданном наборе n управляющих переменных Z = { Z ₁ , Z ₂ , ..., Z n }, записанная как ρ XY · Z , является корреляцией между остатками e X и e Y , полученными в результате линейной регрессии X с _Z и Y _{с Z ,} соответственно . Частная корреляция первого _{порядка} ( т _. е . когда n = 1 ) является разницей между корреляцией и произведением устранимых корреляций, деленной на произведение коэффициентов отчуждения устранимых корреляций. Коэффициент отчуждения и его связь с совместной дисперсией через корреляцию доступны в Guilford (1973, стр. 344–345). ^[2]

Вычисление

Использование линейной регрессии

Простой способ вычисления выборочной частной корреляции для некоторых данных — решить две связанные задачи линейной регрессии и вычислить корреляцию между остатками. Пусть X и Y — случайные величины, принимающие действительные значения, а Z — n -мерная векторная случайная величина. Пусть x _i , y _i и z _i обозначают i -е из наблюдений iid из некоторого совместного распределения вероятностей над действительными случайными величинами X , Y , и Z , причем z _i было дополнено на 1, чтобы разрешить постоянный член в регрессии. Решение задачи линейной регрессии сводится к нахождению ( n +1)-мерных векторов коэффициентов регрессии и таких, что ${\displaystyle N}$ ${\displaystyle \mathbf {w} _{X}^{*}}$ ${\displaystyle \mathbf {w} _{Y}^{*}}$

${\displaystyle \mathbf {w} _{X}^{*}=\arg \min _{\mathbf {w} }\left\{\sum _{i=1}^{N}(x_{i}-\langle \mathbf {w} ,\mathbf {z} _{i}\rangle )^{2}\right\}}$

${\displaystyle \mathbf {w} _{Y}^{*}=\arg \min _{\mathbf {w} }\left\{\sum _{i=1}^{N}(y_{i}-\langle \mathbf {w} ,\mathbf {z} _{i}\rangle )^{2}\right\}}$

где — число наблюдений, а — скалярное произведение векторов и . ${\displaystyle N}$ ${\displaystyle \langle \mathbf {w} ,\mathbf {z} _{i}\rangle }$ ${\displaystyle \mathbf {w} }$ ${\displaystyle \mathbf {z} _{i}}$

Остатки тогда

${\displaystyle e_{X,i}=x_{i}-\langle \mathbf {w} _{X}^{*},\mathbf {z} _{i}\rangle }$

${\displaystyle e_{Y,i}=y_{i}-\langle \mathbf {w} _{Y}^{*},\mathbf {z} _{i}\rangle }$

и тогда выборочная частная корреляция определяется по обычной формуле для выборочной корреляции , но между этими новыми полученными значениями:

${\displaystyle {\begin{aligned}{\hat {\rho }}_{XY\cdot \mathbf {Z} }&={\frac {N\sum _{i=1}^{N}e_{X,i}e_{Y,i}-\sum _{i=1}^{N}e_{X,i}\sum _{i=1}^{N}e_{Y,i}}{{\sqrt {N\sum _{i=1}^{N}e_{X,i}^{2}-\left(\sum _{i=1}^{N}e_{X,i}\right)^{2}}}~{\sqrt {N\sum _{i=1}^{N}e_{Y,i}^{2}-\left(\sum _{i=1}^{N}e_{Y,i}\right)^{2}}}}}\\&={\frac {N\sum _{i=1}^{N}e_{X,i}e_{Y,i}}{{\sqrt {N\sum _{i=1}^{N}e_{X,i}^{2}}}~{\sqrt {N\sum _{i=1}^{N}e_{Y,i}^{2}}}}}.\end{aligned}}}$

В первом выражении все три члена после знака минус равны 0, поскольку каждый из них содержит сумму остатков от обычной регрессии наименьших квадратов .

Пример

Рассмотрим следующие данные по трем переменным X , Y и Z :

Вычисление коэффициента корреляции Пирсона между переменными X и Y дает приблизительно 0,970, тогда как вычисление частной корреляции между X и Y с использованием приведенной выше формулы дает частичную корреляцию 0,919. Вычисления были выполнены с использованием R со следующим кодом.

> X <- c ( 2 , 4 , 15 , 20 ) > Y <- c ( 1 , 2 , 3 , 4 ) > Z <- c ( 0 , 0 , 1 , 1 ) > mm1 <- lm ( X ~ Z ) > res1 <- мм1 $ остатки > мм2 <- lm ( Y ~ Z ) > res2 <- мм2 $ остатки > cor ( res1 , res2 ) [1] 0,919145 > cor ( X , Y ) [1] 0,9695016 > GeneralCorr :: parcorMany ( cbind ( X , Y , Z ))  nami namj partij partji rijMrji [1,] "X" "Y" "0,8844" "1" "-0,1156" [2,] "X" "Z" "0,1581" "1" "-0,8419"               

Нижняя часть кода выше сообщает, что обобщенный нелинейный частный коэффициент корреляции между X и Y после удаления нелинейного эффекта Z равен 0,8844. Кроме того, обобщенный нелинейный частный коэффициент корреляции между X и Z после удаления нелинейного эффекта Y равен 0,1581. Подробности см. в пакете R `generalCorr' и его виньетках. Моделирование и другие подробности см. в Vinod (2017) "Generalized Correlation and kernel causality with applications in development economics," Communications in Statistics - Simulation and Computation, vol. 46, [4513, 4534], доступно онлайн: 29 декабря 2015 г., URL https://doi.org/10.1080/03610918.2015.1122048.

Использование рекурсивной формулы

Решение задач линейной регрессии может быть вычислительно затратным. На самом деле, частная корреляция n -го порядка (т.е. с | Z | = n ) может быть легко вычислена из трех частных корреляций ( n - 1)-го порядка. Частная корреляция нулевого порядка ρ _{XY ·Ø} определяется как регулярный коэффициент корреляции ρ _XY .

Это справедливо для любого, что ^[3] ${\displaystyle Z_{0}\in \mathbf {Z} ,}$

${\displaystyle \rho _{XY\cdot \mathbf {Z} }={\frac {\rho _{XY\cdot \mathbf {Z} \setminus \{Z_{0}\}}-\rho _{XZ_{0}\cdot \mathbf {Z} \setminus \{Z_{0}\}}\rho _{Z_{0}Y\cdot \mathbf {Z} \setminus \{Z_{0}\}}}{{\sqrt {1-\rho _{XZ_{0}\cdot \mathbf {Z} \setminus \{Z_{0}\}}^{2}}}{\sqrt {1-\rho _{Z_{0}Y\cdot \mathbf {Z} \setminus \{Z_{0}\}}^{2}}}}}}$

Наивная реализация этого вычисления как рекурсивного алгоритма дает экспоненциальную временную сложность . Однако это вычисление имеет свойство перекрывающихся подзадач , так что использование динамического программирования или простое кэширование результатов рекурсивных вызовов дает сложность . ${\displaystyle {\mathcal {O}}(n^{3})}$

Обратите внимание, что в случае, когда Z — единственная переменная, это сводится к: ^{[ необходима ссылка ]}

${\displaystyle \rho _{XY\cdot Z}={\frac {\rho _{XY}-\rho _{XZ}\rho _{ZY}}{{\sqrt {1-\rho _{XZ}^{2}}}{\sqrt {1-\rho _{ZY}^{2}}}}}}$

Использование инверсии матрицы

Частичная корреляция также может быть записана в терминах матрицы совместной точности. Рассмотрим набор случайных величин мощности n . Мы хотим получить частичную корреляцию между двумя переменными и при всех остальных, т. е . . Предположим, что (совместная/полная) ковариационная матрица положительно определена и , следовательно, обратима . Если матрица точности определена как , то ${\displaystyle \mathbf {V} ={X_{1},\dots ,X_{n}}}$ ${\displaystyle X_{i}}$ ${\displaystyle X_{j}}$ ${\displaystyle \mathbf {V} \setminus \{X_{i},X_{j}\}}$ ${\displaystyle \Sigma =(\sigma _{ij})}$ ${\displaystyle \Omega =(p_{ij})=\Sigma ^{-1}}$

Для вычисления этого требуется , обратная матрица ковариации , которая выполняется во времени (используя выборочную ковариационную матрицу для получения выборочной частичной корреляции). Обратите внимание, что требуется только одна инверсия матрицы, чтобы получить все частичные корреляции между парами переменных в . ${\displaystyle \Sigma ^{-1}}$ ${\displaystyle \Sigma }$ ${\displaystyle {\mathcal {O}}(n^{3})}$ ${\displaystyle \mathbf {V} }$

Чтобы доказать уравнение ( 1 ), вернитесь к предыдущей записи (т.е. ) и начните с определения частичной корреляции: ρ _{XY · Z} — это корреляция между остатками e _X и e _{Y ,} полученными в результате линейной регрессии X с Z и Y с Z соответственно. ${\displaystyle X,Y,\mathbf {Z} \leftrightarrow X_{i},X_{j},\mathbf {V} \setminus \{X_{i},X_{j}\}}$

Во-первых, предположим, что являются коэффициентами для линейной регрессии, то есть, ${\displaystyle \beta ,\gamma }$

${\displaystyle \beta =\operatorname {argmin} _{\beta }\mathbb {E} \|X-\beta ^{T}Z\|^{2}}$

${\displaystyle \gamma =\operatorname {argmin} _{\gamma }\mathbb {E} \|Y-\gamma ^{T}Z\|^{2}}$

Запишите совместную ковариационную матрицу для вектора как ${\displaystyle (X,Y,Z^{T})^{T}}$

${\displaystyle \Sigma ={\begin{bmatrix}\Sigma _{XX}&\Sigma _{XY}&\Sigma _{XZ}\\\Sigma _{YX}&\Sigma _{YY}&\Sigma _{YZ}\\\Sigma _{ZX}&\Sigma _{ZY}&\Sigma _{ZZ}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\\\end{bmatrix}}}$

где Тогда стандартная формула линейной регрессии дает $${\displaystyle C_{11}={\begin{bmatrix}\Sigma _{XX}&\Sigma _{XY}\\\Sigma _{YX}&\Sigma _{YY}\end{bmatrix}},\qquad C_{12}={\begin{bmatrix}\Sigma _{XZ}\\\Sigma _{YZ}\end{bmatrix}},\qquad C_{21}={\begin{bmatrix}\Sigma _{ZX}&\Sigma _{ZY}\end{bmatrix}},\qquad C_{22}=\Sigma _{ZZ}}$$

${\displaystyle \beta =\left(\Sigma _{ZZ}\right)^{-1}\Sigma _{ZX}}$

Следовательно, остатки можно записать как

${\displaystyle R_{X}=X-\beta ^{T}Z=X-\Sigma _{XZ}\left(\Sigma _{ZZ}\right)^{-1}Z}$

Обратите внимание, что имеет нулевое ожидание из-за включения члена-перехвата в . Вычисление ковариации теперь дает ${\displaystyle R_{X}}$ ${\displaystyle Z}$

Далее запишем матрицу точности в аналогичной блочной форме: ${\displaystyle \Omega =\Sigma ^{-1}}$

${\displaystyle \Omega ={\begin{bmatrix}\Omega _{XX}&\Omega _{XY}&\Omega _{XZ}\\\Omega _{YX}&\Omega _{YY}&\Omega _{YZ}\\\Omega _{ZX}&\Omega _{ZY}&\Omega _{ZZ}\end{bmatrix}}={\begin{bmatrix}P_{11}&P_{12}\\P_{21}&P_{22}\\\end{bmatrix}}}$

Тогда, по формуле Шура для блочно-матричного обращения ,

${\displaystyle P_{11}^{-1}=C_{11}-C_{12}C_{22}^{-1}C_{21}}$

Элементы матрицы с правой стороны — это в точности ковариации, ранее вычисленные в ( 2 ), что дает

${\displaystyle P_{11}^{-1}={\begin{bmatrix}\operatorname {Cov} (R_{X},R_{X})&\operatorname {Cov} (R_{X},R_{Y})\\\operatorname {Cov} (R_{Y},R_{X})&\operatorname {Cov} (R_{Y},R_{Y})\\\end{bmatrix}}}$

Использование формулы для обратной матрицы 2×2 дает

${\displaystyle {\begin{aligned}P_{11}^{-1}&={\frac {1}{{\text{det}}P_{11}}}{\begin{pmatrix}[P_{11}]_{22}&-[P_{11}]_{12}\\-[P_{11}]_{21}&[P_{11}]_{11}\\\end{pmatrix}}\\&={\frac {1}{{\text{det}}P_{11}}}{\begin{pmatrix}p_{YY}&-p_{XY}\\-p_{YX}&p_{XX}\\\end{pmatrix}}\end{aligned}}}$

Итак, действительно, частичная корреляция

${\displaystyle \rho _{XY\cdot Z}={\frac {\operatorname {Cov} (R_{X},R_{Y})}{\sqrt {\operatorname {Cov} (R_{X},R_{X})\operatorname {Cov} (R_{Y},R_{Y})}}}={\frac {-{\tfrac {1}{{\text{det}}P_{11}}}p_{XY}}{\sqrt {{\tfrac {1}{{\text{det}}P_{11}}}p_{XX}{\tfrac {1}{{\text{det}}P_{11}}}p_{YY}}}}=-{\frac {p_{XY}}{\sqrt {p_{XX}p_{YY}}}}}$

как утверждается в ( 1 ).

Интерпретация

Геометрическая интерпретация частичной корреляции для случая N = 3 наблюдений и, следовательно, двумерной гиперплоскости

Геометрический

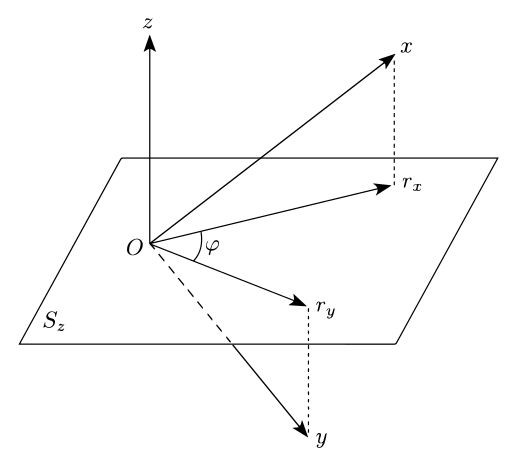
Пусть три переменные X , Y , Z (где Z — «контрольная» или «дополнительная переменная») выбраны из совместного распределения вероятностей по n переменным V. Далее, пусть v _i , 1 ≤ i ≤ N , будут N n -мерными iid наблюдениями, взятыми из совместного распределения вероятностей по V . Геометрическая интерпретация происходит из рассмотрения N -мерных векторов x (образованных последовательными значениями X по наблюдениям), y (образованных значениями Y ) и z (образованных значениями Z ).

Можно показать, что остатки e _X,i, возникающие из линейной регрессии X на Z , если их также рассматривать как N -мерный вектор e _X (обозначенный r _X в сопроводительном графике), имеют нулевое скалярное произведение с вектором z, порожденным Z. Это означает, что вектор остатков лежит на ( N –1)-мерной гиперплоскости S _z , которая перпендикулярна z .

То же самое относится и к остаткам e _Y,i, генерирующим вектор e _Y . Тогда искомая частная корреляция — это косинус угла φ между проекциями e _X и e _Y точек x и y , соответственно, на гиперплоскость, перпендикулярную z . ^{[4] : гл. 7}

Как условный тест независимости

При предположении, что все вовлеченные переменные являются многомерными гауссовыми , частная корреляция ρ _{XY · Z} равна нулю тогда и только тогда, когда X условно независим от Y при заданном Z. ^[1] Это свойство не выполняется в общем случае .

Чтобы проверить , подразумевает ли выборочная частная корреляция , что истинная частная корреляция популяции отличается от 0, можно использовать z-преобразование Фишера частной корреляции : ${\displaystyle {\hat {\rho }}_{XY\cdot \mathbf {Z} }}$

${\displaystyle z({\hat {\rho }}_{XY\cdot \mathbf {Z} })={\frac {1}{2}}\ln \left({\frac {1+{\hat {\rho }}_{XY\cdot \mathbf {Z} }}{1-{\hat {\rho }}_{XY\cdot \mathbf {Z} }}}\right)}$

Нулевая гипотеза должна быть проверена против альтернативы с двумя хвостами . может быть отклонена, если ${\displaystyle H_{0}:\rho _{XY\cdot \mathbf {Z} }=0}$ ${\displaystyle H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0}$ ${\displaystyle H_{0}}$

${\displaystyle {\sqrt {N-|\mathbf {Z} |-3}}\cdot |z({\hat {\rho }}_{XY\cdot \mathbf {Z} })|>\Phi ^{-1}(1-\alpha /2)}$

где — кумулятивная функция распределения Гаусса с нулевым средним и единичным стандартным отклонением , — уровень значимости , а — размер выборки . Это z -преобразование является приблизительным, и фактическое распределение выборочного (частного) коэффициента корреляции не является простым. Однако доступен точный t-тест, основанный на комбинации частного коэффициента регрессии, частного коэффициента корреляции и частных дисперсий. ^[5] ${\displaystyle \Phi }$ ${\displaystyle \alpha }$ ${\displaystyle H_{0}}$ ${\displaystyle N}$

Распределение выборочной частичной корреляции было описано Фишером. ^[6]

Получастичная корреляция (частичная корреляция)

Статистика получастичной (или частичной) корреляции похожа на статистику частичной корреляции; обе сравнивают вариации двух переменных после того, как определенные факторы контролируются. Однако для вычисления получастичной корреляции третья переменная сохраняется постоянной либо для X, либо для Y , но не для обоих; тогда как для частичной корреляции третья переменная сохраняется постоянной для обоих. ^[7] Получастичная корреляция сравнивает уникальную вариацию одной переменной (удалив вариацию, связанную с переменной(ыми) Z )) с неотфильтрованной вариацией другой, в то время как частичная корреляция сравнивает уникальную вариацию одной переменной с уникальной вариацией другой.

Получастную корреляцию можно рассматривать как более значимую с практической точки зрения, «потому что она масштабируется по отношению к (т.е. относительно) общей изменчивости зависимой (ответной) переменной». ^[8] И наоборот, она менее полезна с теоретической точки зрения, поскольку она менее точна в отношении роли уникального вклада независимой переменной.

Абсолютное значение получастной корреляции X с Y всегда меньше или равно значению частичной корреляции X с Y . Причина в следующем: предположим, что корреляция X с Z была удалена из X , что дало остаточный вектор e _x . При вычислении получастной корреляции Y по-прежнему содержит как уникальную дисперсию, так и дисперсию из-за ее связи с Z . Но e _x , будучи некоррелированным с Z , может объяснить только часть уникальной части дисперсии Y , а не часть, связанную с Z . Напротив, при частичной корреляции необходимо объяснить только e _y (часть дисперсии Y , которая не связана с Z ), поэтому дисперсии того типа, которую e _x не может объяснить , меньше .

Использование в анализе временных рядов

В анализе временных рядов частная автокорреляционная функция ( иногда «частичная корреляционная функция») временного ряда определяется для лага как ^{[ необходима ссылка ]} ${\displaystyle h}$

${\displaystyle \varphi (h)=\rho _{X_{0}X_{h}\,\cdot \,\{X_{1},\,\dots \,,X_{h-1}\}}}$

Эта функция используется для определения подходящей длины лага для авторегрессии .

Смотрите также

• Линейная регрессия
• Условная независимость
• Множественная корреляция
• Частичная декомпозиция информации

Ссылки

1. Баба, Кунихиро; Ритеи Сибата; Масааки Сибуя (2004). «Частичная корреляция и условная корреляция как меры условной независимости». Статистический журнал Австралии и Новой Зеландии . 46 (4): 657–664. дои : 10.1111/j.1467-842X.2004.00360.x. S2CID  123130024.
2. Гилфорд Дж. П., Фрухтер Б. (1973). Фундаментальная статистика в психологии и образовании . Токио: McGraw-Hill Kogakusha, LTD.
3. Ким, Сонхо (ноябрь 2015 г.). «ppcor: Пакет R для быстрого расчета коэффициентов получастичной корреляции». Communications for Statistical Applications and Methods . 22 (6): 665–674. doi :10.5351/CSAM.2015.22.6.665. ISSN  2287-7843. PMC 4681537. PMID 26688802  . 
4. Раммель, Р. Дж. (1976). «Понимание корреляции».
5. Кендалл МГ, Стюарт А. (1973) Продвинутая теория статистики , том 2 (3-е издание), ISBN 0-85264-215-6 , раздел 27.22 
6. Фишер, РА (1924). «Распределение частного коэффициента корреляции». Metron . 3 (3–4): 329–332.
7. "Частичная и получастичная корреляция". Архивировано из оригинала 6 февраля 2014 года.
8. StatSoft, Inc. (2010). «Получастичная (или частичная) корреляция», Электронный учебник статистики. Талса, Оклахома: StatSoft, доступ 15 января 2011 г.

Внешние ссылки

• Прохоров, А.В. (2001) [1994], "Частный коэффициент корреляции", Энциклопедия математики , Издательство EMS
• Математические формулы в разделе «Описание» процедуры PCORR библиотеки IMSL Numerical Library
• Пример с тремя переменными