Корреляция

Статистическая концепция

Несколько наборов точек ( x ,  y ) с коэффициентом корреляции Пирсона x и y для каждого набора. Корреляция отражает зашумленность и направление линейной зависимости (верхний ряд), но не наклон этой зависимости (средний) и многие аспекты нелинейных связей (нижний). Примечание: фигура в центре имеет наклон 0, но в этом случае коэффициент корреляции не определен, поскольку дисперсия Y равна нулю.

В статистике корреляция или зависимость — это любая статистическая связь, причинно - следственная или нет, между двумя случайными величинами или двумерными данными . Хотя в самом широком смысле «корреляция» может указывать на любой тип связи, в статистике она обычно относится к степени линейной связи пары переменных . Знакомые примеры зависимых явлений включают корреляцию между ростом родителей и их потомства, а также корреляцию между ценой товара и количеством, которое потребители готовы купить, как это изображено на так называемой кривой спроса .

Корреляции полезны, поскольку они могут указывать на прогностическую взаимосвязь, которую можно использовать на практике. Например, электроэнергетическая компания может производить меньше электроэнергии в мягкий день в зависимости от корреляции между спросом на электроэнергию и погодой. В этом примере существует причинно-следственная связь , поскольку экстремальные погодные условия заставляют людей использовать больше электроэнергии для отопления или охлаждения. Однако, как правило, наличия корреляции недостаточно для вывода о наличии причинно-следственной связи (т. е. корреляция не подразумевает причинно-следственную связь ).

Формально случайные величины являются зависимыми , если они не удовлетворяют математическому свойству вероятностной независимости . На неформальном языке корреляция является синонимом зависимости . Однако в техническом смысле корреляция относится к любому из нескольких конкретных типов математических операций между тестируемыми переменными и их соответствующими ожидаемыми значениями . По сути, корреляция — это мера того, как две или более переменных связаны друг с другом. Существует несколько коэффициентов корреляции , часто обозначаемых или , измеряющих степень корреляции. Наиболее распространенным из них является коэффициент корреляции Пирсона , который чувствителен только к линейной зависимости между двумя переменными (которая может присутствовать, даже если одна переменная является нелинейной функцией другой). Другие коэффициенты корреляции, такие как ранговая корреляция Спирмена , были разработаны как более надежные , чем коэффициент Пирсона, то есть более чувствительные к нелинейным взаимосвязям. ^{[1] [2] [3]} Взаимная информация также может применяться для измерения зависимости между двумя переменными. ${\displaystyle \rho }$ ${\displaystyle r}$

Коэффициент момента произведения Пирсона

Примеры диаграмм рассеяния различных наборов данных с различными коэффициентами корреляции.

Наиболее известной мерой зависимости между двумя величинами является коэффициент корреляции момента произведения Пирсона (PPMCC), или «коэффициент корреляции Пирсона», обычно называемый просто «коэффициентом корреляции». Он получается путем взятия отношения ковариации двух рассматриваемых переменных нашего набора числовых данных, нормализованного на квадратный корень их дисперсий. Математически ковариацию двух переменных просто делят на произведение их стандартных отклонений . Карл Пирсон разработал этот коэффициент на основе аналогичной, но несколько иной идеи Фрэнсиса Гальтона . ^[4]

Коэффициент корреляции момента продукта Пирсона пытается установить линию наилучшего соответствия для набора данных из двух переменных, по сути, распределяя ожидаемые значения, а результирующий коэффициент корреляции Пирсона показывает, насколько далеко фактический набор данных находится от ожидаемых значений. В зависимости от знака нашего коэффициента корреляции Пирсона мы можем получить либо отрицательную, либо положительную корреляцию, если между переменными нашего набора данных существует какая-либо связь. ^{[ нужна цитата ]}

Коэффициент корреляции населения между двумя случайными величинами , ожидаемыми значениями и стандартными отклонениями определяется как : ${\displaystyle \rho _{X,Y}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \mu _{X}}$ ${\displaystyle \mu _{Y}}$ ${\displaystyle \sigma _{X}}$ ${\displaystyle \sigma _{Y}}$

$${\displaystyle \rho _{X,Y}=\operatorname {corr} (X,Y)={\operatorname {cov} (X,Y) \over \sigma _{X}\sigma _{Y}}={\operatorname {E} [(X-\mu _{X})(Y-\mu _{Y})] \over \sigma _{X}\sigma _{Y}},\quad {\text{if}}\ \sigma _{X}\sigma _{Y}>0.}$$

где – оператор ожидаемого значения , означает ковариацию и является широко используемым альтернативным обозначением коэффициента корреляции. Корреляция Пирсона определяется только в том случае, если оба стандартных отклонения конечны и положительны. Альтернативная формула, выраженная исключительно в моментах : ${\displaystyle \operatorname {E} }$ ${\displaystyle \operatorname {cov} }$ ${\displaystyle \operatorname {corr} }$

$${\displaystyle \rho _{X,Y}={\operatorname {E} (XY)-\operatorname {E} (X)\operatorname {E} (Y) \over {\sqrt {\operatorname {E} (X^{2})-\operatorname {E} (X)^{2}}}\cdot {\sqrt {\operatorname {E} (Y^{2})-\operatorname {E} (Y)^{2}}}}}$$

Корреляция и независимость

Следствием неравенства Коши – Шварца является то, что абсолютное значение коэффициента корреляции Пирсона не превышает 1. Следовательно, значение коэффициента корреляции колеблется от -1 до +1. Коэффициент корреляции равен +1 в случае идеальной прямой (возрастающей) линейной зависимости (корреляции), -1 в случае совершенной обратной (убывающей) линейной зависимости ( антикорреляции ), ^[5] и некоторому значению в открытый интервал во всех остальных случаях, указывающий на степень линейной зависимости между переменными. По мере приближения к нулю взаимосвязь становится меньше (ближе к некоррелированной). Чем ближе коэффициент к –1 или 1, тем сильнее корреляция между переменными. ${\displaystyle (-1,1)}$

Если переменные независимы , коэффициент корреляции Пирсона равен 0, но обратное неверно, поскольку коэффициент корреляции обнаруживает только линейные зависимости между двумя переменными. Проще говоря, если две случайные величины X и Y независимы, то они некоррелированы, но если две случайные величины некоррелированы, то они могут быть, а могут и не быть независимыми.

$${\displaystyle {\begin{aligned}X,Y{\text{ independent}}\quad &\Rightarrow \quad \rho _{X,Y}=0\quad (X,Y{\text{ uncorrelated}})\\\rho _{X,Y}=0\quad (X,Y{\text{ uncorrelated}})\quad &\nRightarrow \quad X,Y{\text{ independent}}\end{aligned}}}$$

Например, предположим, что случайная величина симметрично распределена относительно нуля и . Тогда полностью определяется , так что и совершенно зависимы, но их корреляция равна нулю; они некоррелированы . Однако в частном случае, когда и совместно нормальны , некоррелированность эквивалентна независимости. ${\displaystyle X}$ ${\displaystyle Y=X^{2}}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$

Несмотря на то, что некоррелированные данные не обязательно подразумевают независимость, можно проверить, являются ли случайные величины независимыми, если их взаимная информация равна 0.

Выборочный коэффициент корреляции

Учитывая серию измерений пары, индексированной , выборочный коэффициент корреляции можно использовать для оценки популяционной корреляции Пирсона между и . Выборочный коэффициент корреляции определяется как ${\displaystyle n}$ ${\displaystyle (X_{i},Y_{i})}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle \rho _{X,Y}}$ ${\displaystyle X}$ ${\displaystyle Y}$

${\displaystyle r_{xy}\quad {\overset {\underset {\mathrm {def} }{}}{=}}\quad {\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{(n-1)s_{x}s_{y}}}={\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sqrt {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}\sum \limits _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}},}$

где и являются выборочными средними значениями и , и являются скорректированными выборочными стандартными отклонениями и . ${\displaystyle {\overline {x}}}$ ${\displaystyle {\overline {y}}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle s_{x}}$ ${\displaystyle s_{y}}$ ${\displaystyle X}$ ${\displaystyle Y}$

Эквивалентные выражения для ${\displaystyle r_{xy}}$

${\displaystyle {\begin{aligned}r_{xy}&={\frac {\sum x_{i}y_{i}-n{\bar {x}}{\bar {y}}}{ns'_{x}s'_{y}}}\\[5pt]&={\frac {n\sum x_{i}y_{i}-\sum x_{i}\sum y_{i}}{{\sqrt {n\sum x_{i}^{2}-(\sum x_{i})^{2}}}~{\sqrt {n\sum y_{i}^{2}-(\sum y_{i})^{2}}}}}.\end{aligned}}}$

где и – нескорректированные выборочные стандартные отклонения и . ${\displaystyle s'_{x}}$ ${\displaystyle s'_{y}}$ ${\displaystyle X}$ ${\displaystyle Y}$

Если и являются результатами измерений, которые содержат ошибку измерения, реалистичные пределы коэффициента корреляции составляют не от -1 до +1, а меньший диапазон. ^[6] Для случая линейной модели с одной независимой переменной коэффициент детерминации (R в квадрате) равен квадрату коэффициента момента произведения Пирсона. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle r_{xy}}$

Пример

Рассмотрим совместное распределение вероятностей X и Y , приведенное в таблице ниже.

Для этого совместного распределения предельные распределения таковы:

${\displaystyle \mathrm {P} (X=x)={\begin{cases}{\frac {1}{3}}&\quad {\text{for }}x=0\\{\frac {2}{3}}&\quad {\text{for }}x=1\end{cases}}}$

${\displaystyle \mathrm {P} (Y=y)={\begin{cases}{\frac {1}{3}}&\quad {\text{for }}y=-1\\{\frac {1}{3}}&\quad {\text{for }}y=0\\{\frac {1}{3}}&\quad {\text{for }}y=1\end{cases}}}$

Это дает следующие ожидания и отклонения:

${\displaystyle \mu _{X}={\frac {2}{3}}}$

${\displaystyle \mu _{Y}=0}$

${\displaystyle \sigma _{X}^{2}={\frac {2}{9}}}$

${\displaystyle \sigma _{Y}^{2}={\frac {2}{3}}}$

Поэтому:

${\displaystyle {\begin{aligned}\rho _{X,Y}&={\frac {1}{\sigma _{X}\sigma _{Y}}}\mathrm {E} [(X-\mu _{X})(Y-\mu _{Y})]\\[5pt]&={\frac {1}{\sigma _{X}\sigma _{Y}}}\sum _{x,y}{(x-\mu _{X})(y-\mu _{Y})\mathrm {P} (X=x,Y=y)}\\[5pt]&=\left(1-{\frac {2}{3}}\right)(-1-0){\frac {1}{3}}+\left(0-{\frac {2}{3}}\right)(0-0){\frac {1}{3}}+\left(1-{\frac {2}{3}}\right)(1-0){\frac {1}{3}}=0.\end{aligned}}}$

Коэффициенты ранговой корреляции

Коэффициенты ранговой корреляции , такие как коэффициент ранговой корреляции Спирмена и коэффициент ранговой корреляции Кендалла (τ), измеряют степень, в которой по мере увеличения одной переменной другая переменная имеет тенденцию к увеличению, не требуя, чтобы это увеличение было представлено линейной зависимостью. Если при увеличении одной переменной другая уменьшается , коэффициенты ранговой корреляции будут отрицательными. Эти коэффициенты ранговой корреляции принято рассматривать как альтернативу коэффициенту Пирсона, используемую либо для уменьшения объема вычислений, либо для того, чтобы сделать коэффициент менее чувствительным к ненормальности в распределениях. Однако у этой точки зрения мало математической основы, поскольку коэффициенты ранговой корреляции измеряют другой тип отношений, чем коэффициент корреляции момента произведения Пирсона , и их лучше всего рассматривать как меры другого типа связи, а не как альтернативную меру генеральной совокупности. коэффициент корреляции. ^{[7] [8]}

Чтобы проиллюстрировать природу ранговой корреляции и ее отличие от линейной корреляции, рассмотрим следующие четыре пары чисел : ${\displaystyle (x,y)}$

(0, 1), (10, 100), (101, 500), (102, 2000).

По мере перехода от каждой пары к следующей увеличивается, как и . Эта связь идеальна в том смысле, что увеличение всегда сопровождается увеличением . Это означает, что у нас идеальная ранговая корреляция, и коэффициенты корреляции Спирмена и Кендалла равны 1, тогда как в этом примере коэффициент корреляции момента произведения Пирсона равен 0,7544, что указывает на то, что точки далеки от прямой линии. Точно так же, если всегда уменьшается при увеличении , коэффициенты ранговой корреляции будут равны -1, в то время как коэффициент корреляции момента произведения Пирсона может быть близок или не близок к -1, в зависимости от того, насколько близко точки расположены к прямой линии. Хотя в крайних случаях идеальной ранговой корреляции оба коэффициента равны (оба +1 или оба -1), обычно это не так, и поэтому значения двух коэффициентов не могут значимо сравниваться. ^[7] Например, для трех пар (1, 1) (2, 3) (3, 2) коэффициент Спирмена равен 1/2, а коэффициент Кендалла равен 1/3. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle x}$

Другие меры зависимости между случайными величинами

Информации, которую дает коэффициент корреляции, недостаточно для определения структуры зависимости между случайными величинами. ^[9] Коэффициент корреляции полностью определяет структуру зависимости только в очень частных случаях, например, когда распределение представляет собой многомерное нормальное распределение . (См. диаграмму выше.) В случае эллиптических распределений оно характеризует (гипер-)эллипсы равной плотности; однако оно не полностью характеризует структуру зависимости (например, степени свободы многомерного t-распределения определяют уровень хвостовой зависимости).

Дистанционная корреляция ^{[10] [11]} была введена для устранения недостатка корреляции Пирсона, заключающегося в том, что она может быть равна нулю для зависимых случайных величин; корреляция с нулевым расстоянием подразумевает независимость.

Коэффициент рандомизированной зависимости ^[12] представляет собой эффективную в вычислительном отношении меру зависимости между многомерными случайными величинами, основанную на связке . RDC инвариантен по отношению к нелинейному масштабированию случайных величин, способен обнаруживать широкий спектр шаблонов функциональных ассоциаций и принимает нулевое значение при независимости.

Для двух двоичных переменных отношение шансов измеряет их зависимость и принимает неотрицательные числа в диапазоне, возможно, бесконечность: . Связанные статистические данные, такие как Y Юла и Q Юла, нормализуют это до диапазона, подобного корреляции . Отношение шансов обобщается логистической моделью для моделирования случаев, когда зависимые переменные дискретны и может существовать одна или несколько независимых переменных. ${\displaystyle [0,+\infty ]}$ ${\displaystyle [-1,1]}$

Коэффициент корреляции , взаимная информация на основе энтропии , полная корреляция , двойная полная корреляция и полихорическая корреляция также способны обнаруживать более общие зависимости, как и рассмотрение связки между ними, в то время как коэффициент детерминации обобщает коэффициент корреляции до множественной регрессии. .

Чувствительность к распределению данных

Степень зависимости между переменными X и Y не зависит от масштаба, в котором выражены переменные. То есть, если мы анализируем взаимосвязь между X и Y , на большинство показателей корреляции не влияет преобразование X в a + bX и Y в c + dY , где a , b , c и d — константы ( b и d являются положительными ). Это справедливо как для некоторых корреляционных статистических данных , так и для их популяционных аналогов. Некоторые статистические данные корреляции, такие как коэффициент ранговой корреляции, также инвариантны к монотонным преобразованиям маргинальных распределений X и/или Y .

Коэффициенты корреляции Пирсона / Спирмена между X и Y показаны, когда диапазоны двух переменных неограничены, а также когда диапазон X ограничен интервалом (0,1).

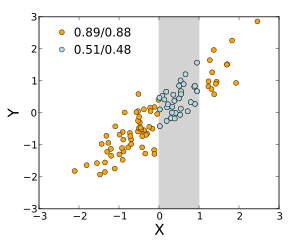
Большинство показателей корреляции чувствительны к способу выборки X и Y. Зависимости имеют тенденцию быть более сильными, если рассматривать их в более широком диапазоне значений. Таким образом, если мы рассмотрим коэффициент корреляции между ростом отцов и их сыновей для всех взрослых мужчин и сравним его с тем же коэффициентом корреляции, рассчитанным при выборе отцов ростом от 165 до 170 см, корреляция будет равна в последнем случае слабее. Было разработано несколько методов, пытающихся исправить ограничение диапазона одной или обеих переменных, и они обычно используются в метаанализе; наиболее распространенными являются уравнения Торндайка для случая II и случая III. ^[13]

Различные используемые меры корреляции могут быть неопределенными для некоторых совместных распределений X и Y. Например, коэффициент корреляции Пирсона определяется в терминах моментов и, следовательно, будет неопределенным, если моменты не определены. Всегда определяются меры зависимости, основанные на квантилях . Статистика на основе выборки, предназначенная для оценки показателей зависимости населения, может иметь или не иметь желаемые статистические свойства, такие как несмещенность или асимптотическая согласованность , в зависимости от пространственной структуры совокупности, из которой были отобраны данные.

Чувствительность к распределению данных может быть использована с выгодой. Например, масштабированная корреляция предназначена для использования чувствительности к диапазону для выявления корреляций между быстрыми компонентами временного ряда. ^[14] Путем контролируемого сокращения диапазона значений корреляции в долгосрочном масштабе отфильтровываются и выявляются только корреляции в коротких временных масштабах.

Матрицы корреляции

Корреляционная матрица случайных величин – это матрица , запись которой равна ${\displaystyle n}$ ${\displaystyle X_{1},\ldots ,X_{n}}$ ${\displaystyle n\times n}$ ${\displaystyle C}$ ${\displaystyle (i,j)}$

${\displaystyle c_{ij}:=\operatorname {corr} (X_{i},X_{j})={\frac {\operatorname {cov} (X_{i},X_{j})}{\sigma _{X_{i}}\sigma _{X_{j}}}},\quad {\text{if}}\ \sigma _{X_{i}}\sigma _{X_{j}}>0.}$

Таким образом, все диагональные элементы тождественно едины . Если используемыми мерами корреляции являются коэффициенты момента произведения, матрица корреляции такая же, как ковариационная матрица стандартизированных случайных величин для . Это относится как к матрице корреляций генеральной совокупности (в этом случае — стандартное отклонение генеральной совокупности), так и к матрице корреляций выборки (в этом случае обозначает стандартное отклонение выборки). Следовательно, каждая из них обязательно является положительно-полуопределенной матрицей . Более того, корреляционная матрица является строго положительно определенной, если ни одна переменная не может иметь все свои значения, точно сгенерированные как линейная функция значений других. ${\displaystyle X_{i}/\sigma (X_{i})}$ ${\displaystyle i=1,\dots ,n}$ ${\displaystyle \sigma }$ ${\displaystyle \sigma }$

Матрица корреляции симметрична, поскольку корреляция между и такая же, как корреляция между и . ${\displaystyle X_{i}}$ ${\displaystyle X_{j}}$ ${\displaystyle X_{j}}$ ${\displaystyle X_{i}}$

Корреляционная матрица появляется, например, в одной формуле для коэффициента множественной детерминации , меры согласия в множественной регрессии .

В статистическом моделировании корреляционные матрицы, представляющие отношения между переменными, подразделяются на различные корреляционные структуры, которые различаются такими факторами, как количество параметров, необходимых для их оценки. Например, в сменной корреляционной матрице все пары переменных моделируются как имеющие одинаковую корреляцию, поэтому все недиагональные элементы матрицы равны друг другу. С другой стороны, авторегрессионная матрица часто используется, когда переменные представляют временной ряд, поскольку корреляции, вероятно, будут выше, когда измерения ближе по времени. Другие примеры включают независимый, неструктурированный, M-зависимый и Теплиц .

При исследовательском анализе данных иконография корреляций состоит в замене корреляционной матрицы диаграммой, где «замечательные» корреляции представлены сплошной линией (положительная корреляция) или пунктирной линией (отрицательная корреляция).

Ближайшая действительная корреляционная матрица

В некоторых приложениях (например, при построении моделей данных только на основе частично наблюдаемых данных) требуется найти «ближайшую» корреляционную матрицу к «приблизительной» корреляционной матрице (например, матрице, которой обычно не хватает полуопределенной положительности из-за того, как она имеет было вычислено).

В 2002 году Хайэм ^[15] формализовал понятие близости, используя норму Фробениуса , и предоставил метод вычисления ближайшей корреляционной матрицы с использованием алгоритма проекции Дикстры , реализация которого доступна в виде онлайн-веб-API. ^[16]

Это вызвало интерес к предмету, поскольку в последующие годы были получены новые теоретические (например, вычисление ближайшей корреляционной матрицы с факторной структурой ^[17] ) и численные (например, использование метода Ньютона для вычисления ближайшей корреляционной матрицы ^{[18] ).}

Некоррелированность и независимость случайных процессов

Аналогично для двух случайных процессов и : если они независимы, то они некоррелированы. ^{[19] : с. 151} Противоположное этому утверждению может быть неверным. Даже если две переменные некоррелированы, они могут не быть независимыми друг от друга. ${\displaystyle \left\{X_{t}\right\}_{t\in {\mathcal {T}}}}$ ${\displaystyle \left\{Y_{t}\right\}_{t\in {\mathcal {T}}}}$

Распространенные заблуждения

Корреляция и причинность

Традиционное утверждение о том, что « корреляция не подразумевает причинно-следственную связь », означает, что корреляция сама по себе не может использоваться для вывода о причинно-следственной связи между переменными. ^[20] Это изречение не следует понимать в том смысле, что корреляции не могут указывать на потенциальное существование причинно-следственных связей. Однако причины, лежащие в основе корреляции, если таковые имеются, могут быть косвенными и неизвестными, а высокие корреляции также перекрываются тождественными отношениями ( тавтологиями ), где причинного процесса не существует. Следовательно, корреляция между двумя переменными не является достаточным условием для установления причинно-следственной связи (в любом направлении).

Причинно-следственная связь между возрастом и ростом у детей довольно прозрачна, а вот корреляция между настроением и здоровьем у людей менее очевидна. Приводит ли улучшение настроения к улучшению здоровья, или хорошее здоровье приводит к хорошему настроению, или и то, и другое? Или в основе обоих лежит какой-то другой фактор? Другими словами, корреляция может рассматриваться как свидетельство возможной причинной связи, но не может указывать на то, какой может быть причинная связь, если таковая имеется.

Простые линейные корреляции

Квартет Анскомба : четыре набора данных с одинаковой корреляцией 0,816.

Коэффициент корреляции Пирсона указывает на силу линейной связи между двумя переменными, но его значение, как правило, не полностью характеризует их взаимосвязь. ^[21] В частности, если условное среднее заданного , обозначенное , не является линейным по , коэффициент корреляции не будет полностью определять форму . ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle \operatorname {E} (Y\mid X)}$ ${\displaystyle X}$ ${\displaystyle \operatorname {E} (Y\mid X)}$

На соседнем изображении показаны диаграммы рассеяния квартета Анскомба — набора из четырех различных пар переменных, созданных Фрэнсисом Анскомбом . ^[22] Четыре переменные имеют одинаковое среднее значение (7,5), дисперсию (4,12), корреляцию (0,816) и линию регрессии ( ). Однако, как видно на графиках, распределение переменных сильно различается. Первый из них (вверху слева), по-видимому, распределяется нормально и соответствует тому, что можно было бы ожидать, рассматривая две коррелированные переменные и следуя предположению о нормальности. Второй (справа вверху) не распространяется нормально; хотя можно наблюдать очевидную связь между двумя переменными, она не является линейной. В этом случае коэффициент корреляции Пирсона не указывает на наличие точной функциональной зависимости: только степень, в которой эта связь может быть аппроксимирована линейной зависимостью. В третьем случае (внизу слева) линейная зависимость идеальна, за исключением одного выброса , который оказывает достаточное влияние, чтобы снизить коэффициент корреляции с 1 до 0,816. Наконец, четвертый пример (внизу справа) показывает еще один пример, когда одного выброса достаточно для получения высокого коэффициента корреляции, даже несмотря на то, что связь между двумя переменными не является линейной. ${\displaystyle y}$ ${\textstyle y=3+0.5x}$

Эти примеры показывают, что коэффициент корреляции как сводная статистика не может заменить визуальный анализ данных. Иногда говорят, что эти примеры демонстрируют, что корреляция Пирсона предполагает, что данные подчиняются нормальному распределению , но это верно лишь частично. ^[4] Корреляцию Пирсона можно точно рассчитать для любого распределения, имеющего конечную ковариационную матрицу , которая включает большинство распределений, встречающихся на практике. Однако коэффициент корреляции Пирсона (вместе с выборочным средним и дисперсией) является достаточной статистикой только в том случае, если данные получены из многомерного нормального распределения . В результате коэффициент корреляции Пирсона полностью характеризует связь между переменными тогда и только тогда, когда данные взяты из многомерного нормального распределения.

Двумерное нормальное распределение

Если пара случайных величин следует двумерному нормальному распределению , условное среднее является линейной функцией от , а условное среднее является линейной функцией от Коэффициент корреляции между и и маргинальными средними и дисперсиями и определяет эту линейную зависимость: ${\displaystyle \ (X,Y)\ }$ ${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (X\mid Y)}$ ${\displaystyle Y}$ ${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (Y\mid X)}$ ${\displaystyle \ X~.}$ ${\displaystyle \ \rho _{X,Y}\ }$ ${\displaystyle \ X\ }$ ${\displaystyle \ Y\ ,}$ ${\displaystyle \ X\ }$ ${\displaystyle \ Y\ }$

${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (Y\mid X)=\operatorname {\boldsymbol {\mathcal {E}}} (Y)+\rho _{X,Y}\cdot \sigma _{Y}\cdot {\frac {\ X-\operatorname {\boldsymbol {\mathcal {E}}} (X)\ }{\sigma _{X}}}\ ,}$

где и — ожидаемые значения и соответственно, и — стандартные отклонения и соответственно. ${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (X)}$ ${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (Y)}$ ${\displaystyle \ X\ }$ ${\displaystyle \ Y\ ,}$ ${\displaystyle \ \sigma _{X}\ }$ ${\displaystyle \ \sigma _{Y}\ }$ ${\displaystyle \ X\ }$ ${\displaystyle \ Y\ ,}$

Эмпирическая корреляция представляет собой оценку коэффициента корреляции. Оценка распределения определяется выражением ${\displaystyle r}$ ${\displaystyle \ \rho ~.}$ ${\displaystyle \ \rho \ }$

$${\displaystyle \pi (\rho \mid r)={\frac {\ \Gamma (N)\ }{\ {\sqrt {2\pi \ }}\cdot \Gamma (N-{\tfrac {\ 1\ }{2}})\ }}\cdot {\bigl (}1-r^{2}{\bigr )}^{\frac {\ N\ -2\ }{2}}\cdot {\bigl (}1-\rho ^{2}{\bigr )}^{\frac {\ N-3\ }{2}}\cdot {\bigl (}1-r\rho {\bigr )}^{-N+{\frac {\ 3\ }{2}}}\cdot F_{\mathsf {Hyp}}\left(\ {\tfrac {\ 3\ }{2}},-{\tfrac {\ 1\ }{2}};N-{\tfrac {\ 1\ }{2}};{\frac {\ 1+r\rho \ }{2}}\ \right)\ }$$

где – гипергеометрическая функция Гаусса . ${\displaystyle \ F_{\mathsf {Hyp}}\ }$

Эта плотность является одновременно байесовской апостериорной плотностью и точной оптимальной плотностью доверительного распределения . ^{[23] [24]}

Смотрите также

• Математический портал

• Автокорреляция
• Каноническая корреляция
• Коэффициент детерминации
• Коинтеграция
• Коэффициент согласованности корреляции
• Кофенетическая корреляция
• Ослабление корреляции
• Корреляционная функция
• Корреляционный разрыв
• Ковариация
• Ковариация и корреляция
• Взаимная корреляция
• Экологическая корреляция
• Доля дисперсии необъяснима
• Генетическая корреляция
• Лямбда Гудмана и Краскала
• Иконография корреляций
• Иллюзорная корреляция
• Межклассовая корреляция
• Внутриклассовая корреляция
• Лифт (интеллектуальный анализ данных)
• Средняя зависимость
• Проблема с изменяемой единицей площади
• Множественная корреляция
• Коэффициент точечно-бисерийной корреляции
• Соотношение количества квадрантов
• Ложная корреляция
• Статистическое корреляционное соотношение
• Субнезависимость

Рекомендации

1. Крокстон, Фредерик Эмори; Кауден, Дадли Джонстон; Кляйн, Сидней (1968) Общая прикладная статистика , Питман. ISBN  9780273403159 (стр. 625)
2. Дитрих, Корнелиус Франк (1991) Неопределенность, калибровка и вероятность: статистика научных и промышленных измерений, 2-е издание, А. Хиглер. ISBN 9780750300605 (стр. 331) 
3. Эйткен, Александр Крейг (1957) Статистическая математика, 8-е издание. Оливер и Бойд. ISBN 9780050013007 (стр. 95) 
4. Роджерс, JL; Найсвандер, Вашингтон (1988). «Тринадцать способов взглянуть на коэффициент корреляции». Американский статистик . 42 (1): 59–66. дои : 10.1080/00031305.1988.10475524. JSTOR  2685263.
5. Дауди, С. и Уирден, С. (1983). «Статистика для исследований», Уайли. ISBN 0-471-08602-9, стр. 230. 
6. Фрэнсис, ДП; Пальто AJ; Гибсон Д. (1999). «Насколько высоким может быть коэффициент корреляции?». Инт Джей Кардиол . 69 (2): 185–199. дои : 10.1016/S0167-5273(99)00028-5. ПМИД  10549842.
7. Юл, Г.Ю. и Кендалл, М.Г. (1950), «Введение в теорию статистики», 14-е издание (5-е впечатление, 1968 г.). Чарльз Гриффин и компания, стр. 258–270.
8. Кендалл, М.Г. (1955) «Методы ранговой корреляции», Charles Griffin & Co.
9. Махдави Дамгани Б. (2013). «Не вводящая в заблуждение ценность предполагаемой корреляции: введение в модель коинтеляции». Журнал Уилмотт . 2013 (67): 50–61. дои : 10.1002/wilm.10252.
10. Секели, Г. Дж. Риццо; Бакиров, НК (2007). «Измерение и проверка независимости путем корреляции расстояний». Анналы статистики . 35 (6): 2769–2794. arXiv : 0803.4101 . дои : 10.1214/009053607000000505. S2CID  5661488.
11. Секели, Г.Дж.; Риццо, МЛ (2009). «Ковариация броуновского расстояния». Анналы прикладной статистики . 3 (4): 1233–1303. arXiv : 1010.0297 . дои : 10.1214/09-AOAS312. ПМЦ 2889501 . ПМИД  20574547. 
12. Лопес-Пас Д., Хенниг П. и Шёлкопф Б. (2013). «Коэффициент рандомизированной зависимости», « Конференция по нейронным системам обработки информации », перепечатка
13. Торндайк, Роберт Лэдд (1947). Проблемы и методы исследования (Отчет №3) . Вашингтон, округ Колумбия: Правительство США. Распечатать. выключенный.
14. Николич, Д; Муресан, РЦ; Фэн, В; Сингер, Вт (2012). «Масштабный корреляционный анализ: лучший способ вычисления кросс-коррелограммы». Европейский журнал неврологии . 35 (5): 1–21. дои : 10.1111/j.1460-9568.2011.07987.x. PMID  22324876. S2CID  4694570.
15. Хайэм, Николас Дж. (2002). «Вычисление ближайшей корреляционной матрицы — задача из финансов». Журнал IMA численного анализа . 22 (3): 329–343. CiteSeerX 10.1.1.661.2180 . дои : 10.1093/иманум/22.3.329. 
16. «Оптимизатор портфеля». портфолиооптимизатор.io . Проверено 30 января 2021 г.
17. Борсдорф, Рюдигер; Хайэм, Николас Дж.; Райдан, Маркос (2010). «Вычисление матрицы ближайшей корреляции с факторной структурой» (PDF) . СИАМ Дж. Матричный анал. Приложение . 31 (5): 2603–2622. дои : 10.1137/090776718.
18. Ци, ХОУДУО; Сунь, ДЭФЭН (2006). «Квадратично сходящийся метод Ньютона для вычисления ближайшей корреляционной матрицы». СИАМ Дж. Матричный анал. Приложение . 28 (2): 360–385. дои : 10.1137/050624509.
19. Пак, Кун Иль (2018). Основы теории вероятности и случайных процессов с приложениями к средствам связи . Спрингер. ISBN 978-3-319-68074-3.
20. Олдрич, Джон (1995). «Подлинные и ложные корреляции у Пирсона и Юла». Статистическая наука . 10 (4): 364–376. дои : 10.1214/ss/1177009870 . JSTOR  2246135.
21. Махдави Дамгани, Бабак (2012). «Вводящая в заблуждение ценность измеренной корреляции». Журнал Уилмотт . 2012 (1): 64–73. дои : 10.1002/wilm.10167. S2CID  154550363.
22. Анскомб, Фрэнсис Дж. (1973). «Графики в статистическом анализе». Американский статистик . 27 (1): 17–21. дои : 10.2307/2682899. JSTOR  2682899.
23. Таральдсен, Гуннар (2021). «Доверительная плотность корреляции». Санкхья А. 85 : 600–616. дои : 10.1007/s13171-021-00267-y . ISSN  0976-8378. S2CID  244594067.
24. Таральдсен, Гуннар (2020). Уверенность в корреляции. Researchgate.net (препринт). дои : 10.13140/RG.2.2.23673.49769.

дальнейшее чтение

• Коэн, Дж.; Коэн П.; Уэст, С.Г. и Эйкен, Л.С. (2002). Прикладной множественный регрессионно-корреляционный анализ для поведенческих наук (3-е изд.). Психология Пресс. ISBN 978-0-8058-2223-6.
• «Корреляция (в статистике)», Математическая энциклопедия , EMS Press , 2001 [1994]
• Острайхер, Дж. и Д.Р. (26 февраля 2015 г.). «Чума равных»: научный триллер о международных заболеваниях, политике и открытии лекарств . Калифорния: Omega Cat Press. п. 408. ИСБН 978-0963175540.

Внешние ссылки

• Страница MathWorld, посвященная коэффициентам (взаимной) корреляции выборки
• Вычислите значимость между двумя корреляциями для сравнения двух значений корреляции.
• "A MATLAB Toolbox for computing Weighted Correlation Coefficients". Archived from the original on 24 April 2021.
• Proof that the Sample Bivariate Correlation has limits plus or minus 1
• Interactive Flash simulation on the correlation of two normally distributed variables by Juha Puranen.
• Correlation analysis. Biomedical Statistics
• R-Psychologist Correlation visualization of correlation between two numeric variables