Пустой набор

Математический набор, не содержащий элементов

Пустое множество — это множество, не содержащее элементов.

В математике пустое множество — это уникальное множество , не содержащее элементов ; его размер или мощность (количество элементов в наборе) равны нулю . ^[1] Некоторые аксиоматические теории множеств гарантируют, что пустое множество существует, включая аксиому пустого множества , в то время как в других теориях его существование может быть выведено. Многие возможные свойства множеств бессмысленно верны для пустого множества.

Любое множество, кроме пустого, называется непустым.

В некоторых учебниках и популяризациях пустой набор называется «нулевым набором». ^[1] Однако нулевое множество — это отдельное понятие в контексте теории меры , в которой оно описывает множество нулевой меры (которое не обязательно пусто).

Обозначения

Символ пустого множества

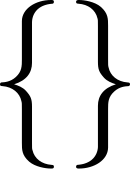
Общие обозначения пустого набора включают «{ }», « » и «∅». Последние два символа были введены группой Бурбаки (в частности, Андре Вейлем ) в 1939 году по мотивам буквы Ø в датском и норвежском алфавитах. ^[2] В прошлом «0» (цифра ноль ) иногда использовалась как символ пустого множества, но теперь это считается неправильным использованием обозначения. ^[3] ${\displaystyle \emptyset }$

Символ ∅ доступен в точке Юникода U+2205. ^[4] Его можно закодировать в HTML как ∅и как ∅. Его можно закодировать в LaTeX как \varnothing. Символ кодируется в LaTeX как . ${\displaystyle \emptyset }$\emptyset

При написании на таких языках, как датский и норвежский, где символ пустого набора можно спутать с буквой Ø (как при использовании этого символа в лингвистике), вместо него можно использовать символ Юникода U+29B0 REVERSED EMPTY SET ⦰. ^[5]

Характеристики

В стандартной аксиоматической теории множеств по принципу экстенсиональности два множества равны, если они имеют одинаковые элементы (то есть ни в одном из них нет элемента, которого нет в другом). В результате может быть только один набор без элементов, поэтому используется термин «пустой набор», а не «пустой набор».

Единственное подмножество пустого множества — это само пустое множество; эквивалентно, набор мощности пустого набора - это набор, содержащий только пустой набор. Число элементов пустого множества (т. е. его мощность ) равно нулю. Пустой набор — единственный набор, обладающий любым из этих свойств.

Для любого набора А :

• Пустое множество является подмножеством A
• Объединение A с пустым множеством есть A
• Пересечение A с пустым множеством является пустым множеством .
• Декартово произведение A и пустого множества — это пустое множество .

Для любого свойства P :

• Для каждого элемента свойство P выполняется ( пустая истина ). ${\displaystyle \varnothing }$
• Не существует элемента, для которого выполнялось бы свойство P. ${\displaystyle \varnothing }$

И наоборот, если для некоторого свойства P и некоторого множества V справедливы следующие два утверждения:

• Для каждого элемента V имеет место свойство P.
• Не существует элемента V , для которого выполнено свойство P.

затем ${\displaystyle V=\varnothing .}$

По определению подмножества пустое множество является подмножеством любого множества A. То есть каждый элемент x принадлежит A . Действительно, если бы не было верно, что каждый элемент находится в A , то существовал бы хотя бы один элемент, которого нет в A. Поскольку элементов a вообще нет , нет элемента a, которого не было бы в A. Любое утверждение, начинающееся со слов «для каждого элемента », не является каким-либо существенным утверждением; это пустая истина . Это часто перефразируют как «все верно для элементов пустого множества». ${\displaystyle \varnothing }$ ${\displaystyle \varnothing }$ ${\displaystyle \varnothing }$ ${\displaystyle \varnothing }$ ${\displaystyle \varnothing }$ ${\displaystyle \varnothing }$

В обычном теоретико-множественном определении натуральных чисел ноль моделируется пустым множеством.

Операции над пустым множеством

Говоря о сумме элементов конечного множества, неизбежно приходим к соглашению, что сумма элементов пустого множества равна нулю. Причина этого в том, что нуль является единичным элементом сложения. Аналогично, произведение элементов пустого множества следует считать равным единице (см. пустое произведение ), поскольку единица является единичным элементом для умножения. ^{[ нужна цитата ]}

Расстройство — это перестановка множества без неподвижных точек . Пустое множество можно рассматривать как нарушение само по себе, потому что оно имеет только одну перестановку ( ), и совершенно верно, что не может быть найден ни один элемент (пустого набора), который сохранял бы свое исходное положение. ${\displaystyle 0!=1}$

В других областях математики

Расширенные действительные числа

Поскольку пустое множество не имеет члена, когда оно рассматривается как подмножество любого упорядоченного набора , каждый член этого набора будет верхней и нижней границей пустого набора. Например, если рассматривать его как подмножество действительных чисел с его обычным порядком, представленным линией действительных чисел , каждое действительное число является одновременно верхней и нижней границей пустого набора. ^[6] Если рассматривать его как подмножество расширенных действительных чисел , образованное добавлением двух «числ» или «точек» к действительным числам (а именно, отрицательной бесконечности , определяемой как меньше любого другого расширенного действительного числа, и положительной бесконечности , (обозначается как большее, чем любое другое расширенное действительное число), мы имеем следующее: ${\displaystyle -\infty \!\,,}$ ${\displaystyle +\infty \!\,,}$

$${\displaystyle \sup \varnothing =\min(\{-\infty ,+\infty \}\cup \mathbb {R} )=-\infty ,}$$

$${\displaystyle \inf \varnothing =\max(\{-\infty ,+\infty \}\cup \mathbb {R} )=+\infty .}$$

То есть наименьшая верхняя граница (sup или supremum ) пустого набора — это отрицательная бесконечность, а наибольшая нижняя граница (inf или infimum ) — положительная бесконечность. По аналогии с вышеизложенным, в области расширенных действительных чисел отрицательная бесконечность является единицей для операторов максимума и верхней границы, а положительная бесконечность является единицей для операторов минимума и нижней границы.

Топология

В любом топологическом пространстве X пустое множество открыто по определению, как и X . Поскольку дополнение открытого множества закрыто , а пустое множество и X являются дополнениями друг друга, пустое множество также закрыто, что делает его открыто-закрытым множеством . Более того, пустое множество компактно в силу того, что каждое конечное множество компактно.

Замыкание пустого множества пусто . Это известно как «сохранение нулевых союзов ».

Теория категорий

Если множество, то существует ровно одна функция от до пустой функции . В результате пустое множество является единственным исходным объектом категории множеств и функций . ${\displaystyle A}$ ${\displaystyle f}$ ${\displaystyle \varnothing }$ ${\displaystyle A,}$

Пустое множество можно превратить в топологическое пространство , называемое пустым пространством, только одним способом: определив пустое множество как открытое . Это пустое топологическое пространство является единственным исходным объектом в категории топологических пространств с непрерывными отображениями . Фактически, это строгий исходный объект : только пустое множество имеет функцию для пустого множества.

Теория множеств

В конструкции фон Неймана ординалов 0 определяется как пустое множество, а последующий ординал определяется как . Таким образом, мы имеем , , , и так далее. Конструкция фон Неймана вместе с аксиомой бесконечности , которая гарантирует существование хотя бы одного бесконечного множества, может использоваться для построения набора натуральных чисел , такого, что аксиомы арифметики Пеано удовлетворяются. ${\displaystyle S(\alpha )=\alpha \cup \{\alpha \}}$ ${\displaystyle 0=\varnothing }$ ${\displaystyle 1=0\cup \{0\}=\{\varnothing \}}$ ${\displaystyle 2=1\cup \{1\}=\{\varnothing ,\{\varnothing \}\}}$ ${\displaystyle \mathbb {N} _{0}}$

Под вопросом существование

Исторические проблемы

В контексте наборов действительных чисел Кантор имел обыкновение обозначать « не содержит ни одной точки». Это обозначение использовалось в определениях, например, Кантор определил два множества как непересекающиеся, если в их пересечении нет точек, однако остается спорным, рассматривал ли Кантор как существующее множество само по себе или Кантор просто использовал его как предикат пустоты. Цермело воспринимал себя как набор, но считал его «неподходящим набором». ^[7] ${\displaystyle P\equiv O}$ ${\displaystyle P}$ ${\displaystyle \equiv O}$ ${\displaystyle O}$ ${\displaystyle \equiv O}$ ${\displaystyle O}$

Аксиоматическая теория множеств

В теории множеств Цермело существование пустого множества обеспечивается аксиомой пустого множества , а его единственность следует из аксиомы экстенсиональности . Однако аксиому пустого множества можно показать избыточной как минимум двумя способами:

• Стандартная логика первого порядка подразумевает, просто исходя из логических аксиом , что что-то существует, и, говоря языком теории множеств, эта вещь должна быть множеством. Теперь существование пустого множества легко следует из аксиомы разделения .
• Даже используя свободную логику (которая логически не подразумевает, что что-то существует), уже существует аксиома, подразумевающая существование хотя бы одного множества, а именно аксиома бесконечности .

Философские вопросы

Хотя пустое множество является стандартной и широко распространенной математической концепцией, оно остается онтологической диковинкой, значение и полезность которой обсуждаются философами и логиками.

Пустое множество — это не то же самое, что ничто ; скорее, это набор, внутри которого нет ничего , а набор — это всегда что-то . Эту проблему можно решить, рассматривая набор как сумку — пустая сумка, несомненно, все еще существует. Дарлинг (2004) объясняет, что пустое множество — это не ничто, а скорее «набор всех треугольников с четырьмя сторонами, набор всех чисел, которые больше девяти, но меньше восьми, и набор всех дебютных ходов в шахматах , которые привлечь короля ». ^[8]

Популярный силлогизм

Нет ничего лучше, чем вечное счастье; бутерброд с ветчиной лучше, чем ничего; поэтому бутерброд с ветчиной лучше, чем вечное счастье

часто используется для демонстрации философской связи между концепцией ничего и пустым множеством. Дарлинг пишет, что контраст можно увидеть, переписав утверждения «Нет ничего лучше, чем вечное счастье» и «Сэндвич с ветчиной лучше, чем ничего» в математическом тоне. По словам Дарлинга, первое эквивалентно «Набору всех вещей, которые лучше, чем вечное счастье », а второе — «Набор {сэндвич с ветчиной} лучше, чем набор ». Первый сравнивает элементы множеств, а второй сравнивает сами множества. ^[8] ${\displaystyle \varnothing }$ ${\displaystyle \varnothing }$

Джонатан Лоу утверждает, что, хотя пустое множество

несомненно, была важной вехой в истории математики… мы не должны предполагать, что ее полезность в вычислениях зависит от того, действительно ли она обозначает какой-то объект.

также имеет место следующее:

«Все, что нам когда-либо сообщали о пустом множестве, это то, что оно (1) является множеством, (2) не имеет членов и (3) является уникальным среди множеств, поскольку не имеет членов. Однако есть очень много вещей, которые не имеют членов" в теоретико-множественном смысле, а именно, все не-множества. Совершенно ясно, почему эти вещи не имеют членов, поскольку они не являются множествами. Неясно, как может существовать единственное среди множеств множество , у которого нет членов. Мы не можем вызвать к существованию такую ​​сущность простым условием». ^[9]

Джордж Булос утверждал, что многое из того, что до сих пор было получено с помощью теории множеств, может быть так же легко получено путем количественной оценки множественного числа индивидов, без материализации множеств как единичных сущностей, имеющих другие сущности в качестве членов. ^[10]

Смотрите также

•  – ЧислоPages displaying short descriptions with no spaces
• Обитаемое множество  - свойство множеств, используемых в конструктивной математике.
• Ничего  – Полное отсутствие чего-либо; противоположность всему
• Набор мощности  - математический набор, содержащий все подмножества данного набора.

Рекомендации

1. Вайсштейн, Эрик В. «Пустой набор». mathworld.wolfram.com . Проверено 11 августа 2020 г.
2. «Самое раннее использование символов теории множеств и логики».
3. Рудин, Уолтер (1976). Принципы математического анализа (3-е изд.). МакГроу-Хилл. п. 300. ИСБН 007054235X.
4. «Стандарт Юникод 5.2» (PDF) .
5. например, Нина Грённум (2005, 2013) Фонетика и фонология: Almen og dansk. Академик Форлаг, Копенгаген.
6. Брукнер, А.Н., Брукнер, Дж.Б., и Томсон, Б.С. (2008). Элементарный реальный анализ , 2-е издание, с. 9.
7. А. Канамори, «Пустое множество, синглтон и упорядоченная пара», стр.275. Бюллетень символической логики, том. 9, нет. 3, (2003). По состоянию на 21 августа 2023 г.
8. DJ Darling (2004). Универсальная книга по математике . Джон Уайли и сыновья . п. 106. ИСБН 0-471-27047-4.
9. Э. Дж. Лоу (2005). Локк . Рутледж . п. 87.
10. Джордж Булос (1984), «Быть ​​— значит быть значением переменной», The Journal of Philosophy 91: 430–49. Переиздано в 1998 году, «Логика, логика и логика» ( Ричард Джеффри и Берджесс Дж., ред.) Harvard University Press , 54–72.

дальнейшее чтение

• Халмос, Пол , Наивная теория множеств . Принстон, Нью-Джерси: Компания Д. Ван Ностранда, 1960. Перепечатано Springer-Verlag, Нью-Йорк, 1974. ISBN 0-387-90092-6 (издание Springer-Verlag). Перепечатано Martino Fine Books, 2011. ISBN 978-1-61427-131-4 (издание в мягкой обложке).  
• Джех, Томас (2002), Теория множеств , Монографии Спрингера по математике (изд. 3-го тысячелетия), Springer, ISBN 3-540-44085-2
• Грэм, Малкольм (1975), Современная элементарная математика (2-е изд.), Харкорт Брейс Йованович , ISBN 0155610392

Внешние ссылки

• Вайсштейн, Эрик В. «Пустой набор». Математический мир .