Число Рейнольдса

Отношение инерционных и вязких сил, действующих на жидкость

Шлейф пламени этой свечи переходит от ламинарного к турбулентному.

Переход от ламинарного (слева) к турбулентному (справа) потоку воды из крана происходит по мере увеличения числа Рейнольдса.

Вихревая улица вокруг цилиндра. Это может произойти вокруг цилиндров и сфер для любой жидкости, размера цилиндра и скорости жидкости при условии, что число Рейнольдса находится между примерно 40 и 1000. ^[1]

Джордж Стоукс представил числа Рейнольдса.

Осборн Рейнольдс популяризировал эту концепцию.

В гидродинамике число Рейнольдса ( Re ) — это безразмерная величина , которая помогает прогнозировать характер течения жидкости в различных ситуациях путем измерения соотношения между инерционными и вязкими силами. При низких числах Рейнольдса в потоках преобладает ламинарный (листообразный) поток , тогда как при высоких числах Рейнольдса потоки имеют тенденцию быть турбулентными . Турбулентность возникает из-за различий в скорости и направлении жидкости, которые иногда могут пересекаться или даже двигаться против общего направления потока ( вихревые токи ). Эти вихревые токи начинают перемешивать поток, расходуя при этом энергию, что для жидкостей увеличивает вероятность кавитации .

Число Рейнольдса имеет широкое применение: от течения жидкости в трубе до прохождения воздуха над крылом самолета. Он используется для прогнозирования перехода от ламинарного потока к турбулентному и используется для масштабирования аналогичных ситуаций с потоком разного размера, например, между моделью самолета в аэродинамической трубе и полноразмерной версией. Прогнозы возникновения турбулентности и возможность расчета эффектов масштабирования могут быть использованы для прогнозирования поведения жидкости в более широком масштабе, например, при локальном или глобальном движении воздуха или воды, и, следовательно, связанных с этим метеорологических и климатологических эффектов.

Эта концепция была введена Джорджем Стоксом в 1851 году ^[2] , но число Рейнольдса было названо Арнольдом Зоммерфельдом в 1908 году ^[3] в честь Осборна Рейнольдса (1842–1912), который популяризировал его использование в 1883 году. ^{[4] [5]}

Определение

Число Рейнольдса — это отношение сил инерции к силам вязкости внутри жидкости, которая подвергается относительному внутреннему движению из-за разных скоростей жидкости. Область, в которой эти силы меняют поведение, известна как пограничный слой , например, ограничивающая поверхность внутри трубы. Аналогичный эффект создается при введении потока высокоскоростной жидкости в низкоскоростную, например горячих газов, выделяющихся из пламени в воздухе. Это относительное движение создает трение жидкости, которое является фактором развития турбулентного потока. Этому эффекту противодействует вязкость жидкости, которая имеет тенденцию подавлять турбулентность. Число Рейнольдса количественно определяет относительную важность этих двух типов сил для данных условий потока и является показателем того, когда турбулентный поток возникнет в конкретной ситуации. ^[6]

Эта способность прогнозировать начало турбулентного потока является важным инструментом проектирования такого оборудования, как системы трубопроводов или крылья самолета, но число Рейнольдса также используется при масштабировании задач гидродинамики и используется для определения динамического подобия между двумя различными случаями жидкости. поток, например, между моделью самолета и ее полноразмерной версией. Такое масштабирование не является линейным, и применение чисел Рейнольдса к обеим ситуациям позволяет разработать коэффициенты масштабирования.

По отношению к ламинарному и турбулентному режимам течения:

• ламинарный поток возникает при низких числах Рейнольдса, где преобладают силы вязкости, и характеризуется плавным, постоянным движением жидкости;
• турбулентный поток возникает при высоких числах Рейнольдса и в нем преобладают силы инерции, которые имеют тенденцию создавать хаотические водовороты , вихри и другие нестабильности потока. ^[7]

Число Рейнольдса определяется как ^[3]

${\displaystyle \mathrm {Re} ={\frac {uL}{\nu }}={\frac {\rho uL}{\mu }}}$

где:

• ρ — плотность жидкости ( единицы СИ : кг/м ³ ).
• u - скорость потока (м/с)
• L – характерная длина (м)
• μ — динамическая вязкость жидкости(Па·с или Н·с/м ² или кг/(м·с))
• ν – кинематическая вязкость жидкости (м ² /с).

Уравнение Брезины

Число Рейнольдса можно определить для нескольких различных ситуаций, когда жидкость движется относительно поверхности. ^{[n 1]} Эти определения обычно включают свойства жидкости, такие как плотность и вязкость, а также скорость и характерную длину или характерный размер (L в приведенном выше уравнении). Это измерение является предметом соглашения – например, радиус и диаметр одинаково подходят для описания сферы или круга, но один из них выбирается по соглашению. Для самолетов или кораблей можно использовать длину или ширину. Для течения в трубе или сферы, движущейся в жидкости, сегодня обычно используется внутренний диаметр. Другие формы, такие как прямоугольные трубы или несферические объекты, имеют определенный эквивалентный диаметр . Для жидкостей переменной плотности, таких как сжимаемые газы, или жидкостей переменной вязкости, таких как неньютоновские жидкости , применяются специальные правила. В некоторых обстоятельствах скорость также может быть условной, особенно в сосудах с перемешиванием.

На практике сопоставление числа Рейнольдса само по себе недостаточно для гарантии сходства. Поток жидкости обычно хаотичен, и очень небольшие изменения формы и шероховатости ограничивающих поверхностей могут привести к совершенно разным потокам. Тем не менее числа Рейнольдса являются очень важным ориентиром и широко используются.

Вывод

Если мы знаем, что соответствующими физическими величинами в физической системе являются только , то число Рейнольдса по существу фиксируется теоремой Букингема о π . ${\displaystyle \rho ,u,L,\mu }$

Подробно, поскольку величин 4 , но они имеют только 3 измерения (длина, время, масса), мы можем рассмотреть , где действительные числа. Установив три измерения равными нулю, мы получаем 3 независимых линейных ограничения, поэтому пространство решений имеет одно измерение и охватывается вектором . ${\displaystyle \rho ,u,L,\mu }$ ${\displaystyle \rho ^{x_{1}}u^{x_{2}}L^{x_{3}}\mu ^{x_{4}}}$ ${\displaystyle x_{1},...,x_{4}}$ ${\displaystyle \rho ^{x_{1}}u^{x_{2}}L^{x_{3}}\mu ^{x_{4}}}$ ${\displaystyle (1,1,1,-1)}$

Таким образом, любая безразмерная величина, построенная из, является функцией числа Рейнольдса. ${\displaystyle \rho ,u,L,\mu }$ ${\displaystyle \rho uL\mu ^{-1}}$

В качестве альтернативы мы можем взять уравнения Навье – Стокса для несжимаемой жидкости (конвективная форма) :

$${\displaystyle {\frac {\partial \mathbf {u} }{\partial t}}+(\mathbf {u} \cdot \nabla )\mathbf {u} -\nu \,\nabla ^{2}\mathbf {u} =-{\frac {1}{\rho }}\nabla p+\mathbf {g} }$$

теоремы Скаллопа ${\displaystyle {\mathbf {g}}}$ ${\displaystyle {\frac {\partial \mathbf {u} }{\partial t}}+(\mathbf {u} \cdot \nabla )\mathbf {u} }$ ${\displaystyle \nu \,\nabla ^{2}\mathbf {u} }$ ${\displaystyle {\frac {(\mathbf {u} \cdot \nabla )\mathbf {u} }{\nu \,\nabla ^{2}\mathbf {u} }}\sim {\frac {u^{2}/L}{\nu u/L^{2}}}={\frac {uL}{\nu }}}$

Альтернативный вывод

Число Рейнольдса можно получить, используя безразмерную форму уравнений Навье – Стокса несжимаемой жидкости для ньютоновской жидкости, выраженную через производную Лагранжа :

${\displaystyle \rho {\frac {D\mathbf {v} }{Dt}}=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {f} .}$

Каждый член в приведенном выше уравнении имеет единицы «массовой силы» (силы на единицу объема) с одинаковыми размерами плотности, умноженной на ускорение. Таким образом, каждый член зависит от точных измерений расхода. Если сделать уравнение безразмерным, то есть умножить его на коэффициент с обратными единицами основного уравнения, мы получим форму, не зависящую напрямую от физических размеров. Один из возможных способов получить безразмерное уравнение — умножить все уравнение на коэффициент

${\displaystyle {\frac {L}{\rho V^{2}}},}$

где

• V — средняя скорость v или v относительно жидкости (м/с),
• L – характерная длина (м),
• ρ – плотность жидкости (кг/м ³ ).

Если мы теперь установим

${\displaystyle {\begin{aligned}\mathbf {v} '&={\frac {\mathbf {v} }{V}},&p'&=p{\frac {1}{\rho V^{2}}},&\mathbf {f} '&=\mathbf {f} {\frac {L}{V^{2}}},&{\frac {\partial }{\partial t'}}&={\frac {L}{V}}{\frac {\partial }{\partial t}},&\nabla '&=L\nabla ,\end{aligned}}}$

мы можем переписать уравнение Навье – Стокса без размерностей:

${\displaystyle {\frac {D\mathbf {v} '}{Dt'}}=-\nabla 'p'+{\frac {\mu }{\rho LV}}\nabla '^{2}\mathbf {v} '+\mathbf {f} ',}$

где терминмкм/ρLV"="1/Ре.

Наконец, опустим простые числа для удобства чтения:

${\displaystyle {\frac {D\mathbf {v} }{Dt}}=-\nabla p+{\frac {1}{\mathrm {Re} }}\nabla ^{2}\mathbf {v} +\mathbf {f} .}$

Универсальное уравнение седиментации - коэффициент сопротивления, функция числа Рейнольдса и коэффициента формы, двумерная диаграмма.

Универсальное уравнение седиментации - коэффициент сопротивления, функция числа Рейнольдса и коэффициента формы, трехмерная диаграмма.

Вот почему математически все ньютоновские несжимаемые течения с одинаковым числом Рейнольдса сравнимы. Обратите также внимание, что в приведенном выше уравнении вязкие члены исчезают при Re → ∞ . Таким образом, потоки с высокими числами Рейнольдса в набегающем потоке примерно невязки.

История

Аппарат Осборна Рейнольдса 1883 года, демонстрирующий возникновение турбулентного потока. Аппарат все еще находится в Манчестерском университете.

Диаграмма из статьи Рейнольдса 1883 года, показывающая возникновение турбулентного потока.

Осборн Рейнольдс, как известно, изучал условия, при которых течение жидкости в трубах переходило от ламинарного течения к турбулентному . В своей статье 1883 года Рейнольдс описал переход от ламинарного потока к турбулентному в классическом эксперименте, в котором он исследовал поведение потока воды при различных скоростях потока, используя небольшой поток окрашенной воды, введенный в центр потока чистой воды в трубе большего размера.

Труба большего размера была стеклянной, поэтому можно было наблюдать за поведением слоя окрашенной струи. На конце этой трубы находился клапан регулирования потока, используемый для изменения скорости воды внутри трубы. При низкой скорости окрашенный слой оставался отчетливым по всей длине большой трубки. При увеличении скорости слой распадался в данной точке и диффундировал по всему поперечному сечению жидкости. Точка, в которой это произошло, была точкой перехода от ламинарного течения к турбулентному.

В результате этих экспериментов было получено безразмерное число Рейнольдса для динамического подобия — отношение сил инерции к силам вязкости . Рейнольдс также предложил то, что сейчас известно как усреднение Рейнольдса турбулентных потоков, где такие величины, как скорость, выражаются как сумма среднего и пульсирующего компонентов. Такое усреднение позволяет «объемное» описание турбулентного потока, например, с использованием усредненных по Рейнольдсу уравнений Навье – Стокса .

Поток в трубе

Для потока в трубе или трубке число Рейнольдса обычно определяется как ^[8]

${\displaystyle \mathrm {Re} ={\frac {uD_{\text{H}}}{\nu }}={\frac {\rho uD_{\text{H}}}{\mu }}={\frac {\rho QD_{\text{H}}}{\mu A}}={\frac {WD_{\text{H}}}{\mu A}},}$

где

• D _H — гидравлический диаметр трубы (внутренний диаметр, если труба имеет круглую форму) (м),
• Q – объемный расход (м ³ /с),
• A – площадь поперечного сечения трубы( A =πД ²/4) (м ² ),
• u — средняя скорость жидкости (м/с),
• μ (мю) — динамическая вязкость жидкости(Па·с = Н·с/м ² = кг/(м·с)),
• ν (nu) – кинематическая вязкость ( ν =мкм/ρ) (м ² /с),
• ρ (rho) – плотность жидкости (кг/м ³ ),
• W – массовый расход жидкости (кг/с).

Для таких форм, как квадратные, прямоугольные или кольцевые воздуховоды, высота и ширина которых сопоставимы, характерным размером для ситуаций с внутренним потоком считается гидравлический диаметр D _H , определяемый как

${\displaystyle D_{\text{H}}={\frac {4A}{P}},}$

где A — площадь поперечного сечения, а P — смоченный периметр . Смоченный периметр канала — это общий периметр всех стенок канала, соприкасающихся с потоком. ^[9] Это означает, что длина канала, контактирующего с воздухом, не включается в смоченный периметр.

Для круглой трубы гидравлический диаметр точно равен внутреннему диаметру трубы:

${\displaystyle D_{\text{H}}=D.}$

Для кольцевого канала, такого как внешний канал в теплообменнике «труба в трубе », гидравлический диаметр можно выразить алгебраически, чтобы уменьшить до

${\displaystyle D_{\text{H,annulus}}=D_{\text{o}}-D_{\text{i}},}$

где

• D _o — внутренний диаметр внешней трубы,
• D _i — внешний диаметр внутренней трубы.

Для расчета потока в некруглых воздуховодах гидравлический диаметр может быть заменен диаметром круглого воздуховода с достаточной точностью, если соотношение сторон AR поперечного сечения воздуховода остается в диапазоне1/4< АР < 4. ^[10]

Ламинарно-турбулентный переход

Эксперименты подтверждают, что при обтекании пограничного слоя плоской пластиной после определенной длины течения ламинарный пограничный слой становится неустойчивым и турбулентным. Эта нестабильность возникает в разных масштабах и с разными жидкостями, обычно когда Re _x ≈5 × 10 ⁵ , ^[11] где x — расстояние от передней кромки плоской пластины, а скорость потока — скорость набегающего потока жидкости вне пограничного слоя.

Для течения в трубе диаметром D экспериментальные наблюдения показывают, что для «полностью развитого» течения ^{[n 2]} ламинарное течение возникает, когда Re _D < 2300, и турбулентное течение возникает, когда Re D _> 2900. ^{[12] [13]} В нижнем конце этого диапазона образуется непрерывный турбулентный поток, но только на очень большом расстоянии от входа в трубу. Поток между ними начнет переходить от ламинарного к турбулентному, а затем обратно к ламинарному через нерегулярные промежутки времени, что называется прерывистым потоком. Это связано с различной скоростью и состоянием жидкости в разных областях поперечного сечения трубы, что зависит от других факторов, таких как шероховатость трубы и однородность потока. Ламинарный поток имеет тенденцию доминировать в быстро движущемся центре трубы, тогда как у стенки преобладает более медленно движущийся турбулентный поток. По мере увеличения числа Рейнольдса непрерывный турбулентный поток приближается к входному отверстию, и перемежаемость между ними увеличивается, пока поток не становится полностью турбулентным при Re _D > 2900. ^[12] Этот результат обобщается на некруглые каналы с использованием гидравлического уравнения . диаметр , позволяющий рассчитать переходное число Рейнольдса для других форм канала. ^[12]

Эти переходные числа Рейнольдса также называются критическими числами Рейнольдса и были изучены Осборном Рейнольдсом около 1895 года. ^[5] Критическое число Рейнольдса различно для каждой геометрии. ^[14]

Поток в широком воздуховоде

Для жидкости, движущейся между двумя плоскопараллельными поверхностями, ширина которых намного больше пространства между пластинами, характерный размер равен расстоянию между пластинами. ^[15] Это согласуется с приведенными выше случаями кольцевого воздуховода и прямоугольного воздуховода, взятыми с предельным соотношением сторон.

Течение в открытом канале

Для расчета течения жидкости со свободной поверхностью необходимо определить гидравлический радиус . Это площадь поперечного сечения канала, разделенная смоченным периметром. Для полукруглого канала он составляет четверть диаметра (в случае полной проходимости трубы). Для прямоугольного канала гидравлический радиус представляет собой площадь поперечного сечения, разделенную на смоченный периметр. В некоторых текстах затем используется характерный размер, в четыре раза превышающий гидравлический радиус, выбранный потому, что он дает то же значение Re для начала турбулентности, что и в трубопроводном потоке, ^[16], в то время как другие используют гидравлический радиус в качестве характерного масштаба длины с следовательно, разные значения Re для переходного и турбулентного течения.

Обтекание профилей

Числа Рейнольдса используются при проектировании профиля крыла , чтобы (среди прочего) управлять «эффектом масштаба» при вычислении/сравнении характеристик (крошечное крыло, масштабированное до огромных, будет работать по-другому). ^[17] Гидродинамики определяют хордовое число Рейнольдса R = Vc / ν , где V — скорость полета, c — длина хорды, а ν — кинематическая вязкость жидкости, в которой работает аэродинамический профиль, которая равна1,460 × 10 ⁻⁵  м ² /с для атмосферы на уровне моря . ^[18] В некоторых специальных исследованиях может использоваться другая характерная длина, кроме хорды; Редко встречается «число Рейнольдса размаха», которое не следует путать со станциями по размаху крыла, где до сих пор используется хорда. ^[19]

Объект в жидкости

Высокая вязкость меда приводит к идеально ламинарному потоку при выливании из ведра, а низкое поверхностное натяжение позволяет ему оставаться листообразным даже после достижения жидкости внизу. Аналогично турбулентности, когда поток встречает сопротивление, он замедляется и начинает колебаться взад и вперед, наслаиваясь на себя.

Число Рейнольдса для объекта, движущегося в жидкости, называемое числом Рейнольдса частицы и часто обозначаемое Re _p , характеризует характер окружающего потока и скорость его падения.

В вязких жидкостях

Ползучий поток мимо падающей сферы: линии тока , сила сопротивления F _d и сила тяжести F _g .

Там, где вязкость естественно высока, например, в растворах полимеров и расплавах полимеров, течение обычно ламинарное. Число Рейнольдса очень мало, и закон Стокса можно использовать для измерения вязкости жидкости. Сферам позволяют падать сквозь жидкость, и они быстро достигают конечной скорости , по которой можно определить вязкость.

Ламинарное течение растворов полимеров используется такими животными, как рыбы и дельфины, которые выделяют вязкие растворы из кожи, чтобы облегчить течение по телу во время плавания. Его использовали в гонках на яхтах владельцы, которые хотят получить преимущество в скорости, накачивая раствор полимера, такого как низкомолекулярный полиоксиэтилен в воде, по смачиваемой поверхности корпуса.

Однако это проблема при смешивании полимеров, поскольку для распределения мелкого наполнителя (например) по материалу необходима турбулентность. Такие изобретения, как «смеситель с перекачкой полости», были разработаны для создания нескольких складок в движущемся расплаве с целью повышения эффективности смешивания . Устройство можно установить на экструдеры для облегчения смешивания.

Сфера в жидкости

Коэффициент сопротивления C _d сферы как функция числа Рейнольдса Re , полученный в результате лабораторных экспериментов. Темная линия соответствует сфере с гладкой поверхностью, а более светлая линия соответствует случаю шероховатой поверхности (например, с небольшими ямочками). Существует диапазон скоростей жидкости, при котором мяч для гольфа с шероховатой поверхностью испытывает меньшее сопротивление, чем гладкий мяч. Цифры вдоль линии указывают на несколько режимов течения и связанные с ними изменения коэффициента сопротивления:

2. присоединенное течение ( поток Стокса ) и стационарное отрывное течение ,
3. отрывной нестационарный поток, имеющий ламинарный пограничный слой перед отрывом и образующий вихревую дорожку ,
4. отрывной нестационарный поток с ламинарным пограничным слоем на входной стороне, до отрыва потока, с хаотичным турбулентным следом за сферой ,
5. послекритическое отрывное течение с турбулентным пограничным слоем.

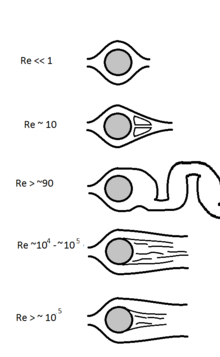
Для сферы в жидкости характерным масштабом длины является диаметр сферы, а характеристической скоростью является скорость сферы относительно жидкости на некотором расстоянии от сферы, так что движение сферы не нарушает эту точку отсчета. пакетик жидкости. Плотность и вязкость принадлежат жидкости. ^[20] Обратите внимание, что согласно этому определению чисто ламинарный поток существует только до Re = 10.

При условии малого Re связь между силой и скоростью движения определяется законом Стокса . ^[21]

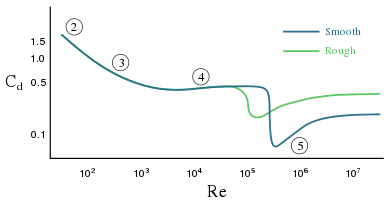
При более высоких числах Рейнольдса сопротивление сферы зависит от шероховатости поверхности. Так, например, добавление ямочек на поверхность мяча для гольфа приводит к тому, что пограничный слой на стороне перед мячом переходит из ламинарного в турбулентный. Турбулентный пограничный слой способен оставаться прикрепленным к поверхности шара гораздо дольше, чем ламинарная граница, и поэтому создает более узкий след низкого давления и, следовательно, меньшее сопротивление давлению. Уменьшение сопротивления давлению заставляет мяч двигаться дальше. ^[22]

Прямоугольный объект в жидкости

Уравнение прямоугольного объекта идентично уравнению сферы: объект аппроксимируется эллипсоидом, а ось длины выбирается в качестве характерного масштаба длины. Такие соображения важны, например, для природных водотоков, где мало зерен идеальной сферической формы. Для зерен, у которых измерение каждой оси нецелесообразно, вместо характерного масштаба длины частиц используются диаметры сит. Оба приближения изменяют значения критического числа Рейнольдса.

Скорость падения

Число Рейнольдса частицы важно для определения скорости падения частицы. Когда число Рейнольдса частицы указывает на ламинарный поток, закон Стокса можно использовать для расчета скорости ее падения или скорости осаждения. Когда число Рейнольдса частицы указывает на турбулентный поток, необходимо построить закон турбулентного сопротивления для моделирования соответствующей скорости осаждения.

Упакованная кровать

Для потока жидкости через слой контактирующих между собой примерно сферических частиц диаметром D , если объем пустот равен ε , а приведенная скорость равна v _s , число Рейнольдса можно определить как ^[23]

${\displaystyle \mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu }},}$

или

${\displaystyle \mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu \varepsilon }},}$

или

${\displaystyle \mathrm {Re} ={\frac {\rho v_{\text{s}}D}{\mu (1-\varepsilon )}}.}$

Выбор уравнения зависит от используемой системы: первое позволяет успешно коррелировать данные для различных типов насадочного и псевдоожиженного слоев , второе число Рейнольдса подходит для данных в жидкой фазе, а третье успешно коррелирует данные для псевдоожиженного слоя. данные, впервые представленные для системы с жидким псевдоожиженным слоем. ^[23]

Ламинарные условия применяются до Re = 10, полностью турбулентные — начиная с Re = 2000. ^[20]

Перемешиваемый сосуд

В цилиндрическом сосуде , перемешиваемом центральной вращающейся лопастью, турбиной или пропеллером, характерным размером является диаметр мешалки D. Скорость V равна ND , где N — скорость вращения в рад в секунду. Тогда число Рейнольдса равно:

${\displaystyle \mathrm {Re} ={\frac {\rho ND^{2}}{\mu }}={\frac {\rho VD}{\mu }}.}$

Система является полностью турбулентной при значениях Re выше10 000 . ^[24]

Трение трубы

Диаграмма Муди , которая описывает коэффициент трения Дарси-Вейсбаха f как функцию числа Рейнольдса и относительной шероховатости трубы.

Падение давления ^[25] , наблюдаемое при полностью развитом течении жидкости по трубам, можно спрогнозировать с помощью диаграммы Муди , которая отображает коэффициент трения Дарси-Вейсбаха f в зависимости от числа Рейнольдса Re и относительной шероховатости.ε/Д. На диаграмме четко показаны ламинарный, переходный и турбулентный режимы течения при увеличении числа Рейнольдса. Характер течения в трубе сильно зависит от того, является ли течение ламинарным или турбулентным.

Подобие потоков

Качественное поведение течения жидкости по цилиндру во многом зависит от числа Рейнольдса; подобные картины течения часто появляются, когда форма и число Рейнольдса совпадают, хотя другие параметры, такие как шероховатость поверхности, имеют большое влияние.

Чтобы два потока были похожими, они должны иметь одинаковую геометрию и равные числа Рейнольдса и Эйлера . При сравнении поведения жидкости в соответствующих точках модели и полномасштабного течения справедливо следующее:

${\displaystyle {\begin{aligned}\mathrm {Re} _{\text{m}}&=\mathrm {Re} ,\\\mathrm {Eu} _{\text{m}}&=\mathrm {Eu} ,\end{aligned}}}$

где – число Рейнольдса для модели, – полномасштабное число Рейнольдса, и аналогично для чисел Эйлера. ${\displaystyle \mathrm {Re} _{\text{m}}}$ ${\displaystyle \mathrm {Re} }$

Номера моделей и номера дизайна должны быть в одинаковой пропорции, следовательно,

${\displaystyle {\frac {p_{\text{m}}}{\rho _{\text{m}}v_{\text{m}}^{2}}}={\frac {p}{\rho v^{2}}}.}$

Это позволяет инженерам проводить эксперименты с моделями уменьшенного масштаба в водных каналах или аэродинамических трубах и сопоставлять данные с реальными потоками, экономя на затратах во время экспериментов и лабораторном времени. Обратите внимание, что истинное динамическое подобие может потребовать сопоставления и других безразмерных чисел , таких как число Маха, используемое в сжимаемых потоках , или число Фруда , которое управляет потоками в открытом канале. Некоторые потоки включают в себя больше безразмерных параметров, чем практически можно удовлетворить с помощью имеющихся аппаратов и жидкостей, поэтому приходится решать, какие параметры являются наиболее важными. Чтобы экспериментальное моделирование потока было полезным, оно требует от инженера достаточного опыта и суждений.

Примером, когда простого числа Рейнольдса недостаточно для подобия течений (или даже режима течения – ламинарного или турбулентного), являются ограниченные течения, т.е. течения, ограниченные стенками или другими границами. Классическим примером этого является течение Тейлора – Куэтта , где также важно безразмерное отношение радиусов ограничивающих цилиндров, и многие технические приложения, где эти различия играют важную роль. ^{[26] [27]} Принципы этих ограничений были разработаны Морисом Мари Альфредом Куэттом и Джеффри Ингрэмом Тейлором и развиты далее Флорисом Такенсом и Дэвидом Рюэлем .

Типичные значения числа Рейнольдса ^{[28] [29]}

• Диктиостелиальные амебы : ~ 1 × 10-6 ^{[ 30]}
• Бактерия ~ 1 × 10 ⁻⁴
• Инфузория ~ 1 × 10 ⁻¹
• Самая маленькая рыбка ~ 1
• Кровоток в головном мозге ~ 1 × 10 ²
• Кровоток в аорте ~ 1 × 10 ³
• Возникновение турбулентного течения от ~ 2,3×10 ³ до 5,0×10 ⁴ для трубного течения до 10 ⁶ для пограничных слоев
• Типичное поле в Высшей лиге бейсбола ~ 2 × 10 ⁵
• Купание человека ~ 4 × 10 ⁶
• Самая быстрая рыба ~ 1 × 10 ⁸
• Синий кит ~ 4 × 10 ⁸
• Большой корабль ( Королева Елизавета 2 ) ~ 5×10 ⁹
• Атмосферный тропический циклон ~ 1 х 10 ¹²

Наименьшие масштабы турбулентного движения

В турбулентном потоке существует диапазон масштабов изменяющегося во времени движения жидкости. Размер крупнейших масштабов движения жидкости (иногда называемых вихрями) определяется общей геометрией потока. Например, в промышленной дымовой трубе наибольший масштаб движения жидкости равен диаметру самой дымовой трубы. Размер наименьших чешуек задается числом Рейнольдса. По мере увеличения числа Рейнольдса становятся видны все меньшие и меньшие масштабы течения. В дымовой трубе дым может иметь множество очень малых возмущений скорости или завихрений в дополнение к большим объемным завихрениям. В этом смысле число Рейнольдса является индикатором масштабного диапазона потока. Чем выше число Рейнольдса, тем больше диапазон масштабов. Самые большие водовороты всегда будут одного и того же размера; наименьшие водовороты определяются числом Рейнольдса.

Каково объяснение этого явления? Большое число Рейнольдса указывает на то, что силы вязкости не важны при больших масштабах потока. При сильном преобладании сил инерции над силами вязкости крупнейшие масштабы движения жидкости оказываются незатухающими — вязкости недостаточно, чтобы рассеять их движения. Кинетическая энергия должна «каскадировать» от этих больших масштабов к постепенно меньшим масштабам, пока не будет достигнут уровень, для которого масштаб становится достаточно малым, чтобы вязкость стала важной (то есть силы вязкости становятся порядка инерционных). Именно на этих малых масштабах наконец происходит рассеивание энергии за счет вязкого воздействия. Число Рейнольдса указывает, в каком масштабе происходит эта вязкая диссипация.

В физиологии

Закон Пуазейля о кровообращении в организме зависит от ламинарного потока . ^[31] В турбулентном потоке скорость потока пропорциональна корню квадратному из градиента давления, в отличие от его прямой пропорциональности градиенту давления в ламинарном потоке.

Используя определение числа Рейнольдса, мы видим, что большой диаметр с быстрым потоком, где плотность крови высока, имеет тенденцию к турбулентности. Быстрые изменения диаметра сосуда могут привести к турбулентному потоку, например, когда более узкий сосуд расширяется до большего. Кроме того, выпуклость атеромы может быть причиной турбулентного потока, при котором с помощью стетоскопа можно обнаружить слышимую турбулентность.

Сложные системы

Интерпретация числа Рейнольдса была распространена на область произвольных сложных систем . Такие как финансовые потоки, ^[32] нелинейные сети, ^{[ нужна ссылка ]} и т. д. В последнем случае искусственная вязкость сводится к нелинейному механизму распределения энергии в сложных сетевых средах. Число Рейнольдса представляет собой основной параметр управления, который выражает баланс между вводимыми и рассеиваемыми потоками энергии для системы с открытой границей. Показано, что критический режим Рейнольдса разделяет два типа движения фазового пространства: ускорительный (аттрактор) и замедлительный. ^[33] Высокое число Рейнольдса приводит к хаотическому переходу режима только в рамках модели странного аттрактора .

Связь с другими безразмерными параметрами

В механике жидкости существует множество безразмерных чисел . Число Рейнольдса измеряет соотношение эффектов адвекции и диффузии на структуры в поле скорости и, следовательно, тесно связано с числами Пекле , которые измеряют соотношение этих эффектов на другие поля, переносимые потоком, например, температуру и магнитные поля. Замена кинематической вязкости ν =мкм/ρв Re из-за температуропроводности или магнитной диффузии приводит соответственно к тепловому числу Пекле и магнитному числу Рейнольдса . Таким образом, они связаны с побочными продуктами Re с коэффициентами диффузии, а именно с числом Прандтля и магнитным числом Прандтля .

Смотрите также

• Теорема Рейнольдса о переносе  - трехмерное обобщение интегрального правила Лейбница
• Коэффициент сопротивления  - безразмерный параметр для количественной оценки сопротивления жидкости.
• Отложение (геология)  - геологический процесс, при котором отложения, почва и камни добавляются к форме рельефа или массиву суши.
• Неустойчивость Кельвина – Гельмгольца

Рекомендации

Сноски

1. Определение числа Рейнольдса не следует путать с уравнением Рейнольдса или уравнением смазки.
2. Полное развитие потока происходит при входе потока в трубу, пограничный слой утолщается, а затем стабилизируется после удаления от трубы на несколько диаметров.

Цитаты

1. Тансли и Маршалл, 2001, стр. 3274–3283.
2. Стоукс 1851, стр. 8–106.
3. Зоммерфельд 1908, стр. 116–124.
4. Рейнольдс 1883, стр. 935–982.
5. Rott 1990, стр. 1–11.
6. Фалькович 2018.
7. Холл, Нэнси (5 мая 2015 г.). "Пограничный слой". Исследовательский центр Гленна . Проверено 17 сентября 2019 г.
8. "Число Рейнольдса" . Engineeringtoolbox.com . 2003.
9. Холман 2002.
10. Фокс, Макдональд и Притчард 2004, с. 348.
11. Incropera & DeWitt 1981.
12. Schlichting & Gersten 2017, стр. 416–419.
13. Холман 2002, с. 207.
14. Поттер, Виггерт и Рамадан 2012, с. 105.
15. Сешадри, К. (февраль 1978 г.). «Ламинарное течение между параллельными пластинами с впрыском реагента при высоком числе Рейнольдса». Международный журнал тепломассообмена . 21 (2): 251–253. дои : 10.1016/0017-9310(78)90230-2.
16. Стритер 1965.
17. Лиссаман 1983, стр. 223–239.
18. «Международная стандартная атмосфера». eng.cam.ac.uk. ​Проверено 17 сентября 2019 г.
19. Эренштейн и Элой 2013, стр. 321–346.
20. Родос 1989, с. 29.
21. Дюзенбери 2009, с. 49.
22. "Ямочки и перетаскивание мяча для гольфа" . Aerospaceweb.org . Проверено 11 августа 2011 г.
23. Двиведи 1977, стр. 157–165.
24. Синнотт, Коулсон и Ричардсон 2005, с. 73.
25. «Серьезная потеря напора - потеря на трение» . Атомная энергия . Проверено 17 сентября 2019 г.
26. «Ламинарный, переходный и турбулентный поток». rheologic.net . Архивировано из оригинала 17 февраля 2020 года . Проверено 17 сентября 2019 г.
27. Манневиль и Помо 2009, с. 2072.
28. Патель, Роди и Шойерер 1985, стр. 1308–1319.
29. Дюзенбери 2009, с. 136.
30. Ван, Цисюань; Отмер, Ханс Г. (01 июня 2016 г.). «Вычислительный анализ плавания амебоидов при низком числе Рейнольдса». Журнал математической биологии . 72 (7): 1893–1926. arXiv : 1509.03504 . дои : 10.1007/s00285-015-0925-9. ISSN  1432-1416. PMID  26362281. S2CID  253808496.
31. Помогает, EPW; Макдональд, Д.А. (28 июня 1954 г.). «Наблюдения за ламинарным потоком в венах». Журнал физиологии . 124 (3): 631–639. doi : 10.1113/jphysicalol.1954.sp005135. ПМК 1366298 . ПМИД  13175205. 
32. Лос 2006, с. 369.
33. Гомес Бласкес, Альберто (23 июня 2016 г.). Аэродинамический анализ плоского пола (бакалаврская работа). Политехнический университет Каталонии.

Источники

• Берд, Р. Байрон; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (2006). Транспортные явления. Джон Уайли и сыновья. ISBN 978-0-470-11539-8.
• Дюсенбери, Дэвид Б. (2009). Жизнь в микромасштабе . Кембридж, Массачусетс: Издательство Гарвардского университета. ISBN 9780674031166.
• Двиведи, ПН (1977). «Массообмен частиц и жидкости в неподвижном и псевдоожиженном слоях». Проектирование и разработка процессов промышленной и инженерной химии . 16 (2): 157–165. дои : 10.1021/i260062a001.
• Эренштейн, Уве; Элой, Кристоф (2013). «Трение кожи о движущуюся стену и его последствия для плавающих животных» (PDF) . Журнал механики жидкости . 718 : 321–346. Бибкод : 2013JFM...718..321E. дои : 10.1017/jfm.2012.613. ISSN  0022-1120. S2CID  56331294. Архивировано из оригинала (PDF) 02 марта 2019 г.
• Фалькович, Григорий (2018). Механика жидкости. Издательство Кембриджского университета. ISBN 978-1-107-12956-6.
• Фокс, RW; Макдональд, AT; Причард, Филипп Дж. (2004). Введение в механику жидкости (6-е изд.). Хобокен: Джон Уайли и сыновья. п. 348. ИСБН 978-0-471-20231-8.
• Холман, JP (2002). Теплопередача (изд. Si Units). McGraw-Hill Education (India) Pvt Limited. ISBN 978-0-07-106967-0.
• Инкропера, Фрэнк П.; ДеВитт, Дэвид П. (1981). Основы теплопередачи. Нью-Йорк: Уайли. ISBN 978-0-471-42711-7.
• Лиссаман, PBS (1983). «Профили с малым числом Рейнольдса». Анну. Преподобный Fluid Mech . 15 (15): 223–39. Бибкод : 1983AnRFM..15..223L. CiteSeerX  10.1.1.506.1131 . doi : 10.1146/annurev.fl.15.010183.001255. S2CID  123639541.
• Лос, Корнелис (2006). Риск финансового рынка: измерение и анализ. Рутледж. ISBN 978-1-134-46932-1.
• Манневиль, Пол; Помо, Ив (25 марта 2009 г.). «Переход к турбулентности». Схоларпедия . 4 (3): 2072. Бибкод : 2009SchpJ...4.2072M. doi : 10.4249/scholarpedia.2072 .
• Патель, ВК; Роди, В.; Шойерер, Г. (1985). «Модели турбулентности для пристенных потоков и потоков с низким числом Рейнольдса — обзор». Журнал АИАА . 23 (9): 1308–1319. Бибкод : 1985AIAAJ..23.1308P. дои : 10.2514/3.9086.
• Поттер, Мерл К.; Виггерт, Дэвид К.; Рамадан, Бассем Х. (2012). Механика жидкостей (4-е изд., единицы СИ). Cengage Обучение. ISBN 978-0-495-66773-5.
• Рейнольдс, Осборн (1883). «Экспериментальное исследование обстоятельств, определяющих, будет ли движение воды прямым или извилистым, и закона сопротивления в параллельных каналах». Философские труды Королевского общества . 174 : 935–982. Бибкод : 1883RSPT..174..935R. дои : 10.1098/rstl.1883.0029 . JSTOR  109431.
• Роудс, М. (1989). Введение в технологию частиц. Уайли. ISBN 978-0-471-98482-5.
• Ротт, Н. (1990). «Заметка по истории числа Рейнольдса» (PDF) . Ежегодный обзор механики жидкости . 22 (1): 1–11. Бибкод : 1990AnRFM..22....1R. doi : 10.1146/annurev.fl.22.010190.000245. S2CID  54583669. Архивировано из оригинала (PDF) 25 февраля 2019 г.
• Шлихтинг, Герман; Герстен, Клаус (2017). Теория пограничного слоя. Спрингер. ISBN 978-3-662-52919-5.
• Синнотт, РК; Коулсон, Джон Меткалф; Ричардсон, Джон Фрэнсис (2005). Химическое инженерное проектирование. Том. 6 (4-е изд.). Эльзевир Баттерворт-Хайнеманн. ISBN 978-0-7506-6538-4.
• Зоммерфельд, Арнольд (1908). «Ein Beitrag zur Hydrodynamischen Erkläerung der turbulenten Flüssigkeitsbewegüngen (Вклад в гидродинамическое объяснение турбулентных движений жидкости)» (PDF) . Международный конгресс математиков . 3 : 116–124. Архивировано из оригинала (PDF) 15 ноября 2016 г.
• Стоукс, Джордж (1851). «О влиянии внутреннего трения жидкостей на движение маятников». Труды Кембриджского философского общества . 9 :8–106. Бибкод : 1851TCaPS...9....8S.
• Стритер, Виктор Лайл (1965). Механика жидкости (3-е изд.). Нью-Йорк: МакГроу-Хилл. ОКЛК  878734937.
• Тэнсли, Клэр Э.; Маршалл, Дэвид П. (2001). «Обтекание цилиндра на плоскости с применением к разделению Гольфстрима и антарктическом циркумполярному течению» (PDF) . Журнал физической океанографии . 31 (11): 3274–3283. Бибкод : 2001JPO....31.3274T. doi :10.1175/1520-0485(2001)031<3274:FPACOA>2.0.CO;2. Архивировано из оригинала (PDF) 1 апреля 2011 г.

дальнейшее чтение

1. Бэтчелор, ГК (1967). Введение в гидродинамику . Издательство Кембриджского университета. стр. 211–215.
2. Брезина, Иржи, 1979, Распределение частиц по размерам и скорости осаждения материалов размером с песок: 2-й Европейский симпозиум по определению характеристик частиц (PARTEC), Нюрнберг, Западная Германия.
3. Брезина, Иржи, 1980, Седиментологическая интерпретация ошибок гранулометрического анализа песков; 1-е Европейское собрание Международной ассоциации седиментологов, Рурский университет в Бохуме, Федеративная Республика Германия, март 1980 г.
4. Брезина, Иржи, 1980, Распределение песка по размерам – седиментологическая интерпретация; 26-й Международный геологический конгресс, Париж , июль 1980 г., Тезисы докладов, том. 2.
5. Фоуз, Инфаз «Механика жидкости», факультет машиностроения, Оксфордский университет, 2001, с. 96
6. Хьюз, Роджер «Гидравлика в гражданском строительстве», Департамент гражданского строительства и окружающей среды, Мельбурнский университет, 1997, стр. 107–152.
7. Джерми М., «Читатель курса механики жидкости», факультет машиностроения, Кентерберийский университет, 2005 г., стр. d5.10.
8. Перселл, Э.М. «Жизнь при низком числе Рейнольдса», Американский журнал физики , том 45, стр. 3–11 (1977) [1]
9. Траски, Г.А., Юань, Ф., Кац, Д.Ф. (2004). Явления переноса в биологических системах Прентис Холл, стр. 7. ISBN 0-13-042204-5 . ISBN 978-0-13-042204-0 .  
10. Загарола М.В. и Смитс А.Дж. «Эксперименты по турбулентному потоку в трубах с высоким числом Рейнольдса». Документ AIAA № 96-0654, 34-е собрание AIAA по аэрокосмическим наукам, Рино, Невада, 15–18 января 1996 г.
11. Изобель Кларк, 1977, ROKE, компьютерная программа для нелинейного разложения смесей распределений по методу наименьших квадратов; Компьютер и геолого-геофизические науки (Pergamon Press), том. 3, с. 245 – 256.
12. BC Колби и Р.П. Кристенсен, 1957, Некоторые основы анализа размеров частиц; Гидравлическая лаборатория Сент-Энтони-Фолс, Миннеаполис, Миннесота, США, № отчета. 12 декабря, 55 страниц.
13. Артур Т. Кори, 1949, Влияние формы на скорость падения зерен песка; Диссертация магистра, Колорадский сельскохозяйственный и механический колледж, Форт-Коллинз, Колорадо, США, декабрь, 102 страницы.
14. Джозеф Р. Каррей, 1961, Отслеживание масс отложений по размерам зерен; Учеб. Интерн. Ассоциация седиментологов, Отчет о 21-й сессии Норден, Междунар. геол. Конгресс, с. 119 – 129.
15. Бургхард Уолтер Флемминг и Карен Зиглер, 1995, Модели распределения зерен по размерам и текстурные тенденции с высоким разрешением в задней барьерной среде острова Шпикерог (юг Северного моря); Сенкенбергиана Маритима, том. 26, № 1+2, с. 1 - 24.
16. Роберт Луис Фолк, 1962, «Перекосы и пески»; Жур. Осадок. Бензин., вып. 8, № 3/сентябрь, с. 105 - 111
17. ФОЛК, Роберт Луи и Уильям К. УОРД, 1957: Бар Бразос Ривер: исследование значения параметров размера зерна; Жур. Осадок. Бензин., вып. 27, № 1/Март, с. 3–26
18. Джордж Хердан, М.Л. Смит и У.Х. Хардвик (1960): Статистика малых частиц. 2-е исправленное издание, Баттервортс (Лондон, Торонто и др.), 418 стр.
19. Дуглас Инман , 1952: Меры по описанию распределения отложений по размерам. Жур. Осадок. Петрология, вып. 22, № 3/сентябрь, с. 125 - 145
20. Мирослав Йонаш, 1991: Размер, форма, состав и структура микрочастиц в результате рассеяния света; в СИВИЦКИ, Джеймс П.М., 1991, Принципы, методы и применение анализа размера частиц; Кембриджский университет. Пресс, Кембридж , 368 стр., с. 147.
21. Уильям К. Крумбейн , 1934: Частотное распределение размеров отложений; Жур. Осадок. Бензин., вып. 4, № 2/Август, с. 65 – 77.
22. Крумбейн, Уильям Кристиан и Фрэнсис Дж. Петтиджон, 1938: Руководство по осадочной петрографии; Appleton-Century-Crofts, Inc., Нью-Йорк; 549 стр.
23. Джон С. МакНаун и Пин-Нам Лин, 1952, Концентрация осадков и скорость падения; Учеб. 2-й конференции Среднего Запада. по механике жидкости, Университет штата Огайо , Колумбус, Огайо ; Государственный университет. Перепечатки Айовы по инженерному делу, Перепечатка № 109/1952, стр. 401 – 411.
24. Макнаунн, Джон С. и Дж. Малайка, 1950, Влияние формы частиц на скорость осаждения при низких числах Рейнольдса; Сделки Американского геофизического союза, том. 31, № 1/Февраль, с. 74 – 82.
25. Джерард В. Миддлтон 1967, Эксперименты по потокам плотности и мутности, III; Депонирование; Канадский журнал. наук о Земле, том. 4, с. 475–505 (определение PSI: стр. 483–485).
26. Осборн Рейнольдс , 1883: Экспериментальное исследование обстоятельств, определяющих, будет ли движение воды прямым или извилистым, а также закона сопротивления в параллельных каналах. Фил. Пер. Рой. Соц., 174, Статьи, т. 1, с. 2, с. 935 - 982
27. Э.Ф. Шульц, Р.Х. Уайльд и М.Л. Альбертсон, 1954, Влияние формы на скорость падения осадочных частиц; Колорадский сельскохозяйственный и механический колледж, Форт-Коллинз, Колорадо, Серия по отложениям MRD, № 5/июль (CER 54EFS6), 161 страница.
28. HJ Skidmore, 1948, Разработка метода стратифицированной суспензии для размерно-частотного анализа; Диссертация на кафедре механики и гидравлики государственного университета. Айова, с. 2 (? страницы).
29. Джеймс П.М. Сивицки, 1991, Принципы, методы и применение анализа размера частиц; Кембриджский университет. Пресс, Кембридж, 368 стр.

Внешние ссылки

• Число Рейнольдса - Фейнмановские лекции по физике
• Число Рейнольдса в шестидесяти символах
• Мини-биография Рейнольдса и изображение оригинального аппарата в Манчестерском университете.