Рычаг

Простая машина, состоящая из балки, вращающейся на неподвижном шарнире.

Рычаг — это простая машина, состоящая из балки или жесткого стержня, вращающегося на неподвижном шарнире , или точке опоры . Рычаг — это твердое тело, способное вращаться в точке на себе. На основе расположения точки опоры, нагрузки и усилия рычаг делится на три типа. Это одна из шести простых машин, определенных учеными эпохи Возрождения. Рычаг усиливает входную силу, чтобы обеспечить большую выходную силу, которая, как говорят, обеспечивает рычаг , который является механическим преимуществом, полученным в системе, равным отношению выходной силы к входной силе. Таким образом, рычаг является механическим устройством преимущества , уравновешивающим силу против движения.

Этимология

Слово «lever» вошло в английский язык около 1300 г. н. э. из старофранцузского : levier . Оно произошло от основы глагола lever , означающего «поднимать». Глагол, в свою очередь, восходит к латинскому : levare , ^[1] самому прилагательному levis , означающему «легкий» (как в «не тяжелый»). Первичным происхождением слова является протоиндоевропейская основа legwh- , означающая «легкий», «легкий» или «ловкий», среди прочего. Основа PIE также дала начало английскому слову «light» ^{[2] .}

История рычага

Самые ранние свидетельства существования рычажного механизма относятся к древнему Ближнему Востоку около  5000 г. до н. э. , когда он впервые был использован в простых весах . ^[3] В Древнем Египте около  4400 г. до н. э. для самого раннего горизонтального ткацкого станка использовалась ножная педаль . ^[4] В Месопотамии (современный Ирак) около  3000 г. до н. э . был изобретен шадуф — устройство, похожее на кран, в котором использовался рычажный механизм. ^[3] В Древнем Египте рабочие использовали рычаг для перемещения и подъема обелисков весом более 100 тонн. Это видно по углублениям в больших блоках и выступам для обработки , которые нельзя было использовать ни для каких целей, кроме как в качестве рычагов. ^[5]

Самые ранние сохранившиеся письменные упоминания о рычагах датируются III веком до нашей эры и, по общему мнению, принадлежат греческому математику Архимеду , который сказал: «Дайте мне рычаг достаточной длины и точку опоры, и я переверну мир».

Отем Стэнли утверждает, что палку-копалку можно считать первым рычагом, что позволяет считать доисторических женщин изобретателями рычажной технологии. ^[6]

Сила и рычаги

Рычаг в равновесии

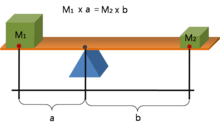
Рычаг — это балка, соединенная с землей шарниром или стержнем, называемым точкой опоры. Идеальный рычаг не рассеивает и не накапливает энергию, что означает отсутствие трения в шарнире или изгиба в балке. В этом случае мощность, входящая в рычаг, равна мощности, выходящей из него, а отношение выходной силы к входной определяется отношением расстояний от точки опоры до точек приложения этих сил. Это известно как закон рычага .

Механическое преимущество рычага можно определить, рассмотрев баланс моментов или крутящего момента , T , относительно точки опоры. Если пройденное расстояние больше, то выходная сила уменьшается.

$${\displaystyle {\begin{aligned}T_{1}&=F_{1}a,\quad \\T_{2}&=F_{2}b\!\end{aligned}}}$$

где F ₁ — входная сила на рычаге, а F ₂ — выходная сила. Расстояния a и b — перпендикулярные расстояния между силами и точкой опоры.

Поскольку моменты крутящего момента должны быть уравновешены, . Таким образом, . ${\displaystyle T_{1}=T_{2}\!}$ ${\displaystyle F_{1}a=F_{2}b\!}$

Механическое преимущество рычага — это отношение выходной силы к входной силе.

$${\displaystyle MA={\frac {F_{2}}{F_{1}}}={\frac {a}{b}}.\!}$$

Это соотношение показывает, что механическое преимущество может быть вычислено из соотношения расстояний от точки опоры до того места, где входная и выходная силы прикладываются к рычагу, предполагая, что рычаг невесомый и нет потерь из-за трения, гибкости или износа. Это остается верным, даже несмотря на то, что «горизонтальное» расстояние (перпендикулярное силе тяжести) как a, так и b изменяется (уменьшается) при изменении положения рычага в любую сторону от горизонтали.

Типы рычагов

Три класса рычагов

Три классификации рычагов с примерами человеческого тела

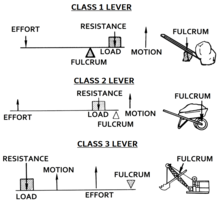
Рычаги классифицируются по относительному положению точки опоры, усилия и сопротивления (или нагрузки). Входную силу принято называть «усилием», а выходную — «нагрузкой» или «сопротивлением». Это позволяет идентифицировать три класса рычагов по относительному положению точки опоры, сопротивления и усилия: ^[7]

• Класс I – Точка опоры расположена между усилием и сопротивлением: усилие приложено с одной стороны точки опоры, а сопротивление (или нагрузка) – с другой. Например, качели , лом , ножницы , весы , плоскогубцы и молоток-гвоздодер (вытаскивающий гвоздь). При точке опоры посередине механическое преимущество рычага может быть больше, меньше или даже равно 1 .
• Класс II – Сопротивление (или нагрузка) расположено между усилием и точкой опоры: усилие приложено с одной стороны сопротивления, а точка опоры расположена с другой стороны, например , тачка , щипцы для орехов , открывалка для бутылок , гаечный ключ и педаль тормоза автомобиля. Поскольку плечо нагрузки меньше плеча усилия, механическое преимущество рычага всегда больше 1. Его также называют рычагом-множителем силы.
• Класс III – Усилие расположено между сопротивлением и точкой опоры: Сопротивление (или нагрузка) приложено с одной стороны усилия, а точка опоры расположена с другой стороны, например, пара пинцетов , молоток , пара клещей , удочка и нижняя челюсть человеческого черепа. Поскольку плечо усилия меньше плеча нагрузки, механическое преимущество рычага всегда меньше 1. Его также называют рычагом-множителем скорости.

Эти случаи описываются мнемонической формулой fre 123 , где точка опоры f находится между r и e для рычага 1-го класса, сопротивление r находится между f и e для рычага 2-го класса, а усилие e находится между f и r для рычага 3-го класса.

Составной рычаг

Составной рычаг состоит из нескольких рычагов, действующих последовательно: сопротивление одного рычага в системе рычагов действует как усилие для следующего, и таким образом приложенная сила передается от одного рычага к другому. Примерами составных рычагов являются весы, щипчики для ногтей и клавиши пианино.

Молоточек , наковальня и стремечко — это небольшие косточки в среднем ухе , соединенные как сложные рычаги, которые передают звуковые волны от барабанной перепонки к овальному окну улитки .

Закон рычага

Рычаг — это подвижная планка, которая вращается на точке опоры, прикрепленной к фиксированной точке. Рычаг работает, прикладывая силы на разных расстояниях от точки опоры или шарнира.

При вращении рычага вокруг точки опоры точки, расположенные дальше от этой точки опоры, движутся быстрее, чем точки, расположенные ближе к точке опоры. Поэтому сила, приложенная к точке, расположенной дальше от точки опоры, должна быть меньше силы, расположенной ближе к ней, поскольку мощность является произведением силы и скорости. ^[8]

Если a и b — расстояния от точки опоры до точек A и B , а сила F _A, приложенная к точке A , является входом, а сила F _B, приложенная к точке B , является выходом, то отношение скоростей точек A и B определяется как a/b , поэтому отношение выходной силы к входной силе, или механическое преимущество, определяется по формуле: $${\displaystyle MA={\frac {F_{B}}{F_{A}}}={\frac {a}{b}}.}$$

Это закон рычага , который был доказан Архимедом с помощью геометрических рассуждений. ^[9] Он показывает, что если расстояние a от точки опоры до места приложения входной силы (точка A ) больше, чем расстояние b от точки опоры до места приложения выходной силы (точка B ), то рычаг усиливает входную силу. С другой стороны, если расстояние a от точки опоры до входной силы меньше, чем расстояние b от точки опоры до выходной силы, то рычаг уменьшает входную силу.

Использование скорости в статическом анализе рычага является применением принципа виртуальной работы .

Виртуальная работа и закон рычага

Рычаг моделируется как жесткий стержень, соединенный с наземной рамой шарнирным соединением, называемым точкой опоры. Рычаг приводится в действие путем приложения входной силы F _A в точке A, расположенной по координатному вектору r _A на стержне. Затем рычаг оказывает выходную силу F _B в точке B, расположенной по координатному вектору r _B . Вращение рычага вокруг точки опоры P определяется углом поворота θ в радианах.

Рычаг Архимеда, гравюра из журнала «Mechanics Magazine» , изданного в Лондоне в 1824 году.

Пусть вектор координат точки P , определяющий точку опоры, равен r _P , и введем длины

$${\displaystyle a=|\mathbf {r} _{A}-\mathbf {r} _{P}|,\quad b=|\mathbf {r} _{B}-\mathbf {r} _{P}|,}$$

которые представляют собой расстояния от точки опоры до входной точки A и до выходной точки B соответственно.

Теперь введем единичные векторы e _A и e _B от точки опоры к точкам A и B , так что

$${\displaystyle \mathbf {r} _{A}-\mathbf {r} _{P}=a\mathbf {e} _{A},\quad \mathbf {r} _{B}-\mathbf {r} _{P}=b\mathbf {e} _{B}.}$$

Скорость точек A и B получается как

$${\displaystyle \mathbf {v} _{A}={\dot {\theta }}a\mathbf {e} _{A}^{\perp },\quad \mathbf {v} _{B}={\dot {\theta }}b\mathbf {e} _{B}^{\perp },}$$

где e _A ^⊥ и e _B ^⊥ — единичные векторы, перпендикулярные e _A и e _B соответственно.

Угол θ является обобщенной координатой , определяющей конфигурацию рычага, а обобщенная сила, связанная с этой координатой, определяется выражением

$${\displaystyle F_{\theta }=\mathbf {F} _{A}\cdot {\frac {\partial \mathbf {v} _{A}}{\partial {\dot {\theta }}}}-\mathbf {F} _{B}\cdot {\frac {\partial \mathbf {v} _{B}}{\partial {\dot {\theta }}}}=a(\mathbf {F} _{A}\cdot \mathbf {e} _{A}^{\perp })-b(\mathbf {F} _{B}\cdot \mathbf {e} _{B}^{\perp })=aF_{A}-bF_{B},}$$

где F _A и F _B — компоненты сил, перпендикулярные радиальным сегментам PA и PB . Принцип виртуальной работы гласит, что при равновесии обобщенная сила равна нулю, то есть

$${\displaystyle F_{\theta }=aF_{A}-bF_{B}=0.\,\!}$$

Простой рычаг, точка опоры и вертикальные стойки

Таким образом, отношение выходной силы F _B к входной силе F _A получается как

$${\displaystyle MA={\frac {F_{B}}{F_{A}}}={\frac {a}{b}},}$$

что является механическим преимуществом рычага.

Это уравнение показывает, что если расстояние a от точки опоры до точки A , где приложена входная сила, больше, чем расстояние b от точки опоры до точки B , где приложена выходная сила, то рычаг усиливает входную силу. Если же верно обратное, то есть расстояние от точки опоры до входной точки A меньше, чем от точки опоры до выходной точки B , то рычаг уменьшает величину входной силы.

Смотрите также

• Прикладная механика  – Практическое применение механики
• Соединение рычага баланса
• подъёмный
• Связь (механическая)  – сборка систем, соединенных для управления силами и движением.
• Механизм (техника)  – Устройство, преобразующее входные силы и движение в выходные силы и движение.
• О равновесии плоскостей  – Механический трактат Архимеда
• Простая машина  – механическое устройство, которое изменяет направление или величину силы.

Ссылки

1. Чисхолм, Хью , ред. (1911). «Рычаг»  . Encyclopaedia Britannica . Том 16 (11-е изд.). Cambridge University Press. стр. 510.
2. "Этимология слова "lever" в Online Etymological". Архивировано из оригинала 2015-05-12 . Получено 2015-04-29 .
3. Paipetis, SA; Ceccarelli, Marco (2010). Гений Архимеда — 23 века влияния на математику, науку и технику: Труды международной конференции, состоявшейся в Сиракузах, Италия, 8–10 июня 2010 г. Springer Science & Business Media . стр. 416. ISBN 9789048190911.
4. Бруно, Леонард С.; Олендорф, Донна (1997). Наука и технологии впервые . Gale Research . стр. 2. ISBN 9780787602567. 4400 г. до н.э. Самым ранним свидетельством использования горизонтального ткацкого станка является его изображение на глиняном блюде, найденном в Египте и датируемом этим временем. Эти первые настоящие рамочные ткацкие станки оснащены ножными педалями для подъема нитей основы, оставляя руки ткача свободными для пропускания и прибивания уточной нити.
5. Кларк, Сомерс; Энгельбах, Реджинальд (1990). Древнеегипетское строительство и архитектура . Courier Corporation . стр. 86–90. ISBN 9780486264851.
6. Стэнли, Осень (1983).«Женщины держат две трети неба: заметки для пересмотренной истории технологий».". В Ротшильд, Джоан (ред.). Machina Ex Dea: феминистские взгляды на технологии . Pergamon Press.
7. Давидовиц, Пол (2008). "Глава 1". Физика в биологии и медицине (3-е изд.). Academic Press. стр. 10. ISBN 978-0-12-369411-9. Архивировано из оригинала 2014-01-03 . Получено 2016-02-23 .
8. Уикер, Джон; Пеннок, Гордон; Шигли, Джозеф (2010). Теория машин и механизмов (4-е изд.). Oxford University Press USA. ISBN 978-0-19-537123-9.
9. Usher, AP (1929). История механических изобретений. Harvard University Press (перепечатано Dover Publications 1988). стр. 94. ISBN 978-0-486-14359-0. OCLC  514178. Архивировано из оригинала 26 июля 2020 г. . Получено 7 апреля 2013 г. .

Внешние ссылки

• Рычаг в энциклопедии науки и техники Diracdelta
• Простой рычаг Стивена Вольфрама , Демонстрационный проект Вольфрама .
• Рычаги: Простые машины на EnchantedLearning.com