Гравитационное ускорение

В физике гравитационное ускорение — это ускорение объекта при свободном падении в вакууме (и , таким образом, без сопротивления ). Это постоянный прирост скорости, вызванный исключительно гравитационным притяжением . Все тела ускоряются в вакууме с одинаковой скоростью, независимо от массы или состава тел; ^[1] измерение и анализ этих скоростей известны как гравиметрия .

В фиксированной точке на поверхности величина земного тяготения является результатом комбинированного эффекта гравитации и центробежной силы вращения Земли . ^[2]^[3] В разных точках на поверхности Земли ускорение свободного падения колеблется от 9,764 до 9,834 м/с ² (от 32,03 до 32,26 фут/с ² ), ^[4] в зависимости от высоты , широты и долготы . Условное стандартное значение определяется точно как 9,80665 м/с² (около 32,1740 фут/с²). Места значительного отклонения от этого значения известны как гравитационные аномалии . Это не учитывает другие эффекты, такие как плавучесть или сопротивление.

Отношение к Универсальному Закону

Закон всемирного тяготения Ньютона гласит, что между любыми двумя массами существует гравитационная сила, которая равна по величине для каждой массы и направлена так, чтобы притягивать две массы друг к другу. Формула:

F=G{\frac {m_{1}m_{2}}{r^{2}}}\

где и — любые две массы, — гравитационная постоянная , — расстояние между двумя точечными массами. $m_{1}$ $m_{2}$ $G$ $r$

Два тела, вращающиеся вокруг своего центра масс (красный крест)

Используя интегральную форму закона Гаусса , эту формулу можно распространить на любую пару объектов, один из которых намного массивнее другого — как планета относительно любого артефакта человеческого масштаба. Расстояния между планетами и между планетами и Солнцем (на много порядков) больше размеров Солнца и планет. В результате и Солнце, и планеты можно рассматривать как точечные массы , и ту же формулу можно применять к планетарным движениям. (Поскольку планеты и естественные спутники образуют пары сопоставимой массы, расстояние «r» измеряется от общих центров масс каждой пары, а не как прямое общее расстояние между центрами планет.)

Если одна масса намного больше другой, удобно взять ее в качестве наблюдаемой точки отсчета и определить ее как источник гравитационного поля, величина и ориентация которого задаются формулой: ^[5]

\mathbf {g} =-{GM \over r^{2}}\mathbf {\hat {r}}

где — масса источника поля (больше), а — единичный вектор, направленный от источника поля к массе образца (меньше). Отрицательный знак указывает на то, что сила притягивающая (направлена назад, к источнику). $М$ $\mathbf {\hat {r}}$

Тогда вектор силы притяжения к массе образца можно выразить как: $\mathbf {F}$ $м$

\mathbf {F} =m\mathbf {g}

Здесь — ускорение свободного падения без трения , поддерживаемое массой образца под действием притяжения гравитационного источника. Это вектор, направленный к источнику поля, величина которого измеряется в единицах ускорения. Вектор гравитационного ускорения зависит только от того, насколько массивен источник поля и от расстояния 'r' до массы образца . Он не зависит от величины малой массы образца. $\mathbf {г}$ $м$ $М$ $м$

Эта модель представляет собой гравитационное ускорение "дальнего поля", связанное с массивным телом. Когда размеры тела не являются тривиальными по сравнению с интересующими расстояниями, принцип суперпозиции может быть использован для дифференциальных масс для предполагаемого распределения плотности по всему телу, чтобы получить более подробную модель гравитационного ускорения "ближнего поля". Для спутников на орбите модель дальнего поля достаточна для грубых расчетов высоты в зависимости от периода , но не для точной оценки будущего местоположения после нескольких орбит.

Более подробные модели включают (помимо прочего) выпячивание на экваторе для Земли и нерегулярные концентрации массы (из-за ударов метеоров) для Луны. Миссия Gravity Recovery and Climate Experiment (GRACE), запущенная в 2002 году, состоит из двух зондов, названных «Том» и «Джерри», на полярной орбите вокруг Земли, измеряющих разницу в расстоянии между двумя зондами, чтобы более точно определить гравитационное поле вокруг Земли и отслеживать изменения, происходящие с течением времени. Аналогичным образом, миссия Gravity Recovery and Interior Laboratory с 2011 по 2012 год состояла из двух зондов («Ebb» и «Flow») на полярной орбите вокруг Луны, чтобы более точно определить гравитационное поле для будущих навигационных целей и получить информацию о физическом составе Луны.

Сравнительные гравитации Земли, Солнца, Луны и планет

В таблице ниже показаны сравнительные гравитационные ускорения на поверхности Солнца, луны Земли, каждой из планет Солнечной системы и их главных лун, Цереры, Плутона и Эриды. Для газообразных тел под «поверхностью» понимается видимая поверхность: верхние слои облаков планет- гигантов (Юпитера, Сатурна, Урана и Нептуна) и фотосфера Солнца . Значения в таблице не были снижены с учетом центробежной силы вращения планеты (и скорости ветра на верхних слоях облаков для планет-гигантов) и, следовательно, в общем случае, аналогичны фактической гравитации, которая будет ощущаться вблизи полюсов. Для справки показано время, которое потребуется объекту, чтобы упасть с высоты 100 метров, высоты небоскреба, а также максимально достигнутая скорость. Сопротивление воздуха не учитывается.

Общая теория относительности

В общей теории относительности Эйнштейна гравитация является атрибутом искривленного пространства-времени, а не возникает из-за силы, распространяющейся между телами. В теории Эйнштейна массы искажают пространство-время в своей окрестности, а другие частицы движутся по траекториям, определяемым геометрией пространства-времени. Гравитационная сила является фиктивной силой . Гравитационного ускорения не существует, поскольку собственное ускорение и, следовательно, 4-ускорение объектов в свободном падении равны нулю. Вместо того чтобы испытывать ускорение, объекты в свободном падении движутся по прямым линиям ( геодезическим ) в искривленном пространстве-времени.

Гравитационное поле

Изображение гравитационного поля Земли и Луны вместе (не в масштабе). Вектор поля (синее) и связанное с ним скалярное потенциальное поле (красное). Точка P между Землей и Луной является точкой равновесия .

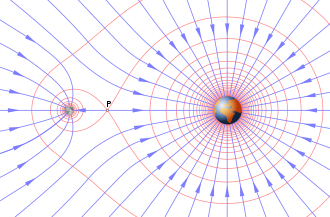
В физике гравитационное поле или поле гравитационного ускорения — это векторное поле, используемое для объяснения влияний, которые тело оказывает в пространстве вокруг себя. ^[6] Гравитационное поле используется для объяснения гравитационных явлений, таких как поле гравитационной силы, оказываемое на другое массивное тело. Оно имеет размерность ускорения (L/T ² ) и измеряется в единицах ньютонов на килограмм (Н/кг) или, что эквивалентно, в метрах в секунду в квадрате (м/с ² ).

В своей первоначальной концепции гравитация была силой между точечными массами . Вслед за Исааком Ньютоном Пьер -Симон Лаплас попытался смоделировать гравитацию как некий вид поля излучения или жидкости , ^{[ необходима ссылка ]} и с 19-го века объяснения гравитации в классической механике обычно преподавались в терминах полевой модели, а не точечного притяжения. Она возникает из-за пространственного градиента поля гравитационного потенциала .

В общей теории относительности , вместо того, чтобы две частицы притягивались друг к другу, частицы искажают пространство-время посредством своей массы, и это искажение воспринимается и измеряется как «сила». ^{[ необходима ссылка ]} В такой модели утверждается, что материя движется определенным образом в ответ на кривизну пространства-времени, ^[7] и что либо нет никакой гравитационной силы , ^[8] либо гравитация является фиктивной силой . ^[9]

Гравитация отличается от других сил тем, что подчиняется принципу эквивалентности .

Смотрите также

Примечания

^ Это значение не учитывает поправку на центробежную силу, обусловленную вращением Земли, и поэтому превышает значение стандартной силы тяжести 9,80665 м/с ² .

Ссылки

^ Джеральд Джеймс Холтон и Стивен Г. Браш (2001). Физика, человеческое приключение: от Коперника до Эйнштейна и далее (3-е изд.). Rutgers University Press . стр. 113. ISBN 978-0-8135-2908-0.
^ Boynton, Richard (2001). "Точное измерение массы" (PDF) . Sawe Paper No. 3147 . Arlington, Texas: SAWE, Inc. Архивировано из оригинала (PDF) 2007-02-27 . Получено 2007-01-21 .
^ Хофманн-Велленхоф, Б.; Мориц, Х. (2006). Физическая геодезия (2-е изд.). Springer. ISBN 978-3-211-33544-4§ 2.1: «Полная сила, действующая на тело, покоящееся на поверхности Земли, является равнодействующей силы тяготения и центробежной силы вращения Земли и называется силой тяжести».{{cite book}}: CS1 maint: постскриптум ( ссылка )
^ Hirt, C.; Claessens, S.; Fecher, T.; Kuhn, M.; Pail, R.; Rexer, M. (2013). «Новая сверхвысокоразрешающая картина гравитационного поля Земли». Geophysical Research Letters . 40 (16): 4279–4283. Bibcode : 2013GeoRL..40.4279H. doi : 10.1002/grl.50838 . hdl : 20.500.11937/46786 .
^ Фредрик Дж. Буче (1975). Введение в физику для ученых и инженеров, 2-е изд . США: Фон Хоффманн Пресс. ISBN 978-0-07-008836-8.
^ Фейнман, Ричард (1970). Лекции Фейнмана по физике. Том I. Эддисон Уэсли Лонгман. ISBN 978-0-201-02115-8.
^ Герох, Роберт (1981). Общая теория относительности от А до В. Издательство Чикагского университета . стр. 181. ISBN 978-0-226-28864-2.
^ Грён, Эйвинд; Хервик, Сигбьёрн (2007). Общая теория относительности Эйнштейна: с современными приложениями в космологии. Спрингер Япония. п. 256. ИСБН 978-0-387-69199-2.
^ Фостер, Дж.; Найтингейл, Дж. Д. (2006). Краткий курс общей теории относительности (3-е изд.). Springer Science & Business. стр. 55. ISBN 978-0-387-26078-5.