

Калькулятор Паскаля (также известный как арифметическая машина или Паскалина ) — механический калькулятор, изобретенный Блезом Паскалем в 1642 году. К разработке калькулятора Паскаля подтолкнули трудоемкие арифметические вычисления, необходимые для работы его отца в качестве налогового инспектора в Руане . [2] Он спроектировал машину для непосредственного сложения и вычитания двух чисел, а также для выполнения умножения и деления посредством многократного сложения или вычитания.
Калькулятор Паскаля был особенно успешен в конструкции своего механизма переноса, который добавляет 1 к 9 на одном циферблате и переносит 1 на следующий циферблат, когда первый циферблат меняется с 9 на 0. Его нововведение сделало каждую цифру независимой от состояния других, что позволило нескольким переносам быстро переходить от одной цифры к другой независимо от емкости машины. Паскаль также был первым, кто уменьшил и приспособил для своей цели фонарную шестерню , используемую в башенных часах и водяных колесах . Это нововведение позволило устройству выдерживать силу любого ввода оператора с очень небольшим дополнительным трением.
Паскаль спроектировал машину в 1642 году. [3] После 50 прототипов он представил устройство публике в 1645 году, посвятив его Пьеру Сегье , тогдашнему канцлеру Франции . [4] Паскаль построил около двадцати еще машин в течение следующего десятилетия, многие из которых улучшили его первоначальный дизайн. В 1649 году король Франции Людовик XIV предоставил Паскалю королевскую привилегию (похожую на патент ), которая предоставляла исключительное право проектировать и производить вычислительные машины во Франции. В настоящее время существует девять калькуляторов Паскаля; [5] большинство из них выставлены в европейских музеях.
Многие более поздние калькуляторы были либо напрямую вдохновлены, либо сформированы теми же историческими влияниями, которые привели к изобретению Паскаля. Готфрид Лейбниц изобрел свои колеса Лейбница после 1671 года, после попытки добавить функцию автоматического умножения к Паскалине. [6] В 1820 году Томас де Кольмар спроектировал свой арифмометр , первый механический калькулятор, достаточно прочный и надежный, чтобы его можно было использовать ежедневно в офисной среде. Неясно, видел ли он когда-либо устройство Лейбница, но он либо заново изобрел его, либо использовал изобретение Лейбница — шаговый барабан.

Блез Паскаль начал работать над своим калькулятором в 1642 году, когда ему было 18 лет. Он помогал отцу, работавшему налоговым комиссаром, и пытался создать устройство, которое могло бы уменьшить часть его рабочей нагрузки. В 1649 году Паскаль получил королевскую привилегию , которая давала ему исключительные права на производство и продажу счетных машин во Франции.
К 1654 году он продал около двадцати машин (из этих двадцати машин, как известно, существуют только девять [7] ), но стоимость и сложность Pascaline стали препятствием для дальнейших продаж, и производство прекратилось в том же году. К тому времени Паскаль перешел к изучению религии и философии , что дало нам и Lettres provinciales , и Pensées .
Трехсотлетие изобретения Паскалем механического калькулятора пришлось на время Второй мировой войны , когда Франция была оккупирована Германией, и поэтому главное празднование состоялось в Лондоне, Англия. Речи, произнесенные во время мероприятия, подчеркивали практические достижения Паскаля, когда он уже был известен в области чистой математики, и его творческое воображение, а также то, насколько опередили свое время и машина, и ее изобретатель. [8]


Калькулятор имел металлические колесные циферблаты со спицами, на которых по окружности каждого колеса отображались цифры от 0 до 9. Чтобы ввести цифру, пользователь помещал стилус в соответствующее пространство между спицами и поворачивал циферблат до тех пор, пока не достигал металлического упора внизу, подобно тому, как используется поворотный диск телефона. Это отображало число в окошках в верхней части калькулятора. Затем нужно было просто повторно набрать второе число, которое нужно было сложить, в результате чего сумма обоих чисел появлялась в аккумуляторе.
Каждый циферблат связан с однозначным окном дисплея, расположенным прямо над ним, которое отображает значение аккумулятора для этой позиции. Дополнение этой цифры в основании колеса (6, 10, 12, 20) отображается прямо над этой цифрой. Горизонтальная полоса скрывает либо все дополнительные числа, когда она сдвинута наверх, либо все прямые числа, когда она сдвинута к центру машины. Таким образом, она отображает либо содержимое аккумулятора, либо дополнение его значения.
Так как шестеренки калькулятора вращались только в одном направлении, отрицательные числа нельзя было напрямую суммировать. Для вычитания одного числа из другого использовался метод девятого дополнения. Единственные два различия между сложением и вычитанием — это положение полосы дисплея (прямое против дополнительного) и способ ввода первого числа (прямое против дополнительного).
Для 10-значного колеса (N) фиксированное внешнее колесо пронумеровано от 0 до 9 (N-1). Цифры вписаны в порядке убывания по часовой стрелке, начиная с нижнего левого угла до нижнего правого угла стопорного рычага. Чтобы добавить 5, нужно вставить стилус между спицами, которые окружают цифру 5, и повернуть колесо по часовой стрелке до упора. Число, отображаемое на соответствующем регистре дисплея, увеличится на 5, и, если произойдет перенос, регистр дисплея слева от него увеличится на 1. Чтобы добавить 50, используйте колесо ввода десятков (второй циферблат справа на десятичной машине), чтобы добавить 500, используйте колесо ввода сотен и т. д.
На всех колесах всех известных машин, за исключением машины tardive , [9] отмечены две соседние спицы; эти отметки различаются от машины к машине. На колесе, изображенном справа, это просверленные точки, на геодезической машине они вырезаны; некоторые просто царапины или отметки, сделанные небольшим количеством лака, [10] некоторые были даже отмечены маленькими кусочками бумаги. [11]
Эти отметки используются для установки соответствующего цилиндра на его максимальный номер, готовый к повторному обнулению. Для этого оператор вставляет стилус между этими двумя спицами и поворачивает колесо до упора в стопорный рычаг. Это работает, потому что каждое колесо напрямую связано с соответствующим ему цилиндром отображения (оно автоматически поворачивается на один во время операции переноса). Чтобы пометить спицы во время производства, можно переместить цилиндр так, чтобы отображался его максимальный номер, а затем пометить спицу под стопорным рычагом и спицу справа от него.
Четыре из известных машин имеют внутренние колеса дополнений, которые использовались для ввода первого операнда при вычитании. Они установлены в центре каждого металлического колеса со спицами и вращаются вместе с ним. Колесо, показанное на рисунке выше, имеет внутреннее колесо дополнений, но написанные на нем числа едва видны. На десятичной машине цифры от 0 до 9 вырезаны по часовой стрелке, причем каждая цифра расположена между двумя спицами, так что оператор может напрямую вписать ее значение в окно дополнений, поместив свой стилус между ними и повернув колесо по часовой стрелке до упора. [12] Метки на двух соседних спицах обрамляют цифру 0, написанную на этом колесе.
На четырех известных машинах над каждым колесом на панели дисплея установлено небольшое колесо частного. Эти колеса частного, которые устанавливаются оператором, имеют числа от 1 до 10, вписанные по часовой стрелке на их периферии (даже над недесятичным колесом). Колеса частного, по-видимому, использовались во время деления для запоминания количества раз, которое делитель был вычтен при каждом заданном индексе. [13]


Паскаль перебрал 50 прототипов, прежде чем остановиться на своем окончательном проекте; мы знаем, что он начал с какого-то счетного часового механизма, который, по-видимому, «работает на пружинах и имеет очень простую конструкцию», использовался «много раз» и оставался в «рабочем состоянии». Тем не менее, «постоянно совершенствуя его», он нашел причину попытаться сделать всю систему более надежной и прочной. [14] В конце концов он принял компонент очень больших часов, уменьшив и адаптировав для своей цели прочные шестерни, которые можно найти в механизме башенных часов, называемом фонарной шестерней , которая сама по себе произошла от механизма водяного колеса. Это могло легко выдерживать силу ввода оператора. [15]
Паскаль адаптировал механизм собачки и храповика к своей собственной конструкции колеса башенного типа; собачка не дает колесу вращаться против часовой стрелки во время ввода данных оператором, но она также используется для точного позиционирования колеса дисплея и механизма переноса для следующей цифры, когда оно выталкивается вверх и попадает в следующую позицию. Благодаря этому механизму каждое отображаемое число идеально центрируется в окне дисплея, и каждая цифра точно позиционирована для следующей операции. Этот механизм будет перемещаться шесть раз, если оператор наберет шесть на соответствующем колесе ввода.

Сотуар является центральной частью механизма переноса паскалины. В своем "Avis nécessaire..." Паскаль отметил, что машина с 10 000 колес будет работать так же хорошо, как и машина с двумя колесами, потому что каждое колесо независимо от другого. Когда приходит время распространить перенос, сотуар под действием только силы тяжести [16] бросается к следующему колесу без какого-либо контакта между колесами. Во время своего свободного падения сотуар ведет себя как акробат, прыгающий с одной трапеции на другую, при этом трапеции не касаются друг друга ("sautoir" происходит от французского глагола sauter , что означает прыгать). Поэтому все колеса (включая шестерни и сотуар) имеют одинаковый размер и вес независимо от мощности машины.
Паскаль использовал гравитацию для вооружения сотуаров. Чтобы полностью вооружить сотуар, нужно повернуть колесо на пять шагов от 4 до 9, но перенос переместит следующее колесо только на один шаг. Таким образом, во время вооружения сотуара накапливается много дополнительной энергии.
Все сотуары активируются либо операторским вводом, либо переносом вперед. Чтобы переустановить 10000-колесную машину, если бы таковая существовала, оператору пришлось бы установить каждое колесо на максимум, а затем добавить 1 к колесу «единицы». Перенос поворачивал бы каждое входное колесо одно за другим в очень быстрой манере эффекта домино , и все регистры дисплея были бы сброшены.
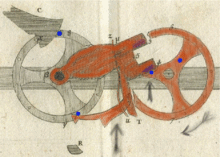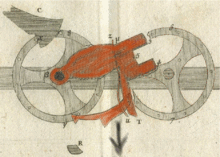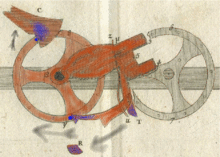
Передача сигнала осуществляется в три фазы:
Pascaline — это прямая арифмометрическая машина (не имеет рукоятки), поэтому значение числа добавляется к аккумулятору по мере его набора. Перемещая полосу дисплея, оператор может видеть либо число, хранящееся в калькуляторе, либо дополнение его значения. Вычитания выполняются так же, как и сложения, с использованием некоторых свойств арифметики дополнения до 9.
Дополнение до 9 любого однозначного десятичного числа d равно 9- d . Таким образом, дополнение до 9 числа 4 равно 5, а дополнение до 9 числа 9 равно 0. Аналогично, дополнение до 11 числа 3 равно 8.
В десятичной машине с n циферблатами дополнение числа A до 9 равно:
и, следовательно, дополнение до 9 числа (AB) равно:
Другими словами, дополнение до 9 разности двух чисел равно сумме дополнений до 9 уменьшаемого, добавленного к вычитаемому. Тот же принцип действителен и может быть использован с числами, составленными из цифр с различными основаниями (основание 6, 12, 20), как в геодезических или счетных машинах.
Это также может быть расширено до:
Этот принцип применим к Паскалине:
Машину необходимо переустанавливать на ноль перед каждой новой операцией. Чтобы переустановить машину, оператор должен установить все колеса на максимум, используя отметки на двух соседних спицах, а затем добавить 1 к самому правому колесу. [17]
Метод повторного обнуления, выбранный Паскалем, который распространяет перенос прямо через машину, является самой сложной задачей для механического калькулятора и доказывает перед каждой операцией, что машина полностью функциональна. Это является свидетельством качества Pascaline, поскольку ни одна из критических замечаний 18-го века в адрес машины не упоминала о проблеме с механизмом переноса, и тем не менее эта функция была полностью проверена на всех машинах, их сбросами, все время. [18]
Сложения выполняются с помощью индикаторной панели, перемещенной ближе к краю машины, показывающей непосредственное значение аккумулятора.
После повторной установки нуля на аппарате набираются цифры одна за другой.
В следующей таблице показаны все шаги, необходимые для вычисления 12 345 + 56 789 = 69 134.
Вычитание выполняется с помощью индикаторной полосы, перемещенной ближе к центру машины, показывающей дополнительное значение аккумулятора.
Аккумулятор содержит во время первого шага и после добавления B. При отображении этих данных в окне дополнения оператор видит , которое является A, а затем , которое является . Это похоже на сложение, поскольку единственные два различия между сложением и вычитанием — это положение полосы отображения (прямое против дополнительного) и способ ввода первого числа (прямое против дополнительного).
В следующей таблице показаны все шаги, необходимые для вычисления 54,321-12,345=41,976.
Паскалины выпускались как в десятичном , так и в недесятичном исполнении, и обе эти разновидности можно увидеть в музеях сегодня. Они были разработаны для использования учеными, бухгалтерами и геодезистами. Простейшая Паскалина имела пять циферблатов; более поздние варианты имели до десяти циферблатов.
Современная французская денежная система использовала ливы , соли и денье, в одном ливре было 20 солей , а в одном соль — 12 денье . Длина измерялась в туазах , пье , пуасах и линях , в туазе было 6 пье , в пье — 12 пуасов , в пуасе — 12 линей . Поэтому для паскалины требовались колеса с основанием 6, 10, 12 и 20. Недесятичные колеса всегда располагались перед десятичной частью.
В счетной машине (..10,10,20,12) десятичная часть считала количество ливров (20 солей ), солей (12 денье ) и денье . В землемерной машине (..10,10,6,12,12) десятичная часть считала количество туазов (6 пье ), пье (12 пусов ), пусов (12 линий ) и линий . Научные машины имели только десятичные колеса.
Десятичная часть каждой машины выделена.
Метрическая система была принята во Франции 10 декабря 1799 года, и к тому времени базовая конструкция Паскаля вдохновила других мастеров, хотя и не имела коммерческого успеха.
Большинство машин, переживших столетия, относятся к типу бухгалтерских. Семь из них находятся в европейских музеях, одна принадлежит корпорации IBM, а одна находится в частных руках.

Паскаль планировал широко распространять Pascaline, чтобы уменьшить нагрузку на людей, которым нужно было выполнять трудоемкие арифметические действия. [24] Черпая вдохновение у своего отца, налогового комиссара , Паскаль надеялся сократить часы вычислений, выполняемых работниками таких профессий, как математика, физика, астрономия и т. д. [25] Но из-за сложности устройства, отношений Паскаля с мастерами и законов об интеллектуальной собственности, на которые он влиял, производство Pascaline было гораздо более ограниченным, чем он предполагал. За 10 лет после его создания было выпущено всего 20 Pascaline. [26]
В 1649 году король Франции Людовик XIV предоставил Паскалю королевскую привилегию (предшественник патента ) , которая предоставляла исключительное право на проектирование и производство вычислительных машин во Франции, что позволило Pascaline стать первым калькулятором, проданным дистрибьютором. [27] Паскаль опасался, что мастера не смогут точно воспроизвести его Pascaline, что приведет к появлению поддельных копий, которые погубят его репутацию вместе с репутацией его машины. [24] В 1645 году, чтобы контролировать производство своего изобретения, Паскаль написал монсеньору Ле Шанселье (канцлеру Франции Пьеру Сегье ) в своем письме под названием «La Machine d'arithmétique. Lettre dédicatoire à Monseigneur le Chancelier». [24] Паскаль просил, чтобы ни одна Pascaline не производилась без его разрешения. [24] Его изобретательность снискала уважение короля Франции Людовика XIV , который удовлетворил его просьбу, но за это пришлось заплатить высокую цену: мастера не могли законно экспериментировать с конструкцией Паскаля, и они не могли распространять его машину без его разрешения/руководства.
Паскаль жил во Франции во времена Старого режима . В его время ремесленники в Европе все чаще организовывались в гильдии , например, английские часовщики, которые основали гильдию часовщиков в 1631 году, на полпути к усилиям Паскаля по созданию калькулятора. Это повлияло на способность Паскаля набирать таланты, поскольку гильдии часто сокращали обмен идеями и торговлю; иногда ремесленники вообще отказывались от своего труда, чтобы восстать против дворян. Таким образом, Паскаль оказался на рынке, где не хватало навыков и желающих рабочих. [28] Важно то, что ремесленники не были свободны как интеллектуалы, чтобы создать машину: Готфрид Лейбниц , который построил калькулятор Паскаля позже в 17 веке, остановил прогресс для своей машины из-за того, что его ремесленник продавал детали машины для финансовой платежеспособности. [29]
Поведение самого Паскаля привело к трудностям в наборе мастеров для его проекта. Это было обусловлено его убеждением, что вопросы разума важнее вопросов тела. Паскаль был не одинок, так как многие натурфилософы его времени имели гилеморфное понимание процесса изобретения: идеи предшествуют материализации, как форма предшествует материи. Это, естественно, привело к акценту на теоретической чистоте и недооценке практической работы. Как Паскаль описывал мастеров: «[они] работают путем проб и ошибок, то есть без определенных мер и пропорций, регулируемых искусством, не производя ничего, соответствующего тому, что они искали, или, что еще хуже, они создают маленького монстра, у которого отсутствуют его основные конечности, а другие деформированы, лишены какой-либо пропорции». [30]

Паскаль управлял своим проектом, имея в виду эту иерархию: он изобретал и думал, в то время как ремесленники просто исполняли. Он скрывал теорию от ремесленников, вместо этого продвигая идею о том, что они должны просто помнить, что делать, а не обязательно почему они должны это делать, т. е. до тех пор, пока «практика не сделает правила теории настолько общими, что [правила] наконец будут сведены к искусству». Это проистекало из его неверия не только в процесс ремесленного труда, но и в самих ремесленников: «ремесленники не могут регулировать себя, чтобы производить унифицированные машины автономно». [30]
Напротив, Сэмюэл Морланд , один из современников Паскаля, также работавший над созданием вычислительной машины, вероятно, добился успеха благодаря своей способности поддерживать хорошие отношения со своими мастерами. Морланд с гордостью приписывал часть своего изобретения мастерам по имени — странное дело для дворянина по отношению к простолюдину в то время. Морланд смог набрать лучших талантов в Европе. Его первым мастером был знаменитый Питер Блондо , который уже получил защиту и признание от французского государственного деятеля Ришелье за свой вклад в производство монет для Англии. Другие мастера Морланда были такими же успешными: третий, голландец Джон Фромантил , происходил из известной голландской семьи, которая изобрела маятниковые часы. [30]
В конце концов, Паскалю удалось закрепить за собой имя единственного создателя Pascaline. В королевском патенте указано, что это было его изобретение. [31]


Помимо того, что паскалина была первой вычислительной машиной, представленной публике в свое время, она также:
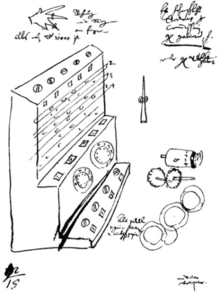
В 1957 году Франц Хаммер, биограф Иоганна Кеплера , объявил об обнаружении двух писем, которые Вильгельм Шиккард написал своему другу Иоганну Кеплеру в 1623 и 1624 годах, которые содержат чертежи ранее неизвестных работающих счетных часов, предшествовавших работе Паскаля на двадцать лет. [36] В письме 1624 года говорилось, что первая машина, построенная профессионалом, была уничтожена в пожаре во время ее строительства, и что он отказывается от своего проекта. [37] После тщательного изучения было обнаружено, вопреки пониманию Франца Хаммера, что чертежи Шиккарда публиковались по крайней мере один раз в столетие, начиная с 1718 года . [38]
Бруно фон Фрейтаг Лорингхофф, профессор математики в Тюбингенском университете, построил первую копию машины Шиккарда, но не без добавления колес и пружин для завершения конструкции. [39] Эта деталь не описана в двух сохранившихся письмах и чертежах Шиккарда. Проблема в работе машины Шиккарда, основанная на сохранившихся заметках, была обнаружена после того, как копии были построены. [40] Машина Шиккарда использовала часовые колеса, которые были сделаны более прочными и, следовательно, более тяжелыми, чтобы предотвратить их повреждение силой ввода оператора. Каждая цифра использовала колесо отображения, колесо ввода и промежуточное колесо. Во время переноса все эти колеса сцеплялись с колесами цифры, принимающей перенос. Кумулятивное трение и инерция всех этих колес могли «...потенциально повредить машину, если перенос должен был распространяться через цифры, например, как добавление 1 к числу, такому как 9999». [41] Величайшим новшеством в калькуляторе Паскаля было то, что он был спроектирован таким образом, что каждое входное колесо было полностью независимо от всех остальных, а переносы распространялись последовательно. Паскаль выбрал для своей машины метод повторного обнуления, который распространял перенос прямо через машину. [17] Это самая требовательная операция для выполнения для механического калькулятора и доказывал, перед каждой операцией, что механизм переноса Паскалина был полностью функционален. Это можно было бы считать свидетельством качества Паскалина, потому что ни одна из критических замечаний 18-го века в адрес машины не упоминала проблемы с механизмом переноса, и тем не менее эта функция была полностью проверена на всех машинах, их сбросами, все время. [18]

Готфрид Лейбниц начал работать над собственным калькулятором после смерти Паскаля. Сначала он попытался построить машину, которая могла бы автоматически умножать, сидя на калькуляторе Паскаля, ошибочно предположив, что все циферблаты на калькуляторе Паскаля могут работать одновременно. Хотя это и невозможно было сделать, это был первый случай, когда вертушка была описана и использована в чертеже калькулятора.
Затем он разработал конкурирующий проект, Stepped Reckoner , который должен был автоматически выполнять сложения, вычитания и умножения, а также деление под контролем оператора. Лейбниц боролся в течение сорока лет, чтобы усовершенствовать этот проект, и создал две машины, одну в 1694 и одну в 1706. [42] Известно, что существует только машина, построенная в 1694; она была вновь обнаружена в конце 19-го века, проведя 250 лет забытой на чердаке в Геттингенском университете . [42]
Немецкому изобретателю счетной машины Артуру Буркхардту было поручено попытаться привести машину Лейбница в рабочее состояние. Его отчет был благоприятным, за исключением последовательности в переносе. [43] и «поэтому, особенно в случае множественных переносов, оператор должен был проверить результат и вручную исправить возможные ошибки». [44] Лейбницу не удалось создать калькулятор, который работал бы должным образом, но он изобрел колесо Лейбница , принцип двухдвижущегося механического калькулятора. Он также был первым, у кого были курсоры для записи первого операнда и подвижная каретка для результатов.
В XVII веке было предпринято еще пять попыток создания счетных машин с «прямым вводом» (включая разработки Тито Бураттини , Сэмюэля Морланда и Рене Грийе ).
Около 1660 года Клод Перро спроектировал абак рабдологический , который часто ошибочно принимают за механический калькулятор, поскольку у него есть механизм переноса между числами. Но на самом деле это абак, поскольку он требует от оператора особого обращения с машиной, когда происходит перенос. [45]
Калькулятор Паскаля был самым успешным механическим калькулятором, разработанным в 17 веке для сложения и вычитания больших чисел. У ступенчатого счетчика возникали проблемы с механизмом переноса после более чем двух последовательных переносов, а другие устройства имели механизмы переноса (однозубое колесо), которые были ограничены в своей способности переносить через несколько цифр или не имели механизма переноса между цифрами аккумулятора.
Счетные машины не были коммерчески жизнеспособными до 1851 года, когда Томас де Кольмар выпустил, после тридцати лет разработки, свой упрощенный арифмометр , первую машину, достаточно мощную для ежедневного использования в офисной среде. Арифмометр был разработан на основе колес Лейбница и изначально использовал метод дополнения до 9 Паскаля для вычитания.