RC-цепь

Электрическая цепь, состоящая из резисторов и конденсаторов

Резисторно -емкостная цепь ( RC-цепь ), или RC-фильтр или RC-сеть — это электрическая цепь, состоящая из резисторов и конденсаторов . Она может управляться источником напряжения или тока , и они будут вызывать различные реакции. RC-цепь первого порядка состоит из одного резистора и одного конденсатора и является простейшим типом RC-цепи.

RC-цепи могут использоваться для фильтрации сигнала путем блокирования определенных частот и пропускания других. Два наиболее распространенных RC-фильтра — это фильтры верхних частот и фильтры нижних частот ; полосовые фильтры и полосовые заграждающие фильтры обычно требуют RLC-фильтров , хотя грубые фильтры можно сделать с помощью RC-фильтров.

Введение

Существует три основных линейных пассивных сосредоточенных аналоговых компонента схемы: резистор (R), конденсатор (C) и катушка индуктивности (L). Они могут быть объединены в RC-цепь, RL-цепь , LC-цепь и RLC-цепь , с аббревиатурами, указывающими, какие компоненты используются. Эти схемы, среди прочего, демонстрируют большое количество важных типов поведения, которые являются основополагающими для большей части аналоговой электроники . В частности, они могут действовать как пассивные фильтры . В этой статье рассматривается RC-цепь как в последовательной , так и в параллельной формах, как показано на схемах ниже.

Естественная реакция

RC-цепь

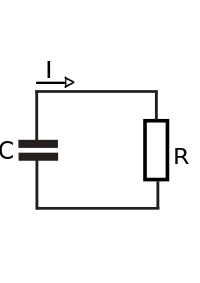
Простейшая RC-цепь состоит из резистора и заряженного конденсатора, соединенных друг с другом в один контур, без внешнего источника напряжения. После замыкания цепи конденсатор начинает разряжать свою накопленную энергию через резистор. Напряжение на конденсаторе, которое зависит от времени, можно найти, используя закон Кирхгофа для токов . Ток через резистор должен быть равен по величине (но противоположен по знаку) производной по времени накопленного заряда на конденсаторе. Это приводит к линейному дифференциальному уравнению

${\displaystyle C{\frac {dV}{dt}}+{\frac {V}{R}}=0\,,}$

где С — емкость конденсатора.

Решение этого уравнения относительно V дает формулу для экспоненциального затухания :

${\displaystyle V(t)=V_{0}e^{-{\frac {t}{RC}}}\,,}$

где V ₀ — напряжение конденсатора в момент времени t = 0 .

Время, необходимое для падения напряжения до ⁠В ₀/е⁠ называется постоянной времени RC и определяется как ^[1]

${\displaystyle \tau =RC\,.}$

В этой формуле τ измеряется в секундах, R в омах, а C в фарадах.

Комплексное сопротивление

Комплексное сопротивление Z _C (в Омах ) конденсатора емкостью C (в фарадах ) равно

${\displaystyle Z_{C}={\frac {1}{sC}}}$

Комплексная частота s , в общем случае, является комплексным числом ,

${\displaystyle s=\sigma +j\omega \,,}$

где

• j представляет мнимую единицу : j ² = −1 ,
• σ — константа экспоненциального спада (в неперах в секунду), а
• ω — синусоидальная угловая частота (в радианах в секунду ).

Синусоидальное устойчивое состояние

Синусоидальное устойчивое состояние является особым случаем, в котором входное напряжение представляет собой чистую синусоиду (без экспоненциального затухания). В результате и импеданс становится ${\displaystyle \sigma =0}$

${\displaystyle Z_{C}={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}\,.}$

Последовательная цепь

Последовательная RC-цепь

Рассматривая цепь как делитель напряжения , напряжение на конденсаторе равно:

${\displaystyle V_{C}(s)={\frac {\frac {1}{Cs}}{R+{\frac {1}{Cs}}}}V_{\mathrm {in} }(s)={\frac {1}{1+RCs}}V_{\mathrm {in} }(s)}$

а напряжение на резисторе равно:

${\displaystyle V_{R}(s)={\frac {R}{R+{\frac {1}{Cs}}}}V_{\mathrm {in} }(s)={\frac {RCs}{1+RCs}}V_{\mathrm {in} }(s)\,.}$

Передаточные функции

Передаточная функция от входного напряжения к напряжению на конденсаторе равна

${\displaystyle H_{C}(s)={\frac {V_{C}(s)}{V_{\mathrm {in} }(s)}}={\frac {1}{1+RCs}}\,.}$

Аналогично, передаточная функция от входа к напряжению на резисторе равна

${\displaystyle H_{R}(s)={\frac {V_{R}(s)}{V_{\rm {in}}(s)}}={\frac {RCs}{1+RCs}}\,.}$

Полюса и нули

Обе передаточные функции имеют один полюс, расположенный в

${\displaystyle s=-{\frac {1}{RC}}\,.}$

Кроме того, передаточная функция для напряжения на резисторе имеет ноль , расположенный в начале координат .

Усиление и фаза

Амплитудная и фазовая передаточные функции для последовательной RC-цепи

Величина прироста по двум компонентам составляет

${\displaystyle G_{C}={\big |}H_{C}(j\omega ){\big |}=\left|{\frac {V_{C}(j\omega )}{V_{\mathrm {in} }(j\omega )}}\right|={\frac {1}{\sqrt {1+\left(\omega RC\right)^{2}}}}}$

и

${\displaystyle G_{R}={\big |}H_{R}(j\omega ){\big |}=\left|{\frac {V_{R}(j\omega )}{V_{\mathrm {in} }(j\omega )}}\right|={\frac {\omega RC}{\sqrt {1+\left(\omega RC\right)^{2}}}}\,,}$

и фазовые углы равны

${\displaystyle \phi _{C}=\angle H_{C}(j\omega )=\tan ^{-1}\left(-\omega RC\right)}$

и

${\displaystyle \phi _{R}=\angle H_{R}(j\omega )=\tan ^{-1}\left({\frac {1}{\omega RC}}\right)\,.}$

Эти выражения вместе можно подставить в обычное выражение для вектора, представляющего выход:

${\displaystyle {\begin{aligned}V_{C}&=G_{C}V_{\mathrm {in} }e^{j\phi _{C}}\\V_{R}&=G_{R}V_{\mathrm {in} }e^{j\phi _{R}}\,.\end{aligned}}}$

Текущий

Ток в цепи везде одинаков, так как цепь последовательная:

${\displaystyle I(s)={\frac {V_{\mathrm {in} }(s)}{R+{\frac {1}{Cs}}}}={\frac {Cs}{1+RCs}}V_{\mathrm {in} }(s)\,.}$

Импульсный ответ

Импульсная характеристика последовательной RC-цепи

Импульсная характеристика для каждого напряжения является обратным преобразованием Лапласа соответствующей передаточной функции. Она представляет собой реакцию схемы на входное напряжение, состоящее из импульса или дельта-функции Дирака .

Импульсная характеристика для напряжения конденсатора равна

${\displaystyle h_{C}(t)={\frac {1}{RC}}e^{-{\frac {t}{RC}}}u(t)={\frac {1}{\tau }}e^{-{\frac {t}{\tau }}}u(t)\,,}$

где u ( t ) — ступенчатая функция Хевисайда , а τ = RC — постоянная времени .

Аналогично импульсная характеристика для напряжения резистора равна

${\displaystyle h_{R}(t)=\delta (t)-{\frac {1}{RC}}e^{-{\frac {t}{RC}}}u(t)=\delta (t)-{\frac {1}{\tau }}e^{-{\frac {t}{\tau }}}u(t)\,,}$

где δ ( t ) — дельта-функция Дирака

Соображения в частотной области

Это выражения частотной области . Их анализ покажет, какие частоты схемы (или фильтры) пропускают, а какие отклоняют. Этот анализ основывается на рассмотрении того, что происходит с этими усилениями, когда частота становится очень большой и очень маленькой.

При ω → ∞ :

${\displaystyle G_{C}\to 0\quad {\mbox{and}}\quad G_{R}\to 1\,.}$

При ω → 0 :

${\displaystyle G_{C}\to 1\quad {\mbox{and}}\quad G_{R}\to 0\,.}$

Это показывает, что если выходной сигнал подается через конденсатор, высокие частоты ослабляются (замыкаются на землю), а низкие частоты пропускаются. Таким образом, схема ведет себя как фильтр нижних частот . Если же выходной сигнал подается через резистор, высокие частоты пропускаются, а низкие частоты ослабляются (поскольку конденсатор блокирует сигнал, когда его частота приближается к 0). В этой конфигурации схема ведет себя как фильтр верхних частот .

Диапазон частот, который пропускает фильтр, называется его полосой пропускания . Точка, в которой фильтр ослабляет сигнал до половины его нефильтрованной мощности, называется его частотой среза . Это требует, чтобы усиление схемы было уменьшено до

${\displaystyle G_{C}=G_{R}={\frac {1}{\sqrt {2}}}}$.

Решение приведенного выше уравнения дает

${\displaystyle \omega _{\mathrm {c} }={\frac {1}{RC}}\quad {\mbox{or}}\quad f_{\mathrm {c} }={\frac {1}{2\pi RC}}}$

это частота, которую фильтр ослабит до половины своей первоначальной мощности.

Очевидно, что фазы также зависят от частоты, хотя этот эффект в целом менее интересен, чем изменения усиления.

При ω → 0 :

${\displaystyle \phi _{C}\to 0\quad {\mbox{and}}\quad \phi _{R}\to 90^{\circ }={\frac {\pi }{2}}{\mbox{ radians}}\,.}$

При ω → ∞ :

${\displaystyle \phi _{C}\to -90^{\circ }=-{\frac {\pi }{2}}{\mbox{ radians}}\quad {\mbox{and}}\quad \phi _{R}\to 0\,.}$

Таким образом, при постоянном токе (0  Гц ) напряжение конденсатора совпадает по фазе с напряжением сигнала, в то время как напряжение резистора опережает его на 90°. По мере увеличения частоты напряжение конденсатора начинает отставать на 90° относительно сигнала, а напряжение резистора становится синфазным с сигналом.

Соображения временной области

В этом разделе используются знания e — натуральной логарифмической константы .

Самый простой способ вывести поведение во временной области — использовать преобразования Лапласа выражений для V _C и V _{R ,} приведенных выше. Это эффективно преобразует jω → s . Предполагая ступенчатый вход (т. е. V _in = 0 до t = 0 , а затем V _in = V после):

${\displaystyle {\begin{aligned}V_{\mathrm {in} }(s)&=V\cdot {\frac {1}{s}}\\V_{C}(s)&=V\cdot {\frac {1}{1+sRC}}\cdot {\frac {1}{s}}\\V_{R}(s)&=V\cdot {\frac {sRC}{1+sRC}}\cdot {\frac {1}{s}}\,.\end{aligned}}}$

Реакция конденсатора на скачок напряжения.

Реакция резистора на скачок напряжения.

Разложения простейших дробей и обратное преобразование Лапласа дают:

${\displaystyle {\begin{aligned}V_{C}(t)&=V\left(1-e^{-{\frac {t}{RC}}}\right)\\V_{R}(t)&=Ve^{-{\frac {t}{RC}}}\,.\end{aligned}}}$

Эти уравнения предназначены для расчета напряжения на конденсаторе и резисторе соответственно, пока конденсатор заряжается ; для разряда уравнения обратные. Эти уравнения можно переписать в терминах заряда и тока, используя соотношения C = ⁠В/В⁠ и V = IR (см.закон Ома).

Таким образом, напряжение на конденсаторе стремится к V с течением времени, в то время как напряжение на резисторе стремится к 0, как показано на рисунках. Это соответствует интуитивному представлению о том, что конденсатор будет заряжаться от напряжения питания с течением времени и в конечном итоге будет полностью заряжен.

Эти уравнения показывают, что последовательная RC-цепь имеет постоянную времени , обычно обозначаемую как τ = RC , которая представляет собой время, необходимое напряжению на компоненте для того, чтобы либо подняться (на конденсаторе), либо упасть (на резисторе) до значения, равного ⁠1/е⁠ его конечного значения. То есть, τ — это время, которое требуется V _C для достижения V (1 − ⁠1/е⁠ ) ​​и V _R для достижения V ( ⁠1/е⁠ ) ​​.

Скорость изменения дробная 1 − ⁠1/е⁠ за τ . Таким образом, при переходе от t = Nτ к t = ( N + 1) τ напряжение пройдет около 63,2% пути от своего уровня при t = Nτ к своему конечному значению. Таким образом, конденсатор будет заряжен примерно до 63,2% после τ и практически полностью заряжен (99,3%) примерно через 5 τ . Когда источник напряжения заменяется коротким замыканием, а конденсатор полностью заряжен, напряжение на конденсаторе экспоненциально падает с t от V до 0. Конденсатор будет разряжен примерно до 36,8% после τ и практически полностью разряжен (0,7%) примерно через 5 τ . Обратите внимание, что ток I в цепи ведет себя так же, как напряжение на резисторе, по закону Ома .

Эти результаты можно также получить путем решения дифференциальных уравнений, описывающих цепь:

${\displaystyle {\begin{aligned}{\frac {V_{\mathrm {in} }-V_{C}}{R}}&=C{\frac {dV_{C}}{dt}}\\V_{R}&=V_{\mathrm {in} }-V_{C}\,.\end{aligned}}}$

Первое уравнение решается с помощью интегрирующего множителя , а второе легко решается; решения точно такие же, как и полученные с помощью преобразований Лапласа.

Интегратор

Рассмотрим выходной сигнал на конденсаторе на высокой частоте, т.е.

${\displaystyle \omega \gg {\frac {1}{RC}}\,.}$

Это означает, что конденсатор не успевает зарядиться, и его напряжение очень мало. Таким образом, входное напряжение приблизительно равно напряжению на резисторе. Чтобы увидеть это, рассмотрим выражение для приведенного выше: ${\displaystyle I}$

${\displaystyle I={\frac {V_{\mathrm {in} }}{R+{\frac {1}{j\omega C}}}}\,,}$

но обратите внимание, что описанное частотное условие означает, что

${\displaystyle \omega C\gg {\frac {1}{R}}\,,}$

так

${\displaystyle I\approx {\frac {V_{\mathrm {in} }}{R}}}$

что является просто законом Ома .

Сейчас,

${\displaystyle V_{C}={\frac {1}{C}}\int _{0}^{t}I\,dt\,,}$

так

${\displaystyle V_{C}\approx {\frac {1}{RC}}\int _{0}^{t}V_{\mathrm {in} }\,dt\,,}$

который является интегратором на конденсаторе .

Дифференциатор

Рассмотрим выходной сигнал на резисторе на низкой частоте, т.е.

${\displaystyle \omega \ll {\frac {1}{RC}}\,.}$

Это означает, что конденсатор успевает зарядиться до тех пор, пока его напряжение не станет почти равным напряжению источника. Снова рассмотрим выражение для I , когда

${\displaystyle R\ll {\frac {1}{\omega C}}\,,}$

так

${\displaystyle {\begin{aligned}I&\approx {\frac {V_{\mathrm {in} }}{\frac {1}{j\omega C}}}\\V_{\mathrm {in} }&\approx {\frac {I}{j\omega C}}=V_{C}\,.\end{aligned}}}$

Сейчас,

${\displaystyle {\begin{aligned}V_{R}&=IR=C{\frac {dV_{C}}{dt}}R\\V_{R}&\approx RC{\frac {dV_{in}}{dt}}\,,\end{aligned}}}$

который является дифференциатором на резисторе .

Интеграция и дифференциация также могут быть достигнуты путем размещения резисторов и конденсаторов по мере необходимости на входе и в цепи обратной связи операционных усилителей (см. операционный усилитель-интегратор и операционный усилитель-дифференциатор ).

Последовательная RC-цепь ШИМ

Параллельная цепь

Параллельная RC-цепь

Параллельная RC-цепь, как правило, представляет меньший интерес, чем последовательная цепь. Это в значительной степени связано с тем, что выходное напряжение V _out равно входному напряжению V _in — в результате эта цепь не действует как фильтр на входном сигнале, если только она не питается от источника тока .

С комплексными сопротивлениями:

${\displaystyle {\begin{aligned}I_{R}&={\frac {V_{\mathrm {in} }}{R}}\\I_{C}&=j\omega CV_{\mathrm {in} }\,.\end{aligned}}}$

Это показывает, что ток конденсатора на 90° не совпадает по фазе с током резистора (и источника). В качестве альтернативы можно использовать следующие дифференциальные уравнения:

${\displaystyle {\begin{aligned}I_{R}&={\frac {V_{\mathrm {in} }}{R}}\\I_{C}&=C{\frac {dV_{\mathrm {in} }}{dt}}\,.\end{aligned}}}$

При питании от источника тока передаточная функция параллельной RC-цепи имеет вид:

${\displaystyle {\frac {V_{\mathrm {out} }}{I_{\mathrm {in} }}}={\frac {R}{1+sRC}}\,.}$

Синтез

Иногда требуется синтезировать RC-цепь из заданной рациональной функции в s . Для того чтобы синтез был возможен в пассивных элементах, функция должна быть положительно-действительной функцией . Для синтеза в виде RC-цепи все критические частоты ( полюса и нули ) должны находиться на отрицательной действительной оси и чередоваться между полюсами и нулями с равным количеством каждого. Кроме того, критическая частота, ближайшая к началу координат, должна быть полюсом, предполагая, что рациональная функция представляет собой импеданс, а не проводимость.

Синтез может быть достигнут с помощью модификации синтеза Фостера или синтеза Кауэра, используемых для синтеза LC-цепей . В случае синтеза Кауэра получится лестничная сеть резисторов и конденсаторов. ^[2]

Смотрите также

• Постоянная времени RC
• RL-цепь
• LC-контур
• RLC-цепь
• Электрическая сеть
• Список тем по электронике
• Реакция на шаг

Ссылки

1. Горовиц и Хилл, стр. 1.13
2. Бакши и Бакши, стр. 3-30–3-37

Библиография

• Бакши, У.А.; Бакши, А.В., Анализ цепей - II , Технические публикации, 2009 ISBN  9788184315974 .
• Горовиц, Пол; Хилл, Уинфилд, Искусство электроники (3-е издание), Cambridge University Press, 2015 ISBN 0521809266 .