Спиновое стекло

Неупорядоченное магнитное состояние

Схематическое изображение случайной спиновой структуры спинового стекла (вверху) и упорядоченной структуры ферромагнетика ( внизу)

Магнитный беспорядок спинового стекла по сравнению с ферромагнетиком аналогичен позиционному беспорядку стекла (слева) по сравнению с кварцем (справа).

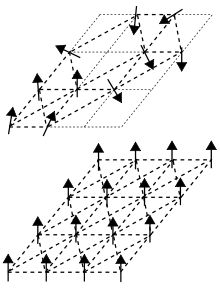
В физике конденсированного состояния спиновое стекло — это магнитное состояние, характеризующееся случайностью, помимо кооперативного поведения при замораживании спинов при температуре, называемой «температурой замораживания» T _f . ^[1] В ферромагнитных твердых телах все магнитные спины атомов-компонентов выстраиваются в одном направлении. Спиновое стекло в отличие от ферромагнетика определяется как « неупорядоченное » магнитное состояние, в котором спины выстраиваются случайным образом или без регулярного рисунка, а связи также случайны. ^[1]

Термин «стекло» происходит от аналогии между магнитным беспорядком в спиновом стекле и позиционным беспорядком обычного химического стекла , например, оконного стекла. В оконном стекле или любом аморфном твердом теле структура атомных связей крайне нерегулярна; в противоположность этому кристалл имеет однородную структуру атомных связей. В ферромагнитных твердых телах все магнитные спины выстраиваются в одном направлении; это аналогично решеточной структуре кристалла .

Отдельные атомные связи в спиновом стекле представляют собой смесь примерно равного количества ферромагнитных связей (где соседи имеют одинаковую ориентацию) и антиферромагнитных связей (где соседи имеют совершенно противоположную ориентацию: северный и южный полюса перевернуты на 180 градусов). Эти модели выровненных и невыровненных атомных магнитов создают то, что известно как фрустрированные взаимодействия  — искажения в геометрии атомных связей по сравнению с тем, что можно было бы увидеть в обычном, полностью выровненном твердом теле. Они также могут создавать ситуации, когда более чем одно геометрическое расположение атомов является стабильным.

Существует два основных аспекта спинового стекла. С физической стороны спиновые стекла представляют собой реальные материалы с отличительными свойствами, обзор которых. ^[2] С математической стороны, простые статистические механические модели, вдохновленные реальными спиновыми стеклами, широко изучаются и применяются. ^[3]

Спиновые стекла и сложные внутренние структуры, которые возникают в них, называются « метастабильными », потому что они «застревают» в стабильных конфигурациях, отличных от конфигурации с самой низкой энергией (которая была бы выровненной и ферромагнитной). Математическая сложность этих структур трудна, но плодотворна для экспериментального изучения или моделирования ; с приложениями к физике, химии, материаловедению и искусственным нейронным сетям в информатике .

Магнитное поведение

Именно зависимость от времени отличает спиновые стекла от других магнитных систем.

Выше температуры перехода в спиновое стекло , T _c , ^{[примечание 1]} спиновое стекло проявляет типичное магнитное поведение (такое как парамагнетизм ).

Если при охлаждении образца до температуры перехода применяется магнитное поле , намагниченность образца увеличивается, как описано законом Кюри . При достижении T _c образец становится спиновым стеклом, и дальнейшее охлаждение приводит к небольшому изменению намагниченности. Это называется намагничиванием , охлажденным полем .

При удалении внешнего магнитного поля намагниченность спинового стекла быстро падает до более низкого значения, известного как остаточная намагниченность.

Намагниченность затем медленно затухает по мере приближения к нулю (или некоторой малой доле от исходного значения – это остается неизвестным ). Этот затухание не является экспоненциальным , и никакая простая функция не может адекватно описать кривую намагниченности во времени. ^[4] Этот медленный затухание характерен для спиновых стекол. Экспериментальные измерения порядка дней показали непрерывные изменения выше уровня шума приборов. ^[4]

Спиновые стекла отличаются от ферромагнитных материалов тем, что после снятия внешнего магнитного поля с ферромагнитного вещества намагниченность остается на неопределенно долгом уровне остаточного значения. Парамагнитные материалы отличаются от спиновых стекол тем, что после снятия внешнего магнитного поля намагниченность быстро падает до нуля, при этом остаточная намагниченность отсутствует. Спад быстрый и экспоненциальный. ^{[ необходима цитата ]}

Если образец охлаждается ниже T _c в отсутствие внешнего магнитного поля, а магнитное поле прикладывается после перехода в фазу спинового стекла, происходит быстрое начальное увеличение до значения, называемого намагниченностью, охлажденной в нулевом поле . Затем происходит медленный дрейф вверх в сторону намагниченности, охлажденной в поле.

Удивительно, но сумма двух сложных функций времени (охлажденной в нулевом поле и остаточной намагниченности) является константой, а именно значением, охлажденным в поле, и, таким образом, обе имеют идентичные функциональные формы со временем ^[5] , по крайней мере, в пределе очень малых внешних полей.

Модель Эдвардса–Андерсона

Это похоже на модель Изинга . В этой модели у нас есть спины, расположенные на -мерной решетке с взаимодействиями только ближайших соседей . Эта модель может быть решена точно для критических температур, и стеклообразная фаза наблюдается при низких температурах. ^[6] Гамильтониан для этой спиновой системы определяется как: ${\displaystyle d}$

${\displaystyle H=-\sum _{\langle ij\rangle }J_{ij}S_{i}S_{j},}$

где относится к матрице спина Паули для спин-получастицы в точке решетки , а сумма по относится к суммированию по соседним точкам решетки и . Отрицательное значение обозначает взаимодействие антиферромагнитного типа между спинами в точках и . Сумма пробегает все ближайшие соседние позиции на решетке любой размерности. Переменные, представляющие магнитную природу спин-спиновых взаимодействий, называются переменными связи или зацепления. ${\displaystyle S_{i}}$ ${\displaystyle i}$ ${\displaystyle \langle ij\rangle }$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle J_{ij}}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle J_{ij}}$

Чтобы определить функцию распределения для этой системы, необходимо усреднить свободную энергию , где , по всем возможным значениям . Распределение значений принимается гауссовым со средним значением и дисперсией : ${\displaystyle f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]}$ ${\displaystyle {\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)}$ ${\displaystyle J_{ij}}$ ${\displaystyle J_{ij}}$ ${\displaystyle J_{0}}$ ${\displaystyle J^{2}}$

${\displaystyle P(J_{ij})={\sqrt {\frac {N}{2\pi J^{2}}}}\exp \left\{-{\frac {N}{2J^{2}}}\left(J_{ij}-{\frac {J_{0}}{N}}\right)^{2}\right\}.}$

При решении задачи определения свободной энергии с использованием метода реплик ниже определенной температуры обнаруживается существование новой магнитной фазы, называемой фазой спинового стекла (или стекловидной фазой) системы, которая характеризуется исчезающей намагниченностью вместе с неисчезающим значением двухточечной корреляционной функции между спинами в одной и той же точке решетки, но в двух разных репликах: ${\displaystyle m=0}$

${\displaystyle q=\sum _{i=1}^{N}S_{i}^{\alpha }S_{i}^{\beta }\neq 0,}$

где — индексы реплик. Параметр порядка для фазового перехода из ферромагнетика в спиновое стекло равен , а для парамагнетика в спиновое стекло снова равен . Следовательно, новый набор параметров порядка, описывающих три магнитные фазы, состоит из и . ${\displaystyle \alpha ,\beta }$ ${\displaystyle q}$ ${\displaystyle q}$ ${\displaystyle m}$ ${\displaystyle q}$

В предположении симметрии реплики средняя свободная энергия поля определяется выражением: ^[6]

${\displaystyle {\begin{aligned}\beta f={}-{\frac {\beta ^{2}J^{2}}{4}}(1-q)^{2}+{\frac {\beta J_{0}m^{2}}{2}}-\int \exp \left(-{\frac {z^{2}}{2}}\right)\log \left(2\cosh \left(\beta Jz+\beta J_{0}m\right)\right)\,\mathrm {d} z.\end{aligned}}}$

Модель Шеррингтона–Киркпатрика

В дополнение к необычным экспериментальным свойствам, спиновые стекла являются предметом обширных теоретических и вычислительных исследований. Значительная часть ранних теоретических работ по спиновым стеклам касалась формы теории среднего поля, основанной на наборе реплик функции распределения системы.

Важная, точно решаемая модель спинового стекла была введена Дэвидом Шеррингтоном и Скоттом Киркпатриком в 1975 году. Это модель Изинга с дальнодействующими фрустрированными ферро- и антиферромагнитными связями. Она соответствует приближению среднего поля спиновых стекол, описывающему медленную динамику намагниченности и сложное неэргодическое равновесное состояние.

В отличие от модели Эдвардса–Андерсона (EA), в системе, хотя рассматриваются только двухспиновые взаимодействия, диапазон каждого взаимодействия может быть потенциально бесконечным (порядка размера решетки). Поэтому мы видим, что любые два спина могут быть связаны ферромагнитной или антиферромагнитной связью, и распределение их задается точно так же, как в случае модели Эдвардса–Андерсона. Гамильтониан для модели SK очень похож на модель EA:

${\displaystyle H=-{\frac {1}{\sqrt {N}}}\sum _{i<j}J_{ij}S_{i}S_{j}}$

где имеют те же значения, что и в модели EA. Равновесное решение модели, после некоторых первоначальных попыток Шеррингтона, Киркпатрика и других, было найдено Джорджио Паризи в 1979 году с помощью метода реплик. Последующая работа по интерпретации решения Паризи — М. Мезардом , Дж. Паризи , М. А. Вирасоро и многими другими — выявила сложную природу стеклообразной низкотемпературной фазы, характеризующейся нарушением эргодичности, ультраметричностью и несамоусредняемостью. Дальнейшие разработки привели к созданию метода полости , который позволил изучать низкотемпературную фазу без реплик. Строгое доказательство решения Паризи было предоставлено в работе Франческо Гуэрры и Мишеля Талагранда . ^[7] ${\displaystyle J_{ij},S_{i},S_{j}}$

Фазовая диаграмма

Кривая де Алмейды-Таулесса.

При наличии однородного внешнего магнитного поля величиной , энергетическая функция становится Пусть все связи являются выборками IID из гауссовского распределения среднего 0 и дисперсии . В 1979 году Дж. Р. Л. де Алмейда и Дэвид Таулесс ^[8] обнаружили, что, как и в случае модели Изинга, решение среднего поля для модели SK становится нестабильным в состоянии низкой температуры и низкого магнитного поля. ${\displaystyle M}$ $${\displaystyle H=-{\frac {1}{\sqrt {N}}}\sum _{i<j}J_{ij}S_{i}S_{j}-M\sum _{i}S_{i}}$$ ${\displaystyle J_{ij}}$ ${\displaystyle J^{2}}$

Область устойчивости на фазовой диаграмме модели SK определяется двумя безразмерными параметрами . Ее фазовая диаграмма состоит из двух частей, разделенных кривой де Алмейды-Таулесса , Кривая является решением уравнений ^[8] Фазовый переход происходит при . Чуть ниже нее мы имеем При низкой температуре, высоком пределе магнитного поля линия ${\displaystyle x:={\frac {kT}{J}},\quad y:={\frac {M}{J}}}$ $${\displaystyle {\begin{aligned}&x^{2}={\frac {1}{(2\pi )^{1/2}}}\int \mathrm {d} z\;\mathrm {e} ^{-{\frac {1}{2}}z^{2}}\operatorname {sech} ^{4}\left({\frac {q^{1/2}z+y}{x}}\right),\\&q={\frac {1}{(2\pi )^{1/2}}}\int \mathrm {d} z\;\mathrm {e} ^{-{\frac {1}{2}}z^{2}}\tanh ^{2}\left({\frac {q^{1/2}z+y}{x}}\right).\end{aligned}}}$$ ${\displaystyle x=1}$ $${\displaystyle y^{2}\approx {\frac {4}{3}}(1-x)^{3}.}$$ $${\displaystyle x\approx {\frac {4}{3{\sqrt {2\pi }}}}e^{-{\frac {1}{2}}y^{2}}}$$

Модель с бесконечным диапазоном

Это также называется "моделью p-спин". ^[3] Модель бесконечного диапазона является обобщением модели Шеррингтона–Киркпатрика, в которой мы рассматриваем не только двухспиновые взаимодействия, но и -спиновые взаимодействия, где и - общее число спинов. В отличие от модели Эдвардса–Андерсона, но подобно модели SK, диапазон взаимодействия бесконечен. Гамильтониан для этой модели описывается следующим образом: ${\displaystyle p}$ ${\displaystyle p\leq N}$ ${\displaystyle N}$

${\displaystyle H=-\sum _{i_{1}<i_{2}<\cdots <i_{p}}J_{i_{1}\dots i_{p}}S_{i_{1}}\cdots S_{i_{p}}}$

где имеют схожие значения, как в модели EA. Предел этой модели известен как модель случайной энергии . В этом пределе вероятность существования спинового стекла в определенном состоянии зависит только от энергии этого состояния, а не от индивидуальных конфигураций спинов в нем. Обычно предполагается, что для решения этой модели используется гауссовское распределение магнитных связей по решетке. Ожидается, что любое другое распределение даст тот же результат, как следствие центральной предельной теоремы . Гауссова функция распределения со средним значением и дисперсией задается как: ${\displaystyle J_{i_{1}\dots i_{p}},S_{i_{1}},\dots ,S_{i_{p}}}$ ${\displaystyle p\to \infty }$ ${\displaystyle {\frac {J_{0}}{N}}}$ ${\displaystyle {\frac {J^{2}}{N}}}$

${\displaystyle P\left(J_{i_{1}\cdots i_{p}}\right)={\sqrt {\frac {N^{p-1}}{J^{2}\pi p!}}}\exp \left\{-{\frac {N^{p-1}}{J^{2}p!}}\left(J_{i_{1}\cdots i_{p}}-{\frac {J_{0}p!}{2N^{p-1}}}\right)\right\}}$

Параметры порядка для этой системы задаются намагниченностью и двухточечной спиновой корреляцией между спинами в одном и том же месте в двух различных репликах, которые совпадают с моделью SK. Эта модель бесконечного диапазона может быть решена явно для свободной энергии ^[6] в терминах и , при предположении симметрии реплики, а также нарушения симметрии 1-реплики. ^[6] ${\displaystyle m}$ ${\displaystyle q}$ ${\displaystyle m}$ ${\displaystyle q}$

${\displaystyle {\begin{aligned}\beta f={}&{\frac {1}{4}}\beta ^{2}J^{2}q^{p}-{\frac {1}{2}}p\beta ^{2}J^{2}q^{p}-{\frac {1}{4}}\beta ^{2}J^{2}+{\frac {1}{2}}\beta J_{0}pm^{p}+{\frac {1}{4{\sqrt {2\pi }}}}p\beta ^{2}J^{2}q^{p-1}+{}\\&\int \exp \left(-{\frac {1}{2}}z^{2}\right)\log \left(2\cosh \left(\beta Jz{\sqrt {{\frac {1}{2}}pq^{p-1}}}+{\frac {1}{2}}\beta J_{0}pm^{p-1}\right)\right)\,\mathrm {d} z\end{aligned}}}$

Неэргодическое поведение и приложения

Термодинамическая система является эргодической , когда при любом (равновесном) экземпляре системы она в конечном итоге посещает все другие возможные (равновесные) состояния (той же энергии). Одной из характеристик систем спинового стекла является то, что ниже температуры замерзания экземпляры оказываются в «неэргодическом» наборе состояний: система может колебаться между несколькими состояниями, но не может перейти в другие состояния с эквивалентной энергией. Интуитивно можно сказать, что система не может вырваться из глубоких минимумов иерархически неупорядоченного энергетического ландшафта ; расстояния между минимумами задаются ультраметрикой с высокими энергетическими барьерами между минимумами. ^{[примечание 2]} Коэффициент участия подсчитывает количество состояний, которые доступны из данного экземпляра, то есть количество состояний, которые участвуют в основном состоянии . Эргодический аспект спинового стекла сыграл важную роль в присуждении половины Нобелевской премии по физике 2021 года Джорджио Паризи . ^{[9] [10] [11]} ${\displaystyle T_{\text{f}}}$

Для физических систем, таких как разбавленный марганец в меди, температура замерзания обычно составляет всего 30 кельвинов (−240 °C), и поэтому магнетизм спинового стекла, по-видимому, практически не имеет приложений в повседневной жизни. Неэргодические состояния и грубые энергетические ландшафты, однако, весьма полезны для понимания поведения определенных нейронных сетей , включая сети Хопфилда , а также многих проблем оптимизации компьютерных наук и генетики .

Спиновое стекло без структурного беспорядка

Элементарный кристаллический неодим является парамагнитным при комнатной температуре и становится антиферромагнетиком с несоразмерным порядком при охлаждении ниже 19,9 К. ^[12] Ниже этой температуры перехода он демонстрирует сложный набор магнитных фаз ^{[13] [14]} , которые имеют длительное время релаксации спина и поведение спинового стекла, которое не зависит от структурного беспорядка. ^[15]

История

Подробный отчет об истории спиновых стекол с начала 1960-х до конца 1980-х годов можно найти в серии популярных статей Филипа У. Андерсона в журнале Physics Today . ^{[16] [17] [18] [19] [20] [21] [22] [23]}

Открытие

В 1930-х годах материаловеды открыли эффект Кондо , при котором удельное сопротивление номинально чистого золота достигает минимума при 10 К, а для номинально чистой меди — при 2 К. Позднее стало понятно, что эффект Кондо возникает, когда немагнитный металл насыщается разбавленными магнитными атомами.

Необычное поведение наблюдалось в сплаве железа в золоте (Au Fe ) и сплаве марганца в меди (Cu Mn ) при концентрации около 1–10 атомных процентов . Каннелла и Мидош в 1972 году ^[24] обнаружили , что Au Fe имел неожиданный пик в виде острого выступа в восприимчивости переменного тока при четко определенной температуре, которая позже была названа температурой замерзания спинового стекла . ^[25]

Его также называли «миктомагнетиком» (micto- по-гречески означает «смешанный»). Термин возник из наблюдения, что эти материалы часто содержат смесь ферромагнитных ( ) и антиферромагнитных ( ) взаимодействий, что приводит к их неупорядоченной магнитной структуре. Этот термин вышел из употребления по мере развития теоретического понимания спиновых стекол, признающего, что магнитная фрустрация возникает не только из простой смеси ферро- и антиферромагнитных взаимодействий, но и из-за их случайности и фрустрации в системе. ${\displaystyle J>0}$ ${\displaystyle J<0}$

Модель Шеррингтона-Киркпатрика

Шеррингтон и Киркпатрик предложили модель SK в 1975 году и решили ее методом реплик. ^[26] Они обнаружили, что при низких температурах ее энтропия становится отрицательной, что, по их мнению, объясняется тем, что метод реплик является эвристическим методом, который неприменим при низких температурах.

Затем было обнаружено, что метод реплик был правильным, но проблема заключается в том, что низкотемпературная нарушенная симметрия в модели SK не может быть охарактеризована исключительно параметром порядка Эдвардса-Андерсона. Вместо этого необходимы дополнительные параметры порядка, что приводит к анзацу Джорджио Паризи, разрушающему реплики . При полном анзаце, разрушающем реплики, требуется бесконечно много параметров порядка, чтобы охарактеризовать стабильное решение. ^[27]

Приложения

Формализм теории среднего поля реплик также применялся при изучении нейронных сетей , где он позволил рассчитать такие свойства, как емкость памяти простых архитектур нейронных сетей, не требуя разработки или реализации алгоритма обучения (например, обратного распространения ). ^[28]

Более реалистичные модели спинового стекла с короткодействующими фрустрированными взаимодействиями и беспорядком, такие как гауссовская модель, где связи между соседними спинами следуют гауссовскому распределению , также были широко изучены, особенно с использованием моделирования Монте-Карло . Эти модели отображают фазы спинового стекла, ограниченные резкими фазовыми переходами .

Помимо своей значимости в физике конденсированного состояния, теория спинового стекла приобрела ярко выраженный междисциплинарный характер и находит применение в теории нейронных сетей , информатике, теоретической биологии, эконофизике и т. д.

Модели спинового стекла были адаптированы к модели сворачивания белка по принципу воронкообразной структуры .

Смотрите также

• Аморфный магнит
• Антиферромагнитное взаимодействие
• Метод полости
• Кристаллическая структура
• Геометрическая фрустрация
• Ориентационный стакан
• Фазовый переход
• Потушенный беспорядок
• Модель случайной энергии
• Трюк с репликой
• Физика твердого тела
• Спин-лёд

Примечания

1. идентична так называемой «температуре замерзания» ${\displaystyle T_{\text{c}}}$ ${\displaystyle T_{\text{f}}.}$
2. Иерархический беспорядок энергетического ландшафта можно вербально охарактеризовать одним предложением: в этом ландшафте есть «(случайные) долины внутри еще более глубоких (случайных) долин внутри еще более глубоких (случайных) долин, ... и т. д.»

Ссылки

1. Mydosh, JA (1993). Spin Glasses: An Experimental Introduction . Лондон, Вашингтон, округ Колумбия: Taylor & Francis. стр. 3. ISBN 0748400389. 9780748400386 .
2. Форд, Питер Дж. (март 1982 г.). «Спиновые стекла». Contemporary Physics . 23 (2): 141–168. Bibcode : 1982ConPh..23..141F. doi : 10.1080/00107518208237073. ISSN  0010-7514.
3. Mézard, Marc; Montanari, Andrea (2009). Информация, физика и вычисления . Тексты для выпускников Оксфорда. Оксфорд: Oxford university press. ISBN 978-0-19-857083-7.
4. Joy, PA; Kumar, PS Anil; Date, SK (7 октября 1998 г.). "Соотношение между охлажденными в поле и охлажденными в нулевом поле восприимчивостями некоторых упорядоченных магнитных систем". J. Phys.: Condens. Matter . 10 (48): 11049–11054. Bibcode :1998JPCM...1011049J. doi :10.1088/0953-8984/10/48/024. S2CID  250734239.
5. Nordblad, P.; Lundgren, L.; Sandlund, L. (февраль 1986). "Связь между релаксацией нулевого поля при охлаждении и термоостаточной намагниченностью в спиновых стеклах". Журнал магнетизма и магнитных материалов . 54–57 (1): 185–186. Bibcode : 1986JMMM...54..185N. doi : 10.1016/0304-8853(86)90543-3.
6. Нисимори, Хидетоши (2001). Статистическая физика спиновых стекол и обработка информации: Введение . Оксфорд: Oxford University Press. стр. 243. ISBN 9780198509400.
7. Мишель Талагран, Модели среднего поля для спиновых стекол. Том I: Основные примеры (2010)
8. Almeida, JRL de; Thouless, DJ (май 1978). "Устойчивость решения Шеррингтона-Киркпатрика модели спинового стекла". Journal of Physics A: Mathematical and General . 11 (5): 983–990. Bibcode :1978JPhA...11..983D. doi :10.1088/0305-4470/11/5/028. ISSN  0305-4470.
9. Геддес, Линда (2021-10-05). «Трио ученых получили Нобелевскую премию по физике за работу по климату». The Guardian . Получено 2023-12-23 .
10. "Нобелевская премия по физике 2021 года - Популярная научная подоплека" (PDF) . Получено 23.12.2023 .
11. "Научное обоснование Нобелевской премии по физике 2021 года" (PDF) . Нобелевский комитет по физике . 5 октября 2021 г. . Получено 3 ноября 2023 г. .
12. Андрей Шитула; Януш Лецеевич (8 марта 1994 г.). Справочник по кристаллическим структурам и магнитным свойствам редкоземельных интерметаллидов. CRC Press. стр. 1. ISBN 978-0-8493-4261-5.
13. Зоховски, SW; Макьюэн, KA; Фосетт, E (1991). «Магнитные фазовые диаграммы неодима». Журнал физики: конденсированное вещество . 3 (41): 8079–8094. Bibcode : 1991JPCM....3.8079Z. doi : 10.1088/0953-8984/3/41/007. ISSN  0953-8984.
14. Lebech, B; Wolny, J; Moon, RM (1994). «Магнитные фазовые переходы в двойном гексагональном плотноупакованном металле неодима, соизмеримом в двух измерениях». Journal of Physics: Condensed Matter . 6 (27): 5201–5222. Bibcode : 1994JPCM....6.5201L. doi : 10.1088/0953-8984/6/27/029. ISSN  0953-8984.
15. Камбер, Умут; Бергман, Андерс; Эйх, Андреас; Юшан, Диана; Штайнбрехер, Мануэль; Гауптманн, Надин; Нордстрем, Ларс; Кацнельсон Михаил Игоревич; Вегнер, Дэниел; Эрикссон, Олле; Хаджетурян, Александр А. (2020). «Самоиндуцированное состояние спинового стекла в элементарном и кристаллическом неодиме». Наука . 368 (6494). arXiv : 1907.02295 . doi : 10.1126/science.aay6757. ISSN  0036-8075. ПМИД  32467362.
16. Филип В. Андерсон (1988). «Спиновое стекло I: спасенный закон масштабирования» (PDF) . Physics Today . 41 (1): 9–11. Bibcode : 1988PhT....41a...9A. doi : 10.1063/1.2811268.
17. Филип В. Андерсон (1988). «Спиновое стекло II: существует ли фазовый переход?» (PDF) . Physics Today . 41 (3): 9. Bibcode : 1988PhT....41c...9A. doi : 10.1063/1.2811336.
18. Филип В. Андерсон (1988). «Спиновое стекло III: теория поднимает голову» (PDF) . Physics Today . 41 (6): 9–11. Bibcode : 1988PhT....41f...9A. doi : 10.1063/1.2811440.
19. Филип В. Андерсон (1988). «Спиновое стекло IV: Проблески неприятностей» (PDF) . Physics Today . 41 (9): 9–11. Bibcode : 1988PhT....41i...9A. doi : 10.1063/1.881135.
20. Филип В. Андерсон (1989). «Спиновое стекло V: Реальная сила, привнесенная в медвежью игру» (PDF) . Physics Today . 42 (7): 9–11. Bibcode : 1989PhT....42g...9A. doi : 10.1063/1.2811073.
21. Филип В. Андерсон (1989). «Спиновое стекло VI: Спиновое стекло как рог изобилия» (PDF) . Physics Today . 42 (9): 9–11. Bibcode : 1989PhT....42i...9A. doi : 10.1063/1.2811137.
22. Филип В. Андерсон (1990). «Спиновое стекло VII: спиновое стекло как парадигма» (PDF) . Physics Today . 43 (3): 9–11. Bibcode : 1990PhT....43c...9A. doi : 10.1063/1.2810479.
23. Все они вместе взятые.
24. Каннелла, В.; Мидош, JA (1 декабря 1972 г.). «Магнитное упорядочение в сплавах золота и железа». Physical Review B. 6 ( 11): 4220–4237. Bibcode : 1972PhRvB...6.4220C. doi : 10.1103/PhysRevB.6.4220.
25. Mulder, CAM; van Duyneveldt, AJ; Mydosh, JA (1981-02-01). "Восприимчивость спинового стекла $\mathrm{Cu}\mathrm{Mn}$: частотные и полевые зависимости". Physical Review B. 23 ( 3): 1384–1396. doi :10.1103/PhysRevB.23.1384.
26. Шеррингтон, Дэвид; Киркпатрик, Скотт (1975-12-29). «Решаемая модель спинового стекла». Physical Review Letters . 35 (26): 1792–1796. Bibcode : 1975PhRvL..35.1792S. doi : 10.1103/physrevlett.35.1792. ISSN  0031-9007.
27. Паризи, Г. (1979-12-03). «Бесконечное число параметров порядка для спиновых стекол». Physical Review Letters . 43 (23): 1754–1756. Bibcode : 1979PhRvL..43.1754P. doi : 10.1103/PhysRevLett.43.1754. ISSN  0031-9007.
28. Гарднер, Э.; Деридда, Б. (7 января 1988 г.). "Оптимальные свойства хранения моделей нейронных сетей" (PDF) . J. Phys. A. 21 ( 1): 271. Bibcode : 1988JPhA...21..271G. doi : 10.1088/0305-4470/21/1/031.

Литература

Экспозиции

• Stein, Daniel L.; Newman, Charles M. (2013). Спиновые стекла и сложность . Праймеры в сложных системах. Princeton: Princeton University Press. ISBN 978-0-691-14733-8.Популярное изложение, с минимальным количеством математики.
• Монтанари, Андреа; Сен, Субхабрата (2024-01-09). «Дружественный учебник по методам спинового стекла среднего поля для нефизиков». Основы и тенденции в машинном обучении . 17 (1): 1–173. arXiv : 2204.02909 . doi : 10.1561/2200000105. ISSN  1935-8237.Введение в практическое руководство.
• Mézard, Marc; Montanari, Andrea (2009). Информация, физика и вычисления. Оксфорд, Великобритания: Oxford University Press. ISBN 9780198570837. OCLC  234430714.Первые 15 глав черновой версии 2008 года, доступные на сайте www.stat.ucla.edu. Учебник, в котором основное внимание уделяется методу полостных уравнений и его применению в информатике, особенно проблемам удовлетворения ограничений .
• Нисимори, Хидетоши (2001). Статистическая физика спиновых стекол и обработка информации: введение. Международная серия монографий по физике. Оксфорд; Нью-Йорк: Oxford University Press. ISBN 978-0-19-850940-0. OCLC  47063323.Введение сосредоточено на приложениях компьютерной науки, включая нейронные сети.
• Mydosh, JA (1993). Спиновые стекла: экспериментальное введение . Лондон; Вашингтон, округ Колумбия: Тейлор и Фрэнсис. ISBN 978-0-7484-0038-6.Основное внимание уделяется экспериментально измеряемым свойствам спиновых стекол (например, сплава меди и марганца).
• Фишер, К. Х.; Герц, Джон (1991). Спиновые стекла . Кембриджские исследования магнетизма. Кембридж; Нью-Йорк, США: Cambridge University Press. ISBN 978-0-521-34296-4.Охватывает теорию среднего поля , экспериментальные данные и численное моделирование.
• Мезард, Марк; Паризи, Джорджио ; Вирасоро, Мигель Анхель (1987), Теория спинового стекла и не только , Сингапур: World Scientific, ISBN 978-9971-5-0115-0. Раннее изложение, содержащее прорывы, предшествовавшие 1990-м годам, такие как трюк с копией .
• De Dominicis, Cirano; Giardina, Irene (2006). Случайные поля и спиновые стекла: подход теории поля. Кембридж, Великобритания; Нью-Йорк: Cambridge University Press. ISBN 978-0-521-84783-4. OCLC  70764844.Подход с использованием статистической теории поля .
• Талагранд, Мишель (2010). Модели среднего поля для спиновых стекол. 1: Основные примеры . Ergebnisse der Mathematik und ihrer Grenzgebiete (Редакция в мягкой обложке 1-го издания, 2010 г.). Берлин Гейдельберг: Springer. ISBN 978-3-642-26598-3.и Талагранд, Мишель (2011). Модели среднего поля для спиновых стекол. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Фольге = Серия современных обзоров по математике. Гейдельберг; Нью-Йорк: Спрингер. ISBN 978-3-642-15201-6. OCLC  733249730.. Сборник строго доказуемых результатов.

Первичные источники

• Эдвардс, С. Ф.; Андерсон, П. В. (1975), «Теория спиновых стекол», Журнал физики F: Физика металлов , 5 (5): 965–974, Bibcode : 1975JPhF....5..965E, doi : 10.1088/0305-4608/5/5/017. ShieldSquare Captcha
• Шеррингтон, Дэвид; Киркпатрик, Скотт (1975), «Решаемая модель спинового стекла», Physical Review Letters , 35 (26): 1792–1796, Bibcode : 1975PhRvL..35.1792S, doi : 10.1103/PhysRevLett.35.1792. Резюме Papercore http://papercore.org/Sherrington1975
• Нордблад, П.; Лундгрен, Л.; Сандлунд, Л. (1986), «Связь между релаксацией нулевого поля при охлаждении и термоостаточной намагниченностью в спиновых стеклах», Журнал магнетизма и магнитных материалов , 54 : 185–186, Bibcode : 1986JMMM...54..185N, doi : 10.1016/0304-8853(86)90543-3.
• Биндер, К.; Янг, А.П. (1986), «Спиновые стекла: экспериментальные факты, теоретические концепции и открытые вопросы», Reviews of Modern Physics , 58 (4): 801–976, Bibcode : 1986RvMP...58..801B, doi : 10.1103/RevModPhys.58.801.
• Брингельсон, Джозеф Д.; Волинес, Питер Г. (1987), «Спиновые стекла и статистическая механика сворачивания белков», Труды Национальной академии наук , 84 (21): 7524–7528, Bibcode : 1987PNAS...84.7524B, doi : 10.1073/pnas.84.21.7524 , PMC  299331 , PMID  3478708....
• Паризи, Г. (1980), «Параметр порядка для спиновых стекол: функция на интервале 0-1» (PDF) , J. Phys. A: Math. Gen. , 13 (3): 1101–1112, Bibcode : 1980JPhA...13.1101P, doi : 10.1088/0305-4470/13/3/042Резюме Papercore http://papercore.org/Parisi1980.
• Талагранд, Мишель (2000), «Нарушение симметрии реплики и экспоненциальные неравенства для модели Шеррингтона–Киркпатрика», Annals of Probability , 28 (3): 1018–1062, doi : 10.1214/aop/1019160325 , JSTOR  2652978.
• Guerra, F.; Toninelli, FL (2002), "Термодинамический предел в моделях спинового стекла среднего поля", Communications in Mathematical Physics , 230 (1): 71–79, arXiv : cond-mat/0204280 , Bibcode : 2002CMaPh.230...71G, doi : 10.1007/s00220-002-0699-y, S2CID  16833848

Внешние ссылки

• Статистика частоты термина «Спиновое стекло» в arxiv.org