В истории физики прорывом стала работа « О квантово-теоретической реинтерпретации кинематических и механических связей » ( нем . Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen ), также известная как статья Umdeutung ( переинтерпретация ) , [1] [2]. статья по квантовой механике, написанная Вернером Гейзенбергом , которая появилась в Zeitschrift für Physik в сентябре 1925 года.
В статье Гейзенберг попытался объяснить энергетические уровни одномерного ангармонического осциллятора , избегая конкретных, но ненаблюдаемых представлений электронных орбит , используя наблюдаемые параметры, такие как вероятности переходов для квантовых скачков , что потребовало использования двух индексов, соответствующих начальному и конечному состояниям. [3]
Математически Гейзенберг показал необходимость некоммутативных операторов. Это понимание позже стало основой принципа неопределенности Гейзенберга .
За этой статьей последовала статья Паскуаля Йордана и Макса Борна того же года [4] и «статья трех человек» ( нем . drei Männer Arbeit ) Борна, Гейзенберга и Йордана в 1926 году. [5] [1] [6] Эти статьи заложили основу для матричной механики , которая пришла на смену старой квантовой теории , приведя к современной квантовой механике. Гейзенберг получил Нобелевскую премию по физике в 1932 году за свою работу по развитию квантовой механики. [7]
Гейзенбергу было 23 года, когда он работал над статьей, выздоравливая от сенной лихорадки на острове Гельголанд , переписываясь с Вольфгангом Паули по этому поводу. Когда его спросили о его мнении о рукописи, Паули ответил положительно, но Гейзенберг сказал, что он все еще «очень не уверен в ней». В июле 1925 года он отправил рукопись Максу Борну для рецензирования и решения о том, следует ли представлять ее для публикации. [8]
Когда Борн прочитал статью, он узнал формулировку как ту, которую можно было бы транскрибировать и расширить до систематического языка матриц. Борн, с помощью своего помощника и бывшего студента Паскуаля Джордана, немедленно начал делать транскрипцию и расширение, и они представили свои результаты для публикации; их рукопись была получена для публикации всего через 60 дней после статьи Гейзенберга. [4] Последующая статья всех трех авторов, расширяющая теорию до нескольких измерений, была представлена для публикации до конца года. [5]
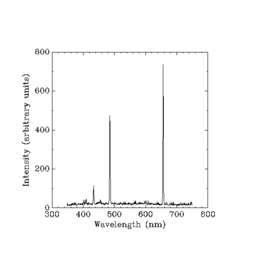
Гейзенберг решил основывать свою квантовую механику «исключительно на соотношениях между величинами, которые в принципе можно наблюдать». [9] Он заметил, что тогда нельзя использовать какие-либо утверждения о таких вещах, как «положение и период обращения электрона». [10] Скорее, чтобы добиться настоящего прогресса в понимании излучения простейшего случая, излучения возбужденных атомов водорода, нужно было работать только с измерениями частот и интенсивностей ярко-линейчатого спектра водорода.

В классической физике интенсивность каждой частоты света, произведенного в излучающей системе, равна квадрату амплитуды излучения на этой частоте, поэтому внимание затем упало на амплитуды. Классические уравнения, которые Гейзенберг надеялся использовать для формирования квантово-теоретических уравнений, сначала давали бы амплитуды, а в классической физике можно было бы вычислить интенсивности просто путем возведения амплитуд в квадрат. Но Гейзенберг видел, что «самым простым и естественным предположением было бы» [11] следовать примеру, предоставленному недавней работой по вычислению дисперсии света, выполненной Гансом Крамерсом [12] . Работа, которую он проделал, помогая Крамерсу в предыдущем году [13], теперь дала ему важную подсказку о том, как моделировать то, что происходило с возбужденным водородным газом, когда он излучал свет, и что происходило, когда входящее излучение одной частоты возбуждало атомы в дисперсионной среде, а затем энергия, переданная входящим светом, повторно излучалась — иногда на исходной частоте, но часто на двух более низких частотах, сумма которых равнялась исходной частоте. Согласно их модели, электрон , переведенный в более высокое энергетическое состояние путем принятия энергии входящего фотона, может вернуться за один шаг в свое положение равновесия, повторно излучая фотон той же частоты, или он может вернуться за более чем один шаг, излучая один фотон на каждый шаг при возвращении в свое состояние равновесия. Из-за того, как факторы сокращаются при выводе нового уравнения на основе этих соображений, результат оказывается относительно простым.
В рукопись также был включен коммутатор Гейзенберга , его закон умножения, необходимый для описания определенных свойств атомов, в соответствии с которыми произведение двух физических величин не коммутирует . Поэтому PQ будет отличаться от QP , где, например, P — импульс электрона, а Q — его положение. Поль Дирак , получивший пробный экземпляр в августе 1925 года, понял, что коммутативный закон не был полностью разработан, и он создал алгебраическую формулировку, чтобы выразить те же результаты в более логической форме. [14]
С помощью интенсивной серии математических аналогий, которые некоторые физики назвали «магическими», Гейзенберг выписал уравнение, которое является квантово-механическим аналогом для классического вычисления интенсивностей. Уравнение ниже представлено в статье. [15] [16] Его общая форма выглядит следующим образом:
Этот общий формат указывает, что некоторый термин C должен быть вычислен путем суммирования всех произведений некоторой группы терминов A на некоторую связанную группу терминов B. Потенциально будет существовать бесконечная серия терминов A и соответствующих им терминов B. Каждое из этих умножений имеет в качестве своих множителей два измерения, которые относятся к последовательным нисходящим переходам между энергетическими состояниями электрона. Этот тип правила отличает матричную механику от вида физики, знакомой в повседневной жизни, потому что важными значениями являются то, где (в каком энергетическом состоянии или «орбитали») электрон начинается и в каком энергетическом состоянии он заканчивается, а не то, что электрон делает, находясь в том или ином состоянии.
Например, если A и B оба ссылаются на списки частот, то расчет происходит следующим образом:
Умножьте частоту изменения энергии из состояния n в состояние n − a на частоту изменения энергии из состояния n − a в состояние n − b , и к этому прибавьте произведение, найденное путем умножения частоты изменения энергии из состояния n − a в состояние n − b на частоту изменения энергии из состояния n − b в состояние n − c , и т. д. Символически это выглядит так:
(Согласно используемому соглашению, n − a представляет собой более высокое энергетическое состояние, чем n , поэтому переход от n к n − a будет означать, что электрон принял энергию от входящего фотона и поднялся на более высокую орбиталь, тогда как переход от n − a к n будет означать, что электрон падает на более низкую орбиталь и испускает фотон.)
Было бы легко выполнить каждый отдельный шаг этого процесса для некоторой измеряемой величины. Например, формула в рамке в начале этой статьи дает каждую необходимую длину волны в последовательности. Вычисленные значения можно было бы очень легко заполнить в сетке, как описано ниже. Однако, поскольку ряд бесконечен, никто не мог выполнить весь набор вычислений.
Гейзенберг изначально придумал это уравнение, чтобы иметь возможность умножать два измерения одного и того же вида (амплитуды), поэтому не имело значения, в каком порядке они умножались. Однако Гейзенберг заметил, что если он попытается использовать ту же схему для умножения двух переменных, таких как импульс, p , и смещение, q , то «возникает значительная трудность». [17] Оказывается, что умножение матрицы p на матрицу q дает другой результат, чем умножение матрицы q на матрицу p . Это дает лишь крошечную разницу, но эта разница никогда не может быть уменьшена ниже определенного предела, и этот предел включает постоянную Планка , h . Подробнее об этом позже. Ниже приведен очень короткий пример того, что будут делать вычисления, помещенные в сетки, которые называются матрицами. Учитель Гейзенберга почти сразу понял, что его работа должна быть выражена в матричном формате, потому что математики уже были знакомы с тем, как выполнять вычисления с использованием матриц эффективным способом. (Поскольку Гейзенберг интересовался фотонным излучением, иллюстрации будут даны в терминах электронов, переходящих с более высокого энергетического уровня на более низкий уровень, например, n ← n − 1 , а не с более низкого уровня на более высокий уровень, например, n → n − 1 .) (уравнение для сопряженных переменных импульса и положения)
Матрица p
Матрица q
Матрица для произведения двух вышеуказанных матриц, как указано в соответствующем уравнении в статье Umdeutung , имеет вид
где
и так далее.
Если бы матрицы были перевернуты, то получились бы следующие значения:
и так далее.

Вернер Гейзенберг использовал идею о том, что поскольку классическая физика верна, когда она применяется к явлениям в мире вещей, больших, чем атомы и молекулы, она должна рассматриваться как частный случай более инклюзивной квантовой теоретической модели. Поэтому он надеялся, что сможет модифицировать квантовую физику таким образом, что когда параметры будут в масштабе повседневных объектов, она будет выглядеть так же, как классическая физика, но когда параметры будут сведены к атомному масштабу, разрывы, наблюдаемые в таких вещах, как широко разнесенные частоты видимого спектра яркой линии водорода, снова станут видны.
Единственное, что люди в то время больше всего хотели понять о водородном излучении, это как предсказать или учесть интенсивности линий в его спектре. Хотя Гейзенберг в то время этого не знал, общий формат, который он разработал для выражения своего нового способа работы с квантово-теоретическими вычислениями, может служить рецептом для двух матриц и того, как их умножать. [18]
В статье Umdeutung матрицы не упоминаются. Великим достижением Гейзенберга была «схема, которая в принципе была способна однозначно определять соответствующие физические качества (частоты переходов и амплитуды)» [19] водородного излучения.
После того, как Гейзенберг написал статью Umdeutung , он передал ее одному из своих старших коллег для внесения необходимых исправлений и ушел в отпуск. Макс Борн ломал голову над уравнениями и некоммутирующими уравнениями, которые Гейзенберг нашел проблемными и тревожными. Через несколько дней он понял, что эти уравнения представляют собой инструкции по написанию матриц. [20]
Рассмотрев ... примеры. .. [Гейзенберг] нашел это правило ... Это было летом 1925 года. Гейзенберг ... взял отпуск ... и передал мне свою статью для публикации ... Правило умножения Гейзенберга не оставляло меня в покое, и после недели интенсивных размышлений и проб я внезапно вспомнил алгебраическую теорию... Такие квадратичные массивы хорошо знакомы математикам и называются матрицами, в связи с определенным правилом умножения. Я применил это правило к квантовому условию Гейзенберга и обнаружил, что оно согласуется для диагональных элементов. Было легко догадаться, какими должны быть оставшиеся элементы, а именно, нулевыми; и тут же передо мной предстала странная формула
Символ Q — это матрица смещения, P — матрица импульса, i обозначает квадратный корень из отрицательной единицы , а h — постоянная Планка. [21] Борн и несколько его коллег взялись за задачу обработки всего в матричной форме до того, как Гейзенберг вернулся из отпуска, и через несколько месяцев новая квантовая механика в матричной форме легла в основу другой статьи. Это соотношение теперь известно как принцип неопределенности Гейзенберга .
Когда такие величины, как положение и импульс, упоминаются в контексте матричной механики Гейзенберга, такое утверждение, как pq ≠ qp, относится не к одному значению p и одному значению q, а к матрице (сетке значений, организованных определенным образом) значений положения и матрице значений импульса. Таким образом, умножение p на q или q на p на самом деле говорит о матричном умножении двух матриц. Когда две матрицы перемножаются, ответом является третья матрица.
Поль Дирак решил, что суть работы Гейзенберга заключается в той самой особенности, которую Гейзенберг изначально считал проблематичной – факте некоммутативности, например, между умножением матрицы импульса на матрицу смещения и умножением матрицы смещения на матрицу импульса. Это понимание привело Дирака в новых и продуктивных направлениях. [22]