Стандартная оценка

Сколько стандартных отклонений от среднего значения имеет наблюдаемый элемент данных?

Сравнение различных методов оценки в нормальном распределении , включая: стандартные отклонения , кумулятивные проценты, эквиваленты процентилей , z-оценки, T-оценки

В статистике стандартная оценка — это число стандартных отклонений , на которое значение сырой оценки (т. е. наблюдаемое значение или точка данных) выше или ниже среднего значения того, что наблюдается или измеряется. Сырые оценки выше среднего имеют положительные стандартные оценки, тогда как те, что ниже среднего, имеют отрицательные стандартные оценки.

Он рассчитывается путем вычитания среднего значения популяции из индивидуального сырого балла и последующего деления разницы на стандартное отклонение популяции . Этот процесс преобразования сырого балла в стандартный балл называется стандартизацией или нормализацией (однако «нормализация» может относиться ко многим типам соотношений; см. Нормализация для получения дополнительной информации).

Стандартные оценки чаще всего называются z -оценками ; эти два термина могут использоваться взаимозаменяемо, как в этой статье. Другие эквивалентные термины в использовании включают z-значение , z-статистику , нормальную оценку , стандартизированную переменную и тянуть в физике высоких энергий . ^{[1] [2]}

Для вычисления z-оценки необходимо знать среднее значение и стандартное отклонение всей совокупности, к которой принадлежит точка данных; если имеется только выборка наблюдений из совокупности, то аналогичное вычисление с использованием выборочного среднего значения и стандартного отклонения выборки дает t -статистику .

Расчет

Если известны среднее значение популяции и стандартное отклонение популяции, то исходный балл x преобразуется в стандартный балл по формуле ^[3]

${\displaystyle z={x-\mu \over \sigma }}$

где:

μ — среднее значение генеральной совокупности,

σ — стандартное отклонение генеральной совокупности.

Абсолютное значение z представляет собой расстояние между исходным баллом x и средним значением генеральной совокупности в единицах стандартного отклонения. z имеет отрицательное значение, если исходный балл ниже среднего значения, и положительное значение, если выше.

Расчет z с использованием этой формулы требует использования среднего значения популяции и стандартного отклонения популяции, а не среднего значения выборки или отклонения выборки. Однако знание истинного среднего значения и стандартного отклонения популяции часто является нереалистичным ожиданием, за исключением таких случаев, как стандартизированное тестирование , когда измеряется вся популяция.

Если среднее значение совокупности и стандартное отклонение совокупности неизвестны, стандартную оценку можно оценить, используя среднее значение выборки и стандартное отклонение выборки в качестве оценок значений совокупности. ^{[4] [5] [6] [7]}

В этих случаях z -оценка определяется как

${\displaystyle z={x-{\bar {x}} \over S}}$

где:

${\displaystyle {\bar {x}}}$это среднее значение выборки,

S — стандартное отклонение выборки.

Хотя это всегда следует указывать, различие между использованием статистики населения и выборки часто не проводится. В любом случае числитель и знаменатель уравнений имеют одинаковые единицы измерения, так что единицы сокращаются посредством деления, и z остается как безразмерная величина .

Приложения

Z-тест

Z-оценка часто используется в z-тесте в стандартизированном тестировании – аналоге t-теста Стьюдента для популяции, параметры которой известны, а не оценены. Поскольку очень необычно знать всю популяцию, t-тест используется гораздо шире.

Интервалы прогнозирования

Стандартная оценка может быть использована при расчете интервалов прогнозирования . Интервал прогнозирования [ L , U ], состоящий из нижней конечной точки, обозначенной L , и верхней конечной точки, обозначенной U , представляет собой интервал, такой, что будущее наблюдение X будет лежать в интервале с высокой вероятностью , т.е. ${\displaystyle \gamma }$

${\displaystyle P(L<X<U)=\gamma ,}$

Для стандартной оценки Z из X это дает: ^[8]

${\displaystyle P\left({\frac {L-\mu }{\sigma }}<Z<{\frac {U-\mu }{\sigma }}\right)=\gamma .}$

Определив квантиль z таким образом, что

${\displaystyle P\left(-z<Z<z\right)=\gamma }$

следует:

${\displaystyle L=\mu -z\sigma ,\ U=\mu +z\sigma }$

Управление процессом

В приложениях управления технологическими процессами значение Z позволяет оценить степень отклонения процесса от целевого значения.

Сравнение результатов, полученных по разным шкалам: ACT и SAT

Z - оценка для студента A составила 1, что означает, что студент A был на 1 стандартное отклонение выше среднего. Таким образом, студент A показал результат в 84,13 процентиля на SAT.

Когда баллы измеряются по разным шкалам, их можно преобразовать в z-баллы для облегчения сравнения. Диц и др. ^[9] приводят следующий пример, сравнивая баллы учащихся по (старым) тестам SAT и ACT для старших классов. В таблице показано среднее значение и стандартное отклонение для общих баллов по SAT и ACT. Предположим, что ученик A набрал 1800 баллов по SAT, а ученик B набрал 24 балла по ACT. Какой ученик показал лучшие результаты по сравнению с другими сдающими тест?

Z - оценка для студента B составила 0,6, что означает, что студент B был на 0,6 стандартного отклонения выше среднего. Таким образом, студент B показал результат в 72,57 процентиля на SAT.

Z-оценка для студента А составляет ${\displaystyle z={x-\mu \over \sigma }={1800-1500 \over 300}=1}$

Z-оценка для студента B составляет ${\displaystyle z={x-\mu \over \sigma }={24-21 \over 5}=0.6}$

Поскольку у студента А z-балл выше, чем у студента Б, студент А показал лучшие результаты по сравнению с другими сдающими тест, чем студент Б.

Процент наблюдений ниже z-оценки

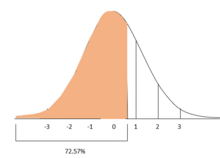
Продолжая пример с результатами ACT и SAT, если можно предположить, что результаты ACT и SAT распределены нормально (что приблизительно верно), то z-оценки можно использовать для расчета процента сдающих тест, получивших более низкие баллы, чем студенты A и B.

Кластерный анализ и многомерное шкалирование

«Для некоторых многомерных методов, таких как многомерное шкалирование и кластерный анализ, концепция расстояния между единицами данных часто представляет значительный интерес и важность… Когда переменные в многомерном наборе данных находятся в разных масштабах, имеет больше смысла вычислять расстояния после некоторой формы стандартизации». ^[10]

Анализ главных компонент

В анализе главных компонентов «переменные, измеряемые в разных шкалах или в общей шкале с сильно различающимися диапазонами, часто стандартизируются» ^{[11] .}

Относительная важность переменных во множественной регрессии: стандартизированные коэффициенты регрессии

Стандартизация переменных перед множественным регрессионным анализом иногда используется в качестве вспомогательного средства для интерпретации. ^[12] (стр. 95) утверждает следующее.

«Стандартизированный наклон регрессии — это наклон в уравнении регрессии, если X и Y стандартизированы… Стандартизация X и Y выполняется путем вычитания соответствующих средних значений из каждого набора наблюдений и деления на соответствующие стандартные отклонения… В множественной регрессии, где используются несколько переменных X, стандартизированные коэффициенты регрессии количественно определяют относительный вклад каждой переменной X».

Однако Катнер и др. ^[13] (стр. 278) делают следующее предостережение: «… следует проявлять осторожность при интерпретации любых коэффициентов регрессии, независимо от того, стандартизированы они или нет. Причина в том, что когда предикторные переменные коррелируют между собой, … на коэффициенты регрессии влияют другие предикторные переменные в модели… Величины стандартизированных коэффициентов регрессии зависят не только от наличия корреляций между предикторными переменными, но и от интервалов между наблюдениями по каждой из этих переменных. Иногда эти интервалы могут быть совершенно произвольными. Следовательно, обычно неразумно интерпретировать величины стандартизированных коэффициентов регрессии как отражающие сравнительную важность предикторных переменных».

Стандартизация в математической статистике

В математической статистике случайная величина X стандартизируется путем вычитания ее ожидаемого значения и деления разницы на ее стандартное отклонение. ${\displaystyle \operatorname {E} [X]}$ ${\displaystyle \sigma (X)={\sqrt {\operatorname {Var} (X)}}:}$

${\displaystyle Z={X-\operatorname {E} [X] \over \sigma (X)}}$

Если рассматриваемая случайная величина является выборочным средним случайной выборки X : ${\displaystyle \ X_{1},\dots ,X_{n}}$

${\displaystyle {\bar {X}}={1 \over n}\sum _{i=1}^{n}X_{i}}$

то стандартизированная версия

${\displaystyle Z={\frac {{\bar {X}}-\operatorname {E} [{\bar {X}}]}{\sigma (X)/{\sqrt {n}}}}}$

Где стандартизированная дисперсия выборочного среднего рассчитывалась следующим образом:

${\displaystyle {\begin{array}{l}\operatorname {Var} \left(\sum x_{i}\right)=\sum \operatorname {Var} (x_{i})=n\operatorname {Var} (x_{i})=n\sigma ^{2}\\\operatorname {Var} ({\overline {X}})=\operatorname {Var} \left({\frac {\sum x_{i}}{n}}\right)={\frac {1}{n^{2}}}\operatorname {Var} \left(\sum x_{i}\right)={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}\end{array}}}$

T-оценка

В образовательной оценке T-балл представляет собой стандартный балл, смещенный по оси Z и масштабированный так, чтобы среднее значение было равно 50, а стандартное отклонение — 10. ^{[14] [15] [16]} В Японии он также известен как хэнсачи , где эта концепция гораздо более широко известна и используется в контексте приема в старшие классы и университеты.

При измерении плотности костей Т-показатель является стандартным показателем измерения по сравнению с популяцией здоровых 30-летних взрослых и имеет обычное среднее значение 0 и стандартное отклонение 1. ^[17]

Смотрите также

• Функция ошибки
• Расстояние Махаланобиса
• Нормализация (статистика)
• Коэффициент омега
• Стандартное нормальное отклонение
• Студенизированный остаток

Ссылки

1. Mulders, Martijn; Zanderighi, Giulia, ред. (2017). Европейская школа физики высоких энергий 2015: Банско, Болгария 02 - 15 сентября 2015 г. CERN Yellow Reports: Труды школы. Женева: CERN. ISBN 978-92-9083-472-4.
2. Гросс, Эйлам (2017-11-06). «Практическая статистика для физики высоких энергий». CERN Yellow Reports: School Proceedings . 4/2017: 165–186. doi :10.23730/CYRSP-2017-004.165.
3. E. Kreyszig (1979). Advanced Engineering Mathematics (Четвертое изд.). Wiley. стр. 880, ур. 5. ISBN 0-471-02140-7.
4. Спигель, Мюррей Р.; Стивенс, Ларри Дж. (2008), Статистика Шаума (четвертое издание), McGraw Hill, ISBN 978-0-07-148584-5
5. Менденхолл, Уильям; Синчич, Терри (2007), Статистика для инженерии и наук (Пятое издание), Pearson / Prentice Hall, ISBN 978-0131877061
6. Гланц, Стэнтон А.; Слинкер, Брайан К.; Нейландс, Торстен Б. (2016), Primer of Applied Regression & Variance Analysis (третье изд.), McGraw Hill, ISBN 978-0071824118
7. Ахо, Кен А. (2014), Фундаментальная и прикладная статистика для биологов (первое издание), Chapman & Hall / CRC Press, ISBN 978-1439873380
8. E. Kreyszig (1979). Advanced Engineering Mathematics (Четвертое изд.). Wiley. стр. 880, ур. 6. ISBN 0-471-02140-7.
9. Диез, Дэвид; Барр, Кристофер; Четинкая-Рундель, Майн (2012), OpenIntro Statistics (Второе издание), openintro.org
10. Эверитт, Брайан; Хоторн, Торстен Дж. (2011), Введение в прикладной многомерный анализ с R , Springer, ISBN 978-1441996497
11. Джонсон, Ричард; Вихерн, Вихерн (2007), Прикладной многомерный статистический анализ , Pearson / Prentice Hall
12. Афифи, Абдельмонем; Мэй, Сюзанна К.; Кларк, Вирджиния А. (2012), Практический многомерный анализ (пятое изд.), Chapman & Hall/CRC, ISBN 978-1439816806
13. Катнер, Михаэль; Нахтсхайм, Кристофер; Нетер, Джон (204), Прикладные линейные регрессионные модели (четвертое издание), McGraw Hill, ISBN 978-0073014661
14. Джон Сальвия; Джеймс Исселдайк; Сара Уитмер (29 января 2009 г.). Оценка: в специальном и инклюзивном образовании. Cengage Learning. стр. 43–. ISBN 978-0-547-13437-6.
15. Эдвард С. Нойкруг; Р. Чарльз Фосетт (1 января 2014 г.). Основы тестирования и оценки: практическое руководство для консультантов, социальных работников и психологов. Cengage Learning. стр. 133–. ISBN 978-1-305-16183-2.
16. Рэнди В. Кампхаус (16 августа 2005 г.). Клиническая оценка интеллекта детей и подростков. Springer. стр. 123–. ISBN 978-0-387-26299-4.
17. "Измерение костной массы: что означают цифры". Национальный центр ресурсов по остеопорозу и связанным с ним заболеваниям костей NIH . Национальный институт здравоохранения . Получено 5 августа 2017 г.

Дальнейшее чтение

• Кэрролл, Сьюзен Ровецци; Кэрролл, Дэвид Дж. (2002). Статистика, упрощенная для руководителей школ (иллюстрированное издание). Rowman & Littlefield. ISBN 978-0-8108-4322-6. Получено 7 июня 2009 г.
• Ларсен, Ричард Дж.; Маркс, Моррис Л. (2000). Введение в математическую статистику и ее приложения (третье изд.). стр. 282. ISBN 0-13-922303-7.

Внешние ссылки

• калькулятор z-оценки