В математике теория катастроф является разделом теории бифуркаций при изучении динамических систем ; она также является частным случаем более общей теории особенностей в геометрии .
Теория бифуркации изучает и классифицирует явления, характеризующиеся внезапными изменениями в поведении, возникающими из-за небольших изменений обстоятельств, анализируя, как качественная природа решений уравнений зависит от параметров, которые появляются в уравнении. Это может привести к внезапным и драматическим изменениям, например , непредсказуемым срокам и величине оползня .
Теория катастроф возникла в результате работы французского математика Рене Тома в 1960-х годах и стала очень популярной благодаря усилиям Кристофера Зеемана в 1970-х годах. Она рассматривает особый случай, когда долгосрочное устойчивое равновесие может быть идентифицировано как минимум гладкой, четко определенной потенциальной функции ( функции Ляпунова ). Небольшие изменения определенных параметров нелинейной системы могут привести к появлению или исчезновению равновесий или к изменению их с притяжения на отталкивание и наоборот, что приводит к большим и внезапным изменениям поведения системы. Однако, рассмотренная в более широком пространстве параметров , теория катастроф показывает, что такие точки бифуркации имеют тенденцию возникать как часть четко определенных качественных геометрических структур.
В конце 1970-х годов приложения теории катастроф к областям, выходящим за рамки ее компетенции, начали подвергаться критике, особенно в биологии и социальных науках. [1] [2] Залер и Сассманн в статье 1977 года в журнале Nature назвали такие приложения «характеризующимися неверными рассуждениями, надуманными предположениями, ошибочными следствиями и преувеличенными утверждениями». [3] В результате теория катастроф стала менее популярной в приложениях. [4]
Теория катастроф анализирует вырожденные критические точки потенциальной функции — точки, в которых не только первая производная, но и одна или несколько высших производных потенциальной функции также равны нулю. Они называются ростками геометрий катастроф. Вырождение этих критических точек можно раскрыть , разложив потенциальную функцию в ряд Тейлора по малым возмущениям параметров.
Когда вырожденные точки не просто случайны, а структурно устойчивы , вырожденные точки существуют как организующие центры для конкретных геометрических структур более низкой вырожденности с критическими характеристиками в пространстве параметров вокруг них. Если потенциальная функция зависит от двух или менее активных переменных и четырех или менее активных параметров, то существует только семь общих структур для этих бифуркационных геометрий с соответствующими стандартными формами, в которые ряд Тейлора вокруг зародышей катастроф может быть преобразован диффеоморфизмом ( гладким преобразованием, обратное которому также является гладким). [ необходима цитата ] Эти семь фундаментальных типов теперь представлены с названиями, которые им дал Том.
Теория катастроф изучает динамические системы, которые описывают эволюцию [5] переменной состояния с течением времени :
В приведенном выше уравнении называется потенциальной функцией и часто является вектором или скаляром, который параметризует потенциальную функцию. Значение может меняться со временем, и его также можно называть управляющей переменной. В следующих примерах такими элементами управления являются такие параметры, как .


Когда a < 0 , потенциал V имеет два экстремума — один устойчивый и один неустойчивый. Если параметр a медленно увеличивается, система может следовать за точкой устойчивого минимума. Но при a = 0 устойчивый и неустойчивый экстремумы встречаются и аннигилируют. Это точка бифуркации. При a > 0 устойчивого решения больше нет. Если проследить физическую систему через бифуркацию складки, то можно обнаружить, что когда a достигает 0, устойчивость решения a < 0 внезапно теряется, и система совершит внезапный переход к новому, совершенно иному поведению. Это бифуркационное значение параметра a иногда называют « точкой перелома ».
Геометрия каспа очень распространена, когда исследуется, что происходит с бифуркацией складки, если к пространству управления добавляется второй параметр, b . Изменяя параметры, можно обнаружить, что теперь есть кривая (синяя) точек в пространстве ( a , b ), где стабильность теряется, где устойчивое решение внезапно перейдет к альтернативному результату.
Но в геометрии каспа бифуркационная кривая замыкается сама на себя, давая вторую ветвь, где это альтернативное решение само теряет устойчивость и совершает скачок назад к исходному набору решений. Многократно увеличивая b , а затем уменьшая его, можно, таким образом, наблюдать петли гистерезиса , поскольку система попеременно следует одному решению, переходит к другому, следует за другим обратно, а затем переходит обратно к первому.
Однако это возможно только в области пространства параметров a < 0. По мере увеличения a петли гистерезиса становятся все меньше и меньше, пока выше a = 0 они не исчезнут совсем (катастрофа возврата), и остается только одно устойчивое решение.
Можно также рассмотреть, что произойдет, если удерживать b постоянным и изменять a . В симметричном случае b = 0 можно наблюдать бифуркацию вилки при уменьшении a , при этом одно устойчивое решение внезапно расщепляется на два устойчивых решения и одно неустойчивое решение, когда физическая система переходит к a < 0 через точку возврата (0,0) (пример спонтанного нарушения симметрии ). Вдали от точки возврата нет никаких внезапных изменений в отслеживаемом физическом решении: при прохождении через кривую бифуркаций складок все, что происходит, — это становится доступным альтернативное второе решение.
Известное предположение заключается в том, что катастрофу каспа можно использовать для моделирования поведения стрессовой собаки, которая может реагировать, становясь запуганной или разгневанной. [6] Предполагается, что при умеренном стрессе ( a > 0 ) собака будет демонстрировать плавный переход реакции от запуганной к злой, в зависимости от того, как ее спровоцировали. Но более высокие уровни стресса соответствуют переходу в область ( a < 0 ). Затем, если собака начинает запуганной, она будет оставаться запуганной, поскольку ее раздражают все больше и больше, пока она не достигнет точки «сгиба», когда она внезапно, прерывисто перейдет в режим злости. Оказавшись в режиме «злости», она будет оставаться злой, даже если параметр прямого раздражения значительно снижен.
Простая механическая система, «Машина катастроф Зеемана», прекрасно иллюстрирует катастрофу каспа. В этом устройстве плавные изменения положения конца пружины могут вызывать внезапные изменения положения вращения прикрепленного колеса. [7]
Катастрофический отказ сложной системы с параллельным резервированием можно оценить на основе соотношения между локальными и внешними напряжениями. Модель механики структурного разрушения похожа на поведение катастрофы каспа. Модель предсказывает резервную способность сложной системы.
Другие приложения включают перенос электронов во внешней сфере, часто встречающийся в химических и биологических системах, [8] моделирование динамики ядер конденсации облаков в атмосфере, [9] и моделирование цен на недвижимость. [10]
Бифуркации складок и геометрия каспа являются, безусловно, наиболее важными практическими следствиями теории катастроф. Это закономерности, которые снова и снова повторяются в физике, инженерии и математическом моделировании. Они производят сильные события гравитационного линзирования и предоставляют астрономам один из методов, используемых для обнаружения черных дыр и темной материи Вселенной, посредством явления гравитационного линзирования, производящего множественные изображения далеких квазаров . [11]
Остальные простые геометрии катастроф весьма специфичны в сравнении и представлены здесь только из любопытства.


Пространство параметров управления трехмерно. Бифуркационное множество в пространстве параметров состоит из трех поверхностей бифуркаций складок, которые встречаются в двух линиях бифуркаций каспов, которые в свою очередь встречаются в одной точке бифуркации ласточкин хвост.
По мере того как параметры проходят через поверхность бифуркаций складок, один минимум и один максимум потенциальной функции исчезают. В точках бифуркации возврата два минимума и один максимум заменяются одним минимумом; за ними бифуркации возврата исчезают. В точке ласточкина хвоста два минимума и два максимума встречаются при одном значении x . Для значений a > 0 за пределами ласточкина хвоста существует либо одна пара максимум-минимум, либо их вообще нет, в зависимости от значений b и c . Две поверхности бифуркаций складок и две линии бифуркаций возврата, где они встречаются при a < 0 , поэтому исчезают в точке ласточкина хвоста, чтобы замениться только одной поверхностью бифуркаций возврата. Последняя картина Сальвадора Дали «Хвост ласточки » была основана на этой катастрофе.

В зависимости от значений параметров, потенциальная функция может иметь три, два или один различных локальных минимума, разделенных локусами бифуркаций складок. В точке бабочки различные 3-поверхности бифуркаций складок, 2-поверхности бифуркаций каспов и линии бифуркаций ласточкина хвоста встречаются и исчезают, оставляя единственную структуру каспа, когда a > 0 .


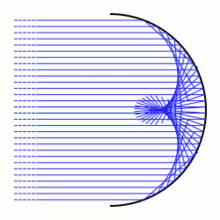
Умбиликальные катастрофы являются примерами катастроф corank 2. Их можно наблюдать в оптике в фокальных поверхностях, созданных светом, отражающимся от поверхности в трех измерениях, и они тесно связаны с геометрией почти сферических поверхностей: umbilical point . Том предположил, что гиперболическая umbilic катастрофа моделирует разрушение волны, а эллиптическая umbilic моделирует создание структур, похожих на волосы.
Владимир Арнольд дал катастрофам классификацию ADE из-за их глубокой связи с простыми группами Ли . [ необходима ссылка ]
В теории особенностей существуют объекты, которые соответствуют большинству других простых групп Ли.

Как предсказывает теория катастроф, сингулярности являются общими и устойчивыми к возмущениям. Это объясняет, как яркие линии и поверхности устойчивы к возмущениям. Каустики, которые можно увидеть на дне бассейна, например, имеют отличительную текстуру и имеют только несколько типов сингулярных точек, хотя поверхность воды постоянно меняется. [12]
Например, край радуги имеет катастрофу сгиба. Из-за волновой природы света катастрофа имеет тонкие детали дифракции, описываемые функцией Эйри . Это общий результат, не зависящий от точной формы капли воды, поэтому край радуги всегда имеет форму функции Эйри. [13] [14] Ту же самую катастрофу сгиба функции Эйри можно увидеть в ядерно-ядерном рассеянии («ядерная радуга»). [15]
Катастрофа каспа является следующей по простоте наблюдения. Из-за волновой природы света катастрофа имеет тонкие дифракционные детали, описываемые функцией Пирси . [16] Также наблюдались катастрофы более высокого порядка, такие как ласточкин хвост и бабочка. [17]