Непрерывная или дискретная переменная

Типы количественных переменных в математике

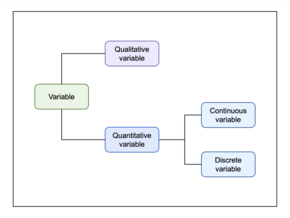
В математике и статистике количественная переменная может быть непрерывной или дискретной , если они обычно получаются путем измерения или подсчета соответственно. ^[1] Если она может принимать два конкретных действительных значения таким образом, что она также может принимать все действительные значения между ними (включая значения, которые произвольно или бесконечно близки друг к другу), то переменная непрерывна в этом интервале . ^[2] Если она может принимать значение такое, что с каждой стороны от нее имеется не бесконечно малый промежуток, не содержащий значений, которые переменная может принимать, то она дискретна вокруг этого значения. ^[3] В некоторых контекстах переменная может быть дискретной в одних диапазонах числовой прямой и непрерывной в других.

Переменные можно разделить на две основные категории: качественные (категориальные) и количественные (числовые). Непрерывные и дискретные переменные являются подкатегориями количественных переменных. Обратите внимание, что эта схема не является исчерпывающей с точки зрения типов переменных.

Непрерывная переменная

Непрерывная переменная — это переменная, между любыми двумя значениями которой существуют возможные значения.

Например, переменная в непустом диапазоне действительных чисел является непрерывной, если она может принимать любое значение в этом диапазоне. ^[4]

Методы исчисления часто используются в задачах, в которых переменные являются непрерывными, например, в задачах непрерывной оптимизации . ^[5]

В статистической теории распределения вероятностей непрерывных переменных можно выразить через функции плотности вероятности . ^[6]

В непрерывной динамике переменная времени рассматривается как непрерывная, а уравнение, описывающее эволюцию некоторой переменной с течением времени, является дифференциальным уравнением . ^[7] Мгновенная скорость изменения — это четко определенное понятие, которое берет отношение изменения зависимой переменной к независимой переменной в определенный момент времени.

Это изображение флаконов с разным количеством жидкости. Непрерывной переменной может быть объем жидкости в флаконах. Дискретной переменной может быть количество флаконов.

Дискретная переменная

Напротив, переменная является дискретной переменной тогда и только тогда, когда существует однозначное соответствие между этой переменной и подмножеством , множеством натуральных чисел . ^[8] Другими словами, дискретная переменная в определенном интервале действительных значений — это та, для которой для любого значения в диапазоне, который разрешено принимать переменной, существует положительное минимальное расстояние до ближайшего другого допустимого значения. Значение дискретной переменной может быть получено путем подсчета, а число допустимых значений либо конечно, либо счетно бесконечно . Обычными примерами являются переменные, которые должны быть целыми числами , неотрицательными целыми числами, положительными целыми числами или только целыми числами 0 и 1. ^[9] ${\displaystyle \mathbb {N} }$

Методы исчисления не всегда подходят для решения задач с дискретными переменными. Особенно в многомерном исчислении многие модели полагаются на предположение о непрерывности. ^[10] Примерами задач с дискретными переменными являются целочисленное программирование .

В статистике распределения вероятностей дискретных переменных можно выразить через функции масс вероятности . ^[6]

В динамике дискретного времени переменная времени рассматривается как дискретная, а уравнение эволюции некоторой переменной во времени называется разностным уравнением . ^[11] Для некоторых динамических систем с дискретным временем реакция системы может быть смоделирована путем решения разностного уравнения для аналитического решения.

В эконометрике и, в более общем плане, в регрессионном анализе иногда некоторые переменные, эмпирически связанные друг с другом, являются переменными 0-1, которым разрешено принимать только эти два значения. ^[12] Целью дискретных значений 0 и 1 является использование фиктивной переменной в качестве «переключателя», который может «включаться» и «выключаться» путем присвоения двух значений различным параметрам в уравнении. Переменная такого типа называется фиктивной переменной . Если зависимая переменная является фиктивной переменной, то обычно используется логистическая регрессия или пробит-регрессия . В случае регрессионного анализа фиктивная переменная может использоваться для представления подгрупп выборки в исследовании (например, значение 0 соответствует компоненту контрольной группы). ^[13]

Смесь непрерывных и дискретных переменных

Смешанная многомерная модель может содержать как дискретные, так и непрерывные переменные. Например, простая смешанная многомерная модель может иметь дискретную переменную , которая принимает только значения 0 или 1, и непрерывную переменную . ^[14] Примером смешанной модели может быть исследование риска психологических расстройств, основанное на одной бинарной мере психиатрических симптомов и одной непрерывной мере когнитивной деятельности. ^[15] Смешанные модели могут также включать одну переменную, которая является дискретной в некотором диапазоне числовой прямой и непрерывной в другом диапазоне. ${\displaystyle x}$ ${\displaystyle y}$

В теории вероятностей и статистике распределение вероятностей смешанной случайной величины состоит как из дискретных, так и из непрерывных компонентов. Смешанная случайная величина не имеет кумулятивной функции распределения , которая является дискретной или всюду непрерывной. Примером случайной величины смешанного типа является вероятность времени ожидания в очереди. Вероятность того, что клиент испытает нулевое время ожидания, является дискретной, в то время как ненулевое время ожидания оценивается в непрерывной шкале времени. ^[16] В физике (особенно в квантовой механике, где часто возникает этот вид распределения) дельта-функции Дирака часто используются для обработки непрерывных и дискретных компонентов единым образом. Например, предыдущий пример может быть описан плотностью вероятности , такой что , и . ${\displaystyle p(t)=\alpha \delta (t)+g(t)}$ ${\displaystyle P(t>0)=\int _{0}^{\infty }g(t)=1-\alpha }$ ${\displaystyle P(t=0)=\alpha }$

Смотрите также

• Непрерывный или дискретный спектр
• Непрерывная функция
• Подсчет данных
• Дискретная математика
• Непрерывный спектр
• Дискретный спектр
• Дискретное время и непрерывное время
• Непрерывный во времени случайный процесс
• Стохастический процесс с дискретным временем
• Непрерывное моделирование
• Дискретное моделирование
• Непрерывная геометрия
• Дискретная геометрия
• Непрерывное представление ряда
• Представление дискретного ряда
• Дискретизация
• Интерполяция
• Дискретная мера
• Дискретное пространство

Ссылки

1. Али, Зульфикар; Бхаскар, С. Бала (сентябрь 2016 г.). «Основные статистические инструменты в исследованиях и анализе данных». Indian Journal of Anaesthesia . 60 (9): 662–669. doi : 10.4103/0019-5049.190623 . PMC  5037948. PMID  27729694 .
2. Калиядан, Ферозе; Кулкарни, Винай (январь 2019 г.). «Типы переменных, описательная статистика и размер выборки». Indian Dermatology Online Journal . 10 (1): 82–86. doi : 10.4103/idoj.IDOJ_468_18 . PMC 6362742. PMID  30775310 . 
3. К. Д. Джоши, Основы дискретной математики , 1989, New Age International Limited, [1], стр. 7.
4. Brzychczy, Stanisaw; Gorniewicz, Lech (2011). «Непрерывные и дискретные модели нейронных систем в бесконечномерных абстрактных пространствах». Neurocomputing . 74 (17): 2711–2715. doi :10.1016/j.neucom.2010.11.005.
5. Грива, Игорь; Нэш, Стивен; Софер, Ариэла (2009). Линейная и нелинейная оптимизация (2-е изд.). Филадельфия: Общество промышленной и прикладной математики. п. 7. ISBN 978-0-89871-661-0. OCLC  236082842.
6. Деккинг, Фредерик Мишель; Краайкамп, Корнелис; Лопухаа, Хендрик Пауль; Местер, Людольф Эрвин (2005). «Современное введение в вероятность и статистику». Спрингеровские тексты в статистике . дои : 10.1007/1-84628-168-7. ISBN 978-1-85233-896-1. ISSN  1431-875X.
7. Poyton, AA; Varziri, Mohammad Saeed; McAuley, Kimberley B.; MclellanPat James, Pat James; Ramsay, James O. (15 февраля 2006 г.). «Оценка параметров в динамических моделях с непрерывным временем с использованием главного дифференциального анализа». Computers & Chemical Engineering . 30 (4): 698–708. doi :10.1016/j.compchemeng.2005.11.008.
8. Одифредди, Пьерджорджио (18 февраля 1992 г.). Классическая теория рекурсии: теория функций и множеств натуральных чисел . North Holland Publishing Company. стр. 18. ISBN 978-0444894830.
9. ван Даувен, Эрик (1984). Справочник по теоретико-множественной топологии . Северная Голландия: Elsevier. С. 113–167. ISBN 978-0-444-86580-9.
10. Клогг, Клиффорд К.; Шокей, Джеймс У. (1988). Справочник по многомерной экспериментальной психологии . Бостон, Массачусетс: Springer Publishing Company. стр. 337–365. ISBN 978-1-4613-0893-5.
11. Thyagarajan, KS (2019). Введение в цифровую обработку сигналов с использованием MATLAB с применением к цифровой связи (1-е изд.). Springer Publishing Company. стр. 21–63. ISBN 978-3319760285.
12. Миллер, Джерри Л. Л.; Эриксон, Мейнард Л. (май 1974 г.). «О регрессионном анализе фиктивных переменных». Социологические методы и исследования . 2 (4): 395–519. doi :10.1177/004912417400200402.
13. Харди, Мелисса А. (25 февраля 1993 г.). Регрессия с фиктивными переменными (количественные применения в социальных науках) (1-е изд.). Newbury Park: Sage Publications, Inc. стр. v. ISBN 0803951280.
14. Олкин, Ингрэм; Тейт, Роберт (июнь 1961 г.). «Многомерные корреляционные модели со смешанными дискретными и непрерывными переменными». Анналы математической статистики . 32 (2): 448–465. doi : 10.1214/aoms/1177705052 .
15. Фицморис, Гарретт М.; Лэрд, Нэн М. (март 1997 г.). «Регрессионные модели для смешанных дискретных и непрерывных ответов с потенциально пропущенными значениями». Биометрия . 53 (1): 110–122. doi :10.2307/2533101. JSTOR  2533101.
16. Шарма, Шалендра Д. (март 1975 г.). «О непрерывной/дискретной системе очередей с прибытием партиями переменного размера и коррелированными отправлениями». Журнал прикладной вероятности . 12 (1): 115–129. doi :10.2307/3212413. JSTOR  3212413.