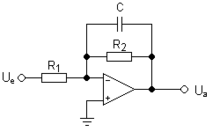
Топология электронного фильтра

Топология электронного фильтра определяет схемы электронного фильтра, не принимая во внимание значения используемых компонентов, а только способ соединения этих компонентов.

Конструкция фильтра характеризует схемы фильтров в первую очередь их передаточной функцией , а не топологией . Передаточные функции могут быть линейными или нелинейными . Распространенными типами передаточной функции линейного фильтра являются: высокочастотный , низкочастотный , полосовой , режекторный или режекторный и всепроходной . После выбора передаточной функции для фильтра можно выбрать конкретную топологию для реализации такого прототипа фильтра , например, можно выбрать проектирование фильтра Баттерворта с использованием топологии Саллена–Ки .

Топологии фильтров можно разделить на пассивные и активные типы. Пассивные топологии состоят исключительно из пассивных компонентов : резисторов, конденсаторов и индукторов. Активные топологии также включают активные компоненты (такие как транзисторы, операционные усилители и другие интегральные схемы), которым требуется питание. Кроме того, топологии могут быть реализованы либо в несбалансированной форме, либо в сбалансированной форме при использовании в сбалансированных схемах . Такие реализации, как электронные микшеры и стереозвук, могут потребовать массивов идентичных схем.

Пассивные топологии

Пассивные фильтры давно разрабатываются и используются . Большинство из них построены из простых двухпортовых сетей, называемых «секциями». Не существует формального определения секции, за исключением того, что она должна иметь по крайней мере один последовательный компонент и один шунтирующий компонент. Секции неизменно соединены в топологию «каскада» или «цепочки» , состоящей из дополнительных копий той же секции или совершенно разных секций. Правила последовательного и параллельного импеданса объединяют две секции, состоящие только из последовательных компонентов или шунтирующих компонентов, в одну секцию.

Некоторые пассивные фильтры, состоящие только из одной или двух фильтрующих секций, имеют специальные названия, включая L-секцию, T-секцию и Π-секцию, которые являются несбалансированными фильтрами, а также C-секцию, H-секцию и коробчатую секцию, которые являются сбалансированными. Все они построены на очень простой топологии "лестницы" (см. ниже). Таблица внизу страницы показывает эти различные топологии в терминах общих постоянных k-фильтров .

Фильтры, разработанные с использованием сетевого синтеза, обычно повторяют простейшую форму топологии L-секции, хотя значения компонентов могут меняться в каждой секции. Фильтры, разработанные с помощью изображений , с другой стороны, сохраняют те же основные значения компонентов от секции к секции, хотя топология может меняться и, как правило, использовать более сложные секции.

Г-образные сечения никогда не бывают симметричными, но два Г-образных сечения, соединенные спина к спине, образуют симметричную топологию, а многие другие сечения имеют симметричную форму.

Топологии лестничного типа

Лестничная топология, часто называемая топологией Кауэра в честь Вильгельма Кауэра (изобретателя эллиптического фильтра ), на самом деле была впервые использована Джорджем Кэмпбеллом (изобретателем фильтра с постоянным k ). Кэмпбелл опубликовал свою работу в 1922 году, но, очевидно, использовал эту топологию уже некоторое время до этого. Кауэр впервые взялся за лестницы (опубликовано в 1926 году), вдохновленный работой Фостера (1924). Существует две формы основных лестничных топологий: несбалансированная и сбалансированная. Топологию Кауэра обычно считают несбалансированной лестничной топологией.

Лестничная сеть состоит из каскадных асимметричных L-секций (несбалансированных) или C-секций (сбалансированных). В форме нижних частот топология будет состоять из последовательных индукторов и шунтирующих конденсаторов. Другие формы полос будут иметь столь же простую топологию, преобразованную из топологии нижних частот. Преобразованная сеть будет иметь шунтирующие проводимости, которые являются двойными сетями последовательных импедансов, если они были двойными в исходной сети - что имеет место в случае последовательных индукторов и шунтирующих конденсаторов.

Модифицированные лестничные топологии

Конструкция фильтра изображения обычно использует модификации базовой топологии лестницы. Эти топологии, изобретенные Отто Цобелем ^[1], имеют те же полосы пропускания , что и лестница, на которой они основаны, но их передаточные функции изменены для улучшения некоторых параметров, таких как согласование импеданса , подавление полосы пропускания или крутизна перехода из полосы пропускания в полосу задерживания. Обычно конструкция применяет некоторое преобразование к простой топологии лестницы: результирующая топология похожа на лестницу, но больше не подчиняется правилу, согласно которому проводимости шунта являются двойной сетью последовательных импедансов: она неизменно становится более сложной с большим количеством компонентов. Такие топологии включают:

Фильтр m-типа (m-производный) на сегодняшний день является наиболее часто используемой модифицированной топологией лестничного изображения. Для каждой из основных топологий лестничного изображения существует две топологии m-типа; топологии последовательного и шунтового происхождения. Они имеют идентичные передаточные функции друг для друга, но разные импедансы изображения. Если фильтр проектируется с более чем одной полосой пропускания, топология m-типа приведет к фильтру, в котором каждая полоса пропускания имеет аналогичный отклик в частотной области. Можно обобщить топологию m-типа для фильтров с более чем одной полосой пропускания, используя параметры m ₁ , m ₂ , m ₃ и т. д., которые не равны друг другу, что приводит к общим фильтрам m _n -типа ^[2] , которые имеют формы полос, которые могут различаться в разных частях частотного спектра.

Топологию mm'-типа можно рассматривать как конструкцию двойного m-типа. Как и m-тип, она имеет ту же форму полосы, но предлагает улучшенные характеристики передачи. Однако это редко используемая конструкция из-за увеличенного количества компонентов и сложности, а также из-за того, что она обычно требует базовых секций лестничного типа и m-типа в одном фильтре для согласования импеданса. Обычно она встречается только в композитном фильтре .

Топологии мостовой Т-схемы

Фильтры постоянного сопротивления Цобеля ^[3] используют топологию, которая несколько отличается от других типов фильтров, отличаясь постоянным входным сопротивлением на всех частотах и тем, что они используют резистивные компоненты в конструкции своих секций. Большее количество компонентов и секций этих конструкций обычно ограничивает их применение приложениями эквализации. Топологии, обычно связанные с фильтрами постоянного сопротивления, — это мостовая Т-образная схема и ее варианты, все описанные в статье о сети Цобеля ;

Топология мостовой Т-образной структуры
Сбалансированная мостовая топология T
Топология L-образного сечения с разомкнутой цепью
Топология короткозамкнутой L-образной секции
Сбалансированная топология разомкнутой цепи С-образного сечения
Сбалансированная топология короткого замыкания С-образного сечения

Топология мостовой Т-схемы также используется в секциях, предназначенных для создания задержки сигнала, но в этом случае в конструкции не используются резистивные компоненты.

Решетчатая топология

Как T-секция (из топологии лестницы), так и мост-T (из топологии Цобеля) могут быть преобразованы в секцию фильтра решетчатой топологии, но в обоих случаях это приводит к большому количеству компонентов и сложности. Наиболее распространенное применение решетчатых фильтров (X-секций) — это всепроходные фильтры, используемые для выравнивания фаз . ^[4]

Хотя Т-образные и мостовые Т-образные секции всегда можно преобразовать в Х-образные секции, обратное преобразование не всегда возможно из-за возможности возникновения отрицательных значений индуктивности и емкости при преобразовании.

Решетчатая топология идентична более привычной мостовой топологии , разница заключается лишь в нарисованном на странице изображении, а не в какой-либо реальной разнице в топологии, схеме или функции.

Активные топологии

Топология множественной обратной связи

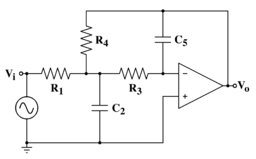
Топология с множественной обратной связью — это топология электронного фильтра, которая используется для реализации электронного фильтра путем добавления двух полюсов к передаточной функции . Схема топологии цепи для фильтра нижних частот второго порядка показана на рисунке справа.

Передаточная функция схемы с множественной топологией обратной связи, как и у всех линейных фильтров второго порядка , имеет вид:

H(s)={\frac {V_{o}}{V_{i}}}=-{\frac {1}{As^{2}+Bs+C}}={\frac {K{\omega _{0}}^{2}}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}

В фильтре MF,

A=(R_{1}R_{3}C_{2}C_{5})\,

B=R_{3}C_{5}+R_{1}C_{5}+R_{1}R_{3}C_{5}/R_{4}\,

C=R_{1}/R_{4}\,

Q={\frac {\sqrt {R_{3}R_{4}C_{2}C_{5}}}{(R_{4}+R_{3}+|K|R_{3})C_{5}}}

это Q-фактор .

K=-R_{4}/R_{1}\,

коэффициент усиления постоянного напряжения

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

это угловая частота

Для поиска подходящих значений компонентов для достижения желаемых свойств фильтра можно использовать подход, аналогичный подходу, описанному в разделе «Выбор конструкции» альтернативной топологии Саллена–Ки.

Топология биквадратного фильтра

Для цифровой реализации биквадратного фильтра см. раздел Цифровой биквадратный фильтр .

Биквадратный фильтр — это тип линейного фильтра , реализующего передаточную функцию , которая является отношением двух квадратичных функций . Название биквадрат является сокращением от биквадратный . Любая топология фильтра второго порядка может называться биквадратной , например, MFB или Sallen-Key. ^[5]^[6] Однако существует также особая топология «биквадрат». Иногда ее также называют схемой «кольцо из 3». ^{[ требуется цитата ]}

Биквадратные фильтры обычно активны и реализованы по топологии с одним усилителем-биквадом (SAB) или двумя интеграторными контурами .

Топология SAB использует обратную связь для генерации комплексных полюсов и, возможно, комплексных нулей . В частности, обратная связь перемещает действительные полюса RC-цепи для генерации надлежащих характеристик фильтра.
Топология двухинтеграторной петли получается путем перестановки биквадратной передаточной функции. Перестановка приравняет один сигнал к сумме другого сигнала, его интеграла и интеграла интеграла. Другими словами, перестановка выявляет структуру фильтра переменной состояния . Используя различные состояния в качестве выходов, можно реализовать любой тип фильтра второго порядка.

Топология SAB чувствительна к выбору компонентов и может быть более сложной в настройке. Поэтому обычно термин биквад относится к топологии фильтра переменной состояния с двумя интеграторами и контурами.

Фильтр Tow-Thomas

Рисунок 1. Распространенная топология биквадратного фильтра Тоу-Томаса.

Например, базовая конфигурация на рисунке 1 может использоваться как фильтр нижних частот или полосовой фильтр в зависимости от того, откуда берется выходной сигнал.

Передаточная функция нижних частот второго порядка определяется выражением

H(s)={\frac {G_{\mathrm {lpf} }{\omega _{0}}^{2}}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}

где коэффициент усиления нижних частот . Передаточная функция полосы пропускания второго порядка определяется выражением $G_{\mathrm {lpf} }=-R_{2}/R_{1}$

H(s)={\frac {G_{\mathrm {bpf} }{\frac {\omega _{0}}{Q}}s}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}

с усилением полосы пропускания . В обоих случаях $G_{\mathrm {bpf} }=-R_{3}/R_{1}$

Собственная частота составляет . $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$
Коэффициент качества равен . $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$

Полоса пропускания аппроксимируется как , а Q иногда выражается как константа затухания . Если требуется неинвертирующий фильтр нижних частот, выходной сигнал может быть взят на выходе второго операционного усилителя , после переключения порядка второго интегратора и инвертора. Если требуется неинвертирующий полосовой фильтр, порядок второго интегратора и инвертора может быть переключен, а выходной сигнал взят на выходе операционного усилителя инвертора. $B=\omega _{0}/Q$ $\дзета =1/2Q$

Фильтр Акерберга-Моссберга

На рисунке 2 показан вариант топологии Тоу-Томаса, известный как топология Акерберга-Моссберга, в которой используется активно компенсированный интегратор Миллера, что улучшает характеристики фильтра.

Топология Саллена–Ки

Конструкция Саллена-Ки представляет собой неинвертирующий фильтр второго порядка с возможностью высокой добротности и усиления в полосе пропускания.

Смотрите также

Примечания

^ Зобель, 1923
^ Для этого типа фильтров не существует общепризнанного названия: Цобель (1923, стр. 11) использовал название Общие волновые фильтры, имеющие любые предварительно заданные полосы пропускания и ослабления и постоянные распространения, регулируемые без изменения одного характеристического импеданса средней точки . Поскольку Цобель называет параметры m ₁ , m ₂ и т. д., сокращение общий m _n -тип кажется разумным для использования здесь.
^ Зобель, 1928
^ Зобель, 1931
^ "A Beginner's Guide to Filter Topologies". Maxim Integrated . Архивировано из оригинала 2019-10-28 . Получено 2021-07-30 . Это означает, что фильтры Саллена-Ки, переменные фильтры состояния, фильтры с множественной обратной связью и другие типы являются биквадами. Также есть топология "биквад", которая помогает еще больше запутать вещи.
^ Мошиц, Джордж С. (2019). Аналоговая теория цепей и проектирование фильтров в цифровом мире: с введением в морфологический метод для творческих решений и проектирования. Хам, Швейцария. ISBN 978-3-030-00096-7OCLC 1100066185. множество схем активных фильтров второго порядка с одним усилителем… числитель и знаменатель которых имеют второй порядок, т . е. являются биквадратными; поэтому их называют «биквадратами»{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

Ссылки

Кэмпбелл, GA, «Физическая теория электрического волнового фильтра», Bell System Technical Journal , ноябрь 1922 г., т. 1, № 2, стр. 1–32.
Зобель, О. Дж., «Теория и проектирование однородных и составных электрических волновых фильтров», Bell System Technical Journal , т. 2 (1923).
Фостер, Р. М., «Теорема о реактивном сопротивлении», Bell System Technical Journal , т. 3 , стр. 259–267, 1924.
Кауэр, В., «Die Verwirklichung der Wechselstromwiderstande vorgeschriebener Frequenzabhängigkeit», Archiv für Elektrotechnik , 17 , стр. 355–388, 1926.
Зобель, О. Дж., «Коррекция искажений в электрических сетях с рекуррентными сетями постоянного сопротивления», Bell System Technical Journal , том 7 (1928), стр. 438.
Зобель, О. Дж., Фазосдвигающая сеть , патент США 1 792 523, подан 12 марта 1927 г., выдан 17 февраля 1931 г.

Внешние ссылки

Медиафайлы по теме «Топология электронного фильтра» на Wikimedia Commons