Барьер деления

Энергия активации, необходимая для деления ядра атома

Индуцированная реакция деления . Ядро возбуждается некоторым ядерным процессом, а затем расщепляется на более легкие элементы ( продукты деления ). Это высвобождает небольшое количество нейтронов и мгновенное гамма-излучение , за которым следует бета-распад более легких ядер с выделением дополнительного гамма-излучения. ^[1]

В ядерной физике и ядерной химии барьер деления — это энергия активации, необходимая для того, чтобы ядро ​​атома подверглось делению . Этот барьер также можно определить как минимальное количество энергии, необходимое для деформации ядра до точки, в которой оно безвозвратно предано процессу деления. Энергия для преодоления этого барьера может поступать либо от нейтронной бомбардировки ядра, когда дополнительная энергия от нейтрона приводит ядро ​​в возбужденное состояние и подвергается деформации, либо через спонтанное деление , когда ядро ​​уже находится в возбужденном и деформированном состоянии.

Важно отметить, что попытки понять процессы деления все еще продолжаются и представляют собой очень сложную задачу с тех пор, как деление было впервые обнаружено Лизой Мейтнер , Отто Ганом и Фрицем Штрассманом в 1938 году. ^[2] Хотя физики-ядерщики понимают многие аспекты процесса деления, в настоящее время не существует всеобъемлющей теоретической структуры, которая давала бы удовлетворительное описание основных наблюдений.

Раскол

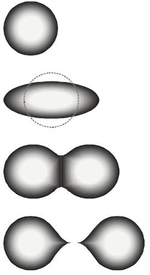
Процесс деления можно понять, когда ядро ​​с некоторой равновесной деформацией поглощает энергию (например, через захват нейтронов ), становится возбужденным и деформируется в конфигурацию, известную как конфигурация «переходного состояния» или «седловой точки». По мере деформации ядра ядерная кулоновская энергия уменьшается, а ядерная поверхностная энергия увеличивается. В седловой точке скорость изменения кулоновской энергии равна скорости изменения ядерной поверхностной энергии. Образование и возможный распад этого переходного состояния ядра является определяющим скорость шагом в процессе деления и соответствует прохождению через барьер энергии активации к реакции деления. Когда это происходит, шейка между зарождающимися фрагментами исчезает, и ядро ​​делится на два фрагмента. Точка, в которой это происходит, называется «точкой разрыва». ^[3]

Модель капли жидкости

Из описания начала процесса деления до «точки разрыва» очевидно, что изменение формы ядра связано с изменением энергии некоторого рода. Фактически, это изменение двух типов энергии: (1) макроскопической энергии, связанной с ядерными объемными свойствами, как задано моделью жидкой капли , и (2) квантово-механической энергии, связанной с заполнением орбиталей оболочечной модели. ^[4] Для ядерных объемных свойств с малыми искажениями поверхностная, , и кулоновская, , энергии определяются следующим образом: ${\displaystyle E_{s}}$ ${\displaystyle E_{c}}$

${\displaystyle E_{s}=E_{s}^{0}\left(1+{\frac {2}{5}}\alpha _{2}^{2}\right)}$

${\displaystyle E_{c}=E_{c}^{0}\left(1-{\frac {1}{5}}\alpha _{2}^{2}\right)}$

где и — поверхностная и кулоновская энергии неискаженных сферических капель, соответственно, а — параметр квадрупольного искажения. Когда изменения кулоновской и поверхностной энергий ( , ) равны, ядро ​​становится нестабильным относительно деления. В этой точке соотношение между неискаженной поверхностной и кулоновской энергиями становится: ${\displaystyle E_{s}^{0}}$ ${\displaystyle E_{c}^{0}}$ ${\displaystyle \alpha _{2}}$ ${\displaystyle \Delta E_{c}=E_{c}^{0}-E_{c}}$ ${\displaystyle \Delta E_{s}=E_{s}^{0}-E_{s}}$

${\displaystyle x={\frac {E_{c}^{0}}{2E_{s}^{0}}}}$

где называется параметром делимости. Если , то энергия жидкой капли уменьшается с ростом , что приводит к делению. Если , то энергия жидкой капли уменьшается с уменьшением , что приводит к сферическим формам ядра. ${\displaystyle x}$ ${\displaystyle x>1}$ ${\displaystyle \alpha _{2}}$ ${\displaystyle x<1}$ ${\displaystyle \alpha _{2}}$

Кулоновскую и поверхностную энергии равномерно заряженной сферы можно аппроксимировать следующими выражениями:

${\displaystyle E_{c}^{0}={\frac {3}{5}}{\frac {Z^{2}e^{2}}{R_{0}A^{1/3}}}=a_{c}{\frac {Z^{2}}{A^{1/3}}}}$

${\displaystyle E_{s}^{0}=4\pi R_{0}^{2}SA^{2/3}=a_{s}A^{2/3}}$

где — атомный номер ядра, — массовое число ядра, — заряд электрона, — радиус недеформированного сферического ядра, — поверхностное натяжение на единицу площади ядра, и . Уравнение для параметра делимости тогда принимает вид: ${\displaystyle Z}$ ${\displaystyle A}$ ${\displaystyle e}$ ${\displaystyle R_{0}}$ ${\displaystyle S}$ ${\displaystyle a_{c}=3e^{2}/5R_{0}}$ ${\displaystyle a_{s}=4\pi R_{0}^{2}S}$

${\displaystyle x=\left({\frac {a_{c}}{2a_{s}}}\right)\left({\frac {Z^{2}}{A}}\right)=\left({\frac {Z^{2}}{A}}\right)/\left({\frac {Z^{2}}{A}}\right)_{critical}}$

где отношение константы обозначается как . Делимость данного ядра может быть затем классифицирована относительно . Например, плутоний-239 имеет значение 36,97, в то время как менее делящиеся ядра, такие как висмут-209, имеют значение 32,96. ${\displaystyle \left(a_{c}/2a_{s}\right)^{-1}}$ ${\displaystyle \left(Z^{2}/A\right)_{critical}}$ ${\displaystyle \left(Z^{2}/A\right)}$ ${\displaystyle \left(Z^{2}/A\right)}$ ${\displaystyle \left(Z^{2}/A\right)}$

Для всех стабильных ядер должно быть меньше 1. В этом случае полная энергия деформации ядер, подвергающихся делению, увеличится на величину , поскольку ядро ​​деформируется в сторону деления. Это увеличение потенциальной энергии можно рассматривать как барьер энергии активации для реакции деления. Однако современные расчеты потенциальной энергии деформации для модели жидкой капли включают в себя множество координат деформации помимо и представляют собой основные вычислительные задачи. ${\displaystyle x}$ ${\displaystyle (1/5)\alpha _{2}^{2}(2E_{s}^{0}-E_{c}^{0})}$ ${\displaystyle \alpha _{2}}$

Поправки к оболочке

Для того чтобы получить более разумные значения для ядерных масс в модели жидкой капли, необходимо включить оболочечные эффекты. Советский физик Вилен Струтинский предложил такой метод, используя «оболочечную поправку» и поправки на спаривание ядер в модели жидкой капли. ^[5] В этом методе полная энергия ядра берется как сумма энергии модели жидкой капли, , оболочечной , , и спаривания, , поправок к этой энергии как: ${\displaystyle E_{LDM}}$ ${\displaystyle \delta S}$ ${\displaystyle \delta P}$

${\displaystyle E=E_{LDM}+\sum _{p,n}(\delta S+\delta P)}$

Оболочечные поправки, как и энергия жидкой капли, являются функциями ядерной деформации. Оболочечные поправки имеют тенденцию понижать массы основного состояния сферических ядер с магическими или почти магическими числами нейтронов и протонов . Они также имеют тенденцию понижать массу основного состояния ядер средней оболочки при некоторой конечной деформации, таким образом объясняя деформированную природу актинидов . Без этих оболочечных эффектов самые тяжелые ядра не могли бы наблюдаться, поскольку они распадались бы путем спонтанного деления в масштабе времени, намного более коротком, чем мы можем наблюдать.

Это сочетание макроскопических эффектов жидкой капли и микроскопических оболочек предсказывает, что для ядер в области U - Pu возникнет двугорбый барьер деления с равными высотами барьеров и глубоким вторичным минимумом. Для более тяжелых ядер, таких как калифорний , первый барьер, как предсказывают, будет намного больше второго барьера, и прохождение через первый барьер является определяющим скорость. В целом, существует достаточно экспериментальных и теоретических доказательств того, что путь с наименьшей энергией в процессе деления соответствует тому, что ядро, изначально в аксиально-симметричной и симметричной по массе (отражение) форме, проходит через первый максимум в барьере деления с аксиально-асимметричной, но симметричной по массе формой, а затем проходит через второй максимум в барьере с аксиально-симметричной, но асимметричной по массе (отражение) формой. Из-за сложного многомерного характера процесса деления не существует простых формул для высот барьера деления. Однако существуют обширные таблицы экспериментальных характеристик высот барьеров деления для различных ядер. ^{[4] [6]}

Смотрите также

• Портал ядерных технологий
• Энергетический портал

• Холодное деление
• Ядерный синтез

Ссылки

1. Л. Яффе (1968). «Деление ядра». Ядерная химия . Т. II. Нью-Йорк: Academic Press. ASIN  B0066F5SQE.
2. HG Graetzer (1964). «Открытие деления ядра». American Journal of Physics . 32 (1): 9–15. Bibcode :1964AmJPh..32....9G. doi : 10.1119/1.1970127 .
3. BD Wilkins; EP Steinberg & RR Chasman (1976). "Модель точки разрыва ядерного деления на основе эффектов деформированной оболочки". Physical Review C. 14 ( 5): 1832–1863. Bibcode : 1976PhRvC..14.1832W. doi : 10.1103/PhysRevC.14.1832.
4. R. Vandenbosch & JR Huizenga (1974). Ядерное деление . Нью-Йорк: Academic Press. ASIN  B012YSETDY.
5. В. М. Струтинский (1967). «Оболочечные эффекты в ядерных массах и энергиях деформации». Nuclear Physics A. 95 ( 2): 420–442. Bibcode :1967NuPhA..95..420S. doi :10.1016/0375-9474(67)90510-6. ISSN  0375-9474.
6. К. Вейджманс (1991). Процесс ядерного деления . Бока-Ратон: CRC Press. ISBN 9780849354342.