Бесплатная группа

Математическая концепция

Диаграмма, показывающая граф Кэли для свободной группы на двух генераторах. Каждая вершина представляет элемент свободной группы, а каждое ребро представляет умножение на a или b .

В математике свободная группа F _S над заданным множеством S состоит из всех слов , которые можно построить из элементов S , считая два слова различными, если их равенство не следует из аксиом группы (например, st = suu ⁻¹ t , но s ≠ t ⁻¹ для s , t , u ∈ S ). Элементы S называются генераторами F _S , а число генераторов — рангом свободной группы. Произвольная группа G называется свободной , если она изоморфна F _S для некоторого подмножества S множества G , то есть если существует подмножество S множества G такое, что каждый элемент G может быть записан ровно одним способом как произведение конечного числа элементов S и их обратных (без учета тривиальных вариаций, таких как st = suu ⁻¹ t ).

Связанное, но другое понятие — свободная абелева группа ; оба понятия являются частными случаями свободного объекта из универсальной алгебры . Таким образом, свободные группы определяются своим универсальным свойством.

История

Свободные группы впервые возникли при изучении гиперболической геометрии как примеры фуксовых групп (дискретных групп, действующих посредством изометрий на гиперболической плоскости ). В статье 1882 года Вальтер фон Дейк указал, что эти группы имеют простейшие возможные представления . ^[1] Алгебраическое изучение свободных групп было инициировано Якобом Нильсеном в 1924 году, который дал им их название и установил многие из их основных свойств. ^{[2] [3] [4]} Макс Ден осознал связь с топологией и получил первое доказательство полной теоремы Нильсена–Шрайера . ^[5] Отто Шрайер опубликовал алгебраическое доказательство этого результата в 1927 году, ^[6] а Курт Рейдемейстер включил всестороннее рассмотрение свободных групп в свою книгу 1932 года по комбинаторной топологии . ^[7] Позднее, в 1930-х годах, Вильгельм Магнус открыл связь между нижним центральным рядом свободных групп и свободными алгебрами Ли .

Примеры

Группа ( Z ,+) целых чисел свободна от ранга 1; порождающее множество — S = {1}. Целые числа также являются свободной абелевой группой , хотя все свободные группы ранга неабелевы. Свободная группа на двухэлементном множестве S встречается в доказательстве парадокса Банаха–Тарского и там описана. ${\displaystyle \geq 2}$

С другой стороны, любая нетривиальная конечная группа не может быть свободной, поскольку элементы свободного порождающего множества свободной группы имеют бесконечный порядок.

В алгебраической топологии фундаментальная группа букета из k окружностей (набора из k контуров, имеющих только одну общую точку) — это свободная группа на наборе из k элементов.

Строительство

Свободная группа F _S со свободным порождающим множеством S может быть построена следующим образом. S — это множество символов, и мы предполагаем, что для каждого s в S существует соответствующий «обратный» символ, s ⁻¹ , в множестве S ⁻¹ . Пусть T  =  S  ∪  S ⁻¹ , и определим слово в S как любое записанное произведение элементов T . То есть, слово в S является элементом моноида , порожденного T . Пустое слово — это слово без каких-либо символов вообще. Например, если S  = ​​{ a ,  b ,  c }, то T  = { a ,  a ⁻¹ ,  b ,  b ⁻¹ ,  c ,  c ⁻¹ }, и

${\displaystyle ab^{3}c^{-1}ca^{-1}c\,}$

это слово на языке S.

Если элемент S находится непосредственно рядом с его обратным элементом, слово можно упростить, опустив пару c, c ⁻¹ :

${\displaystyle ab^{3}c^{-1}ca^{-1}c\;\;\longrightarrow \;\;ab^{3}\,a^{-1}c.}$

Слово, которое невозможно упростить еще больше, называется сокращенным .

Свободная группа F _S определяется как группа всех редуцированных слов в S , с конкатенацией слов (с последующей редукцией, если необходимо) в качестве групповой операции. Идентичностью является пустое слово.

Сокращённое слово называется циклически сокращённым , если его первая и последняя буквы не являются обратными друг другу. Каждое слово сопряжено с циклически сокращённым словом, а циклически сокращённое сопряжённое циклически сокращённого слова является циклической перестановкой букв в слове. Например, b ⁻¹ abcb не является циклически сокращённым, но сопряжён с abc , которое циклически сокращённо. Единственными циклически сокращёнными сопряжёнными abc являются abc , bca и cab .

Универсальная собственность

Свободная группа F _S является универсальной группой, порожденной множеством S. Это можно формализовать следующим универсальным свойством : для любой функции f из S в группу G существует единственный гомоморфизм φ :  F _S  →  G, делающий следующую диаграмму коммутативной (где неназванное отображение обозначает включение из S в F _S ):

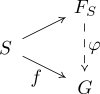
То есть гомоморфизмы F _S  →  G находятся во взаимно однозначном соответствии с функциями S  →  G. Для несвободной группы наличие соотношений ограничило бы возможные образы генераторов при гомоморфизме.

Чтобы увидеть, как это соотносится с конструктивным определением, представьте себе отображение из S в F _S как отправку каждого символа в слово, состоящее из этого символа. Чтобы построить φ для заданного f , сначала заметим, что φ отправляет пустое слово в единицу G , и оно должно согласовываться с f на элементах S . Для оставшихся слов (состоящих более чем из одного символа) φ может быть однозначно расширено, поскольку это гомоморфизм, т. е. φ ( ab ) = φ ( a ) φ ( b ).

Вышеуказанное свойство характеризует свободные группы с точностью до изоморфизма и иногда используется как альтернативное определение. Оно известно как универсальное свойство свободных групп, а порождающее множество S называется базисом для F _S . Базис для свободной группы не определен однозначно.

Характеризуемость универсальным свойством является стандартной чертой свободных объектов в универсальной алгебре . На языке теории категорий конструкция свободной группы (подобная большинству конструкций свободных объектов) является функтором из категории множеств в категорию групп . Этот функтор является левым сопряженным к забывающему функтору из групп в множества.

Факты и теоремы

Некоторые свойства свободных групп легко следуют из определения:

1. Любая группа G является гомоморфным образом некоторой свободной группы F _S . Пусть S — множество порождающих групп G . Естественное отображение φ : F _S → G является эпиморфизмом , что доказывает утверждение. Эквивалентно, G изоморфна фактор-группе некоторой свободной группы F S . Если S можно выбрать здесь конечной, то G называется конечно порожденной . Ядро Ker( φ) — это множество всех отношений в представлении G ; если Ker( φ) может быть порождено сопряженными элементами конечного числа групп _F , то G конечно порождена.
2. Если S имеет более одного элемента, то F S не является абелевым, и фактически центр F S _{тривиален} ( то есть состоит только _из единичного элемента).
3. Две свободные группы F _S и F _T изоморфны тогда и только тогда, когда S и T имеют одинаковую мощность . Эта мощность называется рангом свободной группы F . Таким образом, для каждого кардинального числа k , с точностью до изоморфизма существует ровно одна свободная группа ранга k .
4. Свободная группа конечного ранга n > 1 имеет экспоненциальную скорость роста порядка 2 n − 1.

Вот еще несколько связанных результатов:

1. Теорема Нильсена –Шрайера : Каждая подгруппа свободной группы свободна. Более того, если свободная группа F имеет ранг n , а подгруппа H имеет индекс e в F , то H свободна ранга 1 + e ( n– 1).
2. Свободная группа ранга k, очевидно, имеет подгруппы любого ранга, меньшего k . Менее очевидно, что ( неабелева! ) свободная группа ранга не менее 2 имеет подгруппы всех счетных рангов.
3. Коммутант свободной группы ранга k > 1 имеет бесконечный ранг; например, для F( ^a , b ) он свободно порождается коммутаторами [ am , bn ] ^для ненулевых m и n .
4. Свободная группа из двух элементов является SQ универсальной ; вышеизложенное следует из того, что любая SQ универсальная группа имеет подгруппы всех счетных рангов.
5. Любая группа, действующая на дереве свободно и сохраняющая ориентацию , является свободной группой счетного ранга (задаваемого 1 плюс эйлерова характеристика факторграфа ).
6. Граф Кэли свободной группы конечного ранга относительно свободного порождающего множества — это дерево , на котором группа действует свободно, сохраняя ориентацию. Как топологическое пространство (одномерный симплициальный комплекс ), этот граф Кэли Γ( F ) является стягиваемым . Для конечно представленной группы G естественный гомоморфизм, определенный выше, φ  : F → G , определяет накрывающее отображение графов Кэли φ*  : Γ( F ) → Γ( G ), фактически универсальное накрытие. Следовательно, фундаментальная группа графа Кэли Γ( G ) изоморфна ядру φ , нормальной подгруппе соотношений между порождающими элементами G . Крайний случай — когда G = { e }, тривиальная группа, рассматриваемая с таким же количеством порождающих элементов, как F , все из которых тривиальны; Граф Кэли Γ( G ) представляет собой букет окружностей, а его фундаментальная группа — это сама F.
7. Любая подгруппа свободной группы, , соответствует покрывающему пространству букета окружностей, а именно графу смежных классов Шрайера F / H. Это можно использовать для топологического доказательства теоремы Нильсена-Шрайера выше. ${\displaystyle H\subset F}$
8. Группоидный подход к этим результатам, представленный в работе П. Дж . Хиггинса ниже, связан с использованием покрывающих пространств выше. Он позволяет получить более мощные результаты, например, по теореме Грушко , и нормальную форму для фундаментального группоида графа групп. В этом подходе значительно используются свободные группоиды на ориентированном графе.
9. Теорема Грушко имеет следствие, что если подмножество B свободной группы F на n элементах порождает F и имеет n элементов, то B порождает F свободно.

Свободная абелева группа

Свободная абелева группа на множестве S определяется через ее универсальное свойство аналогичным образом с очевидными изменениями: рассмотрим пару ( F , φ ), где F — абелева группа, а φ : S → F — функция. F называется свободной абелевой группой на S относительно φ, если для любой абелевой группы G и любой функции ψ : S → G существует единственный гомоморфизм f : F → G такой, что

f ( φ ( s )) = ψ ( s ), для всех s из S .

Свободная абелева группа на S может быть явно идентифицирована как свободная группа F( S ) по модулю подгруппы, порожденной ее коммутаторами, [F( S ), F( S )], т.е. ее абелианизация . Другими словами, свободная абелева группа на S — это множество слов, которые различаются только с точностью до порядка букв. Поэтому ранг свободной группы может быть также определен как ранг ее абелианизации как свободной абелевой группы.

Проблемы Тарского

Около 1945 года Альфред Тарский задался вопросом, имеют ли свободные группы с двумя или более генераторами одну и ту же теорию первого порядка , и разрешима ли эта теория . Села (2006) ответил на первый вопрос, показав, что любые две неабелевы свободные группы имеют одну и ту же теорию первого порядка, а Харлампович и Мясников (2006) ответили на оба вопроса, показав, что эта теория разрешима.

Похожий нерешенный (по состоянию на 2011 год) вопрос в теории свободных вероятностей заключается в том, являются ли групповые алгебры фон Неймана любых двух неабелевых конечно порожденных свободных групп изоморфными.

Смотрите также

• Генерация набора группы
• Представление группы
• Преобразование Нильсена , факторизация элементов группы автоморфизмов свободной группы
• Нормальная форма для свободных групп и свободного произведения групп
• Бесплатный продукт

Примечания

1. фон Дейк, Вальтер (1882). «Gruppentheoretische Studien (Теоретико-групповые исследования)». Математические Аннален . 20 (1): 1–44. дои : 10.1007/BF01443322. S2CID  179178038. Архивировано из оригинала 04 марта 2016 г. Проверено 1 сентября 2015 г.
2. Нильсен, Якоб (1917). «Die Isomorphismen der allgemeinen unendlichen Gruppe mit zwei Erzeugenden». Математические Аннален . 78 (1): 385–397. дои : 10.1007/BF01457113. ЖФМ  46.0175.01. MR  1511907. S2CID  119726936. Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.
3. Нильсен, Якоб (1921). «О вычислении с некоммутативными множителями и его применении к теории групп. (Перевод с датского)». The Mathematical Scientist . 6 (1981) (2): 73–85.
4. Нильсен, Якоб (1924). «Die Isomorphismengruppe der Freien Gruppen». Математические Аннален . 91 (3): 169–209. дои : 10.1007/BF01556078. S2CID  122577302. Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.
5. См. Магнус, Вильгельм ; Муфанг, Рут (1954). «Макс Ден цум Гедехтнис». Математические Аннален . 127 (1): 215–227. дои : 10.1007/BF01361121. S2CID  119917209. Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.
6. Шрайер, Отто (1928). «Die Untergruppen der Freien Gruppen». Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg . 5 : 161–183. дои : 10.1007/BF02952517. S2CID  121888949.
7. Рейдемейстер, Курт (1972) [1932]. Einführung in die kombinatorische Topologie . Дармштадт: Wissenschaftliche Buchgesellschaft.

Ссылки

• Харлампович, Ольга; Мясников, Алексей (2006). «Элементарная теория свободных неабелевых групп». Журнал алгебры . 302 (2): 451–552. doi : 10.1016/j.jalgebra.2006.03.033 . MR  2293770.
• В. Магнус, А. Каррасс и Д. Солитэр, «Комбинаторная теория групп», Довер (1976).
• PJ Higgins, 1971, «Категории и группоиды», van Nostrand, {Нью-Йорк}. Переиздание в Theory and Applications of Categories, 7 (2005) стр. 1–195.
• Sela, Zlil (2006). «Диофантова геометрия над группами. VI. Элементарная теория свободной группы». Geom. Funct. Anal . 16 (3): 707–730. doi :10.1007/s00039-006-0565-8. MR  2238945. S2CID  123197664.
• Серр, Жан-Пьер , Деревья , Спрингер (2003) (английский перевод «arbres, amalgames, SL ₂ », 3-е издание, звездочка 46 (1983))
• П. Дж. Хиггинс, Фундаментальный группоид графа групп , Журнал Лондонского математического общества (2) 13 (1976), № 1, 145–149.
• Алуффи, Паоло (2009). Алгебра: Глава 0. AMS Bookstore. стр. 70. ISBN 978-0-8218-4781-7..
• Грилье, Пьер Антуан (2007). Абстрактная алгебра. Спрингер. п. 27. ISBN 978-0-387-71567-4..