Пифагорейские молоты

Гаффуриус , Theorica musicae (1492): Пифагор, исследующий гармонию и соотношение с различными музыкальными инструментами.

Согласно легенде, Пифагор открыл основы музыкальной настройки , слушая звуки четырех кузнечных молотов, которые производили консонанс и диссонанс при одновременном ударе. Согласно Никомаху в его «Энхиридионе гармоник » II в. н. э . ^[1] Пифагор заметил, что молоток A производил консонанс с молотком B, когда их ударяли вместе, а молоток C производил консонанс с молотком A, но молотки B и C производили диссонанс друг с другом. Молоток D производил такой совершенный консонанс с молотком A, что они, казалось, «пели» одну и ту же ноту. Пифагор бросился в кузницу, чтобы выяснить, почему, и обнаружил, что объяснение было в соотношении веса. Молотки весили 12, 9, 8 и 6 фунтов соответственно. Молотки A и D находились в соотношении 2:1, что является соотношением октавы . Молотки B и C весили 8 и 9 фунтов. Их соотношения с молоточком D были (12:8 = 3:2 = чистая квинта ) и (12:9 = 4:3 = чистая кварта ). Пространство между B и C составляет соотношение 9:8, что равно музыкальному целому тону , или интервалу целого шага ( Игра 9/8 ^ⓘ ).

Легенда, по крайней мере в отношении молоточков, явно ложна. Вероятно, это ближневосточная народная сказка. ^[2] Эти пропорции действительно имеют отношение к длине струны (например, монохорда ) — используя эти базовые интервалы, можно построить хроматическую гамму и базовую семитональную диатоническую гамму, используемую в современной музыке, и Пифагор, возможно, оказал влияние на открытие этих пропорций (поэтому иногда их называют пифагорейской настройкой ) — но пропорции не имеют того же отношения к весу молоточков и тонам, производимым ими. ^{[3] [4] Однако,} долота с равным поперечным сечением, приводимые в движение молоточковым механизмом , показывают точную пропорцию между длиной или весом и собственной частотой . ^[5]

Более ранние источники упоминают интерес Пифагора к гармонии и соотношению. Ксенократ (IV в. до н. э.), хотя, насколько нам известно, не упоминал историю о кузнеце, описал интерес Пифагора в общих чертах: «Пифагор также открыл, что интервалы в музыке не возникают отдельно от числа; ибо они являются взаимосвязью количества с количеством. Поэтому он отправился исследовать, при каких условиях возникают согласные интервалы и несогласные интервалы, и все хорошо и плохо настроенное». ^[6] Каковы бы ни были подробности открытия связи между музыкой и соотношением, оно рассматривается ^{[7] как исторически первое эмпирически надежное математическое описание физического факта. Как таковое, оно символизирует и, возможно, ведет к пифагорейской концепции математики как} modus operandi природы . ^[8] Как позже напишет Аристотель , « пифагорейцы создают всю вселенную из чисел». ^[9] Микролог Гвидо из Ареццо повторяет легенду в главе XX. ^[10]

• 
  Размеры четырех пифагорейских молотов.

Содержание легенды

Согласно самой старой записанной версии ^[11] легенды, Пифагор, живший в VI веке до н. э., искал инструмент для измерения акустических восприятий, подобно тому, как геометрические величины измеряются циркулем или веса с помощью весов. Когда он проходил мимо кузницы, где четыре (согласно более поздней версии, пять) мастеров работали молотами, он заметил, что каждый удар производил тоны разной высоты , что приводило к гармонии при парном сочетании. Он мог различать октаву , квинту и кварту . Только одну пару, которая образовывала интервал между квартой и квинтой (большая секунда ), он воспринимал как диссонансную . Взволнованный, он побежал в кузницу, чтобы провести эксперименты. Там он обнаружил, что разница в высоте тона не зависела от формы молотка, положения ударяемого железа или силы удара. Скорее, он мог связать высоту тона с весом молотков, который он точно измерил. Затем он вернулся домой, чтобы продолжить эксперименты.

Он повесил четыре одинаково длинные, одинаково прочные и одинаково скрученные струны последовательно на колышек, прикрепленный по диагонали к углу стен, утяжелив их по-разному, прикрепив разные грузики внизу. Затем он ударил по струнам попарно, и зазвучали те же гармонии, что и в кузнице. Струна с самой тяжелой нагрузкой в ​​двенадцать единиц, будучи соединенной с наименее нагруженной струной, несущей шесть единиц, производила октаву. Таким образом, было очевидно, что октава была основана на соотношении 12:6 или 2:1. Самая натянутая струна дала квинту со второй самой свободной струной (восемь единиц), и кварту со второй самой натянутой струной (девять единиц). Из этого следовало, что квинта была основана на соотношении 12:8 или 3:2, а четвертая — на соотношении 12:9 или 4:3. Опять же, отношение второй самой тугой струны к самой свободной, 9:6 или 3:2, дало квинту, а отношение второй самой свободной к самой свободной, 8:6 или 4:3, дало кварту. Для диссонансного интервала между квинтой и квартой было обнаружено, что он основан на соотношении 9:8, что совпало с измерениями веса, проведенными в кузнице. Октава оказалась произведением квинты и кварты:

${\displaystyle {\frac {3}{2}}\cdot {\frac {4}{3}}={\frac {12}{6}}={\frac {2}{1}}=2}$

Затем Пифагор распространил эксперимент на различные инструменты, экспериментировал с сосудами, флейтами, треугольниками , монохордом и т. д., всегда находя те же числовые соотношения. Наконец, он ввел общепринятую терминологию для относительной высоты звука.

Дальнейшие традиции

С изобретением монохорда для исследования и демонстрации гармоний пар струн с различными целочисленными отношениями длины Пифагор, как говорят, ввел удобное средство иллюстрации математической основы теории музыки, которую он открыл. Монохорд, называемый κανών (kanōn) по-гречески и regula по-латыни, представляет собой резонирующий ящик с натянутой на него струной. К ящику прикреплена измерительная шкала. Устройство оснащено подвижным мостиком, который позволяет делить вибрирующую длину струны; деление можно точно определить с помощью измерительной шкалы. Это позволяет измерять интервалы. Несмотря на название «монохорд», что означает «однострунный», существовали также многострунные монохорды, которые могли производить одновременные интервалы. Однако неясно, когда был изобретен монохорд. Вальтер Буркерт датирует это достижение временем после эпохи Аристотеля , который, по-видимому, не знал этого устройства; Таким образом, он был введен спустя много времени после смерти Пифагора. ^[12] С другой стороны, Леонид Жмуд предполагает, что Пифагор, вероятно, проводил свой эксперимент, который привел к открытию числовых соотношений, используя монохорд. ^[13]

Гиппас из Метапонта , ранний пифагореец (конец VI и начало V вв. до н. э.), проводил количественные исследования музыкальных интервалов. Эксперимент, приписываемый Гиппасу, включающий свободно колеблющиеся круглые пластины различной толщины, является физически правильным, в отличие от предполагаемых экспериментов Пифагора. Неясно, проводил ли Архит из Тарента , важный пифагореец V/IV вв. до н. э., соответствующие эксперименты. Он, вероятно, был больше теоретиком, чем практиком в музыке, но он ссылался на акустические наблюдения своих предшественников. Музыкальные примеры, которые он приводит в поддержку своей акустической теории, включают духовые инструменты; он не упоминает эксперименты со струнными инструментами или отдельными струнами. Архит исходил из ошибочной гипотезы, что высота тона зависит от скорости распространения звука и силы удара по звукоиздающему телу; в действительности скорость звука постоянна в данной среде, а сила влияет только на громкость. ^[14]

Интерпретация легенды

Вальтер Буркерт считает, что, несмотря на свою физическую невозможность, легенду не следует рассматривать как произвольное изобретение, а скорее как имеющую смысл, который можно найти в греческой мифологии . Идейские дактили , мифические изобретатели кузнечного дела, были также, согласно мифу, изобретателями музыки. Таким образом, уже существовала очень древняя традиция, связывающая кузнечное дело с музыкой, в которой мифические кузнецы изображались как обладатели секрета магической музыки. Буркерт рассматривает легенду о Пифагоре в кузнецах как позднюю трансформацию и рационализацию древнего мифа о дактиле: В легенде о Пифагоре кузнецы больше не предстают как обладатели древних магических знаний, а скорее, не намереваясь этого делать, они становятся — хотя и не зная этого — «учителями» Пифагора. ^[15]

В раннем Средневековье Исидор Севильский называл библейского кузнеца Тубала изобретателем музыки; более поздние авторы последовали за ним в этом. Эта традиция еще раз показывает идею связи между кузнечным делом и музыкой, которая также появляется в неевропейских мифах и легендах. ^[16] Тубал был единокровным братом Иубала , который считался предком всех музыкантов. Оба были сыновьями Ламеха и, таким образом, внуками Каина . В некоторых христианских традициях Средневековья Иубал, который наблюдал за своим братом Тубалом, приравнивался к Пифагору. ^[17]

Другое объяснение предлагает Йорген Раастед, вслед за Леонидом Жмудом. Гипотеза Раастед утверждает, что отправной точкой формирования легенды был отчет об экспериментах Гиппаса. Гиппас использовал сосуды, называемые «sphaírai». Это слово было ошибочно спутано со «sphýrai» (молотками) из-за ошибки переписчика, и вместо имени Гиппаса было использовано имя Пифагора как создателя экспериментов. Отсюда и возникла легенда о кузнице. ^[18]

Основы теории музыки

Целые числа 6, 8, 9 и 12 по отношению к самому низкому тону (номер 12) соответствуют чистым интервалам кварта (номер 9), квинта (номер 8) и октава (номер 6) вверх:

Такие чистые интервалы воспринимаются человеческим ухом как без битов , так как громкость тонов не меняется. В нотах эти четыре пифагорейских тона могут быть выражены, например, мелодической последовательностью c' – f' – g' – c":

Если эту последовательность тонов рассматривать не с самого низкого, а с самого высокого тона (номер 6), то получатся также следующие интервалы: кварта (номер 8), квинта (номер 9) и октава (номер 12) — в данном случае, однако, по убыванию:

Квинта и октава появляются по отношению к основному тону в натуральных гармонических рядах, но не кварта или ее октавный эквивалент. Этот интервал кварты встречается в безвентиляционных медных инструментах, известных с древних времен, и в гармонических обертонах струнных инструментов.

Значение для дальнейшего развития тональных систем

Дальнейшее исследование интервалов, состоящих из октав, квинт и кварт, и их кратных, в конечном итоге привело от диатонических гамм с семью различными тонами ( гептатоническая гамма ) в пифагорейской настройке к хроматической гамме с двенадцатью тонами. Интервалы вольфа в пифагорейской настройке представляли собой проблему: вместо чистых квинт A♭-E♭ и D♭-A♭ звучали расстроенные пифагорейской коммой квинты G♯-E♭ и C♯-A♭ .

С появлением полифонии во второй половине XV века, в дополнение к октаве и квинте, чистая терция стала решающей для мажорных и минорных трезвучий. Хотя эта настройка не могла быть реализована на двенадцатинольной клавиатуре, она могла быть хорошо достигнута в темперации мидтон. Ее недостатком было то, что не все тональности круга квинт были доступны для игры. Чтобы исправить этот недостаток, были введены темперированные настройки, хотя и с тем компромиссом, что чистая терция звучала резче в некоторых тональностях. В настоящее время большинство инструментов настроены в равномерной темперации с 12 тональностями, так что октавы совершенно чистые, квинты почти чистые, а терции звучат грубо.

Четыре пифагорейских тона в музыке

В музыке четыре гармонических пифагорейских тона играют важную роль в пентатонической гамме, особенно на первой, четвертой, пятой и восьмой ступенях диатонической гаммы (особенно в мажоре и миноре) и в составе каденций как основные тона тоники, субдоминанты и доминанты. Эта последовательность тонов часто появляется в каденциях с соответствующими аккордами:

Аудиопример ^ⓘ Полная каденция в до мажоре с последовательностью ступеней: тоника (до мажор) – субдоминанта (фа мажор) – доминанта (соль мажор) – тоника (до мажор)

Четыре пифагорейских тона появляются во многих композициях. Первые тона средневековых антифонов "Ad te levavi" и "Factus est repente" состоят в основном из четырех пифагорейских тонов, за исключением некоторых украшений и высоких нот. ^[19]

Другой пример — начало Пассакалии до минор Иоганна Себастьяна Баха. Тема состоит из пятнадцати тонов, из которых в общей сложности десять тонов, и особенно последние четыре тона, получены из последовательности.

Опровержение

Абсолютная высота тона молотков
Резонансная частота стальных молотков, которые могут быть перемещены руками человека, обычно находится в ультразвуковом диапазоне и поэтому неслышима. Пифагор не мог воспринимать эти тона, особенно когда молотки имели разницу в одну октаву по высоте тона.

Высота тона в зависимости от веса молотка
Частота колебаний свободно колеблющегося твердого тела, например продольной волны, обычно не пропорциональна его весу или объему, но пропорциональна его длине, которая при аналогичной геометрии изменяется только пропорционально кубическому корню объема.

Для молотов Пифагора применимы следующие коэффициенты отношения для аналогичной геометрии (значения в условных единицах):

Высота тона в зависимости от натяжения струны
Предположение о том, что частота колебаний струны пропорциональна натяжению, неверно. Скорее, частота колебаний пропорциональна квадратному корню натяжения. Чтобы удвоить частоту колебаний, необходимо приложить натяжение в четыре раза больше и, следовательно, на струну необходимо повесить груз в четыре раза тяжелее.

Физические соображения

Созвучие

Целочисленные коэффициенты частот

Тот факт, что тон с основной частотой находится в созвучии со вторым тоном с целым кратным (с и ) этой основной частоты, сразу же очевиден из того факта, что максимумы и минимумы колебаний тона синхронны во времени, но может быть также объяснен следующим образом: ${\displaystyle f_{1}}$ ${\displaystyle {n}}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle {n}>{1}}$ ${\displaystyle f_{2}=n\cdot f_{1}}$

Частота биений двух одновременно звучащих тонов математически рассчитывается из разницы частот этих двух тонов и может быть услышана как комбинированный тон: ${\displaystyle f_{S}}$

${\displaystyle f_{S}=f_{2}-f_{1}}$

(см. Математическое описание ритма ).

Эта разница сама по себе находится в целочисленном отношении к основной частоте : ${\displaystyle f_{1}}$

${\displaystyle {\begin{aligned}f_{S}&=n\cdot f_{1}-f_{1}\\&=(n-1)\cdot f_{1}\end{aligned}}}$

Для всех целых кратных основной частоты во втором тоне существуют также целые кратные частоты биений (см. таблицу справа), так что все тоны звучат консонансно.

Рациональные частотные соотношения

Даже для двух тонов, частоты которых находятся в рациональном отношении к , существует консонанс. Частота второго тона определяется по формуле: ${\displaystyle {(n+1)}}$ ${\displaystyle {n}}$

${\displaystyle f_{2}={\frac {n+1}{n}}\cdot f_{1}}$

Следовательно, частота биений двух одновременно звучащих тонов определяется по формуле:

${\displaystyle {\begin{aligned}\Rightarrow f_{S}&={\frac {n+1}{n}}\cdot f_{1}-f_{1}\\&=(1+{\frac {1}{n}}-1)\cdot f_{1}\\&={\frac {1}{n}}\cdot f_{1}\\\Leftrightarrow n\cdot f_{S}&=f_{1}\end{aligned}}}$

При этом условии основная частота всегда кратна частоте биений (см. таблицу справа). Поэтому диссонанса не возникает.

Продольные колебания и собственная частота твердых тел

Для оценки металлического блока рассмотрим однородную прямоугольную призму максимальной длины , изготовленную из материала со скоростью звука . Для режима колебаний вдоль ее самой длинной стороны ( продольные колебания ) она имеет самую низкую собственную частоту с пучностями на обоих концах и узлом в середине. ^[20] ${\displaystyle {l}}$ ${\displaystyle {v}}$ ${\displaystyle {f}}$

${\displaystyle {f={\frac {v}{2\cdot l}}}}$.

Следовательно, высота тона не зависит от массы и площади поперечного сечения призмы, а площадь поперечного сечения может даже меняться. Более того, сила и скорость при ударе по телу также не играют роли. По крайней мере, этот факт соответствует наблюдению, приписываемому Пифагору, что воспринимаемая высота тона не зависела от рук (и, следовательно, сил) мастеров.

Тела с более сложной геометрией , такие как колокола , чашки или чаши , которые могут быть даже заполнены жидкостями, имеют собственные частоты, которые требуют значительно более сложных физических описаний, поскольку необходимо учитывать не только форму, но и толщину стенки или даже место удара. В этих случаях также могут возбуждаться и быть слышимыми поперечные колебания .

Молотки

Головка кузнечного молота, иллюстрация из американского учебника по ковке 1899 года.

Очень большая кувалда (скорость звука в стали составляет примерно = 5000 метров в секунду) с длиной головки молотка = 0,2 метра имеет собственную частоту 12,5 килогерц. При площади квадратного сечения 0,1 квадратного метра (0,1 метра на 0,1 метра) она имела бы необычно большую массу почти 16 килограммов при плотности 7,86 грамма на кубический сантиметр. Частоты выше примерно 15 килогерц уже не могут восприниматься многими людьми (см. слуховой порог ); поэтому собственная частота такого большого молотка едва слышна. Молотки с более короткими головками имеют еще более высокие собственные частоты, которые поэтому неслышны. ${\displaystyle {v}}$ ${\displaystyle {l}}$

Наковальни

Большая стальная наковальня длиной 0,5 метра имеет собственную частоту всего 5 килогерц и поэтому ее легко услышать. ${\displaystyle {l}}$

Существует множество композиций , в которых композитор указывает на использование наковален в качестве музыкальных инструментов. Особенно известны две оперы из музыкальной драмы « Кольцо нибелунга» Рихарда Вагнера :

• «Золото Рейна» , сцена 3, 18 наковален в фа мажор в трех октавах
• Зигфрид , Акт 1, Кузнечная песня Зигфрида Nothung! Ничего! Нидлихес Шверт!

Материалы с более низкой скоростью звука, чем сталь, такие как гранит или латунь , производят еще более низкие частоты с конгруэнтной геометрией. В любом случае, наковальни не упоминаются в ранних отчетах, а слышимые звуки наковален приписываются молоткам в более поздних версиях легенды.

Металлические стержни

Металлический стержень длиной l и площадью поперечного сечения A

Четыре зубила разной длины (12, 9, 8 и 6 единиц) и одинаковой площади поперечного сечения, вибрирующие вдоль продольной оси с частотами колебаний, пропорциональными длине и массе.
Звуковые примеры зубил с частотами колебаний, которые находятся в целочисленных отношениях друг к другу:

Фундаментальный (длиной 12 ед.)

Четвертый (9 единиц в длину)

Пятый (длиной 8 единиц)

Октава (длиной 6 единиц)

Зубило с нецелым отношением к основному тону ( тритон = ⁠1/2⁠ октава):

Тритон (длиной 8,485 единиц)

Можно сравнить металлические стержни, такие как долота, используемые каменщиками, или клинья для раскалывания камней, чтобы прийти к наблюдению, аналогичному тому, которое приписывается Пифагору, а именно, что частота вибрации инструментов пропорциональна их весу . Если металлические стержни, пренебрегая сужающимися режущими кромками, все имеют одинаковую равномерную площадь поперечного сечения A, но разную длину l , то их вес пропорционален длине и, следовательно, также частоте вибрации, при условии, что металлические стержни возбуждаются продольными колебаниями ударами вдоль продольной оси (звуковые примеры можно найти в поле справа). ^[21]

Для изгибных осцилляторов, таких как камертоны или пластины металлофонов , действуют другие условия и законы; поэтому эти соображения к ним не применимы.

Колебания струн

Принцип монохорда: колеблющаяся струна длиной l и натяжением F между двумя мостиками на резонаторном ящике.

Струны могут быть закреплены на двух концах, каждый на мосту . В отличие от твердого тела с продольными колебаниями, два моста устанавливают граничные условия для двух узловых точек колебаний; следовательно, узел колебаний находится посередине.

Собственная частота и, следовательно, высота тона струн с длиной не пропорциональны натяжению , а квадратному корню натяжения. Более того, частота увеличивается с более высоким натяжением и, следовательно, более высоким натяжением, а не уменьшается: ^[22] ${\displaystyle {f}}$ ${\displaystyle {l}}$ ${\displaystyle {F}}$

${\displaystyle f\propto {\frac {\sqrt {F}}{l}}}$

Тем не менее, частота колебаний обратно пропорциональна длине струны при постоянном натяжении, что можно напрямую продемонстрировать на примере монохорда , предположительно изобретенного Пифагором.

Прием

Хронология: Авторы, передающие версии легенды о кузнице ( зеленый ). Философы, отмеченные синим цветом, занимались взаимосвязью математики и музыки.

Древность

Самое раннее упоминание об открытии Пифагором математической основы музыкальных интервалов встречается у платоника Ксенократа (IV в. до н. э.); поскольку это всего лишь цитата из утерянного труда этого мыслителя, неясно, знал ли он легенду о кузнице. ^[23] В IV в. до н. э. уже высказывалась критика пифагорейской теории интервалов, хотя и без ссылки на легенду о Пифагоре; философ и теоретик музыки Аристоксен считал ее ложной.

Никомах из Герасы на средневековом изображении XII века, Университетская библиотека Кембриджа, Ms. Ii.3.12, fol. 61 v

Самая старая записанная версия легенды была представлена ​​столетиями позже времени Пифагора неопифагорейцем Никомахом из Герасы , который в 1-м или 2-м веке нашей эры задокументировал историю в своем Harmonikḗ Encheirídion («Справочник гармонии»). Он опирался на философа Филолая , пифагорейца V века до нашей эры, для его представления числовых соотношений в теории музыки. ^[24]

Известный математик и теоретик музыки Птолемей (II в. н. э.) знал о методе веса, переданном легендой, но отверг его. Однако он не признавал ложность экспериментов с весом; он лишь критиковал их неточности по сравнению с точными измерениями на монохорде. ^[25] Вероятно, что он получил свои знания о легендарной традиции не от Никомаха, а из более древнего источника, ныне утерянного. ^[26]

Теоретик музыки эпохи Империи, хронологически трудно устанавливаемый, Гауденций , описал легенду в своем труде Harmonikḗ Eisagōgḗ («Введение в гармонию»), в версии, немного короче, чем у Никомаха. Философ- неоплатоник Ямвлих из Халкиды , работавший учителем философии в конце III и начале IV веков, написал биографию Пифагора под названием « О пифагорейской жизни» , в которой он воспроизвел легенду о кузнеце в версии Никомаха.

В первой половине V века писатель Макробий подробно обсуждал легенду о кузнецах в своем комментарии к « Сну Сципиона » Цицерона , которую он описал в той же манере, что и Никомах. ^[27]

Боэций (слева) соревнуется с Пифагором (справа, с абаком). Картина Грегора Рейша, изображающая аллегорическую женскую фигуру, несущую две книги, и надпись Typus arithmeticae , Margarita philosophica , 1508

Самый сильный резонанс среди античных теоретиков музыки, которые взялись за повествование, был достигнут Боэцием с его учебником De Establishe musica («Введение в музыку»), написанным в начале VI века, в котором он сначала описывает усилия Пифагора по пониманию в кузнице, а затем дома. ^[28] Неясно, опирался ли он на рассказ Никомаха или на другой источник. В отличие от всей более ранней традиции, он сообщает о пяти молотах вместо четырех, предполагаемых более ранними авторами. Он утверждает, что Пифагор отверг пятый молот, потому что он приводил к диссонансу со всеми остальными молотами. Согласно рассказу Боэция (как и у Макробия), Пифагор проверил свое первоначальное предположение о том, что разница в звуке была вызвана разной силой в руках людей, заставив кузнецов обменяться молотами, что привело к его опровержению. Относительно экспериментов в доме Пифагора Боэций пишет, что философ сначала подвесил нити с весами, равными весу молотков в кузнице, а затем экспериментировал с трубками и чашами, причем все эксперименты давали те же результаты, что и первоначальные с молотками. Используя легенду в качестве основы, Боэций рассматривает вопрос о надежности чувственных восприятий с точки зрения науки и эпистемологии. Важнейшим моментом является то, что Пифагор изначально был побужден чувственным восприятием к формулированию своего вопроса и гипотез, и путем эмпирической проверки гипотез он пришел к неопровержимой уверенности. Путь к знанию шел от чувственного восприятия к первоначальной гипотезе, которая оказалась ошибочной, затем к формированию правильного мнения и, наконец, к его проверке. Боэций признает необходимость и ценность чувственного восприятия и формирования мнения на пути к прозрению, хотя как платоник он изначально скептически относится к чувственному восприятию из-за его склонности к ошибкам. Подлинное знание, по его мнению, возникает только тогда, когда регулярность схвачена, что позволяет исследователю освободиться от своей изначальной зависимости от ненадежного чувственного восприятия. Суждение исследователя не должно основываться исключительно на чувственном суждении, полученном из эмпирического опыта, но скорее оно должно быть сделано только после того, как они нашли правило путем размышления, которое позволяет им позиционировать себя за пределами области возможного сенсорного обмана. ^[29]

В VI веке ученый Кассиодор в своих «Институциях» писал , что Гауденций приписывал начало «музыки» Пифагору в своем рассказе о легенде о кузнеце. Он имел в виду теорию музыки, как и Ямвлих, который, ссылаясь на рассказ о кузнеце и описанные там эксперименты, называл Пифагора изобретателем «музыки». ^[30]

Средний возраст

В раннем Средневековье Исидор Севильский упомянул легенду о кузнеце в своей работе Etymologiae , которая стала фундаментальным справочным трудом для образованных людей в Средние века. Он кратко упомянул легенду, приняв формулировку Кассиодора, а также обозначив Пифагора как изобретателя музыки. ^[31] Поскольку Кассиодор и Исидор были первоклассными авторитетами в Средние века, распространилось представление о том, что Пифагор открыл основной закон музыки и, таким образом, был ее основателем. Несмотря на такие огульные заявления, средневековые теоретики музыки предполагали, что музыка существовала до Пифагора и что «изобретение музыки» относилось к открытию ее принципов. ^[32]

В IX веке музыковед Аврелиан из Реоме пересказал легенду в своей работе Musica disciplina («Теория музыки»). Рассказ Аврелиана был продолжен в X веке Регино из Прюма в его работе De harmonica Establishe («Введение в теорию гармонии»). Оба подчеркивали, что Пифагору была предоставлена ​​возможность сделать свое открытие в кузнице благодаря божественному провидению. ^[33] В древности Никомах и Ямвлих уже говорили о демоническом провидении, а Боэций превратил его в божественное повеление.

В XI веке легендарный материал был обработан в Carmina Cantabrigiensia . ^[34]

Гвидо из Ареццо (слева) дает указания епископу играть на монохорде. Вена, Австрийская национальная библиотека , Codex Lat. 51, fol. 35v (XII век)

В первой половине XI века Гвидо из Ареццо , самый известный теоретик музыки Средневековья, рассказал легенду о кузнеце в последней главе своего «Микролога» , основываясь на версии Боэция, которого он назвал конкретно. Гвидо заметил в начале: Никто бы никогда не открыл ничего определенного об этом искусстве (музыке), если бы, в конце концов, божественная благость не вызвала следующее событие по своему велению. Он приписал тот факт, что молоты весили 12, 9, 8 и 6 единиц и, таким образом, производили гармоничный звук, Божьему провидению. ^[35] Он также упомянул, что Пифагор, исходя из своего открытия, изобрел монохорд, но не вдавался в подробности о его свойствах.

Работа «De musica» Иоганнеса Котто (также известного как Джон Коттон или Иоганнес Аффлигеменсис) была проиллюстрирована сценой кузнечного дела около 1250 года анонимным иллюстратором книг в цистерцианском аббатстве Альдерсбах . ^[36]

Среди средневековых теоретиков музыки, которые пересказывали легенду о кузнице согласно версии Боэция, были также Хуан Хиль де Самора (Иоганнес Эгидиус фон Самора), творивший в конце XIII — начале XIV веков, Иоганнес де Мурис и Симон Тунстеде в XIV веке, а также Адам фон Фульда на пороге раннего Нового времени в XV веке.

Как противник пифагорейской концепции, которая считала, что консонансы основаны на определенных числовых соотношениях, Иоганнес де Грохейо появился в 13 веке, начиная с аристотелевской точки зрения. Хотя он прямо заявил, что Пифагор открыл принципы музыки, и рассказал легенду о кузнице, ссылаясь на Боэция, которого он считал заслуживающим доверия, он отверг пифагорейскую теорию консонанса, которую он хотел свести к чисто метафорическому выражению. ^[37]

Ранний современный период

Франкино Гаффурио, «Theorica musice» (1492): библейский изобретатель музыки, Джубал , с шестью кузнецами вокруг наковальни (вверху слева); Пифагор экспериментирует с шестью колокольчиками и шестью стаканами (вверху справа), с шестью струнами (внизу слева) и вместе с Филолаем с шестью флейтами (внизу справа)

Иллюстрация четырех пифагорейских молотов с весовым соотношением 12:9:8:6, согласно математику Генриху Шрайберу в книге Ayn new kunstlich Buech welches gar gewiss vnd behend lernet nach der gemainen Regel detre Grammateum oder Schreyber , опубликованной в 1521 году. .

Франкино Гаффурио опубликовал свою работу Theoricum opus musice discipline («Теоретическая теория музыки») в Неаполе в 1480 году, которая была пересмотрена и переиздана в 1492 году под названием Theorica musice («Теория музыки»). В ней он представил версию легенды о кузнице, которая превзошла все предыдущие описания по детализации. Он основал свою версию на версии Боэция и добавил шестой молот, чтобы включить в повествование как можно больше тонов октавы. В четырех графических изображениях он представил музыкальные инструменты или звуковые генераторы, каждый с шестью гармоническими тонами, и указал числа 4, 6, 8, 9, 12 и 16, связанные с тонами в этикетках. В дополнение к четырем традиционным соотношениям легенды (6, 8, 9 и 12) он добавил 4 и 16, которые представляют тон на квинту ниже и другой тон на кварту выше. Вся последовательность тонов теперь простирается не только на одну, но и на две октавы. Эти числа соответствуют, например, тонам f – c' – f' – g' – c" – f":

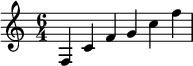
В 1546 году художнику Эрхарду Зансдорферу было поручено создать фреску в гессенском замке Бюдинген, которая хорошо сохранилась и представляет собой своего рода компендиум, представляющий историю музыки, начиная с кузницы Пифагора. ^[38]

Джозеффо Царлино также пересказал легенду в своей работе Le istitutioni harmoniche («Основы гармонии»), которую он опубликовал в 1558 году; как и Гаффурио, он основывал свой рассказ на версии Боэция. ^[39]

Теоретик музыки Винченцо Галилей, отец Галилео Галилея, в 1589 году опубликовал трактат Discorso intorno all'opere di messer Gioseffo Zarlino («Рассуждение о трудах господина Джозеффо Зарлино»), который был направлен против взглядов его учителя Зарлино. В нем он указал, что сведения в легенде о нагружении струн грузами неточны.[1]

Гравюра на меди «Дюнкирхен» Эберхарда Кизера

В 1626 году в Thesaurus philopoliticus Даниэля Мейснера была представлена ​​медная гравюра под названием «Duynkirchen» Эберхарда Кизера, изображающая всего трех кузнецов у наковальни. Подпись на латыни и немецком гласит:[2]

Triplicibus percussa sonat varie ictibus incus.

Музыка Пифагора строится по принципу фундамента (eps).

Наковальня издает тройные удары, производя три разных тона.

Музыка — это фундамент, заложенный Пифагором, который не под силу создать даже ослиной голове.

Несколько лет спустя вопрос окончательно прояснился после того, как Галилео Галилей и Марин Мерсенн открыли законы колебаний струн. В 1636 году Мерсенн опубликовал свою Harmonie universelle, в которой объяснил физическую ошибку в легенде: частота колебаний пропорциональна не натяжению, а его квадратному корню.[3]

Несколько композиторов включили эту тему в свои произведения, в том числе Георг Муффат в конце XVII века. ^[40] и Руперт Игнац Майр . ^[41]

Современная эпоха

Еще в XIX веке Гегель в своих лекциях по истории философии предполагал физическую точность предполагаемых измерений, упомянутых в легенде о Пифагоре. ^[42]

Вернер Гейзенберг подчеркнул в эссе, впервые опубликованном в 1937 году, что пифагорейское «открытие математической определенности гармонии» основано на «идее осмысленной силы математических структур», «фундаментальной идее, которую современная точная наука унаследовала от античности»; открытие, приписываемое Пифагору, принадлежит «к сильнейшим импульсам человеческой науки в целом». ^[43]

Совсем недавно были опубликованы отчеты, в которых легенда некритически воспроизводилась без ссылки на ее физическую и историческую ложность. ^[44] Например, в научно-популярной книге « Пятый молот: Пифагор и дисгармония мира» Даниэля Хеллера-Роазена . ^[45]

Источники

• Готфрид Фридлейн (герс.): Аникии Манлии Торкуати Северини Боэтии де институции арифметических библиотек дуэта, де институции музыкальных библиотек quinque. Минерва, Франкфурт-на-Майне, 1966 (Nachdruck der Ausgabe Leipzig 1867, онлайн; deutsche Übersetzung онлайн)
• Михаэль Гермесдорф (Übersetzer): Micrologus Guidonis de disciplina artis musicae, di Kurze Abhandlung Guidos über die Regeln der musikalischen Kunst . Трир 1876 г. (онлайн)
• Ильде Иллюминаты, Фабио Беллиссима (Hrsg.): Франчино Гаффурио: Theorica musice. Edizioni del Galluzzo, Firenze, 2005, ISBN  88-8450-161-X , S. 66–71 (lateinischer Text und italienische Übersetzung)

Дальнейшее чтение

• Вальтер Буркерт: Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon (= Erlanger Beiträge zur Sprach- und Kunstwissenschaft . Группа 10). Ганс Карл, Нюрнберг, 1962 г.
• Аня Хайльманн: Musiktheorie und das Quadrivium Боэция. Eine Einführung in den neuplatonischen Hintergrund von "De Institutione Musica" . Vandenhoeck & Ruprecht, Göttingen 2007, ISBN 978-3-525-25268-0 , S. 203–222 ( [1] в Google Книгах ) 
• Вернер Кайль (Hrsg): Basistexte Musikästhetik und Musiktheorie. Вильгельм Финк, Падерборн, 2007 г., ISBN 978-3-8252-8359-9 , S. 342–346 ( [2] в Google Книгах ) 
• Барбара Мюнксельхаус: Музыкальный Пифагор. Zur Rezeption der pythagoreischen Musiktheorie als Quadrivialer Wissenschaft im lateinischen Mittelalter (= Orpheus-Schriftenreihe zu Grundfragen der Musik . Band 19). Verlag für systematische Musikwissenschaft, Бонн – Бад-Годесберг, 1976 г.
• Йорген Раастед: Забытая версия анекдота об эксперименте Пифагора с молотком. В: Cahiers de l'Institut du Moyen-Âge grec et latin . Полоса 31а, 1979, С. 1–9.
• Леонид Жмудь: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus. Akademie Verlag, Берлин, 1997, ISBN 3-05-003090-9. 

Смотрите также

• Только интонация

Ссылки

1. Вайс, Пьеро и Ричард Тарускин, ред. Музыка в западном мире: история в документах . 2-е изд. Np: Thomson Schirmer, 1984. 3. ISBN 9780534585990 . 
2. Кеннет Сильван Гатри, Дэвид Р. Фиделер (1987). Пифагорейский справочник и библиотека: антология древних сочинений, относящихся к Пифагору и пифагорейской философии , стр. 24. Red Wheel/Weiser. ISBN 9780933999510 . 
3. Кристенсен, Томас, ред. Кембриджская история западной музыкальной теории . Кембридж: Cambridge University Press, 2002. 143. ISBN 9780521623711 . 
4. Буркерт, Уолтер (1972). Знание и наука в древнем пифагореизме , стр.375. ISBN 9780674539181 . Цитируется по Кристенсену, 2002 г., стр. 143. 
5. Маркус Бауч: Über die pythagoreischen Wurzeln der gregorianischen Modi, английский: О пифагорейских корнях григорианских модусов , Mater Dolorosa (Берлин-Ланквиц) , март 2012 г., получено 31 августа 2017 г.
6. Баркер (2004). Эндрю (ред.). Греческие музыкальные сочинения (1-е изд.). Кембридж: Cambridge University Press . стр. 30. ISBN 978-0-521-61697-3.
7. Лукас Н. Х. Бунт; Филлип С. Джонс; Джек Д. Бедиент (1988). Исторические корни элементарной математики (Переиздание). Нью-Йорк: Dover Publications . стр. 72. ISBN 978-0-486-25563-7.
8. Кристиан, Джеймс (26 января 2011 г.). Философия. Введение в искусство удивления. Wadsworth Pub Co. стр. 517. ISBN 978-1-111-29808-1.
9. Waterfield, перевод с комментариями Робина (2000). Первые философы: досократики и софисты (1-е издание как классика Оксфорда в мягкой обложке). Оксфорд: Oxford Univ. Press. стр. 103. ISBN 978-0-19-282454-7. пифагорейцы построили всю вселенную из чисел.
10. "GUIMICB_MBBR2784". chmtl.indiana.edu . Проверено 9 мая 2023 г. Erant antiquitus Instrumenta Incerta. et canentium multitudo sed ceca. Nullus enim hominum uocum дифференциации. et simphoniae Descriptionem Poterat Aliqua Argumentatione Colligere. neque posset unquam certum aliquid de hac arte cognoscere. nisi diuina pietas tandem quod sequitur suo nutu disponeret. Cum Phitagoras quidam magnus philosophus forte iter ageret. uentum est ad Fabricam. in qua super unam incudem quinque Mallei Feriebant. Quorum suauem miratus concordiam philosophus accessit. primumque in manuum uarietate sperans [f.20r] uim soni ac modulationis существует. мутауит маллеос. Quo факто. sua uis quemque secuta est. Subtracto itaque uno qui dissonus при прочих равных условиях. Алиос пондероит. Mirumque in modum diuino nutu primus .XII. секундус .VIIII. терциус .VIII. квартус .VI. nescio quibus ponderibus Appendebant. Cognouit itaque в пропорциях и подборке музыкальных произведений uersari scientiam. Erat enim ea constitutio in quattuor malleis. quae modo est in quattuor Litteris .ADEA Denique si A habeat .XII. и др. VIIII. sintque quaternarii in pro passu. хабебит .А. в .XII. тернарии .IIII. и др. в .VIIII. тернариос .III. Ecce diatessaron. Rursus cum habeat A .XII. si teneat E. VIII. кватернариос passus tres habebit .A. дуос уэро Э. и др. диапенте патент. Sint iterum .XII в A. et .VI. в альтераме а. Сенарий медиетас эст дуоденарий. sicut et a acuta alterius A medietate coligitur. Адест, следовательно, диапазон. Cum igitur ipsa .a. ad D. diatessaron ad e diapente. изменить свой диапазон Reddit. D quoque ad e tonum. ad utrumque А диатессарон. et dipente sonat. Et E etiam ad D. tonum utrique Aa dipente et diatessaron mandat. a uero acuta cum a range. включая D диапенте. cum E сонат диатессарона. quae in supra dictis numeris curiosus perscrutator inuenit. Hinc enim incipiens Boetius panditor huius artis. multam miramque et difficillimam huius artis cum numerorum пропорциональная согласительная демонстрация. [f.20v] Quid plura? Per supra dictas виды uoces ordinans. monocordum primus ille Phitagoras quattuor neruorum comosuit. in quo quia no est lasciuia. sed diligenter aperta artis notitia. sapientibus в коммуне placuit. atque usque in hunc diem ars paulatim crescendo conualuit. ipso Doctore Semper Humanas Tenebras illustrante. cuius summa sapientia per cuncta uiget secula.
11. Никомах фон Гераса, Справочник по гармонике 6, перевод Ани Хайльманн: Теория музыки Боэция и квадривиум , Гёттинген 2007, стр. 345–347, дословно цитируется в Ямвлих фон Халкис, О пифагорейской жизни 115–121, перевод Михаэля фон Альбрехта: Ямвлих. Пифагор: Легенда – Доктрина – Образ жизни , Дармштадт 2002, стр. 109–113.
12. Вальтер Буркерт: Weisheit und Wissenschaft , Нюрнберг, 1962, с. 353 и примечание 28.
13. Леонид Жмудь: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus , Берлин, 1997, стр. 193–196; см. также Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, стр. 28 f.
14. Вальтер Буркерт: Weisheit und Wissenschaft , Нюрнберг, 1962, стр. 362–364; Леонид Жмудь: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus , Берлин, 1997, стр. 196–199. Скептицизм относительно акустических экспериментов Архитаса выражен Карлом А. Хаффманом : Archytas of Tarentum , Cambridge, 2005, стр. 129–148; см. также стр. 473–475. Он указывает, что Архит в основном опирается на сведения своих предшественников и житейский опыт.
15. Вальтер Буркерт: Weisheit und Wissenschaft , Нюрнберг, 1962, с. 355.
16. Вальтер Буркерт: Weisheit und Wissenschaft , Нюрнберг, 1962, с. 355; Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, стр. 38 f., 46.
17. Джеймс В. Маккиннон: Джубал и Пифагор, кто изобретатель музыки? В: The Musical Quarterly , vol. 64, нет. 1, 1978, стр. 1–28; Пол Э. Байхнер: средневековый представитель музыки, Джубал или Тубалкаин? (= Тексты и исследования по истории средневекового образования 2), Нотр-Дам, Индиана, 1954; Франсис Оливье Циммерман: Кузница и гармония. Пифагор к Тубалкаину и Ювалу. В: Циммерманн: Орфея: живое искусство, условно-досрочное освобождение и мелодия (онлайн).
18. Йорген Раастед: «Забытая версия анекдота об эксперименте Пифагора с молотком». В: Cahiers de l'Institut du Moyen-Âge grec et latin 31a, 1979, стр. 1–9, здесь: 6 сл.; Леонид Жмудь: «Wissenschaft, Philosophie und Religion im frühen Pythagoreismus», Берлин, 1997, с. 192. (Перевод с немецкого)
19. См. Factus est repente, Отношения слова и мелодии в григорианском пении; Der erste Gesang des Kirchenjahres.
20. Людвиг Бергманн, Клеменс Шефер: Lehrbuch der Experimental Physics. Полоса 1, 9. Ауфляж. Берлин, 1974, Глава 83: Schallsender , Abschnitt Longitudinalschwingungen .
21. Маркус Бауч: Über die pythagoreischen Wurzeln der gregorianischen Modi (онлайн).
22. Людвиг Бергманн, Клеменс Шефер: Lehrbuch der Experimental Physics. Полоса 1, 9. Ауфляж. Берлин, 1974, Глава 83: Schallsender , Abschnitt Saite .
23. Ксенократ Фрагмент 9 H. См. Walter Burkert: Weisheit und Wissenschaft , Нюрнберг, 1962, стр. 10. 57 и Леонид Жмудь: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus , Берлин, 1997, с. 193.
24. Этот отрывок из труда Никомаха отредактирован, переведен на английский язык и прокомментирован Карлом А. Хаффманом: Филолай Кротонский , Кембридж, 1993, стр. 145–165.
25. Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, с. 52.
26. Вальтер Буркерт: Weisheit und Wissenschaft , Нюрнберг, 1962, с. 355.
27. Макробий, Комментарии в somnium Scipionis 2,1,8–13.
28. Боэций, De Institutione Musica 1,10–11, перевод Ани Хейльманн: Musiktheorie und das Quadrivium Боэция , Геттинген, 2007, стр. 342–345.
29. Научную и эпистемологическую основу см. Аня Хайльманн: Musiktheorie und das Quadrivium Боэция , Геттинген, 2007, стр. 205–218.
30. Кассиодор, Institutiones 2,5,1; ср. Ямвлих, De vita Pythagorica 121.
31. Исидор, Этимологии 3,16,1.
32. Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, стр. 15–17.
33. Ганс Мартин Клинкенберг: Der Verfall des Quadriviums im frühen Mittelalter. В: Йозеф Кох (ред.): Artes liberes. Von der antiken Bildung zur Wissenschaft des Mittelalters , Лейден, 1976, стр. 1–32, здесь: 24 f.
34. Carmina Cantabrigiensia , Песнь 45 и последовательность Пифагора (первая половина XI века); см. Вальтер Кранц: Пифагор в Carmina Cantabrigiensia (онлайн; PDF; 2,3 МБ).
35. Гвидо из Ареццо, Micrologus 20 (немецкий перевод онлайн).
36. Рукопись из собрания Альдерсбаха, Clm 2599, л. 96v, Баварская государственная библиотека, Мюнхен
37. Барбара Мюнксельхаус: Pythagoras musicus , Бонн – Бад-Годесберг, 1976, с. 16, 76; Франк Хентшель: Sinnlichkeit und Vernunft in der mittelalterlichen Musiktheorie , Штутгарт, 2000, стр. 148–150 (онлайн).
38. Вальтер Салмен : Musikleben im 16. Jahrhundert (Музыкальная жизнь в 16 веке), Лейпциг, 1976; черно-белая фотография в Интернете.
39. Вернер Кейл (ред.): Basistexte Musikästhetik und Musiktheorie (Основные тексты по музыкальной эстетике и теории музыки), Paderborn 2007, стр. 56 (перевод текста Зарлино).
40. Георг Мюффа: Nova Cyclopeias Harmonica (1690).
41. Руперт Игнац Майр: Пифагоровы Шмидс-Фюнкляйн (1692).
42. Вернер Кейл (ред.): Basistexte Musikästhetik und Musiktheorie , Падерборн, 2007, стр. 343.
43. Вернер Гейзенберг: Gedanken der antiken Naturphilosophie in der Contemporary Physik . В: Вернер Гейзенберг: Wandlungen in den Grundlagen der Naturwissenschaft , 8-е издание, Штутгарт, 1949, стр. 47–53, здесь: 50.
44. Арнольд Кейзерлинг: Geschichte der Denkstile. 3. Das logische Denken (онлайн); Карл Шумередер: Музыка и математика (онлайн); Арнольд Кейзерлинг: Новое имя получило. Die Weltformel und ihre Analogien in der Wirklichkeit , Вена, 2002 г., с. 71 ( Молоты Пифагора , стр. 71, в Google Books ).
45. Даниэль Хеллер-Роазен: Пятый молот: Пифагор и дисгармония мира , Франкфурт-на-Майне 2014, стр. 14–22 (онлайн).