
В численном анализе восхождение на вершину — это математический метод оптимизации , который принадлежит к семейству локального поиска . Это итеративный алгоритм , который начинается с произвольного решения проблемы, а затем пытается найти лучшее решение, внося в решение пошаговые изменения. Если изменение приводит к лучшему решению, в новое решение вносится еще одно пошаговое изменение, и так далее, пока не будет найдено никаких дальнейших улучшений.
Например, восхождение на холм можно применить к задаче коммивояжера . Легко найти начальное решение, которое посещает все города, но, скорее всего, будет очень плохим по сравнению с оптимальным решением. Алгоритм начинается с такого решения и вносит в него небольшие улучшения, например, меняет порядок посещения двух городов. В конечном итоге, скорее всего, будет получен гораздо более короткий маршрут.
Метод восхождения на холм находит оптимальные решения для выпуклых задач — для других задач он найдет только локальные оптимумы (решения, которые не могут быть улучшены никакими соседними конфигурациями), которые не обязательно являются наилучшим возможным решением ( глобальным оптимумом ) из всех возможных решений ( пространство поиска ). Примерами алгоритмов, которые решают выпуклые задачи методом восхождения на холм, являются симплексный алгоритм для линейного программирования и двоичного поиска . [1] : 253 Чтобы попытаться избежать застревания в локальных оптимумах, можно использовать перезапуски (т. е. повторный локальный поиск) или более сложные схемы, основанные на итерациях (например, итерированный локальный поиск ), или на памяти (например, реактивная поисковая оптимизация и поиск с запретами ), или на стохастических модификациях без памяти (например, имитация отжига ).
Относительная простота алгоритма делает его популярным первым выбором среди алгоритмов оптимизации. Он широко используется в искусственном интеллекте для достижения целевого состояния из начального узла. В связанных алгоритмах используются различные варианты выбора следующих узлов и начальных узлов. Хотя более продвинутые алгоритмы, такие как имитация отжига или поиск с запретами, могут давать лучшие результаты, в некоторых ситуациях поиск по холму работает так же хорошо. Поиск по холму часто может давать лучший результат, чем другие алгоритмы, когда количество времени, доступного для выполнения поиска, ограничено, например, в системах реального времени, при условии, что небольшое количество приращений обычно сходится к хорошему решению (оптимальному решению или близкому приближению). С другой стороны, пузырьковую сортировку можно рассматривать как алгоритм поиска по холму (каждый обмен соседними элементами уменьшает количество неупорядоченных пар элементов), однако этот подход далек от эффективности даже для скромного N, поскольку количество требуемых обменов растет квадратично.
Алгоритм «Подъем на холм» является алгоритмом, который может работать в любое время : он может вернуть допустимое решение, даже если его прервут в любой момент до его завершения.
Подъем на холм пытается максимизировать (или минимизировать) целевую функцию , где — вектор непрерывных и/или дискретных значений. На каждой итерации подъем на холм будет корректировать один элемент в и определять, улучшает ли изменение значение . (Обратите внимание, что это отличается от методов градиентного спуска , которые корректируют все значения в на каждой итерации в соответствии с градиентом холма.) При подъеме на холм любое улучшающее изменение принимается, и процесс продолжается до тех пор, пока не будет найдено никаких изменений для улучшения значения . Тогда говорят, что это «локально оптимально».
В дискретных векторных пространствах каждое возможное значение для может быть визуализировано как вершина в графе . Подъем на холм будет следовать по графу от вершины к вершине, всегда локально увеличивая (или уменьшая) значение , пока не будет достигнут локальный максимум (или локальный минимум ) .
В простом восхождении на холм выбирается первый более близкий узел, тогда как в восхождении на холм с самым крутым подъемом сравниваются все последующие узлы и выбирается наиболее близкий к решению. Обе формы терпят неудачу, если нет более близкого узла, что может произойти, если в пространстве поиска есть локальные максимумы, которые не являются решениями. Восхождение на холм с самым крутым подъемом похоже на поиск с лучшим первым , который пробует все возможные расширения текущего пути вместо одного. [2]
Стохастический подъем на холм не проверяет всех соседей перед тем, как решить, как двигаться. Вместо этого он выбирает соседа случайным образом и решает (на основе величины улучшения у этого соседа), следует ли двигаться к этому соседу или проверять другого.
Координатный спуск выполняет линейный поиск вдоль одного координатного направления в текущей точке в каждой итерации. Некоторые версии координатного спуска случайным образом выбирают другое координатное направление в каждой итерации.
Случайный перезапуск восхождения на холм — это мета-алгоритм, построенный поверх алгоритма восхождения на холм. Он также известен как восхождение на холм дробовиком . Он итеративно выполняет восхождение на холм, каждый раз со случайным начальным условием . Лучшее сохраняется: если новый запуск восхождения на холм дает лучшее, чем сохраненное состояние, он заменяет сохраненное состояние.
Случайный перезапуск восхождения на холм — удивительно эффективный алгоритм во многих случаях. Оказывается, что часто лучше потратить процессорное время на исследование пространства, чем тщательно оптимизировать исходное состояние. [ оригинальное исследование? ]
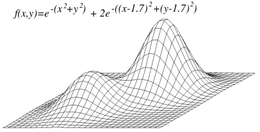
Hill climbing не обязательно найдет глобальный максимум, но вместо этого может сойтись на локальном максимуме . Эта проблема не возникает, если эвристика выпуклая. Однако, поскольку многие функции не являются выпуклыми, hill climbing часто может не достичь глобального максимума. Другие алгоритмы локального поиска пытаются преодолеть эту проблему, такие как стохастический hill climbing , случайные блуждания и имитация отжига .
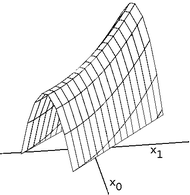
Гребни представляют собой сложную проблему для скалолазов, которые оптимизируют в непрерывных пространствах. Поскольку скалолазы изменяют только один элемент вектора за раз, каждый шаг будет двигаться в направлении, выровненном по оси. Если целевая функция создает узкий гребень, который поднимается в направлении, не выровненном по оси (или если цель состоит в минимизации, узкий переулок, который спускается в направлении, не выровненном по оси), то скалолаз может подняться на гребень (или спуститься по переулку) только зигзагом. Если стороны гребня (или переулка) очень крутые, то скалолаз может быть вынужден делать очень маленькие шаги, поскольку он зигзагом движется к лучшему положению. Таким образом, для подъема на гребень (или спуска по переулку) может потребоваться неоправданно много времени.
Напротив, методы градиентного спуска могут двигаться в любом направлении, в котором гребень или переулок могут подниматься или опускаться. Следовательно, градиентный спуск или метод сопряженного градиента обычно предпочтительнее, чем метод восхождения на холм, когда целевая функция дифференцируема. Однако методы восхождения на холм имеют то преимущество, что не требуют, чтобы целевая функция была дифференцируемой, поэтому методы восхождения на холм могут быть предпочтительны, когда целевая функция сложная.
Другая проблема, которая иногда возникает при восхождении на холм, — это плато. Плато встречается, когда пространство поиска плоское или достаточно плоское, так что значение, возвращаемое целевой функцией, неотличимо от значения, возвращаемого для соседних регионов из-за точности, используемой машиной для представления ее значения. В таких случаях восхождение на холм может оказаться не в состоянии определить, в каком направлении ему следует двигаться, и может блуждать в направлении, которое никогда не приведет к улучшению.
Алгоритм псевдокода Discrete Space Hill Climbing — это текущийУзел := начальныйУзел цикл сделать L := СОСЕДИ(текущийУзел) nextEval := −INF следующийУзел := NULL для всех x в L сделать , если EVAL(x) > nextEval тогда следующийУзел := x nextEval := EVAL(x) если nextEval ≤ EVAL(currentNode), то // Возвращаем текущий узел, так как лучших соседей не существует возврат текущего узла текущийУзел := следующийУзел
алгоритм Непрерывное восхождение на космический холм currentPoint := initialPoint // вектор нулевой величины является общим stepSize := initialStepSizes // вектор, состоящий из всех единиц, является общим ускорение := someAcceleration // обычное значение, например 1,2 кандидат[0] := −ускорение кандидат[1] := −1 / ускорение кандидат[2] := 1 / ускорение кандидат[3] := ускорение bestScore := EVAL(currentPoint) цикл сделать доОценка := лучшаяОценка для каждого элемента i в currentPoint сделать доТочки := текущаяТочка[i] лучшийШаг := 0 для j от 0 до 3 do // попробовать каждое из 4 возможных местоположений шаг := размер_шага[i] × кандидат[j] currentPoint[i] := beforePoint + шаг оценка := EVAL(текущая_точка) если оценка > bestScore тогда bestScore := оценка лучшийШаг := шаг если bestStep равен 0, то currentPoint[i] := beforePoint stepSize[i] := stepSize[i] / ускорение еще currentPoint[i] := beforePoint + bestStep stepSize[i] := bestStep // ускорение если (лучший счет − до счета) < эпсилон , то вернуть текущую точку
Контрастный генетический алгоритм ; случайная оптимизация .