В физике принцип локальности гласит, что на объект напрямую влияет только его непосредственное окружение. Теория, включающая принцип локальности, называется «локальной теорией». Это альтернатива концепции мгновенного или «нелокального» действия на расстоянии . Локальность развилась из полевых теорий классической физики . Идея заключается в том, что для того, чтобы причина в одной точке имела эффект в другой точке, что-то в пространстве между этими точками должно опосредовать действие. Чтобы оказать влияние, что-то, например волна или частица, должно пройти через пространство между двумя точками, неся влияние.
Специальная теория относительности ограничивает максимальную скорость, с которой может распространяться причинное влияние, скоростью света , . Следовательно, принцип локальности подразумевает, что событие в одной точке не может вызвать действительно одновременный результат в другой точке. Событие в точке не может вызвать результат в точке за время, меньшее , где — расстояние между точками, а — скорость света в вакууме.
Принцип локальности играет решающую роль в одном из центральных результатов квантовой механики. В 1935 году Альберт Эйнштейн , Борис Подольский и Натан Розен с их мысленным экспериментом парадокса ЭПР выдвинули возможность того, что квантовая механика может быть не полной теорией. Они описали две системы, физически разделенные после взаимодействия; эта пара будет называться запутанной в современной терминологии. Они рассуждали, что без дополнений, которые теперь называются скрытыми переменными , квантовая механика предсказывала бы нелогичные отношения между физически разделенными измерениями.
В 1964 году Джон Стюарт Белл сформулировал теорему Белла , неравенство, которое, если нарушается в реальных экспериментах, подразумевает, что квантовая механика нарушает локальную причинность (называемое в более поздних работах локальным реализмом), результат, который теперь считается эквивалентным исключению локальных скрытых переменных . Прогрессивные вариации этих тестовых экспериментов Белла с тех пор показали, что квантовая механика в целом нарушает неравенства Белла. Согласно некоторым интерпретациям квантовой механики , этот результат подразумевает, что некоторые квантовые эффекты нарушают принцип локальности.
В XVII веке принцип всемирного тяготения Ньютона был сформулирован в терминах «действия на расстоянии», тем самым нарушая принцип локальности. Сам Ньютон считал это нарушение абсурдным:
Немыслимо, чтобы неодушевленная Материя могла, без посредничества чего-то еще, что не является материальным, воздействовать на другую материю и влиять на нее без взаимного контакта... То, что Гравитация должна быть врожденной, неотъемлемой и неотъемлемой для Материи, так что одно тело может воздействовать на другое на расстоянии через Вакуум, без посредничества чего-либо еще, посредством которого их Действие и Сила могут передаваться от одного к другому, для меня является таким большим Абсурдом, что я считаю, что ни один Человек, обладающий компетентной Способностью Мыслить в философских Вопросах, никогда не сможет впасть в него. Гравитация должна быть вызвана Агентом, действующим постоянно в соответствии с определенными законами; но является ли этот Агент материальным или нематериальным, я оставил на рассмотрение моих читателей. [1]
— Исаак Ньютон, Письма Бентли , 1692/3
Закон электрических сил Кулона изначально также был сформулирован как мгновенное действие на расстоянии, но в 1880 году Джеймс Клерк Максвелл показал, что уравнения поля , подчиняющиеся локальности, предсказывают все явления электромагнетизма. [ необходима цитата ] Эти уравнения показывают, что электромагнитные силы распространяются со скоростью света.
В 1905 году специальная теория относительности Альберта Эйнштейна постулировала , что никакая материя или энергия не может двигаться быстрее скорости света, и Эйнштейн таким образом стремился переформулировать физику таким образом, чтобы она подчинялась принципу локальности. Позднее ему удалось создать альтернативную теорию гравитации, общую теорию относительности , которая подчиняется принципу локальности.
Однако впоследствии другой вызов принципу локальности возник в теории квантовой механики , которую сам Эйнштейн помог создать.
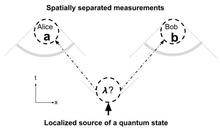
Простые пространственно-временные диаграммы могут помочь прояснить вопросы, связанные с локальностью. [2] Способ описания проблем локальности, подходящий для обсуждения квантовой механики, проиллюстрирован на диаграмме. Частица создается в одном месте, затем разделяется и измеряется в двух других, пространственно разделенных местах. Два измерения названы в честь Алисы и Боба. Алиса выполняет измерения (A) и получает результат ); Боб выполняет ( ) и получает результат . Эксперимент повторяется много раз, и результаты сравниваются.
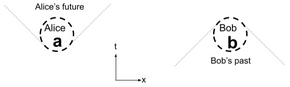
Пространственно-временная диаграмма имеет временную координату, идущую вертикально, и пространственную координату, идущую горизонтально. Алиса, в локальной области слева, может влиять на события только в конусе, простирающемся в будущее, как показано; конечная скорость света не позволяет ей влиять на другие области, включая местоположение Боба в этом случае. Аналогично мы можем использовать диаграмму, чтобы рассуждать о том, что локальные обстоятельства Боба не могут быть изменены Алисой в то же время: все события, которые оказывают влияние на Боба, находятся в конусе ниже его местоположения на диаграмме. Пунктирные линии вокруг Алисы показывают ее действительные будущие местоположения; пунктирные линии вокруг Боба показывают события, которые могли бы вызвать его текущие обстоятельства. Когда Алиса измеряет квантовые состояния в своем местоположении, она получает результаты, помеченные ; аналогично Боб получает . Модели локальности пытаются объяснить статистическую связь между этими измеренными значениями.
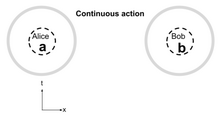
Простейшая модель локальности — это отсутствие локальности: мгновенное действие на расстоянии без ограничений для относительности. Модель локальности для действия на расстоянии называется непрерывным действием . [2] Серая область (здесь круг) — это математическое понятие, называемое «экраном». Любой путь из местоположения через экран становится частью физической модели в этом месте. Серое кольцо указывает, что события из всех частей пространства и времени могут влиять на вероятность, измеренную Алисой или Бобом. Таким образом, в случае непрерывного действия события во всех временах и местах влияют на модель Алисы и Боба. Эта простая модель весьма успешна для солнечной планетарной динамики с ньютоновской гравитацией и в электростатике, случаях, когда релятивистские эффекты незначительны.

Многие модели локальности явно или неявно игнорируют возможное влияние будущих событий. Пространственно-временная диаграмма справа показывает влияние такого ограничения в сочетании с непрерывным действием. Входные данные из будущего (выше пунктирной линии) больше не считаются частью модели Алисы или Боба. Сравнение этой диаграммы с диаграммой для непрерывного действия ясно показывает, что это не одна и та же модель локальности. [2] Аргументы здравого смысла о том, что будущее не влияет на настоящее, являются разумными критериями, но такие предположения изменяют математический характер моделей.

Джон Стюарт Белл при обсуждении своей теоремы Белла использует модель экранирования, показанную справа. События в общем прошлом Алисы и Боба являются частью модели, используемой при вычислении вероятностей для Алисы и Боба, как указано в способе, которым экран поглощает эти события. Однако события в местоположении Боба во время измерения Алисы и события в будущем исключаются. Белл назвал это предположение локальной причинностью , но с помощью диаграммы мы можем рассуждать о смысле предположения, не спотыкаясь о других значениях локального в сочетании с другими значениями причинного. [2] Пунктирные линии показывают релятивистски допустимые области в прошлом Алисы или Боба. Серая дуга — предполагаемый «экран» Белла.
Относительное положение наших немногих, легко различимых планет (например) можно увидеть напрямую: понимание и измерение их относительного расположения представляет собой только технические проблемы. С другой стороны, субмикроскопический мир известен только по измерениям, которые усредняют множество, казалось бы, случайных («статистических» или «вероятностных») событий, и измерения могут показывать либо корпускулярные, либо волнообразные результаты в зависимости от их конструкции. Этот мир управляется квантовой механикой . [3] Понятия локальности более сложны и описываются на языке вероятности и корреляции .
В статье о парадоксе Эйнштейна–Подольского–Розена (статья ЭПР) 1935 года [4] Альберт Эйнштейн , Борис Подольский и Натан Розен представили себе такой эксперимент. Они заметили, что квантовая механика предсказывает то, что сейчас известно как квантовая запутанность , и исследовали ее последствия. [5] По их мнению, классический принцип локальности подразумевал, что «никаких реальных изменений не может произойти» на месте Боба в результате любых измерений, которые проводила Алиса. Поскольку квантовая механика действительно предсказывает коллапс волновой функции , который зависит от выбора Бобом измерения, они пришли к выводу, что это была форма действия на расстоянии и что волновая функция не могла быть полным описанием реальности. Другие физики не согласились: они приняли квантовую волновую функцию как полную и подвергли сомнению природу локальности и реальности, предполагаемую в статье ЭПР. [6]
В 1964 году Джон Стюарт Белл исследовал, возможно ли достичь цели Эйнштейна — «завершить» квантовую теорию — с помощью локальных скрытых переменных , чтобы объяснить корреляции между пространственно разделенными частицами, как предсказывает квантовая теория. Белл установил критерий для различения теории локальных скрытых переменных и квантовой теории, измеряя определенные значения корреляций между запутанными частицами. Последующие экспериментальные тесты показали, что некоторые квантовые эффекты действительно нарушают неравенства Белла и не могут быть воспроизведены локальной теорией скрытых переменных. [5] Теорема Белла зависит от тщательно определенных моделей локальности.
Белл описал локальную причинность в терминах вероятности, необходимой для анализа квантовой механики. Используя обозначение, что для вероятности результата с заданным состоянием , Белл исследовал распределение вероятностей , где представляет собой набор скрытых переменных состояния (локально), когда две частицы изначально расположены совместно. Если локальная причинность сохраняется, то вероятности, наблюдаемые Алисой и Бобом, должны быть связаны только скрытыми переменными, и мы можем показать, что Белл доказал, что следствием этой факторизации являются ограничения на корреляции, наблюдаемые Алисой и Бобом, известные как неравенства Белла. Поскольку квантовая механика предсказывает корреляции, более сильные, чем этот предел, локально заданные скрытые переменные не могут быть добавлены к «полной» квантовой теории, как того требует статья ЭПР. [7]
Многочисленные эксперименты, специально разработанные для исследования проблем локальности, подтверждают предсказания квантовой механики; к ним относятся эксперименты, в которых два места измерения находятся на расстоянии более километра друг от друга. [7] [8] Нобелевская премия по физике 2022 года была присуждена Алену Аспекту , Джону Клаузеру и Антону Цайлингеру , в частности, «за эксперименты с запутанными фотонами, устанавливающие нарушение неравенств Белла». [9] Конкретный аспект квантовой теории, который приводит к этим корреляциям, называется квантовой запутанностью , и версии сценария Белла теперь используются для экспериментальной проверки запутанности. [7]
Математические результаты Белла, при сравнении с экспериментальными данными, исключают локальные скрытые переменные математических квантовых теорий. Но интерпретация математики по отношению к физическому миру остается предметом споров. Белл описал предположения, лежащие в основе его работы, как «локальную причинность», сокращенно «локальность»; более поздние авторы называли предположения локальным реализмом . [10] Эти различные названия не изменяют математические предположения.
Обзор статей [11], использующих эту фразу, показывает, что общее (классическое) физическое определение реализма — это
предположение, что результаты измерений четко определены до и независимо от измерений. [12]
Это определение включает в себя классические концепции, такие как «хорошо определенный», что противоречит квантовой суперпозиции , и «до ... измерений», что подразумевает (метафизическое) предсуществование свойств. В частности, термин локальный реализм в контексте теоремы Белла не может рассматриваться как разновидность «реализма», включающего локальность, отличную от той, которая подразумевается предположением экранирования Белла. Этот конфликт между общими идеями реализма и квантовой механики требует тщательного анализа всякий раз, когда обсуждается локальный реализм. [11] : 98 Добавление модификатора «локальности», что результаты двух пространственно хорошо разделенных измерений не могут причинно влиять друг на друга, [5] не делает комбинацию связанной с доказательством Белла; единственной интерпретацией, которую принял Белл, была та, которую он назвал локальной причинностью. [11] : 98 Следовательно, теорема Белла не ограничивает возможность нелокальных переменных, а также теорий, основанных на ретропричинности или супердетерминизме . [2]
Из-за вероятностной природы коллапса волновой функции это кажущееся нарушение локальности в квантовой механике не может быть использовано для передачи информации быстрее света, в соответствии с теоремой об отсутствии связи . [13] Эшер Перес различает слабую и сильную нелокальность , последняя относится к теориям, которые допускают связь быстрее света. В этих условиях квантовая механика допускает слабо нелокальные корреляции, но не сильную нелокальность. [14]
Одним из основных принципов квантовой теории поля является принцип локальности. [15] Операторы поля и плотность лагранжиана, описывающие динамику полей, являются локальными в том смысле, что взаимодействия не описываются действием на расстоянии. Этого можно достичь, избегая членов в лагранжиане, которые являются произведениями двух полей, зависящих от удаленных координат. [15] [16] В частности, в релятивистской квантовой теории поля для обеспечения принципов локальности и причинности требуется следующее условие: если есть две наблюдаемые , каждая из которых локализована в двух различных областях пространства-времени, которые случайно оказываются на пространственноподобном расстоянии друг от друга, наблюдаемые должны коммутировать . Это условие иногда навязывается как одна из аксиом релятивистской квантовой теории поля. [15] [17]