Проблема с днем рождения

В теории вероятностей задача о днях рождения требует вероятности того, что среди $n$ случайно выбранных людей по крайней мере двое будут иметь один и тот же день рождения . Парадокс дней рождения относится к контринтуитивному факту, что для того, чтобы эта вероятность превысила 50%, нужно всего 23 человека.

Парадокс дней рождения — это истинный парадокс : на первый взгляд он кажется неверным, но на самом деле это правда. Хотя может показаться удивительным, что для достижения 50% вероятности общего дня рождения требуется всего 23 человека, этот результат становится более интуитивным, если учесть, что сравнения дней рождения будут проводиться между каждой возможной парой людей. При 23 людях есть ⁠23 × 22/2⁠ = 253 пары для рассмотрения, что намного больше половины количества дней в году.

Реальные приложения для проблемы дней рождения включают криптографическую атаку, называемую атакой дней рождения , которая использует эту вероятностную модель для уменьшения сложности поиска коллизии для хэш-функции , а также для вычисления приблизительного риска коллизии хэшей, существующей в хэшах заданного размера популяции.

Эту задачу обычно приписывают Гарольду Дэвенпорту примерно в 1927 году, хотя он не опубликовал ее в то время. Дэвенпорт не утверждал, что является ее первооткрывателем, «потому что не мог поверить, что она не была сформулирована ранее». ^[1]^[2] Первая публикация версии задачи о днях рождения была сделана Рихардом фон Мизесом в 1939 году. ^[3]

Расчет вероятности

С точки зрения перестановок , пусть событие $A$ будет вероятностью нахождения группы из 23 человек без повторяющихся дней рождения. Где событие $B$ является вероятностью нахождения группы из 23 человек, в которой по крайней мере двое людей имеют одинаковый день рождения, $P (B) = 1 - P (A)$ . $P (A)$ является отношением общего количества дней рождения, , без повторений и порядка (например, для группы из 2 человек, формат дня рождения мм/дд, один возможный результат ), деленным на общее количество дней рождения с повторением и порядком, , поскольку это общее пространство результатов эксперимента (например, 2 человека, один возможный результат ). Следовательно , и являются перестановками . $V_{номер}$ $\left\{\left\{01/02,05/20\right\},\left\{05/20,01/02\right\},\left\{10/02,08/04\right\},...\right\}$ $V_{т}$ $\left\{\left\{01/02,01/02\right\},\left\{10/02,08/04\right\},...\right\}$ $V_{номер}$ $V_{т}$

{\begin{aligned}V_{nr}&={\frac {n!}{(nk)!}}={\frac {365!}{(365-23)!}}\\[8pt]V_{t}&=n^{k}=365^{23}\\[8pt]P(A)&={\frac {V_{nr}}{V_{t}}}\приблизительно 0,492703\\[8pt]P(B)&=1-P(A)\приблизительно 1-0,492703\приблизительно 0,507297\quad (50,7297\%)\end{aligned}}

Другой способ решения проблемы дней рождения — запросить приблизительную вероятность того, что в группе из $n$ человек по крайней мере двое имеют одинаковый день рождения. Для простоты високосные годы , близнецы , смещение отбора и сезонные и недельные колебания рождаемости ^[4] обычно игнорируются, и вместо этого предполагается, что существует 365 возможных дней рождения, и что день рождения каждого человека с равной вероятностью может приходиться на любой из этих дней, независимо от других людей в группе.

Для независимых дней рождения равномерное распределение дней рождения минимизирует вероятность того, что у двух людей в группе будет одинаковый день рождения. Любая неравномерность увеличивает вероятность того, что у двух людей будет один и тот же день рождения. ^[5]^[6] Однако в реальном мире дни рождения недостаточно неравномерны, чтобы внести существенные изменения: размер реальной группы, необходимый для того, чтобы вероятность общего дня рождения была больше 50%, составляет 23, как и в теоретическом равномерном распределении. ^[7]

Цель состоит в том, чтобы вычислить $P (B)$ , вероятность того, что по крайней мере два человека в комнате имеют одинаковый день рождения. Однако проще вычислить $P (A')$ , вероятность того, что ни у одного из двух людей в комнате нет одинакового дня рождения. Тогда, поскольку $B$ и $A'$ являются единственными двумя возможностями, и они также являются взаимоисключающими , $P (B) = 1 - P (A').$

Вот расчет $P (B)$ для 23 человек. Пусть 23 человека будут пронумерованы от 1 до 23. Событие , что все 23 человека имеют разные дни рождения, то же самое, что и событие, что человек 2 не имеет тот же день рождения, что и человек 1, и что человек 3 не имеет тот же день рождения, что и человек 1 или человек 2, и так далее, и, наконец, что человек 23 не имеет тот же день рождения, что и любой из людей от 1 до 22. Пусть эти события будут называться Событием 2, Событием 3 и так далее. Событием 1 является событие, что человек 1 имеет день рождения, что происходит с вероятностью 1. Это сочетание событий может быть вычислено с использованием условной вероятности : вероятность События 2 равна ⁠364/365⁠ , поскольку у человека 2 может быть любой день рождения, кроме дня рождения человека 1. Аналогично, вероятность События 3 при условии, что произошло Событие 2, равна ⁠363/365⁠ , поскольку у человека 3 может быть любой из дней рождения, еще не отмечаемых людьми 1 и 2. Это продолжается до тех пор, пока, наконец, вероятность события 23, учитывая, что все предыдущие события произошли, не составит ⁠343/365⁠ . Наконец, принцип условной вероятности подразумевает, что $P (A')$ равно произведению этих индивидуальных вероятностей:

Члены уравнения ( 1 ) можно объединить, чтобы получить:

Оценка уравнения ( 2 ) дает $P (A') \approx 0,492703$

Следовательно, $P (B) \approx 1 - 0,492703 = 0,507297$ (50,7297%).

Этот процесс можно обобщить на группу из $n$ человек, где $p (n)$ — вероятность того, что хотя бы двое из $n$ человек имеют одинаковый день рождения. Сначала проще вычислить вероятность $p (n)$ того, что все $n$ дней рождения различны . Согласно принципу ящика , $p (n)$ равно нулю, когда $n > 365.$ Когда $n \leq 365$ :

{\begin{aligned}{\bar {p}}(n)&=1\times \left(1-{\frac {1}{365}}\right)\times \left(1-{\frac {2}{365}}\right)\times \cdots \times \left(1-{\frac {n-1}{365}}\right)\\[6pt]&={\frac {365\times 364\times \cdots \times (365-n+1)}{365^{n}}}\\[6pt]&={\frac {365!}{365^{n}(365-n)!}}={\frac {n!\cdot {\binom {365}{n}}}{365^{n}}}={\frac {_{365}P_{n}}{365^{n}}}\end{align}}

где $!$ — оператор факториала , $(365 н.)$ — биномиальный коэффициент , а $k P r$ обозначает перестановку .

Уравнение выражает тот факт, что у первого человека нет никого, с кем можно было бы разделить день рождения, у второго человека не может быть того же дня рождения, что и у первого $(⁠ 364 / 365 ⁠)$ , третий не может иметь тот же день рождения, что и любой из первых двух $(⁠ 363 / 365 ⁠)$ , и в общем случае $n$ -й день рождения не может совпадать ни с одним из $n - 1$ предыдущих дней рождения.

Событие , что хотя бы двое из $n$ человек имеют одинаковый день рождения, является дополнительным к тому, что все $n$ дней рождения различны. Поэтому его вероятность $p (n)$ равна

p(n)=1-{\bar {p}}(n).

В следующей таблице показана вероятность некоторых других значений $n$ (в этой таблице существование високосных лет игнорируется, и предполагается, что каждый день рождения имеет одинаковую вероятность):

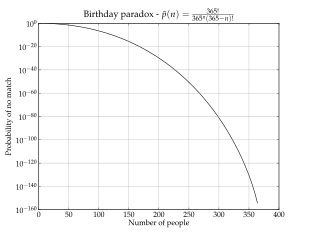
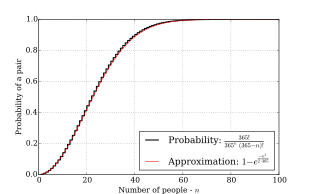
Вероятность того, что в группе из $n$ человек нет двух людей с одинаковым днем рождения. Обратите внимание, что вертикальная шкала логарифмическая (каждый шаг вниз в 10 ²⁰ раз меньше вероятности).

Приближения

Разложение показательной функции в ряд Тейлора ( константа $e$ $\approx$ $2.718 281828$ )

e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots

обеспечивает приближение первого порядка для $e x$ для : $|x|\ll 1$

e^{x}\approx 1+x.

Чтобы применить это приближение к первому выражению, полученному для $p (n)$ , положим $x = - ⁠ а / 365 ⁠$ . Таким образом,

e^{-a/365}\approx 1-{\frac {a}{365}}.

Затем замените $a$ неотрицательными целыми числами для каждого члена в формуле $p (n)$ до тех пор, пока $a = n - 1$ , например, когда $a = 1$ ,

e^{-1/365}\approx 1-{\frac {1}{365}}.

Первое выражение, полученное для $p (n),$ можно аппроксимировать как

{\begin{aligned}{\bar {p}}(n)&\approx 1\cdot e^{-1/365}\cdot e^{-2/365}\cdots e^{-(n-1)/365}\\[6pt]&=e^{-{\big (}1+2+\,\cdots \,+(n-1){\big )}/365}\\[6pt]&=e^{-{\frac {n(n-1)/2}{365}}}=e^{-{\frac {n(n-1)}{730}}}.\end{aligned}}

Поэтому,

p(n)=1-{\bar {p}}(n)\approx 1-e^{-{\frac {n(n-1)}{730}}}.

Еще более грубое приближение дается выражением

p(n)\approx 1-e^{-{\frac {n^{2}}{730}}},

что, как показывает график, по-прежнему довольно точно.

Согласно приближению, тот же подход может быть применен к любому количеству "людей" и "дней". Если вместо 365 дней есть $d$ , если есть $n$ человек, и если $n ≪ d$ , то используя тот же подход, что и выше, мы достигаем результата, что если $p (n, d)$ - это вероятность того, что по крайней мере двое из $n$ людей разделяют один и тот же день рождения из набора из $d$ доступных дней, то:

{\begin{aligned}p(n,d)&\approx 1-e^{-{\frac {n(n-1)}{2d}}}\\[6pt]&\approx 1-e^{-{\frac {n^{2}}{2d}}}.\end{aligned}}

Простое возведение в степень

Вероятность того, что у двух людей не совпадут дни рождения, равна ⁠364/365⁠ . В комнате, содержащей n человек, находятся $(н 2) = ⁠ н (н - 1) / 2 ⁠$ пары людей, т.е. $(н 2)$ событий. Вероятность того, что у двух людей не будет одинаковых дней рождения, можно приблизительно оценить, предположив, что эти события независимы, и, следовательно, перемножив их вероятности. Быть независимым было бы эквивалентно выбору с заменой любой пары людей в мире, а не только в комнате. Короче говоря ⁠364/365⁠ можно умножить на себя $(н 2)$ раз, что дает нам

{\bar {p}}(n)\approx \left({\frac {364}{365}}\right)^{\binom {n}{2}}.

Поскольку это вероятность того, что ни у кого нет одинакового дня рождения, то вероятность того, что у кого-то будет одинаковый день рождения, равна

p(n)\approx 1-\left({\frac {364}{365}}\right)^{\binom {n}{2}}.

А для группы из 23 человек вероятность обмена составляет

p(23)\approx 1-\left({\frac {364}{365}}\right)^{\binom {23}{2}}=1-\left({\frac {364}{365}}\right)^{253}\approx 0.500477.

приближение Пуассона

Применив приближение Пуассона для биномиального распределения к группе из 23 человек,

\operatorname {Poi} \left({\frac {\binom {23}{2}}{365}}\right)=\operatorname {Poi} \left({\frac {253}{365}}\right)\approx \operatorname {Poi} (0.6932)

так

\Pr(X>0)=1-\Pr(X=0)\approx 1-e^{-0.6932}\approx 1-0.499998=0.500002.

Результат составляет более 50% от предыдущих описаний. Это приближение такое же, как и приведенное выше, основанное на разложении Тейлора, которое использует $e x \approx 1 + x$ .

Квадратное приближение

Хорошим практическим правилом , которое можно использовать для устных вычислений, является соотношение

p(n,d)\approx {\frac {n^{2}}{2d}}

что также можно записать как

n\approx {\sqrt {2d\times p(n)}}

что хорошо работает для вероятностей, меньших или равных ⁠1/2⁠ . В этих уравнениях $d$ — количество дней в году.

Например, чтобы оценить количество людей, необходимых для ⁠1/2⁠ шанс на общий день рождения, мы получаем

n\approx {\sqrt {2\times 365\times {\tfrac {1}{2}}}}={\sqrt {365}}\approx 19

Что не так уж далеко от правильного ответа — 23.

Приблизительное количество людей

Это также можно приблизительно рассчитать, используя следующую формулу для количества людей, необходимых для того, чтобы иметь по крайней мере ⁠1/2⁠ вероятность совпадения:

n\geq {\tfrac {1}{2}}+{\sqrt {{\tfrac {1}{4}}+2\times \ln(2)\times 365}}=22.999943.

Это результат хорошего приближения, что событие с $⁠$ $1 / к ⁠$ вероятность будет иметь ⁠1/2⁠ вероятность появления хотя бы один раз, если оно повторяется $k ln 2$ раз. ^[8]

Таблица вероятностей

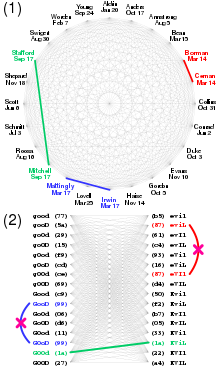
Более светлые поля в этой таблице показывают количество хэшей, необходимых для достижения заданной вероятности коллизии (столбец) при заданном хэш-пространстве определенного размера в битах (строка). Используя аналогию с днем рождения: «размер хэш-пространства» напоминает «доступные дни», «вероятность коллизии» напоминает «вероятность общего дня рождения», а «требуемое количество хэшированных элементов» напоминает «требуемое количество людей в группе». Эту таблицу также можно использовать для определения минимально необходимого размера хэша (при заданных верхних границах хэшей и вероятности ошибки) или вероятности коллизии (для фиксированного количества хэшей и вероятности ошибки).

Для сравнения,10 ⁻¹⁸ в10 ⁻¹⁵ — это неисправимая частота ошибок битов типичного жесткого диска. ^[9] Теоретически, 128-битные хэш-функции, такие как MD5 , должны оставаться в этом диапазоне до тех пор, пока8,2 × 1011 ^{документов} , даже если возможных выходных данных гораздо больше.

Верхняя граница вероятности и нижняя граница количества людей

Приведенный ниже аргумент взят из аргумента Пола Халмоса . ^{[nb 1]}

Как указано выше, вероятность того, что ни один из двух дней рождения не совпадет, равна

1-p(n)={\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right).

Как и в предыдущих параграфах, интерес представляет наименьшее $n,$ такое, что $p (n) > ⁠ 1 / 2 ⁠$ ; или, что эквивалентно, наименьшее $n$ такое, что $p (n) < ⁠ 1 / 2 ⁠$ .

Используя неравенство $1 - x < e - x$ в приведенном выше выражении, заменяем $1 - ⁠ к / 365 ⁠$ с $e .mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}− k ⁄ 365.$ Это дает

{\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right)<\prod _{k=1}^{n-1}\left(e^{-{\frac {k}{365}}}\right)=e^{-{\frac {n(n-1)}{730}}}.

Следовательно, выражение выше является не только приближением, но и верхней границей p $(n) .$ Неравенство

e^{-{\frac {n(n-1)}{730}}}<{\frac {1}{2}}

подразумевает $p (n) < ⁠ 1 / 2 ⁠$ . Решение для $n$ дает

n^{2}-n>730\ln 2.

Теперь $730 ln 2$ приблизительно равно 505,997, что немного меньше 506, значения $n 2 - n,$ достигаемого при $n = 23.$ Следовательно, достаточно 23 человек. Кстати, решение $n 2 - n = 730 ln 2$ относительно n дает приближенную формулу Фрэнка Х. Матиса, цитированную выше.

Этот вывод показывает только то, что для обеспечения как минимум равных шансов совпадения дней рождения необходимо не более 23 человек; он оставляет открытой возможность, что $n$ равно 22 или меньше, что также может сработать.

Обобщения

Произвольное количество дней

Если год состоит из $d$ дней, обобщенная задача о днях рождения требует минимального числа $n (d),$ такого, что в наборе из $n$ случайно выбранных людей вероятность совпадения дней рождения составляет не менее 50%. Другими словами, $n (d)$ — это минимальное целое число $n,$ такое, что

1-\left(1-{\frac {1}{d}}\right)\left(1-{\frac {2}{d}}\right)\cdots \left(1-{\frac {n-1}{d}}\right)\geq {\frac {1}{2}}.

Классическая проблема дня рождения, таким образом, соответствует определению $n (365)$ . Первые 99 значений $n (d)$ приведены здесь (последовательность A033810 в OEIS ):

Аналогичный расчет показывает, что $n (d)$ = 23, когда $d$ находится в диапазоне 341–372.

Было опубликовано множество оценок и формул для $n (d) .$ ^[10] Для любого $d \geq 1$ число $n (d)$ удовлетворяет ^[11]

{\frac {3-2\ln 2}{6}}<n(d)-{\sqrt {2d\ln 2}}\leq 9-{\sqrt {86\ln 2}}.

Эти границы оптимальны в том смысле, что последовательность $n (d) - \sqrt 2 d ln 2$ становится произвольно близкой к

{\frac {3-2\ln 2}{6}}\approx 0.27,

в то время как он имеет

9-{\sqrt {86\ln 2}}\approx 1.28

в качестве максимума принимается $d = 43$ .

Границы достаточно узкие, чтобы дать точное значение $n (d)$ в большинстве случаев. Например, для $d =$ 365 эти границы подразумевают, что $22,7633 < n (365) < 23,7736$ и 23 — единственное целое число в этом диапазоне. В общем, из этих границ следует, что $n (d)$ всегда равно либо

\left\lceil {\sqrt {2d\ln 2}}\,\right\rceil \quad {\text{or}}\quad \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil +1

где $⌈ \cdot ⌉$ обозначает функцию потолка . Формула

n(d)=\left\lceil {\sqrt {2d\ln 2}}\,\right\rceil

справедлива для 73% всех целых чисел $d$ . ^[12] Формула

n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}\right\rceil

справедливо для почти всех $d$ , т.е. для набора целых чисел $d$ с асимптотической плотностью 1. ^[12]

Формула

n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}\right\rceil

справедливо для всех $d \leq 1018$ , но предполагается, что существует бесконечно много контрпримеров к этой формуле.^[13]

Формула

n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}-{\frac {2(\ln 2)^{2}}{135d}}\right\rceil

справедливо для всех $d \leq 1018$ , и предполагается, что эта формула верна для всех $d$ .^[13]

Более двух человек имеют один и тот же день рождения

Можно расширить задачу, спросив, сколько человек должно быть в группе, чтобы вероятность того, что по крайней мере 3, 4, 5 и т. д. человек из группы имеют одинаковый день рождения, превышала 50%.

Первые несколько значений следующие: >50% вероятности того, что у 3 человек будет один и тот же день рождения — 88 человек; >50% вероятности того, что у 4 человек будет один и тот же день рождения — 187 человек (последовательность A014088 в OEIS ). ^[14]

Вероятность совпадения дней рождения (столкновение)

Задачу о днях рождения можно обобщить следующим образом:

Дано

n

случайных целых чисел, взятых из дискретного равномерного распределения с диапазоном

[1, d]

, какова вероятность

p (n; d)

того, что по крайней мере два числа будут одинаковыми? (

d = 365

дает обычную задачу о днях рождения.) ^[15]

Общие результаты можно получить, используя те же аргументы, что и приведенные выше.

{\begin{aligned}p(n;d)&={\begin{cases}1-\displaystyle \prod _{k=1}^{n-1}\left(1-{\frac {k}{d}}\right)&n\leq d\\1&n>d\end{cases}}\\[8px]&\approx 1-e^{-{\frac {n(n-1)}{2d}}}\\&\approx 1-\left({\frac {d-1}{d}}\right)^{\frac {n(n-1)}{2}}\end{aligned}}

И наоборот, если $n (p; d)$ обозначает количество случайных целых чисел, взятых из $[1, d]$ , чтобы получить вероятность $p$ того, что по крайней мере два числа одинаковы, то

n(p;d)\approx {\sqrt {2d\cdot \ln \left({\frac {1}{1-p}}\right)}}.

Проблема дней рождения в этом более общем смысле применима к хэш-функциям : ожидаемое число $N$ - битных хешей, которые могут быть сгенерированы до возникновения коллизии, составляет не $2 N$ , а всего лишь $2 N ⁄ 2.$ Это используется в атаках на дни рождения криптографических хэш-функций и является причиной того, что небольшое число коллизий в хэш-таблице неизбежно для всех практических целей.

Теория, лежащая в основе проблемы дней рождения, была использована Зои Шнабель ^[16] под названием «статистика повторного улова» для оценки численности популяции рыб в озерах.

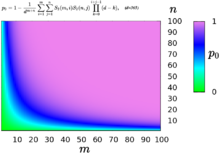
Обобщение на несколько типов людей

Основная проблема рассматривает все испытания как относящиеся к одному «типу». Проблема дней рождения была обобщена для рассмотрения произвольного числа типов. ^[17] В простейшем расширении есть два типа людей, скажем, $m$ мужчин и $n$ женщин, и проблема становится характеристикой вероятности общего дня рождения по крайней мере у одного мужчины и одной женщины. (Общие дни рождения у двух мужчин или двух женщин не учитываются.) Вероятность отсутствия общих дней рождения здесь равна

p_{0}={\frac {1}{d^{m+n}}}\sum _{i=1}^{m}\sum _{j=1}^{n}S_{2}(m,i)S_{2}(n,j)\prod _{k=0}^{i+j-1}d-k

где $d = 365$ и $S 2$ — числа Стирлинга второго рода . Следовательно, искомая вероятность равна $1 - p 0$ .

Эта вариация задачи о днях рождения интересна тем, что не существует единственного решения для общего числа людей $m + n$ . Например, обычное значение вероятности 50% реализуется как для группы из 32 человек из 16 мужчин и 16 женщин, так и для группы из 49 человек из 43 женщин и 6 мужчин.

Другие проблемы с днем рождения

Первый матч

Смежный вопрос: когда люди входят в комнату по одному, кто из них, скорее всего, будет первым, у кого будет тот же день рождения, что и у кого-то, уже находящегося в комнате? То есть, для какого $n максимально$ $p (n) - p (n - 1)$ ? Ответ 20 — если есть приз за первое совпадение, то лучшая позиция в очереди — 20-я. ^{[ требуется цитата ]}

Тот же день рождения, что и у тебя

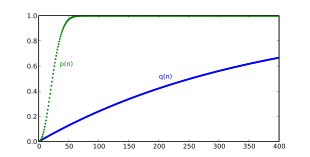
В задаче о днях рождения ни один из двух людей не выбран заранее. Напротив, вероятность $q (n)$ того, что по крайней мере один другой человек в комнате из $n$ других людей имеет тот же день рождения, что и конкретный человек (например, вы), задается как

q(n)=1-\left({\frac {365-1}{365}}\right)^{n}

и для общего $d$ по

q(n;d)=1-\left({\frac {d-1}{d}}\right)^{n}.

В стандартном случае $d = 365$ подстановка $n = 23$ дает около 6,1%, что меньше 1 шанса из 16. Для более чем 50% вероятности того, что хотя бы у одного человека в комнате, полной $n$ человек, день рождения совпадает с вашим , $n$ должно быть не менее 253. Это число значительно больше, чем $⁠$ $365 / 2 ⁠ = 182,5$ : причина в том, что, скорее всего, у некоторых людей в комнате совпадают дни рождения.

Количество людей с общим днем рождения

Для любого человека в группе из n человек вероятность того, что он или она разделит свой день рождения с кем-то еще, равна , как объяснено выше. Ожидаемое количество людей с общим (не уникальным) днем рождения теперь можно легко вычислить, умножив эту вероятность на количество людей ( n ), так что это: $q(n-1;d)$

n\left(1-\left({\frac {d-1}{d}}\right)^{n-1}\right)

(Это умножение можно выполнить таким образом из-за линейности ожидаемого значения переменных-индикаторов). Это означает, что ожидаемое число людей с несовпадающим (уникальным) днем рождения равно:

n\left({\frac {d-1}{d}}\right)^{n-1}

Аналогичные формулы можно вывести для ожидаемого числа людей, которые делят комнату с тремя, четырьмя и т. д. другими людьми.

Количество людей до наступления каждого дня рождения

Ожидаемое количество людей, необходимое для достижения каждого дня рождения, называется задачей коллекционера купонов . Ее можно рассчитать по формуле $nH n$ , где $H n$ — $n$ -ое гармоническое число . Для 365 возможных дат (задача о днях рождения) ответ — 2365.

Рядом с совпадениями

Другое обобщение — спросить о вероятности нахождения хотя бы одной пары в группе из $n$ человек с днями рождения в пределах $k$ календарных дней друг от друга, если имеется $d$ равновероятных дней рождения. ^[18]

{\begin{aligned}p(n,k,d)&=1-{\frac {(d-nk-1)!}{d^{n-1}{\bigl (}d-n(k+1){\bigr )}!}}\end{aligned}}

Число людей, необходимое для того, чтобы вероятность того, что у какой-то пары дни рождения будут разделены $k$ днями или меньше, была выше 50%, указано в следующей таблице:

Таким образом, в группе из семи случайных людей, скорее всего, у двоих из них будет день рождения с разницей в неделю. ^[18]

Количество дней с определенным количеством дней рождения

Количество дней, в течение которых отмечается хотя бы один день рождения

Ожидаемое количество разных дней рождения, т.е. количество дней, которые являются днем рождения хотя бы одного человека, составляет:

d-d\left({\frac {d-1}{d}}\right)^{n}

Это следует из ожидаемого количества дней, в течение которых у кого-либо не будет дня рождения:

d\left({\frac {d-1}{d}}\right)^{n}

что следует из вероятности того, что в определенный день не будет чьего-либо дня рождения, $(⁠ д - 1 / г ⁠) н$ , легко суммируется из-за линейности ожидаемого значения.

Например, при $d = 365$ следует ожидать около 21 разных дней рождения, когда есть 22 человека, или 46 разных дней рождения, когда есть 50 человек. Когда есть 1000 человек, будет около 341 разных дней рождения (24 невостребованных дня рождения).

Количество дней, в которые приходится не менее двух дней рождения

Вышеизложенное можно обобщить на основе распределения числа людей, чей день рождения приходится на любой конкретный день, которое представляет собой биномиальное распределение с вероятностью $⁠$ $1 / г ⁠$ . Умножение соответствующей вероятности на $d$ даст ожидаемое количество дней. Например, ожидаемое количество дней, которые являются общими; т. е. которые являются по крайней мере двумя (т. е. не нулем и не одним) днями рождения людей, составляет:

$d-d\left({\frac {d-1}{d}}\right)^{n}-d\cdot {\binom {n}{1}}\left({\frac {1}{d}}\right)^{1}\left({\frac {d-1}{d}}\right)^{n-1}=d-d\left({\frac {d-1}{d}}\right)^{n}-n\left({\frac {d-1}{d}}\right)^{n-1}$

Количество людей, которые повторяют день рождения

Вероятность того, что $k$ -е целое число, случайно выбранное из $[1, d]$ , повторит хотя бы один предыдущий выбор, равна $q (k - 1; d)$ выше. Ожидаемое общее количество раз, когда выбор повторит предыдущий выбор, когда выбрано $n таких целых чисел, равно$ ^[19]

\sum _{k=1}^{n}q(k-1;d)=n-d+d\left({\frac {d-1}{d}}\right)^{n}

Можно увидеть, что это равно количеству людей за вычетом ожидаемого количества различных дней рождения.

Среднее количество людей, у которых хотя бы один день рождения совпал

В альтернативной формулировке задачи о днях рождения задается среднее число людей, необходимое для нахождения пары с одинаковым днем рождения. Если мы рассмотрим функцию вероятности Pr[ $n$ людей имеют по крайней мере один общий день рождения], это среднее значение определяет среднее значение распределения, в отличие от обычной формулировки, которая запрашивает медиану . Задача имеет отношение к нескольким алгоритмам хеширования, проанализированным Дональдом Кнутом в его книге «Искусство программирования» . Можно показать ^[20]^[21] , что если сделать выборку равномерно, с заменой, из популяции размером $M$ , то число попыток, необходимых для первой повторной выборки некоторого человека, имеет ожидаемое значение $n = 1 + Q (M)$ , где

Q(M)=\sum _{k=1}^{M}{\frac {M!}{(M-k)!M^{k}}}.

Функция

Q(M)=1+{\frac {M-1}{M}}+{\frac {(M-1)(M-2)}{M^{2}}}+\cdots +{\frac {(M-1)(M-2)\cdots 1}{M^{M-1}}}

был изучен Шринивасой Рамануджаном и имеет асимптотическое разложение :

Q(M)\sim {\sqrt {\frac {\pi M}{2}}}-{\frac {1}{3}}+{\frac {1}{12}}{\sqrt {\frac {\pi }{2M}}}-{\frac {4}{135M}}+\cdots .

При $M = 365$ дней в году среднее количество людей, необходимое для нахождения пары с одинаковым днем рождения, равно $n = 1 + Q (M) \approx 24,61659$ , что немного больше 23, числа, необходимого для 50% вероятности. В лучшем случае хватит двух человек; в худшем случае потребуется максимально возможное количество $M + 1 = 366$ человек; но в среднем требуется всего 25 человек

Анализ с использованием индикаторных случайных величин может обеспечить более простой, но приблизительный анализ этой проблемы. ^[22] Для каждой пары ( i , j ) для k человек в комнате мы определяем индикаторную случайную величину X _ij , для , как $1\leq i\leq j\leq k$

${\begin{alignedat}{2}X_{ij}&=I\{{\text{person }}i{\text{ and person }}j{\text{ have the same birthday}}\}\\[10pt]&={\begin{cases}1,&{\text{if person }}i{\text{ and person }}j{\text{ have the same birthday;}}\\0,&{\text{otherwise.}}\end{cases}}\end{alignedat}}$

${\begin{alignedat}{2}E[X_{ij}]&=\Pr\{{\text{person }}i{\text{ and person }}j{\text{ have the same birthday}}\}={\frac {1}{n}}.\end{alignedat}}$

Пусть X — случайная величина, подсчитывающая пары людей с одинаковым днем рождения.

$X=\sum _{i=1}^{k}\sum _{j=i+1}^{k}X_{ij}$

${\begin{alignedat}{3}E[X]&=\sum _{i=1}^{k}\sum _{j=i+1}^{k}E[X_{ij}]\\[8pt]&={\binom {k}{2}}{\frac {1}{n}}\\[8pt]&={\frac {k(k-1)}{2n}}\end{alignedat}}$

Для $n = 365$ , если $k = 28$ , ожидаемое число пар людей с одинаковым днем рождения равно ⁠28 × 27/2 × 365⁠ ≈ 1,0356. Таким образом, мы можем ожидать по крайней мере одну совпадающую пару с по крайней мере 28 людьми.

На чемпионате мира по футболу FIFA 2014 года в каждой из 32 команд было по 23 игрока. Анализ официальных списков команд показал, что в 16 командах были пары игроков с одинаковыми днями рождения, и из этих 5 команд было по две пары: в Аргентине, Франции, Иране, Южной Корее и Швейцарии было по две пары, а в Австралии, Боснии и Герцеговине, Бразилии, Камеруне, Колумбии, Гондурасе, Нидерландах, Нигерии, России, Испании и США — по одной паре. ^[23]

Ворачек, Тран и Форман показали, что большинство людей заметно переоценивают количество людей, необходимое для достижения заданной вероятности того, что у людей одинаковый день рождения, и заметно недооценивают вероятность того, что у людей одинаковый день рождения, когда задан определенный размер выборки. ^[24] Дальнейшие результаты показали, что студенты-психологи и женщины справились с заданием лучше, чем посетители/персонал казино или мужчины, но были менее уверены в своих оценках.

Обратная задача

Обратная задача состоит в том, чтобы для фиксированной вероятности $p$ найти наибольшее $n$ , для которого вероятность $p (n)$ меньше заданного $p$ , или наименьшее $n$ , для которого вероятность $p (n)$ больше заданного $p$ . ^{[ необходима ссылка ]}

Принимая вышеприведенную формулу для $d = 365$ , имеем

n(p;365)\approx {\sqrt {730\ln \left({\frac {1}{1-p}}\right)}}.

В следующей таблице приведены некоторые примеры расчетов.

Некоторые значения, выходящие за пределы допустимых значений, выделены цветом, чтобы показать, что приближение не всегда является точным.

Проблема с разделом

Связанная проблема — проблема разделения , вариант задачи о рюкзаке из исследования операций . На весы кладут несколько гирь ; каждая гиря — это целое число граммов, случайно выбранное в диапазоне от одного грамма до одного миллиона граммов (одна тонна ). Вопрос в том, можно ли обычно (то есть с вероятностью, близкой к 1) перекладывать гири между левым и правым плечами, чтобы уравновесить весы. (В случае, если сумма всех гирь составляет нечетное число граммов, допускается расхождение в один грамм.) Если есть только две или три гири, ответ совершенно очевиден: нет; хотя есть некоторые комбинации, которые работают, большинство случайно выбранных комбинаций из трех гирь не работают. Если гирь очень много, ответ совершенно очевиден: да. Вопрос в том, сколько их будет достаточно? То есть, каково количество гирь, чтобы с одинаковой вероятностью можно было уравновесить их и невозможно?

Часто интуиция подсказывает людям, что ответ находится выше.100 000. Большинство людей интуитивно чувствуют, что это тысячи или десятки тысяч, в то время как другие чувствуют, что это должно быть, по крайней мере, сотни. Правильный ответ - 23. ^{[ необходима цитата ]}

Причина в том, что правильное сравнение — это количество разделов весов на левое и правое. Существует $2 N - 1$ различных разделов для $N$ весов, и левая сумма минус правая сумма может рассматриваться как новая случайная величина для каждого раздела. Распределение суммы весов приблизительно гауссово , с пиком при $500000 Н$ и ширина $1000000 \sqrt N$ , так что когда $2 N - 1$ приблизительно равно $1000000 \sqrt N$ происходит переход. 2^{23 − 1} составляет около 4 миллионов, тогда как ширина распределения составляет всего 5 миллионов.^[25]

В художественной литературе

Роман Артура Кларка 1961 года «Падение лунной пыли» содержит раздел, в котором главные герои, запертые под землей на неопределенное время, празднуют день рождения и обсуждают справедливость проблемы дней рождения. Как сказал пассажир-физик: «Если у вас группа из более чем двадцати четырех человек, то вероятность того, что у двоих из них будет один и тот же день рождения, выше, чем даже у двоих». В конце концов, из 22 присутствующих выясняется, что у двух персонажей один и тот же день рождения — 23 мая.

Примечания

^ В своей автобиографии Халмош критиковал форму, в которой часто представляется парадокс дня рождения, в терминах численных вычислений. Он считал, что его следует использовать в качестве примера при использовании более абстрактных математических концепций. Он писал:
Рассуждения основаны на важных инструментах, к которым все студенты-математики должны иметь свободный доступ. Задача о дне рождения была прекрасной иллюстрацией преимуществ чистого мышления над механическими манипуляциями; неравенства можно получить за минуту или две, тогда как умножение заняло бы гораздо больше времени и было бы гораздо более подвержено ошибкам, будь то инструмент — карандаш или старомодный настольный компьютер. Чего не дают калькуляторы, так это понимания, или математической ловкости, или прочной основы для более продвинутых, обобщенных теорий.

Ссылки

^ Дэвид Сингмастер , Источники по занимательной математике: аннотированная библиография , восьмое предварительное издание, 2004, раздел 8.B
^ HSM Coxeter , «Математические развлечения и эссе», 11-е издание, 1940, стр. 45, как сообщается в IJ Good , Вероятность и взвешивание доказательств , 1950, стр. 38
^ Ричард фон Мизес, «Über Aufteilungs- und Besetzungswahrscheinlichkeiten», Revue de la Faculté des Sciences de l'Université d'Istanbul 4 : 145-163, 1939, перепечатано в Frank, P.; Гольдштейн, С.; Кац, М.; Прагер, В.; Сегё, Г.; Биркгоф, Г., ред. (1964). Избранные статьи Рихарда фон Мизеса . Том. 2. Провиденс, Род-Айленд: Амер. Математика. Соц. стр. 313–334.
^ см . Распределение дней рождения по году
^ (Блум 1973)
^ Стил, Дж. Майкл (2004). Мастер-класс Коши-Шварца . Кембридж: Издательство Кембриджского университета. С. 206, 277. ISBN 9780521546775.
^ Марио Кортина Борха; Джон Хейг (сентябрь 2007 г.). «Проблема дня рождения». Значимость . 4 (3). Королевское статистическое общество: 124–127. doi : 10.1111/j.1740-9713.2007.00246.x .
^ Матис, Фрэнк Х. (июнь 1991 г.). «Обобщенная проблема дней рождения». SIAM Review . 33 (2): 265–270. doi :10.1137/1033051. ISSN 0036-1445. JSTOR 2031144. OCLC 37699182.
^ Джим Грей, Кэтрин ван Инген. Эмпирические измерения частоты отказов дисков и частоты ошибок
^ Д. Бринк, (Вероятно) точное решение проблемы дней рождения, Ramanujan Journal, 2012, [1].
^ Бринк 2012, Теорема 2
^ ab Brink 2012, Теорема 3
^ ab Brink 2012, Таблица 3, Гипотеза 1
^ "Минимальное количество людей, дающее 50% вероятность иметь по крайней мере n совпадающих дней рождения в течение одного года". Онлайновая энциклопедия целочисленных последовательностей . OEIS . Получено 17 февраля 2020 г.
^ Suzuki, K.; Tonien, D.; et al. (2006). «Парадокс дня рождения для множественных столкновений». В Rhee MS, Lee B. (ред.). Lecture Notes in Computer Science, т. 4296. Berlin: Springer. doi :10.1007/11927587_5. Информационная безопасность и криптология – ICISC 2006.
^ ZE Schnabel (1938) Оценка общей популяции рыб в озере , American Mathematical Monthly 45 , 348–352.
^ MC Wendl (2003) Вероятность столкновения между наборами случайных величин , Statistics and Probability Letters 64 (3), 249–254.
^ ab M. Abramson и WOJ Moser (1970) Еще больше сюрпризов ко дню рождения , American Mathematical Monthly 77 , 856–858
^ Might, Matt. "Коллизии хэш-коллизий с парадоксом дней рождения". Блог Мэтта Might . Получено 17 июля 2015 г.
^ Кнут, Д. Э. (1973). Искусство программирования . Том 3, Сортировка и поиск. Reading, Массачусетс: Addison-Wesley. ISBN 978-0-201-03803-3.
^ Flajolet, P.; Grabner, PJ; Kirschenhofer, P.; Prodinger, H. (1995). «О Q-функции Рамануджана». Журнал вычислительной и прикладной математики . 58 : 103–116. doi : 10.1016/0377-0427(93)E0258-N .
^ Кормен и др. Введение в алгоритмы .
^ Флетчер, Джеймс (16 июня 2014 г.). «Парадокс дня рождения на чемпионате мира». bbc.com . BBC . Получено 27 августа 2015 г. .
^ Ворачек, М.; Тран, США; Форман, АК (2008). «Проблемы с днем рождения и партнером по рождению: заблуждения относительно вероятности среди студентов-психологов, посетителей и персонала казино». Perceptual and Motor Skills . 106 (1): 91–103. doi :10.2466/pms.106.1.91-103. PMID 18459359. S2CID 22046399.
^ Borgs, C.; Chayes, J.; Pittel, B. (2001). «Фазовый переход и конечномерное масштабирование в задаче целочисленного разбиения». Случайные структуры и алгоритмы . 19 (3–4): 247–288. doi :10.1002/rsa.10004. S2CID 6819493.

Библиография

Абрамсон, М.; Мозер, У.О.Дж. (1970). «Больше сюрпризов на день рождения». American Mathematical Monthly . 77 (8): 856–858. doi :10.2307/2317022. JSTOR 2317022.
Блум, Д. (1973). «Проблема дня рождения». American Mathematical Monthly . 80 (10): 1141–1142. doi :10.2307/2318556. JSTOR 2318556.
Кемени, Джон Г.; Снелл, Дж. Лори; Томпсон, Джеральд (1957). Введение в конечную математику (первое издание).
МакКинни, Э. Х. (1966). «Обобщенная задача о днях рождения». American Mathematical Monthly . 73 (5): 385–387. doi :10.2307/2315408. JSTOR 2315408.
Мостеллер, Ф. (1962). «Понимание проблемы дня рождения». Учитель математики . 55 (5): 322–325. doi :10.5951/MT.55.5.0322. JSTOR 27956609.Перепечатано в Mosteller, Frederick (2006). "Understanding the Birthday Problem". Избранные статьи Frederick Mosteller . Springer Series in Statistics. стр. 349–353. doi :10.1007/978-0-387-44956-2_21. ISBN 978-0-387-20271-6.
Шнепс, Лейла ; Колмез, Корали (2013). «Математическая ошибка номер 5. Дело Дианы Сильвестр: анализ методом холодного удара». Математика на суде. Как числа используются и злоупотребляют в зале суда . Базовые книги. ISBN 978-0-465-03292-1.
Sy M. Blinder (2013). Руководство по основам математики: обзор для студентов физики, химии и инженерии. Elsevier. стр. 5–6. ISBN 978-0-12-407163-6.

Внешние ссылки

Парадокс дней рождения, объясняющий дни рождения в високосные годы
Вайсштейн, Эрик В. «Проблема дня рождения». Математический мир .
Юмористическая статья, объясняющая парадокс
SOCR EduMaterials деятельность день рождения эксперимент
Понимание проблемы дня рождения (лучшее объяснение)
Евродни рождения 2012. Задача о днях рождения. Практический футбольный пример парадокса дней рождения.
Грайм, Джеймс. "23: Birthday Probability". Numberphile . Брэди Харан . Архивировано из оригинала 2017-02-25 . Получено 2013-04-02 .
Вычисление вероятностей задачи о днях рождения в WolframAlpha

Проблема с днем ​​рождения