n-вектор

Представление n -вектора ( также называемое геодезической нормалью или вектором нормали эллипсоида ) представляет собой трехпараметрическое невырожденное представление, хорошо подходящее для замены геодезических координат ( широты и долготы ) для представления горизонтального положения в математических вычислениях и компьютерных алгоритмах.

Геометрически n- вектор для заданного положения на эллипсоиде является направленным наружу единичным вектором , который является нормальным в этом положении к эллипсоиду. Для представления горизонтальных положений на Земле эллипсоид является референц-эллипсоидом , а вектор разлагается в геоцентрической системе координат , фиксированной на Земле . Он ведет себя плавно во всех положениях Земли и обладает математическим свойством «один к одному» .

В более общем смысле, эта концепция может быть применена к представлению позиций на границе строго выпуклого ограниченного подмножества k -мерного евклидова пространства , при условии, что эта граница является дифференцируемым многообразием . В этом общем случае n -вектор состоит из k параметров.

Общие свойства

Нормальный вектор к строго выпуклой поверхности может быть использован для однозначного определения положения поверхности. n -вектор — это направленный наружу нормальный вектор с единичной длиной, используемый в качестве представления положения. ^[1]

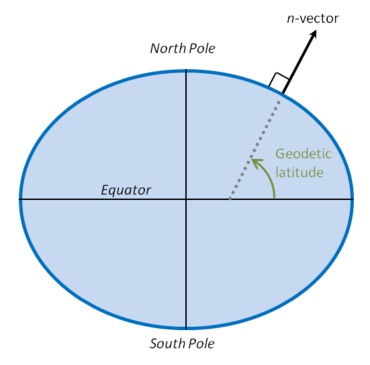
Для большинства приложений поверхность является референц-эллипсоидом Земли, и, таким образом, n -вектор используется для представления горизонтального положения. Следовательно, угол между n -вектором и экваториальной плоскостью соответствует геодезической широте , как показано на рисунке.

Направление n -вектора соответствует геодезической широте.

Положение поверхности имеет две степени свободы , и, таким образом, двух параметров достаточно для представления любого положения на поверхности. На референц-эллипсоиде широта и долгота являются общими параметрами для этой цели, но, как и все двухпараметрические представления , они имеют особенности . Это похоже на ориентацию , которая имеет три степени свободы, но все трехпараметрические представления имеют особенности. ^[2] В обоих случаях особенности избегаются путем добавления дополнительного параметра, т. е. использования n- вектора (три параметра) для представления горизонтального положения и единичного кватерниона (четыре параметра) для представления ориентации .

n- вектор является однозначным представлением, то есть любая позиция поверхности соответствует одному уникальному n -вектору, а любой n -вектор соответствует одной уникальной позиции поверхности.

Поскольку вектор является евклидовым трехмерным , для вычисления положения можно использовать стандартную трехмерную векторную алгебру , что делает n -вектор хорошо подходящим для большинства вычислений горизонтального положения.

Преобразование широты/долготы вн-вектор

На основании определения системы координат ECEF , называемой e , становится ясно, что переход от широты/долготы к n -вектору достигается следующим образом:

${\displaystyle \mathbf {n} ^{e}=\left[{\begin{matrix}\cos(\mathrm {latitude} )\cos(\mathrm {longitude} )\\\cos(\mathrm {latitude} )\sin(\mathrm {longitude} )\\\sin(\mathrm {latitude} )\\\end{matrix}}\right]}$

Верхний индекс e означает, что n -вектор разлагается в системе координат e (т.е. первый компонент является скалярной проекцией n- вектора на ось x системы e , второй - на ось y системы e и т.д.). Обратите внимание, что уравнение является точным как для сферической, так и для эллипсоидальной модели Земли.

Преобразованиен-вектор широты/долготы

Из трех компонентов вектора n , , и , широту можно найти, используя: ${\displaystyle n_{x}^{e}}$ ${\displaystyle n_{y}^{e}}$ ${\displaystyle n_{z}^{e}}$

${\displaystyle \mathrm {latitude} =\arcsin \left(n_{z}^{e}\right)=\arctan \left({\frac {n_{z}^{e}}{\sqrt {{n_{x}^{e}}^{2}+{n_{y}^{e}}^{2}}}}\right)}$

Крайнее правое выражение лучше всего подходит для реализации компьютерной программы. ^[1]

Долгота определяется с помощью:

${\displaystyle \mathrm {longitude} =\arctan \left({\frac {n_{y}^{e}}{n_{x}^{e}}}\right)}$

В этих выражениях следует реализовать вызов atan2 ( y , x ). Сингулярность полюса долготы очевидна, поскольку atan2 (0,0) не определено. Обратите внимание, что уравнения точны как для сферической, так и для эллипсоидальной модели Земли. ${\displaystyle \arctan(y/x)}$

Пример: расстояние по дуге большого круга

Нахождение расстояния по большому кругу между двумя горизонтальными положениями (предполагая, что Земля сферическая) обычно выполняется с помощью широты и долготы. Распространены три различных выражения для этого расстояния; первое основано на arccos , второе основано на arcsin , а последнее основано на arctan . Выражения, которые последовательно усложняются, чтобы избежать числовой нестабильности , нелегко найти, и поскольку они основаны на широте и долготе, сингулярности полюса могут стать проблемой. Они также содержат дельты широты и долготы, которые в целом следует использовать с осторожностью вблизи меридиана ± 180° и полюсов.

Решение той же задачи с использованием n -вектора проще из-за возможности использования векторной алгебры . Выражение arccos получается из скалярного произведения , в то время как величина векторного произведения дает выражение arcsin. Объединение этих двух дает выражение arctan: ^[1]

${\displaystyle {\begin{aligned}&\Delta \sigma =\arccos \left(\mathbf {n} _{a}\cdot \mathbf {n} _{b}\right)\\&\Delta \sigma =\arcsin \left(\left|\mathbf {n} _{a}\times \mathbf {n} _{b}\right|\right)\\&\Delta \sigma =\arctan \left({\frac {\left|\mathbf {n} _{a}\times \mathbf {n} _{b}\right|}{\mathbf {n} _{a}\cdot \mathbf {n} _{b}}}\right)\\\end{aligned}}}$

где и являются n -векторами, представляющими два положения a и b . является угловой разностью, и, таким образом, расстояние по большому кругу достигается путем умножения на радиус Земли. Это выражение также работает на полюсах и на меридиане ±180°. ${\displaystyle \mathbf {n} _{a}}$ ${\displaystyle \mathbf {n} _{b}}$ ${\displaystyle \Delta \sigma }$

Существует несколько других примеров, когда использование векторной алгебры упрощает стандартные проблемы. ^[1] Для общего сравнения различных представлений см. страницу представлений горизонтального положения .

Смотрите также

• Пути земного сечения
• Горизонтальное представление положения
• Широта
• Долгота
• Универсальная поперечная система координат Меркатора
• Кватернион

Ссылки

1. Гейд, Кеннет (2010). "Несингулярное представление горизонтальной позиции" (PDF) . Журнал навигации . 63 (3). Cambridge University Press: 395–417. Bibcode :2010JNav...63..395G. doi :10.1017/S0373463309990415.
2. Штюелпнагель, Джон (1964). «О параметризации трехмерной группы вращения». Обзор SIAM . 6 (4). Общество промышленной и прикладной математики: 422–430. Bibcode : 1964SIAMR...6..422S. doi : 10.1137/1006093. JSTOR  2027966.

Внешние ссылки

• Решение 10 задач с помощью n-вектора