Карандаш (геометрия)

Семейство геометрических объектов с общим свойством

Несколько линий карандашом через А

В геометрии карандаш — это семейство геометрических объектов с общим свойством, например, множество прямых , проходящих через заданную точку на плоскости , или множество окружностей , проходящих через две заданные точки на плоскости.

Хотя определение карандаша довольно расплывчато, общей характеристикой является то, что карандаш полностью определяется любыми двумя своими членами. Аналогично, набор геометрических объектов, которые определяются любыми тремя своими членами, называется пучком . [ ^1] Таким образом, набор всех линий, проходящих через точку в трехмерном пространстве, является пучком линий, любые две из которых определяют пучок линий. Чтобы подчеркнуть двумерную природу такого карандаша, его иногда называют плоским карандашом . ^[2]

Любой геометрический объект может быть использован в карандаше. Наиболее распространенными являются линии, плоскости, окружности, конические сечения, сферы и общие кривые. Могут быть использованы даже точки. Пучок точек — это множество всех точек на данной прямой. ^[1] Более распространенный термин для этого множества — диапазон точек.

Карандаш линий

В плоскости пусть и будут двумя различными пересекающимися прямыми. Для конкретности предположим, что имеет уравнение, и имеет уравнение . Тогда ${\displaystyle \ell }$ ${\displaystyle \ell '}$ ${\displaystyle \ell }$ ${\displaystyle aX+bY+c=0}$ ${\displaystyle \ell '}$ ${\displaystyle a'X+b'Y+c'=0}$

${\displaystyle \lambda \ell +\mu \ell '=0}$,

представляет, для подходящих скаляров и , любую линию, проходящую через пересечение и . Этот набор линий, проходящих через общую точку, называется пучком линий . ^[3] Общая точка пучка линий называется вершиной пучка. ${\displaystyle \lambda }$ ${\displaystyle \mu }$ ${\displaystyle \ell =0}$ ${\displaystyle \ell '=0}$

В аффинной плоскости с рефлексивным вариантом параллельности набор параллельных прямых образует класс эквивалентности, называемый пучком параллельных прямых . ^[4] Эта терминология согласуется с приведенным выше определением, поскольку в уникальном проективном расширении аффинной плоскости до проективной плоскости к каждой прямой в пучке параллельных прямых добавляется одна точка ( точка на бесконечности ), тем самым делая его пучком в указанном выше смысле в проективной плоскости.

Карандаш из плоскостей

Четыре плоскости из осевого пучка на P1 P2

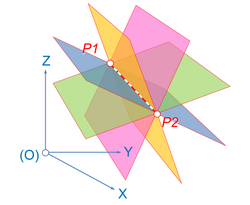
Пучок плоскостей — это множество плоскостей, проходящих через заданную прямую линию в трехмерном пространстве, называемую осью карандаша. Карандаш иногда называют аксиальным карандашом ^[5] или веером плоскостей или пучком плоскостей ^[6] . Например, меридианы земного шара определяются пучком плоскостей на оси вращения Земли.

Две пересекающиеся плоскости пересекаются в одной линии в трехмерном пространстве и, таким образом, определяют ось, а следовательно, и все плоскости в пучке.

Четырехмерное пространство кватернионов можно рассматривать как осевой пучок комплексных плоскостей, все из которых разделяют одну и ту же действительную прямую. Фактически, кватернионы содержат сферу мнимых единиц , т. е . . А пара антиподальных точек на этой сфере вместе с действительной осью порождают комплексную плоскость. Объединение всех этих комплексных плоскостей составляет 4-алгебру кватернионов. ${\displaystyle \mathbb {H} =\{a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} |a,b,c,d\in \mathbb {R} \}}$ ${\displaystyle \{b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} |(b,c,d)\in S^{2}\}}$

Карандаш из кругов

Аполлоновы окружности , два ортогональных пучка окружностей

Любые две окружности на плоскости имеют общую радикальную ось , которая является линией, состоящей из всех точек, которые имеют одинаковую мощность по отношению к двум окружностям. Пучок окружностей (или коаксиальная система ) является множеством всех окружностей на плоскости с одной и той же радикальной осью. ^[7] Чтобы быть инклюзивными, говорят, что концентрические окружности имеют линию на бесконечности в качестве радикальной оси.

Существует пять типов пучков окружностей, ^[8] два семейства аполлоновых окружностей на иллюстрации выше представляют два из них. Каждый тип определяется двумя окружностями, называемыми образующими пучка. При алгебраическом описании возможно, что уравнения могут допускать мнимые решения. Типы следующие:

• Эллиптический пучок (красное семейство окружностей на рисунке) определяется двумя образующими, которые проходят друг через друга ровно в двух точках. Каждая окружность эллиптического пучка проходит через те же две точки. Эллиптический пучок не включает в себя никаких воображаемых окружностей.
• Гиперболический пучок (синее семейство окружностей на рисунке) определяется двумя образующими, которые не пересекаются друг с другом ни в одной точке. Он включает в себя действительные окружности, мнимые окружности и две вырожденные точечные окружности, называемые точками Понселе пучка. Каждая точка на плоскости принадлежит ровно одной окружности пучка.
• Параболический пучок (как предельный случай) определяется, когда две образующие окружности касаются друг друга в одной точке. Он состоит из семейства действительных окружностей, все из которых касаются друг друга в одной общей точке. Вырожденная окружность с радиусом ноль в этой точке также принадлежит пучку.
• Семейство концентрических окружностей с общим центром (можно считать частным случаем гиперболического пучка, где другая точка является точкой в ​​бесконечности).
• Семейство прямых линий, проходящих через общую точку; их следует интерпретировать как окружности, которые все проходят через точку в бесконечности (можно считать частным случаем эллиптического пучка). ^{[9] [10]}

Характеристики

Окружность, ортогональная двум фиксированным окружностям, ортогональна любой окружности в пучке, который они определяют. ^[11]

Окружности, ортогональные двум фиксированным окружностям, образуют пучок окружностей. ^[11]

Две окружности определяют два пучка, единственный пучок, который их содержит, и пучок окружностей, ортогональных им. Радикальная ось одного пучка состоит из центров окружностей другого пучка. Если один пучок эллиптического типа, другой — гиперболического типа и наоборот. ^[11]

Радикальная ось любого пучка окружностей, интерпретируемая как окружность бесконечного радиуса, принадлежит пучку. Любые три окружности принадлежат общему пучку, если все три пары имеют одну и ту же радикальную ось и их центры коллинеарны .

Проективное пространство окружностей

Между окружностями на плоскости и точками в трехмерном проективном пространстве существует естественное соответствие (см. ниже); прямой в этом пространстве соответствует одномерное непрерывное семейство окружностей, следовательно, пучок точек в этом пространстве является пучком окружностей на плоскости.

В частности, уравнение окружности радиуса с центром в точке , ${\displaystyle r}$ ${\displaystyle (p,q)}$

${\displaystyle (x-p)^{2}+(y-q)^{2}=r^{2},}$

можно переписать как

${\displaystyle \alpha (x^{2}+y^{2})-2\beta x-2\gamma y+\delta =0,}$

где . В этой форме умножение четверки на скаляр производит другую четверку, которая представляет ту же окружность; таким образом, эти четверки можно считать однородными координатами для пространства окружностей. ^[12] Прямые линии также могут быть представлены уравнением этого типа, в котором и следует рассматривать как вырожденную форму окружности. Когда , мы можем решить для , и ; последняя формула может дать (в этом случае окружность вырождается в точку) или равную мнимому числу (в этом случае говорят, что четверка представляет воображаемую окружность ). ${\displaystyle \alpha =1,\beta =p,\gamma =q,\delta =p^{2}+q^{2}-r^{2}}$ ${\displaystyle (\alpha ,\beta ,\gamma ,\delta )}$ ${\displaystyle \alpha =0}$ ${\displaystyle \alpha \neq 0}$ ${\displaystyle p=\beta /\alpha ,q=\gamma /\alpha }$ ${\displaystyle r={\sqrt {p^{2}+q^{2}-r^{2}}}}$ ${\displaystyle r=0}$ ${\displaystyle r}$ ${\displaystyle (\alpha ,\beta ,\gamma ,\delta )}$

Множество аффинных комбинаций двух окружностей , то есть множество окружностей, представленных четверкой ${\displaystyle (\alpha _{1},\beta _{1},\gamma _{1},\delta _{1})}$ ${\displaystyle (\alpha _{2},\beta _{2},\gamma _{2},\delta _{2})}$

${\displaystyle z(\alpha _{1},\beta _{1},\gamma _{1},\delta _{1})+(1-z)(\alpha _{2},\beta _{2},\gamma _{2},\delta _{2})}$

для некоторого значения параметра образует пучок, причем две окружности являются образующими пучка. ${\displaystyle z}$

Кардиоида как огибающая пучка окружностей

кардиоида как огибающая пучка кругов

Другой тип пучка окружностей может быть получен следующим образом. Рассмотрим заданную окружность (называемую образующей окружностью ) и выделенную точку P на образующей окружности. Множество всех окружностей, которые проходят через P и имеют свои центры на образующей окружности, образуют пучок окружностей. Огибающая этого пучка является кардиоидой .

Карандаш из сфер

Сфера однозначно определяется четырьмя точками, которые не лежат в одной плоскости . В более общем смысле сфера однозначно определяется четырьмя условиями, такими как прохождение через точку, касание плоскости и т. д. ^[13] Это свойство аналогично свойству, согласно которому три неколлинеарные точки определяют единственную окружность на плоскости.

Следовательно, сфера однозначно определяется (то есть проходит через) окружностью и точкой, не лежащей в плоскости этой окружности.

Рассматривая общие решения уравнений двух сфер , можно увидеть, что две сферы пересекаются по окружности, а плоскость, содержащая эту окружность, называется радикальной плоскостью пересекающихся сфер. ^[14] Хотя радикальная плоскость является действительной плоскостью, окружность может быть мнимой (сферы не имеют общей действительной точки) или состоять из одной точки (сферы касаются в этой точке). ^[15]

Если и являются уравнениями двух различных сфер, то ${\displaystyle f(x,y,z)=0}$ ${\displaystyle g(x,y,z)=0}$

${\displaystyle \lambda f(x,y,z)+\mu g(x,y,z)=0}$

также является уравнением сферы для произвольных значений параметров и . Множество всех сфер, удовлетворяющих этому уравнению, называется пучком сфер, определяемым исходными двумя сферами. В этом определении сфера может быть плоскостью (бесконечный радиус, центр на бесконечности), и если обе исходные сферы являются плоскостями, то все сферы пучка являются плоскостями, в противном случае в пучке есть только одна плоскость (радикальная плоскость). ^[16] ${\displaystyle \lambda }$ ${\displaystyle \mu }$

Если пучок сфер не состоит из одних плоскостей, то существует три типа пучков: ^[15]

• Если сферы пересекаются по действительной окружности C , то пучок состоит из всех сфер, содержащих C , включая радикальную плоскость. Центры всех обычных сфер в пучке лежат на прямой, проходящей через центр C и перпендикулярной радикальной плоскости.
• Если сферы пересекаются по воображаемой окружности, то все сферы пучка также проходят через эту воображаемую окружность, но как обычные сферы они не пересекаются (не имеют общих действительных точек). Линия центров перпендикулярна радикальной плоскости, которая является действительной плоскостью в пучке, содержащем воображаемую окружность.
• Если сферы пересекаются в точке A , то все сферы в пучке касаются в точке A , а радикальная плоскость является общей касательной плоскостью всех этих сфер. Линия центров перпендикулярна радикальной плоскости в точке A.

Все касательные линии из фиксированной точки радикальной плоскости к сферам пучка имеют одинаковую длину. ^[15]

Радикальная плоскость — это геометрическое место центров всех сфер, ортогональных всем сферам пучка. Более того, сфера, ортогональная любым двум сферам пучка сфер, ортогональна всем им, и ее центр лежит в радикальной плоскости пучка. ^[15]

Карандаш из коник

(Невырожденная) коника полностью определяется пятью точками в общем положении (никаких трех коллинеарных) на плоскости, а система коник, проходящих через фиксированный набор из четырех точек (снова на плоскости и никаких трех коллинеарных), называется пучком коник . ^[17] Четыре общие точки называются базовыми точками пучка. Через любую точку, отличную от базовой точки, проходит одна коника пучка. Это понятие обобщает пучок окружностей.

В проективной плоскости, определенной над алгебраически замкнутым полем, любые две коники встречаются в четырех точках (с учетом кратности) и, таким образом, определяют пучок коник на основе этих четырех точек. Более того, четыре базовые точки определяют три пары прямых ( вырожденные коники через базовые точки, каждая прямая пары содержит ровно две базовые точки), и, таким образом, каждый пучок коник будет содержать не более трех вырожденных коник. ^[18]

Пучок коник можно представить алгебраически следующим образом. Пусть и — две различные коники в проективной плоскости, определенные над алгебраически замкнутым полем . Для каждой пары элементов , оба не равных нулю, выражение: ${\displaystyle C_{1}}$ ${\displaystyle C_{2}}$ ${\displaystyle K}$ ${\displaystyle (\lambda ,\mu )}$ ${\displaystyle K}$

$${\displaystyle \lambda C_{1}+\mu C_{2}}$$

представляет собой конику в пучке, определяемом и . Это символическое представление можно сделать конкретным с небольшим злоупотреблением обозначениями (используя те же обозначения для обозначения объекта, а также уравнения, определяющего объект.) Думая о , скажем, как о тернарной квадратичной форме , тогда есть уравнение "коники ". Другая конкретная реализация была бы получена, если бы думали о как о симметричной матрице 3×3 , которая ее представляет. Если и имеют такие конкретные реализации, то каждый член вышеуказанного пучка будет также. Поскольку настройка использует однородные координаты в проективной плоскости, два конкретных представления (либо уравнения, либо матрицы) дают одну и ту же конику, если они отличаются на ненулевую мультипликативную константу. ${\displaystyle C_{1}}$ ${\displaystyle C_{2}}$ ${\displaystyle C_{1}}$ ${\displaystyle C_{1}=0}$ ${\displaystyle C_{1}}$ ${\displaystyle C_{1}}$ ${\displaystyle C_{1}}$ ${\displaystyle C_{2}}$

Карандаш плоских кривых

В более общем смысле, пучок — это частный случай линейной системы делителей , в которой пространство параметров — проективная прямая . Типичные пучки кривых в проективной плоскости , например, записываются как

${\displaystyle \lambda C+\mu C'=0\,}$

где , — плоские кривые. ${\displaystyle C=0}$ ${\displaystyle C'=0}$

История

Дезаргу приписывают изобретение термина «карандаш линий» ( ordonnance de lignes ). ^[19]

Один из первых авторов современной проективной геометрии Дж. Б. Холстед ввел термины копунктный и плоский карандаш для определения угла : «Прямые с одним и тем же пересечением являются копунктными». Также «Совокупность всех компланарных, копунктных прямых называется плоским карандашом » и «Часть плоского карандаша, ограниченная двумя прямыми в качестве сторон , называется углом ». ^[20]

Смотрите также

• Регулировка пучка
• Карандаш Лефшеца
• Матричный карандаш
• Карандашный луч
• Фибрация
• Локус

Примечания

1. Young 1971, стр. 40
2. Холстед 1906, стр. 9
3. Педоу 1988, стр. 106
4. Артин 1957, стр. 53
5. Холстед 1906, стр. 9
6. Вудс 1961, стр. 12
7. Джонсон 2007, стр. 34
8. Некоторые авторы объединяют типы и сокращают список до трех. Schwerdtfeger (1979, стр. 8–10)
9. Джонсон 2007, стр. 36
10. Швердтфегер 1979, стр. 8–10.
11. Джонсон 2007, стр. 37
12. Пфайфер и Ван Хук 1993.
13. Альберт 2016, стр. 55.
14. Альберт 2016, стр. 57.
15. Вудс 1961, стр. 267.
16. Вудс 1961, стр. 266
17. Фолкнер 1952, стр. 64.
18. Сэмюэл 1988, стр. 50.
19. Самые ранние известные случаи использования некоторых слов из области математики , получено 14 июля 2020 г.
20. Холстед 1906, стр. 9

Ссылки

• Альберт, Авраам Адриан (2016) [1949], Solid Analytic Geometry , Dover, ISBN 978-0-486-81026-3
• Артин, Э. (1957), Геометрическая алгебра , Interscience Publishers
• Фолкнер, TE (1952), Проективная геометрия (2-е изд.), Эдинбург: Oliver and Boyd, ISBN 9780486154893
• Холстед, Джордж Брюс (1906), Синтетическая проективная геометрия, New York Wiley
• Джонсон, Роджер А. (2007) [1929], Advanced Euclidean Geometry , Дувр, ISBN 978-0-486-46237-0
• Педоу, Дэн (1988) [1970], Геометрия / Комплексный курс , Довер, ISBN 0-486-65812-0
• Пфайфер, Ричард Э.; Ван Хук, Кэтлин (1993), «Окружности, векторы и линейная алгебра», Mathematics Magazine , 66 (2): 75–86, doi :10.2307/2691113, JSTOR  2691113
• Сэмюэл, Пьер (1988), Проективная геометрия , Тексты для бакалавров по математике (Лекции по математике), Нью-Йорк: Springer-Verlag, ISBN 0-387-96752-4
• Швердтфегер, Ганс (1979) [1962], Геометрия комплексных чисел: геометрия окружности, преобразование Мёбиуса, неевклидова геометрия , Довер, стр. 8–10.
• Янг, Джон Уэсли (1971) [1930], Проективная геометрия , Монография Каруса № 4, Математическая ассоциация Америки
• Вудс, Фредерик С. (1961) [1922], Высшая геометрия / Введение в передовые методы аналитической геометрии , Довер

Внешние ссылки

• Вайсштейн, Эрик В. , «Карандаш», MathWorld