Моделирование поверхностей свободной формы — это метод проектирования поверхностей свободной формы с помощью систем CAD или CAID .
Технология охватывает две основные области: либо создание эстетических поверхностей ( поверхностей класса А ), которые также выполняют функцию, например, кузовов автомобилей и внешних форм потребительских товаров, либо технических поверхностей для таких компонентов, как лопатки газовых турбин и другие компоненты гидродинамической техники.
Пакеты программного обеспечения САПР используют два основных метода для создания поверхностей. Первый начинается с построения кривых ( сплайнов ), из которых затем вытягивается (сечение вдоль направляющей) или разбивается на сетку (лофтируется) 3D-поверхность.

Второй метод — прямое создание поверхности с помощью манипуляции полюсами/контрольными точками поверхности.

Из этих изначально созданных поверхностей строятся другие поверхности с использованием либо производных методов, таких как смещение или угловое расширение поверхностей, либо посредством соединения и смешивания между группами поверхностей.

Свободная поверхность или свободная поверхность используется в САПР и других программах компьютерной графики для описания поверхности трехмерного геометрического элемента. Свободные поверхности не имеют жестких радиальных размеров, в отличие от обычных поверхностей, таких как плоскости , цилиндры и конические поверхности. Они используются для описания таких форм, как лопатки турбин , кузова автомобилей и корпуса лодок . Первоначально разработанная для автомобильной и аэрокосмической промышленности, свободная поверхность в настоящее время широко используется во всех дисциплинах инженерного проектирования от потребительских товаров до судов. Большинство систем сегодня используют математику неравномерных рациональных B-сплайнов (NURBS) [1] для описания форм поверхности; однако существуют и другие методы, такие как поверхности Гордона или поверхности Кунса .
Формы поверхностей свободной формы (и кривых) не хранятся и не определяются в программном обеспечении САПР в терминах полиномиальных уравнений , а их полюсами, степенью и числом участков (сегментов со сплайновыми кривыми). Степень поверхности определяет ее математические свойства и может рассматриваться как представление формы полиномом с переменными в степени значения степени. Например, поверхность со степенью 1 будет плоской поверхностью поперечного сечения . Поверхность со степенью 2 будет изогнута в одном направлении, в то время как поверхность со степенью 3 может (но не обязательно) один раз измениться с вогнутой на выпуклую кривизну. Некоторые системы САПР используют термин порядок вместо степени . Порядок полинома на единицу больше степени и дает число коэффициентов , а не наибольший показатель степени .

Полюса (иногда называемые контрольными точками ) поверхности определяют ее форму. Естественные края поверхности определяются положениями первого и последнего полюсов. (Обратите внимание, что поверхность может иметь обрезанные границы.) Промежуточные полюса действуют как магниты, притягивающие поверхность в своем направлении. Однако поверхность не проходит через эти точки. Второй и третий полюса, а также определяющие форму, соответственно определяют начальный и касательный углы и кривизну . В одной поверхности патча ( поверхности Безье ) имеется на один полюс больше, чем значений степени поверхности. Поверхностные патчи можно объединить в одну поверхность NURBS; в этих точках находятся линии узлов. Количество узлов будет определять влияние полюсов с каждой стороны и плавность перехода. Гладкость между патчами, известная как непрерывность , часто упоминается в терминах значения C :
Еще два важных аспекта — параметры U и V. Это значения на поверхности в диапазоне от 0 до 1, используемые в математическом определении поверхности и для определения путей на поверхности: например, обрезанный граничный край. Обратите внимание, что они не пропорционально распределены вдоль поверхности. Кривая постоянного U или постоянного V известна как изопериметрическая кривая, или линия U (V). В системах САПР поверхности часто отображаются с их полюсами постоянного U или постоянного V, соединенными вместе линиями; они известны как управляющие полигоны .
При определении формы важным фактором является непрерывность поверхностей — насколько плавно они соединяются друг с другом.
Одним из примеров того, где эффективен эффект поверхности, являются автомобильные кузовные панели. Простого смешивания двух изогнутых участков панели с разными радиусами кривизны вместе, сохранения тангенциальной непрерывности (то есть, чтобы смешанная поверхность не меняла направление внезапно, а плавно) будет недостаточно. Им необходимо иметь непрерывную скорость изменения кривизны между двумя секциями, иначе их отражения будут казаться несвязанными.
Непрерывность определяется с помощью терминов:
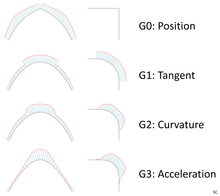
Для достижения высокого качества поверхности NURBS или Безье обычно используются степени 5 и выше.