stringtranslate.com

Двойниковое образование кристаллов

Кварц – Японский близнец
Схема сдвойникованных кристаллов альбита . На более совершенной спайности, параллельной базисной плоскости (P), находится система тонких штрихов, параллельных второй спайности (M).

Двойникование кристаллов происходит, когда два или более соседних кристалла одного и того же минерала ориентированы так, что они разделяют некоторые из общих точек кристаллической решетки симметричным образом. Результатом является срастание двух отдельных кристаллов, которые тесно связаны друг с другом. Поверхность, вдоль которой точки решетки являются общими в двойниковых кристаллах, называется поверхностью состава или плоскостью двойникования.

Кристаллографы классифицируют двойниковые кристаллы по ряду законов двойникования, которые специфичны для кристаллической структуры. Тип двойникования может быть диагностическим инструментом при идентификации минералов. Существует три основных типа двойникования. Первый — это двойникование роста, которое может происходить как в очень больших, так и в очень маленьких частицах. Второй — двойникование трансформации, при котором происходит изменение кристаллической структуры. Третий — двойникование деформации, при котором двойникование развивается в кристалле в ответ на сдвиговое напряжение и является важным механизмом для постоянных изменений формы кристалла.

Определение

Двойная решетка (2D). Длинная горизонтальная красная линия — это композиционная плоскость, где соединяются два кристаллических сегмента. Верхняя кристаллическая решетка — это отражение нижней кристаллической решетки. Красные точки — это общие точки кристаллической решетки.

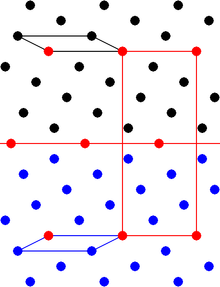
Двойникование — это форма симметричного срастания двух или более соседних кристаллов одного и того же минерала. Оно отличается от обычного случайного срастания минеральных зерен в месторождении минералов, поскольку относительная ориентация двух кристаллических сегментов показывает фиксированную связь, которая характерна для структуры минерала. Связь определяется операцией симметрии, называемой операцией двойникования . [1] [2]

Операция близнеца не является одной из обычных операций симметрии недвойниковой кристаллической структуры. Например, операция близнеца может быть отражением через плоскость, которая не является плоскостью симметрии монокристалла. [1] [2]

На микроскопическом уровне граница двойников характеризуется набором атомных позиций в кристаллической решетке, которые являются общими для двух ориентаций. [1] [2] Эти общие точки решетки придают соединению между сегментами кристалла гораздо большую прочность, чем между случайно ориентированными зернами, так что сдвоенные кристаллы нелегко распадаются. [3]

Параллельный рост описывает форму роста кристаллов, которая создает вид кластера выровненных кристаллов, которые можно ошибочно принять за близнецов. При более внимательном рассмотрении становится ясно, что кластер на самом деле является одним кристаллом. Это не двойникование, поскольку кристаллическая решетка непрерывна по всему кластеру. Параллельный рост, вероятно, происходит, поскольку он снижает энергию системы. [4]

Законы-близнецы

Законы близнецов — это операции симметрии, которые определяют ориентацию между сегментами двойных кристаллов. Они так же характерны для минерала, как и углы его кристаллической грани. Например, кристаллы ставролита показывают двойникование под углами почти точно 90 градусов или 30 градусов. [3] Закон близнецов не является операцией симметрии полного набора базисных точек. [2]

Законы близнецов включают операции отражения, операции вращения и операцию инверсии. Двойникование отражения описывается индексами Миллера плоскости близнеца (т.е. {hkl}), тогда как двойникование вращения описывается направлением оси близнеца (т.е. <hkl>). Двойникование инверсии обычно эквивалентно симметрии отражения или вращения. [1]

Законы вращательного двойникования почти всегда являются 2-кратными вращениями, хотя возможна любая другая разрешенная симметрия вращения (3-кратная, 4-кратная, 5-кратная или 6-кратная). Ось двойникования будет перпендикулярна плоскости решетки. [5] Закон вращательного двойникования может иметь ту же ось, что и вращательная симметрия отдельного кристалла, если закон двойникования является 2-кратным вращением, а операция симметрии является 3-кратным вращением. Это случай двойникования закона шпинели на <111>: структура шпинели имеет 3-кратную вращательную симметрию на <111>, и шпинель обычно двойникуется 2-кратным вращением на <111>. [1]

Граница между сегментами кристалла называется поверхностью состава или, если она плоская, плоскостью состава . Плоскость состава часто, хотя и не всегда, параллельна плоскости закона близнецов закона отражения. Если это так, то плоскость близнецов всегда параллельна возможной грани кристалла. [2]

Общие законы близнецов

Контактное двойникование по шпинельному закону. Слева показан один кристалл с плоскостью состава красным цветом. Справа кристалл фактически был разрезан на плоскости состава, а передняя половина повернута на 180° для получения контактного двойника. Это создает реентеранты вверху, внизу слева и внизу справа от плоскости состава. [3]

В изометрической системе наиболее распространенными типами двойников являются закон шпинели (плоскость двойника, параллельная октаэдру ) <111>, где ось двойника перпендикулярна октаэдрической грани, и железный крест <001>, который представляет собой взаимопроникновение двух пиритоэдров, подтип додекаэдра . [6]

В гексагональной системе кальцит демонстрирует законы контактного двойникования {0001} и {0112}. Кварц демонстрирует бразильский закон {1120} и закон Дофине <0001>, которые являются двойниками проникновения, вызванными трансформацией, и японский закон {1122}, который часто вызывается случайностями во время роста. [6]

В тетрагональной системе циклические контактные двойники являются наиболее часто наблюдаемым типом двойников, например, в рутиловом диоксиде титана и касситерите оксиде олова. [6]

В орторомбической системе кристаллы обычно двойникуются на плоскостях, параллельных грани призмы, причем наиболее распространенным является двойник {110}, который дает циклические двойники, такие как в арагоните , хризоберилле и церуссите . [6]

В моноклинной системе двойники чаще всего встречаются на плоскостях {100} и {001} по закону Манебаха {001}, Карлсбадскому закону [001], закону Бавено {021} в ортоклазе и двойникам типа «ласточкин хвост» (закон Манебаха) {001} в гипсе . [6]

В триклинной системе наиболее часто двойниковые кристаллы — это минералы полевого шпата плагиоклаз и микроклин . Эти минералы демонстрируют законы альбита и периклина. [5] [6]

Наиболее распространенные операции близнецов по кристаллической системе приведены ниже. Этот список не является исчерпывающим, особенно для кристаллических систем с самой низкой симметрией, таких как триклинная система. [7] [1] [6]

30° двойник ставролита
90° двойники ставролита
Железный пирит крест-близнец

Типы побратимства

Хризоберилл, демонстрирующий циклическое двойникование

Простые двойниковые кристаллы могут быть контактными двойниками или двойниками проникновения. Контактные двойники встречаются на одной плоскости состава, часто появляясь как зеркальные отражения по всей границе. Плагиоклаз , кварц , гипс и шпинель часто демонстрируют контактное двойникование. [3] Мероэдрическое двойникование происходит, когда решетки контактных двойников накладываются в трех измерениях, например, путем относительного вращения одного двойника относительно другого. [8] Примером является метацейнерит . [9] Контактное двойникование характерно для создания входящих граней, где грани сегментов кристалла встречаются на контактной плоскости под углом более 180°. [3]

Тип близнецовства, предполагающий 180°-ное соотношение, называется гемитропизмом или гемитропией .

В двойниках проникновения отдельные кристаллы имеют вид проходящих друг через друга симметричным образом. [3] Ортоклаз , ставролит , пирит и флюорит часто показывают двойникование проникновения. Поверхность состава в двойниках проникновения обычно нерегулярна и простирается до центра кристалла. [2]

Контактное двойникование может возникнуть как в результате отражения, так и вращения, тогда как проникающее двойникование обычно возникает в результате вращения. [2]

Если несколько двойниковых частей кристалла выровнены по одному и тому же закону двойников, их называют множественными или повторными двойниками . Если эти множественные двойники выровнены параллельно, их называют полисинтетическими двойниками . Когда множественные двойники не параллельны, они называются циклическими двойниками . Альбит , кальцит и пирит часто демонстрируют полисинтетическое двойникование. Близко расположенное полисинтетическое двойникование часто наблюдается в виде полос или тонких параллельных линий на грани кристалла.Циклические двойники образуются в результате многократного двойникования вокруг оси вращения. Этот тип двойникования происходит вокруг трех, четырех, пяти, шести или восьмикратных осей, соответствующие модели называются threelings, fourlings, fivelings , sixlings и eightlings. Sixlings обычны для арагонита. [10] [11] Рутил , арагонит , церуссит и хризоберилл часто демонстрируют циклическое двойникование, как правило, в радиальном порядке. [3] [2]

При вращательном двойниковании соотношение между осью двойникования и плоскостью двойникования делится на три типа: [12]

  1. параллельное двойникование, когда ось близнеца и композиционная плоскость лежат параллельно друг другу,
  2. нормальное двойникование, когда плоскость двойникования и композиционная плоскость лежат нормально, и
  3. сложное двойникование, сочетание параллельного двойникования и нормального двойникования в одной композиционной плоскости.

Способы формирования

Параллельный рост пироморфита

Существует три способа образования двойниковых кристаллов.

Ростовое двойникование (нанодвойникование)

Пятикратный двойник в золотой наночастице ( микрофотография, полученная с помощью электронного микроскопа ).

В процессе роста могут возникать два типа двойникования: случайное и такое, при котором двойниковая структура имеет более низкую энергию.

При случайном росте двойников атом присоединяется к грани кристалла в неидеальном положении, образуя затравку для роста двойника. Исходный кристалл и его двойник затем растут вместе и очень похожи друг на друга. Это достаточно характерно для некоторых минералов, чтобы предположить, что это термодинамически или кинетически благоприятно в условиях быстрого роста. [3] [1]

От них отличаются близнецы, обнаруженные в наночастицах, таких как на изображении здесь, причем эти пятикратные или декаэдрические наночастицы являются одними из самых распространенных. [14] Эти циклические близнецы возникают, поскольку они имеют более низкую энергию при малых размерах. [15] Для показанного пятикратного случая существует дисклинация вдоль общей оси [16] , которая приводит к дополнительной энергии деформации. [17] Уравновешивая это, происходит снижение поверхностной свободной энергии, в значительной степени из-за большего количества (111) поверхностных граней. [18] В малых наночастицах декаэдрическая и более сложная икосаэдрическая структура (с двадцатью единицами) имеют более низкую энергию, но при более высоких энергиях монокристаллы становятся более низкоэнергетичными. [19] [20] Однако им не нужно превращаться в монокристаллы, и они могут расти очень большими и известны как пятигранники, задокументированные еще в 1831 году Густавом Розе ; [21] Дополнительные рисунки доступны в Атласе кристаллических форм, а также см. статью о пятиугольниках . [22]

Трансформация двойникование

Иллюстрация двойникования в 2-D. Орторомбический кристалл слева трансформируется в моноклинный кристалл справа с двумя параллельными плоскостями двойникования (полисинтетическое двойникование)

Трансформация и отжиговое двойникование происходят, когда охлаждающийся кристалл испытывает сдвиговый полиморфный переход. Например, лейцит имеет изометрическую кристаллическую структуру выше примерно 665 °C (1229 °F), но становится тетрагональным ниже этой температуры. Любая из трех исходных осей кристалла может стать длинной осью, когда происходит этот фазовый переход. Двойникование происходит, когда различные части кристалла нарушают свою изометрическую симметрию вдоль другого выбора оси. Это обычно полисинтетическое двойникование, которое позволяет кристаллу сохранять свою изометрическую форму путем усреднения смещения в каждом направлении. Это дает псевдоморфный кристалл, который, по-видимому, имеет изометрическую симметрию. Калиевый полевой шпат также испытывает полисинтетическое двойникование, поскольку он трансформируется из моноклинной структуры ( ортоклаз ) в триклинную структуру ( микроклин ) при медленном охлаждении. [1]

Деформационное двойникование

Анимация деформационного двойникования кристалла

Двойникование деформации является реакцией на сдвиговое напряжение. Кристаллическая структура смещается вдоль последовательных плоскостей кристалла, этот процесс также называется скольжением . Двойникование всегда является двойникованием отражения, а плоскость скольжения также является плоскостью зеркала. Двойникование деформации можно наблюдать в фрагменте скола кальцита, применяя легкое давление лезвием ножа вблизи края. Это конкретное двойникование скольжения, {102}, встречается почти повсеместно в деформированных пластах горных пород, содержащих кальцит. [1]

Двойникование и скольжение являются конкурирующими механизмами деформации кристаллов. Каждый механизм доминирует в определенных кристаллических системах и при определенных условиях. [23] В металлах с ГЦК-решеткой скольжение почти всегда доминирует, поскольку требуемое напряжение намного меньше напряжения двойникования. [24]

Двойникование может происходить путем кооперативного смещения атомов вдоль грани границы двойника. Это смещение большого количества атомов одновременно требует значительной энергии для выполнения. Поэтому теоретическое напряжение, необходимое для образования двойника, довольно велико. Считается, что двойникование связано с движением дислокаций в скоординированном масштабе, в отличие от скольжения, которое вызывается независимым скольжением в нескольких местах в кристалле .

По сравнению со скольжением, двойникование создает деформационный рисунок, который по своей природе более неоднороден . Эта деформация создает локальный градиент по всему материалу и вблизи пересечений между двойниками и границами зерен. Градиент деформации может привести к разрушению вдоль границ, особенно в ОЦК переходных металлах при низких температурах.

Из трех распространенных кристаллических структур bcc , fcc и hcp , структура hcp наиболее склонна к образованию деформационных двойников при деформации, поскольку они редко имеют достаточное количество систем скольжения для произвольного изменения формы. Высокие скорости деформации, низкая энергия дефекта упаковки и низкие температуры способствуют деформационному двойникованию. [25]

Если металл с гранецентрированной кубической (ГЦК) структурой, такой как Al, Cu, Ag, Au и т. д., подвергается напряжению, он будет испытывать двойникование. Образование и миграция границ двойников частично ответственны за пластичность и ковкость ГЦК металлов. [26]

Двойниковые границы частично ответственны за ударное упрочнение и за многие изменения, которые происходят при холодной обработке металлов с ограниченными системами скольжения или при очень низких температурах. Они также происходят из-за мартенситных превращений : движение двойниковых границ ответственно за псевдоупругое и память формы поведения нитинола , и их присутствие частично ответственно за твердость из-за закалки стали . В некоторых типах высокопрочных сталей очень мелкие деформационные двойники действуют как основные препятствия для движения дислокаций. Эти стали называются сталями «TWIP», где TWIP означает пластичность, вызванную двойникованием . [27]

Кристаллография деформационного двойникования

Деформационное двойникование кристаллографических плоскостей

Двойникование кристаллографически определяется его двойниковой плоскостью 𝑲 𝟏 , зеркальной плоскостью в двойнике и исходном материале, и 𝜼 𝟏, которая является направлением сдвига двойникования. Двойники деформации в Zr обычно имеют линзовидную форму, удлиняясь в направлении 𝜼 𝟏 и утолщаясь вдоль нормали плоскости 𝑲 𝟏 . [28]

Плоскость близнеца, направление сдвига и плоскость сдвига образуют базисные векторы ортогонального набора. Соотношение разориентации оси и угла между родителем и близнецом представляет собой поворот на угол 𝜉 вокруг нормального направления плоскости сдвига 𝑷.

В более общем смысле двойникование можно описать как поворот на 180° вокруг оси (𝑲 𝟏 для близнецов I типа или 𝜼 𝟏 для близнецов II типа в нормальном направлении) или зеркальное отражение в плоскости (𝑲 𝟏 или 𝜼 𝟏 нормальной плоскости). [29]

В дополнение к однородному сдвигу, атомные перетасовки иногда требуются для реформирования правильной кристаллической структуры в двойниковой решетке. Для каждого варианта близнеца возможен обратный близнец с переставленными 𝑲 𝟏 и 𝑲 2 , 𝜼 𝟏 и 𝜼 2 , но один вариант может появляться чаще в реальности из-за сложностей с требуемыми перетасовками. [30]

В сдвиговом действии есть только две кристаллографические плоскости, которые не меняют свою форму и размер в результате сдвига. Первая 𝑲 𝟏 — это плоскость, определяющая верхнюю и нижнюю поверхности сдвинутого объема. Эта плоскость содержит направление сдвига. Другая плоскость, обозначенная C. Направление сдвига показано стрелкой и помечено ее обычным обозначением 𝜼 𝟏 . Из вышесказанного следует, что существует три способа, которыми кристаллическая решетка может быть сдвинута, сохраняя при этом свою кристаллическую структуру и симметрию:

  1. Когда 𝑲 𝟏 — рациональная плоскость, а 𝜼 2 — рациональное направление, близнец первого рода
  2. Когда 𝑲 2 — рациональная плоскость, а 𝜼 𝟏 — рациональное направление, близнец второго рода, редкий
  3. Когда все четыре элемента 𝑲 𝟏 , 𝑲 2 , 𝜼 𝟏 и 𝜼 2 рациональны, то образуется составной близнец

Конфигурация деформационного двойникования

Регулярные плоскости двойникования в кристалле кальцита. Изображение скрещенных николей, увеличение 10× (Поле зрения = 2 мм)

Зародыш двойника деформации образуется в металле BCC путем накопления дефектов упаковки, при этом выбор варианта регулируется локальным напряженным состоянием. [31] [32] [33] Изменение поля напряжений вблизи двойников, выведенное из экспериментальных данных HR- EBSD [34] [35] и данных моделирования конечных элементов кристаллической пластичности (CPFE), показало, что двойники зарождаются на участках с максимальной плотностью энергии деформации и разрешенным напряжением сдвига двойников ; таким образом, уменьшая общую упругую энергию после образования. Эта релаксация зависит от толщины двойника и является решающим фактором в расстоянии между двойниками. [36] Экспериментальный [37] и трехмерный [38] анализ были сосредоточены на (сохраненной) плотности энергии деформации, измеренной вдоль пути. Это высоко локализованное поле напряжений может обеспечить достаточную движущую силу для одновременного зарождения двойников [39] и зарождения межзеренных/внутризеренных трещин .

Рост деформационного двойника можно рассматривать как двухэтапный процесс i) утолщения, опосредованного взаимодействием между остаточными и подвижными парциальными двойниками на когерентном интерфейсе близнец-родитель, [40] и ii) подвижности дислокаций вдоль направления сдвига двойника. [41] Двойник распространяется, когда однородное напряжение сдвига достигает критического значения, и интерфейс близнец-родитель продвигается внутрь родительского зерна [240]. Распространяющийся деформационный двойник создает поле напряжений из-за его ограничения окружающим родительским кристаллом, и деформационные двойники развивают трехмерную сплющенную сфероидальную форму (которая появляется в двумерных сечениях как двояковыпуклая линза ) со смешанным когерентным и некогерентным интерфейсом (рисунок b). [41]

Каннан и др. [42] обнаружили, используя in-situ сверхскоростную оптическую визуализацию, что зарождение двойников в монокристаллическом магнии вызвано напряжением , сопровождающимся мгновенным распространением со скоростью 1 км/с (вначале), которое отдает приоритет объемному боковому утолщению над прямым распространением, после критической ширины, где рост затем становится быстрее вдоль направления сдвига. Барнетт [43] также указал, что рост происходит из-за расширения двойного кончика. Кроме того, упругое моделирование локального поля напряжений , окружающего эллипсоидальный двойной кончик, показывает, что поле можно описать с помощью его угла линзы ( ), и что величина поля напряжений увеличивается с толщиной двойника. [44]

(a) Изображение, полученное с помощью диода форресатных электронов (FSD), для двойников деформации на границе зерен в упрочненном старением феррите при I) рабочем расстоянии 18 мм и II) рабочем расстоянии 38 мм. (b) Схема двояковыпуклого двойника с дислокациями на интерфейсе и (c) Двойниковая полоса. [45]

На практике пластическая аккомодация происходит в исходном кристалле ; таким образом, она также зависит от предела текучести материала, анизотропной упругой жесткости исходной кристаллической решетки и величины сдвига двойникования деформации. [40] Это также может сопровождаться диффузией элементов на большие расстояния и элементной сегрегацией (например, Cr и Co в монокристаллическом суперсплаве на основе Ni MD2), которая происходит на границе двойника, чтобы облегчить рост двойника за счет снижения критической энергии дефекта упаковки. [46] Наблюдалось линейное изменение между толщиной двойника, энергией дефекта упаковки и размером зерна, [47] и, в меньшей степени, напряженным состоянием двойникового зерна ( фактор Шмида ). [48] Толщина двойника насыщалась, как только критическая плотность остаточных дислокаций достигала когерентной границы двойник-исходный кристалл. [33] [49]

Значительное внимание было уделено кристаллографии , [ 50] морфологии [51] и макромеханическим эффектам [52] деформационного двойникования. Хотя критерий роста деформационного двойника не полностью понят, это контролируемое кончиком явление, связанное с взаимодействием между остаточными и подвижными парциальными двойниками на границе раздела двойников; термодинамически это включает упругую энергию напряженной решетки, интерфейс и объемную свободную энергию двойника и рассеянную энергию механизма роста. [53] Чтобы полностью понять взаимодействие между микроструктурой (т. е. размером зерна, текстурой), температурой и скоростью деформации при деформационном двойниковании, крайне важно охарактеризовать (высокое) локальное напряжение и поле деформации, связанные с утолщением и распространением двойников. Это особенно важно для материалов, где разрушение сколом может быть инициировано двойникованием (например, железо-кремний, ферритная фаза упрочненной старением дуплексной нержавеющей стали и монокристаллический магний ) как механизм снятия напряжения.

Ранние исследования деформационных двойников, задержанных в зернах ниобия [54] и железа [55], визуализировали высоколокальную концентрацию деформации на кончике двойника с использованием процедуры травления-ямки. Совсем недавно дифракция обратного рассеяния электронов высокого разрешения (HR- EBSD ) использовалась для исследования «сингулярности» деформации перед кончиком двойника в гексагональном плотноупакованном (HCP) циркониевом сплаве. Деформационный двойник в титане коммерческой чистоты был охарактеризован аналогичным образом, а затем количественно оценен с использованием локального фактора Шмида (LSF) на кончике двойника, [56], как описано в уравнении ниже.

где σ  — тензор напряжений, S i — тензор Шмида, P i — его симметричная часть, d i — направление сдвига, а n i  — нормаль плоскости сдвига для i -й системы скольжения . Авторы пришли к выводу, что условия на вершине двойника контролируют утолщение и распространение способом, аналогичным работе источников дислокаций перед вершиной трещины. [57] В анализе широкая область высокого LSF перед вершиной двойника благоприятствовала распространению, тогда как узкая область высокого LSF способствовала утолщению. С тех пор утверждается [58] , что LSF жестко контролирует выбор варианта двойника, поскольку двойникование имеет сильную полярность.

Новизна LSF — по сравнению с другими критериями для описания условий на двойнике [47] — заключается в объединении геометрического критерия с полем деформации в родительском зерне для получения приблизительного указания на локальный режим двойника (т. е. утолщение или распространение). Однако анализ LSF не использует имеющиеся данные полного поля, полагается на глобальную информацию о приложенном напряжении и не учитывает энергетический баланс, который управляет ростом двойника. Было проведено мало экспериментов in situ для количественной оценки поля деформации перед распространяющимся двойником деформации. [45] [35] Такие наблюдения могут подтвердить геометрические или гибридные критерии, основанные на геометрической энергии [58] для роста. Наномасштабное тестирование (т. е. просвечивающая электронная микроскопия ) может не отражать поведение в объемных образцах из-за недостатка пластичности, т. е. большого отношения площади поверхности к объему, [59], поэтому необходим подходящий метод анализа.

Ллойд [49] описал поле концентрации напряжений перед вершиной двойника, используя двумерную модель на основе дислокации в пределах одного зерна магния . Ван и Ли [60] , которые рассматривали модели микроскопического фазового поля (MPF) трещин, отметили, что поля напряжений были похожи для дислокаций , деформационного двойникования и мартенситных превращений, с различиями только в тяге созданной поверхности, т. е. существует 100% восстановление тяги для дислокаций и поверхность без тяги для трещины. Они подчеркнули, что сингулярность поля напряжений регулирует продвижение вершины трещины и дислокаций . Эту концентрацию напряжений можно охарактеризовать с помощью независимого от пути линейного интеграла , как показано Эшелби для дислокаций, учитывая вклад поверхностного тяги и эллипсоидальных включений , [61] и Райсом [62] для трещин и концентраций напряжений с поверхностями без тяги. Более того, Венейблс [63] отметил, что сплющенная сфероидальная форма двойного кончика является идеальным примером эллипсоидного включения или выемки.

Смотрите также

На Викискладе есть медиафайлы по теме Сдвоенные кристаллы .

Ссылки

  1. ^ abcdefghi Нессе, Уильям Д. (2000). Введение в минералогию . Нью-Йорк: Oxford University Press. С. 87–91. ISBN 9780195106916.
  2. ^ abcdefgh Кляйн, Корнелис; Херлбат, Корнелиус С. младший (1993). Руководство по минералогии : (после Джеймса Д. Даны) (21-е изд.). Нью-Йорк: Wiley. С. 102–106. ISBN 047157452X.
  3. ^ abcdefgh Синканкас, Джон (1964). Минералогия для любителей . Принстон, Нью-Джерси: Van Nostrand. С. 96–105. ISBN 0442276249.
  4. ^ Кляйн и Херлбат 1993, стр. 101.
  5. ^ ab Nelson, Stephen A. (2013). «Побратимство, полиморфизм, политипизм, псевдоморфизм». Университет Тулейна . Получено 19 февраля 2022 г.
  6. ^ abcdefg Кляйн и Херлбат 1993, стр. 104–106.
  7. ^ Нессе 2000, стр. 89, 214–216.
  8. ^ Йетс, Тодд О. (1997). "[22] Обнаружение и преодоление двойникования кристаллов". Макромолекулярная кристаллография, часть A. Методы в энзимологии. Т. 276. С. 344–358. doi :10.1016/S0076-6879(97)76068-3. ISBN 9780121821777. PMID  27799105.
  9. ^ Локок, А. Дж.; Бернс, П. К. (1 апреля 2003 г.). «Кристаллические структуры и синтез медьсодержащих членов групп аутунита и мета-аутунита: торбернит, цейнерит, метаторбернит и метацейнерит». Канадский минералог . 41 (2): 489–502. Bibcode : 2003CaMin..41..489L. doi : 10.2113/gscanmin.41.2.489.
  10. ^ Дьяр и Гюнтер 2008, стр. 41–43.
  11. ^ Честерман и Лоу 2008, стр. 39
  12. ^ Тоби, Александр К. (1961). «Распознавание двойников плагиоклаза в сечениях, нормальных к плоскости состава». American Mineralogist . 46 (11–12): 1470–1488 . Получено 19 февраля 2022 г. .
  13. ^ Кляйн и Херлбат 1993, стр. 167.
  14. ^ Хофмейстер, Х. (1998). <3::aid-crat3>3.0.co;2-3 "Сорок лет изучения пятикратных двойниковых структур в малых частицах и тонких пленках". Crystal Research and Technology . 33 (1): 3–25. Bibcode : 1998CryRT..33....3H. doi : 10.1002/(sici)1521-4079(1998)33:1<3::aid-crat3>3.0.co;2-3. ISSN  0232-1300.
  15. ^ Маркс, Лоуренс. Д. (2023), «Форма, термодинамика и кинетика наночастиц», Энциклопедия наноматериалов , Elsevier, стр. 383–417, doi :10.1016/b978-0-12-822425-0.00082-8, ISBN 978-0-12-822423-6, получено 2023-07-11
  16. ^ Wit, R de (1972). «Частичные дисклинации». Journal of Physics C: Solid State Physics . 5 (5): 529–534. Bibcode : 1972JPhC....5..529D. doi : 10.1088/0022-3719/5/5/004. ISSN  0022-3719.
  17. ^ Howie, A.; Marks, LD (1984). «Упругие деформации и энергетический баланс для многократно двойниковых частиц». Philosophical Magazine A. 49 ( 1): 95–109. Bibcode : 1984PMagA..49...95H. doi : 10.1080/01418618408233432. ISSN  0141-8610.
  18. ^ Marks, LD (1984). «Структура поверхности и энергетика многократно двойниковых частиц». Philosophical Magazine A. 49 ( 1): 81–93. Bibcode : 1984PMagA..49...81M. doi : 10.1080/01418618408233431. ISSN  0141-8610.
  19. ^ Балетто, Франческа; Феррандо, Риккардо (2005). «Структурные свойства нанокластеров: энергетические, термодинамические и кинетические эффекты». Reviews of Modern Physics . 77 (1): 371–423. Bibcode : 2005RvMP...77..371B. doi : 10.1103/RevModPhys.77.371. ISSN  0034-6861.
  20. ^ Роджерс, Блейк; Лер, Александр; Веласкес-Салазар, Х. Хесус; Уэттен, Роберт; Мендоса-Крус, Рубен; Базан-Диас, Лурдес; Бахена-Урибе, Даниэль; Хосе Якаман, Мигель (2023). «Декаэдры и икосаэдры повсюду: аномальная кристаллизация золота и других металлов в наномасштабе». Crystal Research and Technology . 58 (4). Bibcode : 2023CryRT..5800259R. doi : 10.1002/crat.202200259. ISSN  0232-1300.
  21. ^ Роза, Густав (1831). «Ueber die Krystallformen des Goldes und des Silbers». Аннален дер Физик . 99 (10): 196–204. Бибкод : 1831АнП....99..196Р. дои : 10.1002/andp.18310991003. ISSN  0003-3804.
  22. ^ Гольдшмидт, V (1918). Atlas der Kristallformen, V4, Таблички. Университет Карла Винтерса. с. Тафель 48, рис. 21. (Золото). hdl : 2027/nyp.33433084029887.
  23. ^ Махаджан, С.; Уильямс, ДФ (июнь 1973 г.). «Деформационное двойникование в металлах и сплавах». International Metallurgical Reviews . 18 (2): 43–61. doi :10.1179/imtlr.1973.18.2.43.
  24. ^ Бейерлейн, Ирен Дж.; Мара, Натан А.; Бхаттачарья, Дхрити; Александр, Дэвид Дж.; Неккер, Карл Т. (январь 2011 г.). «Эволюция текстуры посредством комбинированного скольжения и деформационного двойникования в катаном эвтектическом нанокомпозите из литого серебра и меди». Международный журнал пластичности . 27 (1): 121–146. doi :10.1016/j.ijplas.2010.05.007.
  25. ^ Кортни, Томас Х. (2000) Механическое поведение материалов , 2-е изд. McGraw Hill. ISBN 1-57766-425-6 
  26. ^ Нурул Акмал Че, Лах; Тригерос, Соня (2019). «Синтез и моделирование механических свойств нанопроволок Ag, Au и Cu». Sci. Technol. Adv. Mater . 20 (1): 225–261. Bibcode : 2019STAdM..20..225L. doi : 10.1080/14686996.2019.1585145. PMC 6442207. PMID  30956731. 
  27. ^ Steinmetz, DR; Jäpel, T.; Wietbrock, B.; Eisenlohr, P.; Gutierrez-Urrutia, I.; Saeed (2013), "Выявление деформационного упрочнения сталей с пластичностью, вызванной двойникованием: теория, моделирование, эксперименты", Acta Materialia , 61 (2): 494, Bibcode : 2013AcMat..61..494S, doi : 10.1016/j.actamat.2012.09.064.
  28. ^ Кристиан, Дж. В.; Махаджан, С. (1995). «Деформационное двойникование». Прогресс в материаловедении . 39 (1–2): 1–157. doi :10.1016/0079-6425(94)00007-7.
  29. ^ Calhoun, CA; Garlea, E.; Sisneros, TA; Agnew, SR (апрель 2018 г.). «In-situ нейтронная дифракционная характеристика температурной зависимости деформации в α-уране». Journal of Nuclear Materials . 502 : 60–67. Bibcode :2018JNuM..502...60C. doi : 10.1016/j.jnucmat.2018.01.036 . OSTI  1478070.
  30. ^ Bilby, BA; Crocker, AG (1965-10-26). «Теория кристаллографии деформационного двойникования». Труды Лондонского королевского общества. Серия A. Математические и физические науки . 288 (1413): 240–255. Bibcode :1965RSPSA.288..240B. doi :10.1098/rspa.1965.0216. ISSN  0080-4630. S2CID  120566509.
  31. ^ Cahn, RW (октябрь 1954). «Двойниковые кристаллы». Advances in Physics . 3 (12): 363–445. Bibcode :1954AdPhy...3..363C. doi :10.1080/00018735400101223. ISSN  0001-8732.
  32. ^ Wang, S.; Schuman, C.; Bao, L.; Lecomte, JS; Zhang, Y.; Raulot, JM; Philippe, MJ; Zhao, X.; Esling, C. (май 2012 г.). «Критерий выбора варианта для двойных вариантов в титановых сплавах, деформированных прокаткой» (PDF) . Acta Materialia . 60 (9): 3912–3919. Bibcode :2012AcMat..60.3912W. doi :10.1016/j.actamat.2012.03.046.
  33. ^ ab Christian, JW (2002). "Деформационное двойникование". Теория превращений в металлах и сплавах . Elsevier. стр. 859–960. doi :10.1016/b978-008044019-4/50025-8. ISBN 978-0-08-044019-4.
  34. ^ Абдолванд, Хамидреза; Седагхат, Омид; Го, Йи (октябрь 2018 г.). «Зарождение и рост { 11 2 2 } двойников в титане: поля упругой энергии и напряжений вблизи двойников». Materialia . 2 : 58–62. doi :10.1016/j.mtla.2018.06.012. S2CID  139852253.
  35. ^ ab Guo, Y.; Schwiedrzik, J.; Michler, J.; Maeder, X. (2016-11-01). «О зарождении и росте двойника {112¯2} в титане коммерческой чистоты: исследование локального поля напряжений и распределения плотности дислокаций in situ». Acta Materialia . 120 : 292–301. doi :10.1016/j.actamat.2016.08.073. ISSN  1359-6454.
  36. ^ Паудель, ЮбРадж; Барретт, Кристофер Д.; Чопп, Марк А.; Инал, Каан; Эль Кадири, Хайтам (июль 2017 г.). «За пределами первоначального зарождения двойников в металлах с ГПУ-структурой: микромеханическая формулировка для определения расстояния между двойниками во время деформации». Acta Materialia . 133 : 134–146. Bibcode :2017AcMat.133..134P. doi : 10.1016/j.actamat.2017.05.013 . ISSN  1359-6454.
  37. ^ Paramatmuni, Chaitanya; Zheng, Zebang; Rainforth, W. Mark; Dunne, Fionn PE (2020-12-01). "Зарождение двойников и выбор варианта в сплавах Mg: комплексное моделирование пластичности кристаллов и экспериментальный подход" (PDF) . International Journal of Plasticity . 135 : 102778. doi :10.1016/j.ijplas.2020.102778. ISSN  0749-6419. S2CID  224887964.
  38. ^ Paramatmuni, Chaitanya; Guo, Yi; Withers, Philip J.; Dunne, Fionn PE (2021-08-01). "Трехмерное механистическое исследование драйверов классического зарождения двойников и выбора вариантов в сплавах Mg: мезомасштабное моделирование и экспериментальное исследование". International Journal of Plasticity . 143 : 103027. doi : 10.1016/j.ijplas.2021.103027. hdl : 10044/1/90290 . ISSN  0749-6419. S2CID  236612852.
  39. ^ Арул Кумар, М.; Байерляйн, Эй-Джей; Томе, Китай (01 сентября 2016 г.). «Влияние локальных полей напряжений на двойниковые характеристики в металлах ГПУ». Акта Материалия . 116 : 143–154. Бибкод : 2016AcMat.116..143A. дои : 10.1016/j.actamat.2016.06.042 . ISSN  1359-6454.
  40. ^ ab Beyerlein, Irene J.; Zhang, Xinghang; Misra, Amit (июль 2014 г.). «Growth Twins and Deformation Twins in Metals». Annual Review of Materials Research . 44 (1): 329–363. Bibcode : 2014AnRMS..44..329B. doi : 10.1146/annurev-matsci-070813-113304 . ISSN  1531-7331.
  41. ^ ab Britton, TB; Dunne, FPE; Wilkinson, AJ (2015-06-08). "О механистической основе деформации на микроуровне в гексагональных плотноупакованных металлах". Труды Королевского общества A: Математические, физические и инженерные науки . 471 (2178): 20140881. Bibcode : 2015RSPSA.47140881B. doi : 10.1098/rspa.2014.0881 . S2CID  138085929.
  42. ^ Лю, Y.; Тан, PZ; Гонг, MY; МакКейб, RJ; Ван, J.; Томе, CN (2019-07-25). "Трехмерный характер деформационного двойника в магнии". Nature Communications . 10 (1): 3308. Bibcode :2019NatCo..10.3308L. doi :10.1038/s41467-019-10573-7. ISSN  2041-1723. PMC 6658514 . PMID  31346160. 
  43. ^ Барнетт, MR (2007-08-25). «Двойникование и пластичность магниевых сплавов: Часть I: «Растягивающиеся» двойники». Материаловедение и машиностроение: A . 464 (1): 1–7. doi :10.1016/j.msea.2006.12.037. ISSN  0921-5093.
  44. ^ Арул Кумар, М.; Канджарла, АК; Низгода, СР; Лебенсон, РА; Томе, Китай (01 февраля 2015 г.). «Численное исследование напряженного состояния двойника деформации в магнии». Акта Материалия . 84 : 349–358. дои : 10.1016/j.actamat.2014.10.048 . ISSN  1359-6454.
  45. ^ ab Koko, Abdalrhaman; Elmukashfi, Elsiddig; Dragnevski, Kalin; Wilkinson, Angus J.; Marrow, Thomas James (2021-10-01). "J-интегральный анализ полей упругой деформации ферритовых деформационных двойников с использованием дифракции обратного рассеяния электронов". Acta Materialia . 218 : 117203. Bibcode : 2021AcMat.21817203K. doi : 10.1016/j.actamat.2021.117203. ISSN  1359-6454.
  46. ^ Barba, D.; Alabort, E.; Pedrazzini, S.; Collins, DM; Wilkinson, AJ; Bagot, PAJ; Moody, MP; Atkinson, C.; Jérusalem, A.; Reed, RC (2017-08-15). «О механизме микродвойникования в монокристаллическом суперсплаве». Acta Materialia . 135 : 314–329. Bibcode : 2017AcMat.135..314B. doi : 10.1016/j.actamat.2017.05.072 . hdl : 10044/1/63276 . ISSN  1359-6454. S2CID  55924981.
  47. ^ ab Махаджан, С.; Уильямс, ДФ (1973-06-01). «Деформационное двойникование в металлах и сплавах». International Metallurgical Reviews . 18 (2): 43–61. doi :10.1179/imtlr.1973.18.2.43. ISSN  0367-9020.
  48. ^ Бейерлейн, И. Дж.; Каполунго, Л.; Маршалл, П. Э.; МакКейб, Р. Дж.; Томе, К. Н. (28.05.2010). «Статистический анализ деформационного двойникования в магнии». Philosophical Magazine . 90 (16): 2161–2190. Bibcode :2010PMag...90.2161B. doi :10.1080/14786431003630835. ISSN  1478-6435. S2CID  136111937.
  49. ^ ab Lloyd, JT (2018-02-28). "Модель на основе дислокаций для роста двойников внутри и поперек зерен". Труды Королевского общества A: Математические, физические и инженерные науки . 474 (2210): 20170709. Bibcode : 2018RSPSA.47470709L . doi : 10.1098/rspa.2017.0709. PMC 5832837. PMID  29507516. 
  50. ^ Venables, JA (1961-03-01). «Деформационное двойникование в гранецентрированных кубических металлах». The Philosophical Magazine . 6 (63): 379–396. Bibcode : 1961PMag....6..379V. doi : 10.1080/14786436108235892. ISSN  0031-8086.
  51. ^ Йоханссон, Йохан; Оден, Магнус (2000-06-01). «Распределение нагрузки между аустенитом и ферритом в дуплексной нержавеющей стали во время циклической нагрузки». Metallurgical and Materials Transactions A. 31 ( 6): 1557–1570. Bibcode : 2000MMTA...31.1557J. doi : 10.1007/s11661-000-0166-3. ISSN  1543-1940. S2CID  137142133.
  52. ^ Marrow, TJ; King, JE (1994-06-15). "Механизмы распространения усталостных трещин в термически состаренной дуплексной нержавеющей стали". Materials Science and Engineering: A . 183 (1): 91–101. doi :10.1016/0921-5093(94)90893-1. ISSN  0921-5093.
  53. ^ Кристиан, Дж. В.; Махаджан, С. (1995-01-01). «Деформационное двойникование». Progress in Materials Science . 39 (1): 1–157. doi :10.1016/0079-6425(94)00007-7. ISSN  0079-6425.
  54. ^ Sleeswyk, A. W (1962-08-01). «Эмиссарные дислокации: Теория и эксперименты по распространению деформационных двойников в α-железе». Acta Metallurgica . 10 (8): 705–725. doi :10.1016/0001-6160(62)90040-8. ISSN  0001-6160.
  55. ^ Spreadborough, J.; Langheinrich, D.; Anderson, E.; Brandon, D. (декабрь 1964 г.). «Наблюдения за ямками травления, касающиеся двойников в железе и железных сплавах». Журнал прикладной физики . 35 (12): 3585–3587. Bibcode : 1964JAP....35.3585S. doi : 10.1063/1.1713275. ISSN  0021-8979.
  56. ^ Guo, Y.; Abdolvand, H.; Britton, TB; Wilkinson, AJ (2017-03-01). "Рост двойников {1122} в титане: комбинированное экспериментальное и модельное исследование локального состояния деформации". Acta Materialia . 126 : 221–235. doi : 10.1016/j.actamat.2016.12.066 . hdl : 10044/1/67478 . ISSN  1359-6454. S2CID  136128910.
  57. ^ Баксеванакис, КП; Гургиотис, ПА; Георгиадис, ХГ (июль 2017 г.). «Взаимодействие трещин с дислокациями в упругости парных напряжений. Часть I: Режим открытия». International Journal of Solids and Structures . 118–119: 179–191. doi : 10.1016/j.ijsolstr.2017.03.019 . ISSN  0020-7683. S2CID  55155535.
  58. ^ Аб Качер, Джош; Сабиш, Джулиан Э.; Минор, Эндрю М. (01 июля 2019 г.). «Статистический анализ взаимодействия двойников и границ зерен в чистом рении». Акта Материалия . 173 : 44–51. Бибкод : 2019AcMat.173...44K. дои : 10.1016/j.actamat.2019.04.051 . ISSN  1359-6454.
  59. ^ Gong, Mingyu; Hirth, John P.; Liu, Yue; Shen, Yao; Wang, Jian (2017-11-03). «Структуры интерфейса и механизмы двойникования двойников в гексагональных металлах». Materials Research Letters . 5 (7): 449–464. doi : 10.1080/21663831.2017.1336496 . S2CID  136448819.
  60. ^ Ван, Юньчжи; Ли, Цзюй (2010-02-01). «Моделирование фазового поля дефектов и деформации». Acta Materialia . 58 (4): 1212–1235. Bibcode : 2010AcMat..58.1212W. doi : 10.1016/j.actamat.2009.10.041. ISSN  1359-6454.
  61. ^ Эшелби, Джон Дуглас; Мотт, Невилл Фрэнсис (1951-11-06). «Сила, действующая на упругую сингулярность». Философские труды Лондонского королевского общества. Серия A, Математические и физические науки . 244 (877): 87–112. Bibcode : 1951RSPTA.244...87E. doi : 10.1098/rsta.1951.0016. S2CID  14703976.
  62. ^ Райс, Дж. Р. (1968-06-01). «Независимый от пути интеграл и приближенный анализ концентрации деформации надрезами и трещинами». Журнал прикладной механики . 35 (2): 379–386. Bibcode : 1968JAM....35..379R. doi : 10.1115/1.3601206. ISSN  0021-8936.
  63. ^ Venables, J. A (1964-07-01). "Электронная микроскопия деформационного двойникования". Журнал физики и химии твердого тела . 25 (7): 685–692. Bibcode :1964JPCS...25..685V. doi :10.1016/0022-3697(64)90177-5. ISSN  0022-3697.

Источники

Внешние ссылки