Смачивание

Способность жидкости поддерживать контакт с твердой поверхностью

Капли воды на ткани, которая была сделана несмачиваемой с помощью химической обработки.

Смачивание — это способность жидкости вытеснять газ для поддержания контакта с твердой поверхностью , возникающая в результате межмолекулярного взаимодействия при их сближении. ^[1] Это происходит в присутствии газообразной фазы или другой жидкой фазы, не смешивающейся с первой. Степень смачивания (смачиваемости) определяется балансом сил между адгезионными и когезионными силами . Существует два типа смачивания: нереактивное смачивание и реактивное смачивание. ^{[2] [3]}

Смачивание важно для связывания или сцепления двух материалов. ^[4] Смачивание и поверхностные силы, которые контролируют смачивание, также отвечают за другие связанные эффекты, включая капиллярные эффекты. Поверхностно-активные вещества могут использоваться для увеличения смачивающей способности жидкости, такой как вода.

Смачивание находится в центре внимания исследователей в области нанотехнологий и нанонауки в связи с появлением многих наноматериалов за последние два десятилетия (например, графен , ^[5] углеродные нанотрубки , наносетки из нитрида бора ^[6] ).

Объяснение

Рисунок 1: Угол контакта капли жидкости с твердой поверхностью

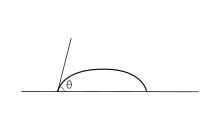
Силы адгезии между жидкостью и твердым телом заставляют каплю жидкости растекаться по поверхности. Силы когезии внутри жидкости заставляют каплю сворачиваться и избегать контакта с поверхностью.

Рисунок 2: Смачивание различных жидкостей: A показывает жидкость с очень слабым смачиванием, а C показывает жидкость с большим смачиванием. A имеет большой угол контакта, а C — малый угол контакта.

Угол контакта (θ), как показано на рисунке 1, представляет собой угол, под которым граница раздела жидкость-пар встречается с границей раздела твердое тело-жидкость. Угол контакта определяется балансом между адгезионными и когезионными силами. По мере того, как тенденция капли растекаться по плоской твердой поверхности увеличивается, угол контакта уменьшается. Таким образом, угол контакта является обратной мерой смачиваемости. ^{[7] [8]}

Угол контакта менее 90° (малый угол контакта) обычно означает, что смачивание поверхности очень благоприятно, и жидкость распределится по большой площади поверхности. Углы контакта более 90° (большой угол контакта) обычно означают, что смачивание поверхности неблагоприятно, поэтому жидкость минимизирует контакт с поверхностью и образует компактную каплю жидкости.

Для воды смачиваемая поверхность может также называться гидрофильной , а несмачиваемая поверхность — гидрофобной . Супергидрофобные поверхности имеют контактные углы более 150°, что свидетельствует о почти полном отсутствии контакта между каплей жидкости и поверхностью. Иногда это называют « эффектом лотоса ». В таблице описаны различные контактные углы и соответствующие им взаимодействия твердое тело/жидкость и жидкость/жидкость. ^[9] Для жидкостей, не являющихся водой, термин «лиофильный» используется для условий с низким контактным углом, а «лиофобный» — при более высоких контактных углах. Аналогично термины «омнифобный» и «омнифильный» применяются как к полярным , так и к неполярным жидкостям.

Поверхности с высокой и низкой энергией

Жидкости могут взаимодействовать с двумя основными типами твердых поверхностей. Традиционно твердые поверхности делятся на твердые тела с высокой и низкой энергией. Относительная энергия твердого тела связана с объемной природой самого твердого тела. Твердые тела, такие как металлы, стекла и керамика , известны как «твердые тела», потому что химические связи , которые удерживают их вместе (например, ковалентные , ионные или металлические ), очень прочны. Таким образом, требуется большое количество энергии, чтобы разрушить эти твердые тела (альтернативно, большое количество энергии требуется, чтобы разрезать объем и создать две отдельные поверхности), поэтому их называют «высокоэнергетическими». Большинство молекулярных жидкостей достигают полного смачивания с поверхностями с высокой энергией.

Другой тип твердых тел — это слабые молекулярные кристаллы (например, фторуглероды , углеводороды и т. д.), где молекулы удерживаются вместе в основном физическими силами (например, силами Ван-дер-Ваальса и водородными связями ). Поскольку эти твердые тела удерживаются вместе слабыми силами, для их разрушения требуется очень малое количество энергии, поэтому их называют «низкоэнергетическими». В зависимости от типа выбранной жидкости низкоэнергетические поверхности могут допускать как полное, так и частичное смачивание. ^{[10] [11]}

Сообщалось, что динамические поверхности подвергаются изменениям поверхностной энергии при применении соответствующих стимулов. Например, было показано, что поверхность, представляющая молекулярные моторы, управляемые фотонами, подвергается изменениям угла контакта с водой при переключении между бистабильными конформациями с различной поверхностной энергией. ^[12]

Смачивание низкоэнергетических поверхностей

Низкоэнергетические поверхности в основном взаимодействуют с жидкостями посредством дисперсионных ( ван-дер-ваальсовых ) сил. Уильям Зисман сделал несколько ключевых открытий: ^[13]

Зисман заметил, что cos θ линейно увеличивается с уменьшением поверхностного натяжения (γ _LV ) жидкости. Таким образом, он смог установить линейную функцию между cos θ и поверхностным натяжением (γ _LV ) для различных органических жидкостей.

Поверхность более смачиваемая, когда γ _LV и θ малы. Зисман назвал пересечение этих линий при cos θ = 1 критическим поверхностным натяжением (γ _c ) этой поверхности. Это критическое поверхностное натяжение является важным параметром, поскольку оно характерно только для твердого тела.

Зная критическое поверхностное натяжение твердого тела, можно предсказать смачиваемость поверхности. ^[7] Смачиваемость поверхности определяется наиболее удаленными химическими группами твердого тела. Различия в смачиваемости между поверхностями, которые имеют схожую структуру, обусловлены различиями в упаковке атомов. Например, если поверхность имеет разветвленные цепи, она будет иметь худшую упаковку, чем поверхность с прямыми цепями. Более низкое критическое поверхностное натяжение означает менее смачиваемую поверхность материала.

Идеальные твердые поверхности

Идеальная поверхность плоская, жесткая, идеально гладкая, химически однородная и имеет нулевой гистерезис угла контакта . Нулевой гистерезис подразумевает, что наступающий и отступающий углы контакта равны. Другими словами, существует только один термодинамически устойчивый угол контакта. Когда капля жидкости помещается на такую ​​поверхность, образуется характерный угол контакта, как показано на рисунке 1. Кроме того, на идеальной поверхности капля вернется к своей первоначальной форме, если ее потревожить. ^{[9] [13]} Следующие выводы применимы только к идеальным твердым поверхностям; они справедливы только для состояния, в котором интерфейсы не движутся, а линия границы фаз находится в равновесии.

Минимизация энергии, три фазы

Рисунок 3: Сосуществование трех жидких фаз во взаимном контакте; здесь α, β и θ обозначают как фазу, так и ее контактный угол.

Рисунок 4: Треугольник Неймана, связывающий поверхностные энергии и контактные углы трех жидких фаз, сосуществующих в статическом равновесии, как показано на рисунке 3.

На рисунке 3 показана линия контакта, где встречаются три фазы. В состоянии равновесия чистая сила на единицу длины, действующая вдоль линии границы между тремя фазами, должна быть равна нулю. Компоненты чистой силы в направлении вдоль каждой из границ раздела определяются как:

${\displaystyle {\begin{aligned}\gamma _{\alpha \theta }+\gamma _{\theta \beta }\cos \left(\theta \right)+\gamma _{\alpha \beta }\cos \left(\alpha \right)&=0\\\gamma _{\alpha \theta }\cos \left(\theta \right)+\gamma _{\theta \beta }+\gamma _{\alpha \beta }\cos \left(\beta \right)&=0\\\gamma _{\alpha \theta }\cos \left(\alpha \right)+\gamma _{\theta \beta }\cos \left(\beta \right)+\gamma _{\alpha \beta }&=0\end{aligned}}}$

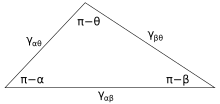
где α, β и θ — это показанные углы, а γ _ij — это поверхностная энергия между двумя указанными фазами. Эти отношения также могут быть выражены аналогом треугольника, известного как треугольник Неймана, показанного на рисунке 4. Треугольник Неймана согласуется с геометрическим ограничением, что , и применение к нему закона синусов и закона косинусов дает соотношения, которые описывают, как интерфейсные углы зависят от соотношений поверхностных энергий. ^[14] ${\displaystyle \alpha +\beta +\theta =2\pi }$

Поскольку эти три поверхностные энергии образуют стороны треугольника , они ограничены неравенствами треугольника, γ _ij < γ _jk + γ _ik, что означает, что ни одно из поверхностных натяжений не может превышать сумму двух других. Если три жидкости с поверхностными энергиями, которые не следуют этим неравенствам, приводятся в контакт, то не будет существовать равновесной конфигурации, соответствующей рисунку 3.

Упрощение до плоской геометрии, соотношение Юнга

Рисунок 5: Угол контакта капли жидкости, смоченной твердой поверхностью

Если β-фазу заменить плоской жесткой поверхностью, как показано на рисунке 5, то β = π, и второе уравнение чистой силы упрощается до уравнения Юнга, ^[15]

${\displaystyle \gamma _{SG}=\gamma _{SL}+\gamma _{LG}\cos \left(\theta \right)}$^[16]

которое связывает поверхностные натяжения между тремя фазами: твердой , жидкой и газообразной . Впоследствии это предсказывает угол контакта капли жидкости на твердой поверхности на основе знания трех задействованных поверхностных энергий. Это уравнение также применимо, если «газовая» фаза является другой жидкостью, несмешивающейся с каплей первой «жидкой» фазы.

Упрощение до плоской геометрии, соотношение Юнга, полученное из вариационного вычисления

Рассмотрим интерфейс как кривую для где - свободный параметр. Свободная энергия, которую необходимо минимизировать, равна ${\displaystyle y(x)}$ ${\displaystyle x\in I=[0,L]}$ ${\displaystyle L}$

${\displaystyle {\cal {F}}[y,L]=\int _{0}^{L}\left(\gamma _{LG}{\sqrt {1+y'^{2}}}+(\gamma _{SL}-\gamma _{SG})\right)dx}$

с ограничениями , которые мы можем записать как и фиксированный объем . ${\displaystyle y(0)=y(L)=0}$ ${\displaystyle \int _{I}y'dx=0}$ ${\displaystyle \int _{I}ydx=A}$

Таким образом, модифицированный лагранжиан с учетом ограничений имеет вид

${\displaystyle {\cal {L}}=\gamma _{LG}{\sqrt {1+y'^{2}}}+(\gamma _{SL}-\gamma _{SG})-\lambda _{1}y'-\lambda _{2}y}$

где — множители Лагранжа. По определению, импульс и гамильтониан, который вычисляется как: ${\displaystyle \lambda _{i}}$ ${\displaystyle p=\partial _{y'}{\cal {L}}}$ ${\displaystyle {\cal {H}}=py'-{\cal {L}}}$

${\displaystyle {\cal {H}}=-\gamma _{LG}{\frac {1}{\sqrt {1+y'^{2}}}}-(\gamma _{SL}-\gamma _{SG})+\lambda _{2}y}$

Теперь вспомним, что граница свободна по направлению и является свободным параметром. Поэтому мы должны иметь: ${\displaystyle x}$ ${\displaystyle L}$

${\displaystyle {\frac {\partial {\cal {F}}}{\partial L}}=-{\cal {H}}=0}$

На границе и , следовательно, мы восстанавливаем уравнение Юнга. ${\displaystyle y(L)=0}$ ${\displaystyle (1+y'^{2})^{-1/2}=\cos \theta }$

Неидеально гладкие поверхности и краевой угол Юнга

Уравнение Юнга предполагает идеально плоскую и жесткую поверхность, часто называемую идеальной поверхностью . Во многих случаях поверхности далеки от этой идеальной ситуации, и здесь рассматриваются два случая: случай шероховатых поверхностей и случай гладких поверхностей, которые все еще являются реальными (конечно жесткими). ​​Даже на идеально гладкой поверхности капля будет предполагать широкий спектр углов контакта, начиная от так называемого угла контакта при наступлении, , до так называемого угла контакта при отступлении, . Равновесный угол контакта ( ) можно рассчитать из и, как было показано Тэдмором ^[17], как, ${\displaystyle \theta _{\mathrm {A} }}$ ${\displaystyle \theta _{\mathrm {R} }}$ ${\displaystyle \theta _{\mathrm {c} }}$ ${\displaystyle \theta _{\mathrm {A} }}$ ${\displaystyle \theta _{\mathrm {R} }}$

${\displaystyle \theta _{\mathrm {c} }=\arccos \left({\frac {r_{\mathrm {A} }\cos \left(\theta _{\mathrm {A} }\right)+r_{\mathrm {R} }\cos \left(\theta _{\mathrm {R} }\right)}{r_{\mathrm {A} }+r_{\mathrm {R} }}}\right)}$

где

${\displaystyle r_{\mathrm {A} }=\left({\frac {\sin ^{3}\left(\theta _{\mathrm {A} }\right)}{2-3\cos \left(\theta _{\mathrm {A} }\right)+\cos ^{3}\left(\theta _{\mathrm {A} }\right)}}\right)^{\frac {1}{3}}~;~~r_{\mathrm {R} }=\left({\frac {\sin ^{3}\left(\theta _{\mathrm {R} }\right)}{2-3\cos \left(\theta _{\mathrm {R} }\right)+\cos ^{3}\left(\theta _{\mathrm {R} }\right)}}\right)^{\frac {1}{3}}}$

Уравнение Юнга–Дюпре и коэффициент распространения

Уравнение Юнга-Дюпре ( Томас Янг 1805; Антанас Дюпре и Поль Дюпре 1869) гласит, что ни γ _SG, ни γ _SL не могут быть больше суммы двух других поверхностных энергий. ^{[18] [19]} Следствием этого ограничения является предсказание полного смачивания, когда γ _SG > γ _SL + γ _LG , и нулевого смачивания, когда γ _SL > γ _SG + γ _LG . Отсутствие решения уравнения Юнга-Дюпре является показателем того, что для этих ситуаций не существует равновесной конфигурации с контактным углом между 0 и 180°. ^[20]

Полезным параметром для измерения смачивания является параметр распространения S ,

${\displaystyle S=\gamma _{SG}-\left(\gamma _{SL}+\gamma _{LG}\right)}$

При S > 0 жидкость смачивает поверхность полностью (полное смачивание). При S < 0 происходит частичное смачивание.

Объединение определения параметра распространения с соотношением Юнга дает уравнение Юнга–Дюпре:

${\displaystyle S=\gamma _{LG}\left(\cos \left(\theta \right)-1\right)}$

которое имеет физические решения только для θ, когда S < 0.

Обобщенная модель угла контакта капель на плоских и изогнутых поверхностях

С усовершенствованием методов измерения, таких как АСМ, конфокальная микроскопия и СЭМ, исследователи смогли производить и отображать капли во все меньших масштабах. С уменьшением размера капель появились новые экспериментальные наблюдения смачивания. Эти наблюдения подтверждают, что модифицированное уравнение Юнга ^[21] не выполняется в микро-нано масштабах. Кроме того, знак линейного натяжения не сохраняется посредством модифицированного уравнения Юнга. ^[22]

Для неподвижной капли свободная энергия трехфазной системы может быть выражена как: ^{[23] [24]}

${\displaystyle \delta w=\gamma _{LV}dA_{LV}+\gamma _{SL}dA_{SL}+\gamma _{SV}dA_{SV}-\kappa dL-PdV-VdP}$

При постоянном объеме в термодинамическом равновесии это сводится к: ^[25]

${\displaystyle 0={\frac {dA_{LG}}{dA_{SL}}}+{\frac {\gamma _{SL}-\gamma _{SG}}{\gamma _{LG}}}-{\frac {\kappa }{\gamma _{LG}}}{\frac {dL}{dA_{SL}}}-{\frac {V}{\gamma _{LG}}}{\frac {dP}{dA_{SL}}}}$

Обычно член VdP игнорируется для больших капель, однако работа VdP становится значимой в малых масштабах. Изменение давления при постоянном объеме на свободной границе жидкость-пар обусловлено давлением Лапласа , которое пропорционально средней кривизне капли и не равно нулю. Решение приведенного выше уравнения для выпуклых и вогнутых поверхностей дает: ^[26]

${\displaystyle \cos(\theta \mp \alpha )=A+B{\frac {\cos(\alpha )}{a}}\pm C\sin(\theta \mp \alpha )(\cos(\theta )+1)^{2}{\biggl (}{\frac {\sin(\alpha )(\cos(\alpha )+2)}{(\cos(\alpha )+1)^{2}}}\mp {\frac {\sin(\theta )(\cos(\theta )+2)}{(\cos(\theta )+1)^{2}}}{\biggr )}}$

Где постоянные параметры A, B и C определяются как:

Схематические диаграммы капель на плоских (а), вогнутых (б) и выпуклых (в) поверхностях ^[26]

${\displaystyle A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}}$, и ${\displaystyle B={\frac {\kappa }{\gamma _{LG}}}}$ ${\displaystyle C={\frac {\gamma }{3\gamma _{LG}}}}$

Это уравнение связывает угол контакта , геометрическое свойство сидячей капли с объемной термодинамикой, энергией на границе трехфазного контакта и кривизной поверхности α. Для особого случая сидячей капли на плоской поверхности (α=0), ${\displaystyle \theta }$

${\displaystyle \cos(\theta )={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}+{\frac {\kappa }{\gamma _{LG}}}{\frac {1}{a}}-{\frac {\gamma }{3\gamma _{LG}}}(2+\cos(\theta )-2\cos ^{2}(\theta )-\cos ^{3}(\theta ))}$

Первые два члена — это модифицированное уравнение Юнга, ^[21] , а третий член обусловлен давлением Лапласа. Это нелинейное уравнение правильно предсказывает знак и величину κ, сглаживание угла контакта в очень малых масштабах и гистерезис угла контакта. ^{[26] [22]}

Расчетное прогнозирование смачивания

Для многих конфигураций поверхность/адсорбат данные о поверхностной энергии и экспериментальные наблюдения недоступны. Поскольку смачивающие взаимодействия имеют большое значение в различных приложениях, часто желательно предсказать и сравнить поведение смачивания различных поверхностей материалов с определенными кристаллографическими ориентациями по отношению к воде или другим адсорбатам. Это можно сделать с атомистической точки зрения с помощью инструментов, включая молекулярную динамику и теорию функционала плотности . ^{[27] [28]} В теоретическом прогнозировании смачивания с помощью подходов ab initio , таких как DFT, лед обычно заменяет воду. Это связано с тем, что расчеты DFT обычно проводятся в предположении условий нулевого теплового движения атомов, по сути, означая, что моделирование проводится при абсолютном нуле . Тем не менее, это упрощение дает результаты, которые имеют отношение к адсорбции воды в реалистичных условиях, и использование льда для теоретического моделирования смачивания является обычным явлением. ^[29]

Неидеальные шероховатые твердые поверхности

Рисунок 6: Схема наступающих и отступающих контактных углов

В отличие от идеальных поверхностей, реальные поверхности не обладают идеальной гладкостью, жесткостью или химической однородностью. Такие отклонения от идеальности приводят к явлению, называемому гистерезисом угла контакта , который определяется как разница между наступающим (θ _a ) и отступающим (θ _r ) углами контакта ^[30]

${\displaystyle {\text{H}}=\,\theta _{a}-\,\theta _{r}}$

Когда угол контакта находится между случаями наступления и отступления, линия контакта считается закрепленной, и можно наблюдать гистерезисное поведение, а именно гистерезис угла контакта . Когда эти значения превышены, смещение линии контакта, такое как на рисунке 3, будет происходить либо за счет расширения, либо за счет втягивания капли. ^[31] На рисунке 6 изображены углы контакта наступления и отступления. Угол контакта наступления является максимальным устойчивым углом, тогда как угол контакта отступления является минимальным устойчивым углом. Гистерезис угла контакта возникает из-за того, что на неидеальном твердом теле обнаруживается много различных термодинамически устойчивых углов контакта. Эти изменяющиеся термодинамически устойчивые углы контакта известны как метастабильные состояния. ^[13]

Такое движение границы раздела фаз, включающее наступление и отступление контактных углов, известно как динамическое смачивание. Разница между динамическим и статическим углами смачивания пропорциональна капиллярному числу , , Когда контактная линия продвигается, покрывая большую часть поверхности жидкостью, контактный угол увеличивается и, как правило, связан со скоростью контактной линии. ^{[31] [32]} Если скорость контактной линии увеличивается без ограничений, контактный угол увеличивается, и по мере приближения к 180° газовая фаза будет увлекаться тонким слоем между жидкостью и твердым телом. Это кинетический неравновесный эффект, который возникает из-за того, что контактная линия движется с такой высокой скоростью, что полное смачивание не может произойти. ${\displaystyle Ca}$

Хорошо известное отклонение от идеальных условий происходит, когда интересующая поверхность имеет шероховатую текстуру. Шероховатая текстура поверхности может относиться к одной из двух категорий: однородная или неоднородная. Однородный режим смачивания — это когда жидкость заполняет канавки шероховатой поверхности. Однако неоднородный режим смачивания — это когда поверхность представляет собой композицию из двух типов участков. Важным примером такой составной поверхности является поверхность, состоящая из участков как воздуха, так и твердого тела. Такие поверхности оказывают различное влияние на углы контакта смачивающих жидкостей. Кэсси–Бакстер и Венцель — две основные модели, которые пытаются описать смачивание текстурированных поверхностей. Однако эти уравнения применимы только тогда, когда размер капли достаточно велик по сравнению с масштабом шероховатости поверхности. ^[33] Когда размер капли сопоставим с размером нижележащих столбов, следует учитывать эффект линейного натяжения. ^[34]

Модель Венцеля

Рисунок 7: Модель Венцеля

Модель Венцеля ^[35] описывает режим однородного смачивания, как показано на рисунке 7, и определяется следующим уравнением для угла контакта на шероховатой поверхности: ^[36]

${\displaystyle \cos \,\left(\theta ^{*}\right)=r\cos \,\left(\theta \right)}$

где — кажущийся угол контакта, который соответствует устойчивому равновесному состоянию (т.е. состоянию минимальной свободной энергии для системы). Коэффициент шероховатости, r, является мерой того, как шероховатость поверхности влияет на однородную поверхность. Коэффициент шероховатости определяется как отношение истинной площади твердой поверхности к кажущейся площади. ${\displaystyle \theta ^{*}}$

θ — это угол контакта для системы в термодинамическом равновесии, определенный для идеально плоской поверхности. Хотя уравнение Венцеля показывает, что угол контакта шероховатой поверхности отличается от собственного угла контакта, оно не описывает гистерезис угла контакта . ^[36]

Модель Кэсси–Бакстера

Рисунок 8: Модель Кэсси–Бакстера

При работе с неоднородной поверхностью модель Венцеля недостаточна. Для измерения того, как изменяется кажущийся контактный угол при взаимодействии различных материалов, необходима более сложная модель. Эта неоднородная поверхность, как показано на рисунке 8, объясняется с помощью уравнения Кэсси–Бакстера ( закон Кэсси ): ^[33]

${\displaystyle \cos \,\left(\theta ^{*}\right)=r_{f}\,f\,\cos \,\left(\theta _{\text{Y}}\right)+f-1}$

Здесь r _f — коэффициент шероховатости мокрой поверхности, а f — доля площади твердой поверхности, смоченной жидкостью. Когда f = 1 и r _f = r , уравнения Кэсси–Бакстера становятся уравнением Венцеля. С другой стороны, когда имеется много различных долей шероховатости поверхности, каждая доля общей площади поверхности обозначается как . ${\displaystyle f_{i}}$

Сумма всех равна 1 или общей поверхности. Кэсси–Бакстер также может быть преобразована в следующее уравнение: ^[37] ${\displaystyle f_{i}}$

${\displaystyle \gamma \cos \,\left(\theta ^{*}\right)=\sum _{n=1}^{N}f_{i}\left(\gamma _{\text{i,sv}}-\gamma _{\text{i,sl}}\right)}$

Здесь поверхностное натяжение Кэсси–Бакстера между жидкостью и паром, — поверхностное натяжение твердого пара каждого компонента, — поверхностное натяжение твердой жидкости каждого компонента. Стоит упомянуть случай, когда капля жидкости помещается на подложку и создает под ней небольшие воздушные карманы. Этот случай для двухкомпонентной системы обозначается как: ^[37] ${\displaystyle \gamma }$ ${\displaystyle \gamma _{i,sv}}$ ${\displaystyle \gamma _{i,sl}}$

${\displaystyle \gamma \cos \,\left(\theta ^{*}\right)=f_{1}\left(\gamma _{\text{1,sv}}-\gamma _{\text{1,sl}}\right)-\left(1-f_{1}\right)\gamma }$

Здесь ключевое отличие, на которое следует обратить внимание, заключается в том, что между твердым телом и паром нет поверхностного натяжения для второго компонента поверхностного натяжения. Это связано с предположением, что поверхность воздуха, которая подвергается воздействию, находится под каплей и является единственным другим субстратом в системе. Впоследствии уравнение затем выражается как (1 – f ). Таким образом, уравнение Кэсси можно легко вывести из уравнения Кэсси–Бакстера. Экспериментальные результаты, касающиеся свойств поверхности систем Венцеля и Кэсси–Бакстера, показали эффект закрепления для угла Юнга от 180 до 90°, области, классифицированной по модели Кэсси–Бакстера. Эта композитная система жидкость/воздух в значительной степени гидрофобна. После этой точки был обнаружен резкий переход к режиму Венцеля, где капля смачивает поверхность, но не далее краев капли. Фактически, уравнения Юнга, Венцеля и Кэсси–Бакстера представляют собой условия трансверсальности вариационной задачи смачивания. ^{[38] [39]}

Предшественник фильма

С появлением изображений высокого разрешения исследователи начали получать экспериментальные данные, которые заставили их усомниться в предположениях уравнения Кэсси–Бакстера при расчете кажущегося угла контакта. Эти группы ^{[ кто? ]} считают, что кажущийся угол контакта во многом зависит от тройной линии. Тройная линия, которая контактирует с неоднородной поверхностью, не может лежать на неоднородной поверхности, как остальная часть капли. Теоретически она должна следовать за несовершенством поверхности. Этот изгиб тройной линии неблагоприятен и не наблюдается в реальных ситуациях. Теория, которая сохраняет уравнение Кэсси–Бакстера и в то же время объясняет наличие минимизированного энергетического состояния тройной линии, основана на идее пленки-предшественника. Эта пленка субмикрометровой толщины продвигается впереди движения капли и находится вокруг тройной линии. Более того, эта пленка-предшественник позволяет тройной линии изгибаться и принимать различные конформации, которые изначально считались неблагоприятными. Эта жидкость-предшественник наблюдалась с помощью сканирующей электронной микроскопии окружающей среды (ESEM) на поверхностях с порами, сформированными в объеме. С введением концепции пленки-предшественника тройная линия может следовать энергетически возможным конформациям, тем самым правильно объясняя модель Кэсси–Бакстера. ^[40]

«Эффект лепестка» против «эффекта лотоса»

Рисунок 9: «Эффект лепестка» против «эффекта лотоса»

Внутренняя гидрофобность поверхности может быть улучшена путем текстурирования с различными масштабами длины шероховатости . Красная роза использует это преимущество, используя иерархию микро- и наноструктур на каждом лепестке, чтобы обеспечить достаточную шероховатость для супергидрофобности. Более конкретно, каждый лепесток розы имеет набор микрососочков на поверхности, а каждый сосочек, в свою очередь, имеет множество наноскладок. Термин « эффект лепестка » описывает тот факт, что капля воды на поверхности лепестка розы имеет сферическую форму, но не может скатиться, даже если лепесток перевернуть вверх дном. Капли воды сохраняют свою сферическую форму из-за супергидрофобности лепестка (угол контакта около 152,4°), но не скатываются, потому что поверхность лепестка имеет высокую силу сцепления с водой. ^[41]

При сравнении « эффекта лепестка » с « эффектом лотоса » важно отметить некоторые поразительные различия. Поверхностная структура листа лотоса и лепестка розы, как показано на рисунке 9, может быть использована для объяснения двух различных эффектов.

Лист лотоса имеет случайно шероховатую поверхность и низкий гистерезис угла контакта , что означает, что капля воды не может смочить микроструктурные пространства между шипами. Это позволяет воздуху оставаться внутри текстуры, вызывая неоднородную поверхность, состоящую как из воздуха, так и из твердого вещества. В результате сила сцепления между водой и твердой поверхностью чрезвычайно мала, что позволяет воде легко скатываться (т. е. явление « самоочищения »).

Микро- и наноструктуры лепестка розы больше по масштабу, чем у листа лотоса, что позволяет жидкой пленке пропитывать текстуру. Однако, как видно на рисунке 9, жидкость может проникать в более крупные канавки, но не может проникать в более мелкие канавки. Это известно как режим пропитывающего смачивания Кэсси. Поскольку жидкость может смачивать более крупные канавки, сила сцепления между водой и твердым телом очень высока. Это объясняет, почему капля воды не упадет, даже если лепесток наклонен под углом или перевернут вверх дном. Этот эффект не сработает, если объем капли будет больше 10 мкл, поскольку будет нарушен баланс между весом и поверхностным натяжением. ^[42]

Переход Кэсси–Бакстер в Вензель

Рисунок 10: Грибное состояние

В модели Кэсси–Бакстера капля находится на текстурированной поверхности с захваченным воздухом под ней. Во время перехода смачивания из состояния Кэсси в состояние Венцеля воздушные карманы больше не являются термодинамически стабильными, и жидкость начинает зарождаться из середины капли, создавая «грибное состояние», как показано на рисунке 10. ^[43] Условие проникновения задается следующим образом:

${\displaystyle \cos \,\left(\theta _{\text{C}}\right)={\frac {\phi -1}{r-\phi }}}$

где

• θ _C — критический угол контакта
• Φ — доля поверхности раздела твердое тело/жидкость, где капля контактирует с поверхностью
• r — шероховатость твердого тела (для плоской поверхности r = 1)

Рисунок 11: Фронт проникновения распространяется за пределы падения

Фронт проникновения распространяется, чтобы минимизировать поверхностную энергию, пока не достигнет краев капли, таким образом достигая состояния Венцеля. Поскольку твердое тело можно считать поглощающим материалом из-за шероховатости его поверхности, это явление распространения и впитывания называется полуфитингом. Контактные углы, при которых происходит распространение/впитывание, находятся в диапазоне от 0 до π/2. ^[44]

Модель Венцеля справедлива между θ _C и π/2. Если угол контакта меньше Θ _C , фронт проникновения распространяется за пределы капли и на поверхности образуется жидкая пленка. На рисунке 11 изображен переход из состояния Венцеля в состояние поверхностной пленки. Пленка сглаживает шероховатость поверхности, и модель Венцеля больше не применима. В этом состоянии условие равновесия и соотношение Юнга дают:

${\displaystyle \cos \,\left(\theta ^{*}\right)=\phi \cos \,\left(\theta _{C}\right)+\left(1-\phi \right)}$^[43]

Тонко настраивая шероховатость поверхности, можно добиться перехода как между супергидрофобными, так и супергидрофильными областями. Как правило, чем шероховатее поверхность, тем она более гидрофобна.

Динамика распространения

Если капля помещена на гладкую горизонтальную поверхность, она, как правило, не находится в состоянии равновесия. Следовательно, она распространяется до тех пор, пока не будет достигнут радиус равновесного контакта (частичное смачивание). Принимая во внимание капиллярные, гравитационные и вязкие вклады, радиус капли как функцию времени можно выразить как ^[45]

${\displaystyle r(t)=r_{e}\left[1-\exp \left(-\left({\frac {2\gamma _{LG}}{r_{e}^{12}}}+{\frac {\rho g}{9r_{e}^{10}}}\right){\frac {24\lambda V^{4}\left(t+t_{0}\right)}{\pi ^{2}\eta }}\right)\right]^{\frac {1}{6}}.}$

Для ситуации полного смачивания радиус капли в любой момент процесса распространения определяется выражением

${\displaystyle r(t)=\left[\left(\gamma _{LG}{\frac {96\lambda V^{4}}{\pi ^{2}\eta }}\left(t+t_{0}\right)\right)^{\frac {1}{2}}+\left({\frac {\lambda (t+t_{0})}{\eta }}\right)^{\frac {2}{3}}{\frac {24\rho gV^{\frac {3}{8}}}{7\cdot 96^{\frac {1}{3}}\pi ^{\frac {4}{3}}\gamma _{LG}^{\frac {1}{3}}}}\right]^{\frac {1}{6}},}$

где

• γ _LG — поверхностное натяжение жидкости
• V — объем капли
• η — вязкость жидкости
• ρ — плотность жидкости
• g — гравитационная постоянная
• λ — коэффициент формы, 37,1  м ⁻¹
• t ₀ — экспериментальное время задержки
• r _e — радиус капли в равновесии

Изменение смачивающих свойств

Поверхностно-активные вещества

Многие технологические процессы требуют контроля за распространением жидкости по твердым поверхностям. Когда капля помещается на поверхность, она может полностью смочить, частично смочить или не смочить поверхность. Уменьшая поверхностное натяжение с помощью поверхностно-активных веществ , можно сделать несмачивающий материал частично или полностью смачивающим. Избыточная свободная энергия (σ) капли на твердой поверхности равна: ^[46]

${\displaystyle \sigma =\gamma S+PV+\pi \,R^{2}\left(\gamma _{\text{SL}}-\gamma _{\text{SV}}\right)}$

• γ – поверхностное натяжение на границе раздела жидкость–пар
• γ _SL – поверхностное натяжение на границе твердого тела и жидкости
• γ _SV – поверхностное натяжение на границе раздела твердое тело–пар
• S — площадь поверхности раздела жидкость–пар
• P — избыточное давление внутри жидкости
• R — радиус основания капли

На основании этого уравнения, избыточная свободная энергия минимизируется, когда γ уменьшается, γ _SL уменьшается или γ _SV увеличивается. Поверхностно-активные вещества абсорбируются на поверхностях раздела жидкость-пар, твердое тело-жидкость и твердое тело-пар, что изменяет смачивающее поведение гидрофобных материалов для уменьшения свободной энергии. Когда поверхностно-активные вещества абсорбируются на гидрофобной поверхности, полярные головные группы обращены в раствор, а хвост направлен наружу. На более гидрофобных поверхностях поверхностно-активные вещества могут образовывать бислой на твердом теле, заставляя его становиться более гидрофильным. Динамический радиус капли можно охарактеризовать, когда капля начинает растекаться. Таким образом, контактный угол изменяется на основе следующего уравнения: ^[46]

${\displaystyle \cos \,\left(\theta (t)\right)=\cos \,\left(\theta _{0}\right)+\left(\cos \,\left(\theta _{\infty }\right)-\cos \,\left(\theta _{0}\right)\right)\left(1-\mathrm {e} ^{-{\frac {t}{\tau }}}\right)}$

• θ ₀ — начальный угол контакта
• θ _∞ — конечный угол контакта
• τ — масштаб времени переноса поверхностно-активного вещества

По мере абсорбции поверхностно-активных веществ поверхностное натяжение твердое тело-пар увеличивается, а края капли становятся гидрофильными. В результате капля растекается.

Изменения поверхности

Нити незаряженного ферроцензамещенного полимера привязаны к гидрофобной поверхности кремния . Окисление ферроценильных групп создает гидрофильную поверхность из-за электростатического притяжения между полученными зарядами и полярным растворителем. ^[47]

Ферроцен — это окислительно-восстановительно -активное металлоорганическое соединение ^[48] , которое может быть включено в различные мономеры и использовано для получения полимеров , которые могут быть привязаны к поверхности. ^[47] Винилферроцен (ферроценилэтен) может быть получен с помощью реакции Виттига ^[49] , а затем полимеризован с образованием поливинилферроцена (ПВФ), аналога полистирола . Другим полимером, который может быть образован, является поли( 2-(метакрилоилокси) этилферроценкарбоксилат), PFcMA. Как PVFc, так и PFcMA были привязаны к кремниевым пластинам, и смачиваемость была измерена, когда полимерные цепи не заряжены, а ферроценовые фрагменты окисляются с образованием положительно заряженных групп, как показано справа. ^[47] Угол контакта с водой на пластинах, покрытых PFcMA, был на 70° меньше после окисления, тогда как в случае PVFc уменьшение составило 30°, и было показано, что переключение смачиваемости обратимо. В случае PFcMA было исследовано влияние более длинных цепей с большим количеством ферроценовых групп (а также большей молярной массой ), и было обнаружено, что более длинные цепи вызывают значительно большее уменьшение угла контакта. ^{[47] [50]}

Вакансии кислорода

Оксиды редкоземельных элементов проявляют внутреннюю гидрофобность и, следовательно, могут использоваться в термостойких теплообменниках и других приложениях, связанных с гидрофобностью при высоких температурах. ^[51] Наличие кислородных вакансий на поверхностях церия или других оксидов редкоземельных элементов играет важную роль в управлении смачиваемостью поверхности. Адсорбция воды на поверхностях оксидов может происходить как молекулярная адсорбция, при которой молекулы H2O _{остаются} нетронутыми на конечной поверхности, или как диссоциативная адсорбция , при которой OH и H адсорбируются отдельно ^[52] на твердых поверхностях. Обычно обнаруживается, что наличие кислородных вакансий усиливает гидрофобность, одновременно способствуя диссоциативной адсорбции. ^[53]

Смотрите также

• Адсорбция  – явление поверхностной адгезии
• тест Амотта
• Антизапотевающие вещества  – химические вещества, которые предотвращают конденсацию воды в виде мелких капелек на поверхности.
• Вымывание  – отвод жидкости от поверхности, которую она вынуждена покрыть.
• Электросмачивание
• Плавучесть  – сила, направленная вверх и противодействующая весу объекта, погруженного в жидкость.Pages displaying short descriptions of redirect targets
• Метод лежащей капли  – Метод определения поверхностной энергии твердого тела
• Мыльный пузырь  – Тонкая пленка мыльной воды, содержащая воздух.
• Подъем в ядре  – Лабораторная техника
• Ток смачивания  – минимальный электрический ток через контакт, необходимый для преодоления сопротивления поверхностной пленки.
• Напряжение смачивания  – минимальный электрический ток через контакт, необходимый для преодоления сопротивления поверхностной пленки.Pages displaying short descriptions of redirect targets
• Индекс смачиваемости лака
• Индекс смачиваемости USBM

Ссылки

1. Кэрролл, Грегори Т.; Турро, Николас Дж.; Маммана, Анджела; Коберштейн, Джеффри Т. (2017). «Фотохимическая иммобилизация полимеров на поверхности: управление толщиной пленки и смачиваемостью». Фотохимия и фотобиология . 93 (5): 1165–1169. doi :10.1111/php.12751. ISSN  0031-8655. PMID  28295380.
2. Dezellus, O.; Eustathopoulos, N. (2010). "Фундаментальные вопросы реактивного смачивания жидкими металлами" (PDF) . Журнал материаловедения . 45 (16): 4256–4264. Bibcode :2010JMatS..45.4256D. doi :10.1007/s10853-009-4128-x. S2CID  4512480.
3. Ху, Хань; Цзи, Хай-Фэн; Сан, Ин (2013). «Влияние кислородных вакансий на смачиваемость водой поверхности ZnO». Физическая химия Химическая физика . 15 (39): 16557–65. Bibcode :2013PCCP...1516557H. doi :10.1039/C3CP51848E. PMID  23949186. S2CID  205850095.
4. Амзиан, Софиан; Колле, Флоренция (2017-03-05). Строительные материалы на основе биозаполнителей: современный отчет Технического комитета RILEM 236-BBM. Springer. ISBN 9789402410310.
5. Рафи, Дж.; Ми, Х.; Гуллапалли, Х.; Томас, А.В.; Явари, Ф.; Ши, Ю.; Аджаян, премьер-министр; Кораткар, Н.А. (2012). «Смачивающая прозрачность графена» (PDF) . Природные материалы . 11 (3): 217–22. Бибкод : 2012NatMa..11..217R. дои : 10.1038/nmat3228. PMID  22266468. Архивировано из оригинала (PDF) 15 ноября 2017 г.
6. Mertens, Stijn FL; Hemmi, Adrian; Muff, Stefan; Gröning, Oliver; De Feyter, Steven; Osterwalder, Jürg; Greber, Thomas (2016). «Переключение клейкости и адгезии жидкости на твердом теле» (PDF) . Nature . 534 (7609): 676–679. Bibcode :2016Natur.534..676M. doi :10.1038/nature18275. PMID  27357755. S2CID  205249367. Архивировано из оригинала (PDF) 2019-04-11.
7. Шарфрин, Э.; Зисман, Уильям А. (1960). «Основные соотношения в смачивании низкоэнергетических поверхностей и теория метода ретракции при получении монослоев». Журнал физической химии . 64 (5): 519–524. doi :10.1021/j100834a002.
8. Мантанис, GI; Янг, RA (1997). «Смачивание древесины». Wood Science and Technology . 31 (5): 339–353. doi :10.1007/BF01159153. ISSN  0043-7719.
9. Eustathopoulos, N.; Nicholas, MG; Drevet B. (1999). Смачиваемость при высоких температурах . Оксфорд, Великобритания: Pergamon. ISBN 978-0-08-042146-9.
10. Шрадер, М.Е.; Лёб, Г.И. (1992). Современные подходы к смачиваемости. Теория и приложения . Нью-Йорк: Plenum Press. ISBN 978-0-306-43985-8.
11. de Gennes, PG (1985). "Смачивание: статика и динамика" (PDF) . Reviews of Modern Physics . 57 (3): 827–863. Bibcode :1985RvMP...57..827D. doi :10.1103/RevModPhys.57.827. Архивировано из оригинала (PDF) 2016-09-10.
12. Чен, Куанг-Йен; Иващенко, Алексей; Кэрролл, Грегори Т.; Робертус, Джорт; Кистемакер, Йос CM; Лондон, Габор; Браун, Уэсли Р.; Рудольф, Петра; Феринга, Бен Л. (2014). «Контроль смачиваемости поверхности с помощью трехполюсных молекулярных моторов, активируемых светом». Журнал Американского химического общества . 136 (8): 3219–3224. doi :10.1021/ja412110t. PMID  24490770. S2CID  207106544.
13. Джонсон, Рулон Э. (1993) в Смачиваемость Ред. Берг, Джон. К. Нью-Йорк, Нью-Йорк: Marcel Dekker, Inc. ISBN 0-8247-9046-4 
14. Роулинсон, Дж. С.; Видом, Б. (1982). Молекулярная теория капиллярности . Оксфорд, Великобритания: Clarendon Press. ISBN 978-0-19-855642-8.
15. Янг, Т. (1805). «Очерк о сцеплении жидкостей» (PDF) . Philosophical Transactions of the Royal Society of London . 95 : 65–87. doi :10.1098/rstl.1805.0005. S2CID  116124581.
16. TS Chow (1998). "Смачивание шероховатых поверхностей". Journal of Physics: Condensed Matter . 10 (27): L445–L451. Bibcode : 1998JPCM...10L.445C. doi : 10.1088/0953-8984/10/27/001. S2CID  250874015.
17. Тадмор, Рафаэль (2004). «Энергия линии и соотношение между наступающим, отступающим и контактным углами Юнга». Ленгмюр . 20 (18): 7659–64. doi :10.1021/la049410h. PMID  15323516.
18. Шрейдер, Малкольм Э. (1995). «Янг-Дюпре снова». Ленгмюр . 11 (9): 3585–3589. doi :10.1021/la00009a049.
19. Атанас М. Дюпре, Поль Дюпре (1 января 1869 г.). Théorie mécanique de la chaleur (на французском языке). Готье-Виллар.
20. Клегг, Карл (2016). «Коэффициент распространения угла контакта». www.ramehart.com . ramé-hart . Получено 6 января 2016 г. .
21. Gibbs, Josiah Willard Auteur du texte (1928). Собрание сочинений / JW Gibbs,...
22. Wciślik, Sylwia; Mukherjee, Sayantan (июнь 2022 г.). «Оценка трех методов измерения статического угла контакта для капель наножидкости TiO 2 во время испарения». Physics of Fluids . 34 (6): 062006. Bibcode :2022PhFl...34f2006W. doi : 10.1063/5.0096644 . ISSN  1070-6631. S2CID  249715372.
23. Мармур, Абрахам (февраль 1997 г.). «Линейное натяжение и внутренний угол контакта в системах твердое тело–жидкость–жидкость». Журнал коллоидной и интерфейсной науки . 186 (2): 462–466. Bibcode : 1997JCIS..186..462M. doi : 10.1006/jcis.1996.4666. PMID  9056376.
24. Тадмор, Рафаэль (2004-08-01). «Энергия линии и связь между углами наступления, отступления и углами контакта молодых». Ленгмюр . 20 (18): 7659–7664. doi :10.1021/la049410h. ISSN  0743-7463. PMID  15323516.
25. Джаспер, Уоррен Дж.; Расипурам, Шринивасан (декабрь 2017 г.). «Соотношение между углом контакта и радиусом линии контакта для масляных капель размером от микро до [10−6 до 10−18] литра». Журнал молекулярных жидкостей . 248 : 920–926. doi :10.1016/j.molliq.2017.10.134.
26. Джаспер, Уоррен Дж.; Ананд, Надиш (май 2019 г.). «Обобщенный вариационный подход для прогнозирования контактных углов сидячих нанокапель на плоских и изогнутых поверхностях». Журнал молекулярных жидкостей . 281 : 196–203. doi :10.1016/j.molliq.2019.02.039. S2CID  104412970.
27. Сан, Сюэгуй (2017). «Моделирование молекулярной динамики смачивания Li на поверхностях W». Fusion Engineering and Design . 117 : 188–193. doi :10.1016/j.fusengdes.2016.06.037.
28. Коста, Д. (2017). «Эффекты смачивания краев носителей γ-Al2O3 и анатаз-TiO2 активными фазами MoS2 и CoMoS: исследование DFT». Журнал катализа . 246 (2): 325–334. doi :10.1016/j.jcat.2006.12.007.
29. Гидрофобность плоскостей CeO2 с низким индексом, Applied Surface Science, Elsevier, 2019, 478, стр. 68-74. в открытых архивах HAL
30. Роберт Дж. Гуд (1992). «Контактный угол, смачивание и адгезия: критический обзор». Журнал науки и технологии адгезии . 6 (12): 1269–1302. doi :10.1163/156856192X00629.
31. Shi, Z.; et al. (2018). «Динамический гистерезис угла контакта в жидких мостиках». Colloids and Surfaces A. 555 : 365–371. arXiv : 1712.04703 . doi : 10.1016/j.colsurfa.2018.07.004. S2CID  51916594.
32. De Gennes, PG (1994). Программные интерфейсы . Кембридж, Великобритания: Cambridge University Press. ISBN 978-0-521-56417-5.
33. Abraham Marmur (2003). «Смачивание гидрофобных шероховатых поверхностей: быть гетерогенным или не быть». Langmuir . 19 (20): 8343–8348. doi :10.1021/la0344682.
34. Чэнь, Сюэмэй; Ма, Жуйюань; Ли, Цзиньтао; Хао, Чунлей; Го, Вэй; Лук, БЛ; Ли, Шуай Чэн; Яо, Шухуай; Ван, Цзуанькай (2012). «Испарение капель на супергидрофобных поверхностях: шероховатость поверхности и эффекты размера малых капель» (PDF) . Physical Review Letters . 109 (11): 116101(1–6). Bibcode : 2012PhRvL.109k6101C. doi : 10.1103/PhysRevLett.109.116101. PMID  23005650. S2CID  29794436. Архивировано из оригинала (PDF) 2019-04-11.
35. Венцель, Роберт Н. «Сопротивление твердых поверхностей смачиванию водой». Промышленная и инженерная химия 28.8 (1936): 988-994.
36. де Женн, Пьер-Жиль; Брошар-Вайарт, Франсуаза; Кере, Дэвид (2004). Капиллярность и явления смачивания. Спрингер Нью-Йорк. doi: 10.1007/978-0-387-21656-0. ISBN 978-1-4419-1833-8. S2CID 137894832
37. Whyman, G.; Bormashenko, Edward; Stein, Tamir (2008). «Строгий вывод уравнений Юнга, Кэсси–Бакстера и Венцеля и анализ явления гистерезиса угла контакта». Chemical Physics Letters . 450 (4–6): 355–359. Bibcode :2008CPL...450..355W. doi :10.1016/j.cplett.2007.11.033.
38. Бормашенко, Эдвард (2009-08-05). "Уравнения Янга, Борувки–Неймана, Венцеля и Кэсси–Бакстера как условия трансверсальности для вариационной задачи смачивания". Коллоиды и поверхности A: физико-химические и инженерные аспекты . 345 (1): 163–165. doi :10.1016/j.colsurfa.2009.04.054. ISSN  0927-7757.
39. Бормашенко, Эдвард (17.01.2020). «Вариационная структура для определения контактных углов: общий термодинамический подход». Журнал «Наука и технологии адгезии» . 34 (2): 219–230. doi : 10.1080/01694243.2019.1663030. ISSN  0169-4243. S2CID  203537637.
40. Бормашенко, Е. (2008). «Почему применяется уравнение Кэсси–Бакстера?». Коллоиды и поверхности A. 324 ( 1–3): 47–50. doi :10.1016/j.colsurfa.2008.03.025.
41. Линь, Ф.; Чжан, И; Си, Дж; Чжу, И; Ван, Н; Ся, Ф; Цзян, Л (2008). «Эффект лепестка: супергидрофобное состояние с высокой силой сцепления». Langmuir . 24 (8): 4114–4119. doi :10.1021/la703821h. PMID  18312016.
42. Muzammil, I.; Li, YP; Li, XY; Lei, MK (2018). «Зависящая от рабочего цикла химическая структура и смачиваемость сополимеров акриловой кислоты и октафторциклобутана, полученных с помощью импульсной плазмы RF». Applied Surface Science . 436 : 411–418. Bibcode :2018ApSS..436..411M. doi :10.1016/j.apsusc.2017.11.261.
43. Ishino, C.; Okumura, K (2008). "Wetting transitions on textured hydrophilic surfaces" (PDF) . European Physical Journal . 25 (4): 415–424. Bibcode :2008EPJE...25..415I. doi :10.1140/epje/i2007-10308-y. PMID  18431542. S2CID  35973585. Архивировано из оригинала (PDF) 2019-04-11.
44. Quere, D.; Thiele, Uwe; Quéré, David (2008). "Смачивание текстурированных поверхностей" (PDF) . Colloids and Surfaces A . 206 (1–3): 41–46. doi :10.1016/S0927-7757(02)00061-4. Архивировано из оригинала (PDF) 2012-05-27 . Получено 2011-12-17 .
45. Харт, Михаэль; Шуберт, Дирк В. (2012). «Простой подход к динамике распространения полимерных жидкостей». Macromolecular Chemistry and Physics . 213 (6): 654–665. doi :10.1002/macp.201100631.
46. Lee, KS; Ivanova, N.; Starov, VM; Hilal, N.; Dutschk, V. (2008). "Кинетика смачивания и распространения водными растворами поверхностно-активных веществ". Advances in Colloid and Interface Science . 144 (1–2): 54–65. doi :10.1016/j.cis.2008.08.005. PMID  18834966.
47. Pietschnig, R. (2016). «Полимеры с подвесными ферроценами». Chemical Society Reviews . 45 (19): 5216–5231. doi : 10.1039/C6CS00196C . PMID  27156979.
48. Connelly, NG; Geiger, WE (1996). «Химические окислительно-восстановительные агенты для металлоорганической химии» (PDF) . Chemical Reviews . 96 (2): 877–910. doi :10.1021/cr940053x. PMID  11848774. Архивировано из оригинала (PDF) 22.01.2016.
49. Liu, W.-Y.; Xu, Q.-H.; Ma, Y.-X.; Liang, Y.-M.; Dong, N.-L.; Guan, D.-P. (2001). «Синтез производных ферроценилэтена без растворителя». Журнал металлоорганической химии . 625 : 128–132. doi :10.1016/S0022-328X(00)00927-X.
50. Элберт, Дж.; Галлей, М.; Рюттигер, К.; Брунсен, А.; Дидзолейт, Х.; Штюн, Б.; Рехан, М. (2013). «Ферроценовые полимеры для переключаемой поверхностной смачиваемости». Organometallics . 32 (20): 5873–5878. doi :10.1021/om400468p.
51. Кемсли, Джиллиан (28 января 2013 г.). «Оксиды редкоземельных элементов по своей природе гидрофобны». Новости химии и машиностроения . 91 (4).
52. Фронзи, Марко; Ассади, М. Хусейн Н.; Ханаор, Дориан А.Х.; Ханаор, Дориан А.Х.; Ган, Исян (2019). «Теоретическое понимание гидрофобности поверхностей CeO ₂ с низким индексом ». Прикладная наука о поверхности . 478 : 68–74. arXiv : 1902.02662 . Бибкод : 2019ApSS..478...68F. дои : 10.1016/j.apsusc.2019.01.208. S2CID  118895100.
53. Saini, CP; Barman, A.; Das, D.; Satpati, B.; Bhattacharyya, SR; Kanjilal, D.; Ponomaryov, A.; Zvyagin, S.; Kanjilal, A. (2017). «Роль кислородной вакансии в гидрофобном поведении наностержней TiO ₂ на химически протравленных кремниевых пирамидах». Журнал физической химии C. 121 : 278–283. doi :10.1021/acs.jpcc.6b08991.

Дальнейшее чтение

• де Женн, Пьер-Жиль; Брошар-Вайарт, Франсуаза; Кере, Дэвид (2004). Капиллярность и явления смачивания . Спрингер Нью-Йорк. дои : 10.1007/978-0-387-21656-0. ISBN 978-1-4419-1833-8. S2CID  137894832.
• Виктор М. Старов; Мануэль Г. Веларде ; Клейтон Дж. Радке (2 апреля 2007 г.). Динамика смачивания и распространения. CRC Press. ISBN 978-1-4200-1617-8.

Внешние ссылки

• Что такое смачиваемость?
• Медиа, связанные с Wetting на Wikimedia Commons