Гиперкуб

Выпуклый многогранник, n-мерный аналог квадрата и куба.

В геометрии гиперкуб — ​​это n -мерный аналог квадрата ( n = 2 ) и куба ( n = 3 ). Это замкнутая , компактная , выпуклая фигура, 1- скелет которой состоит из групп противоположных параллельных отрезков , выровненных в каждом из измерений пространства , перпендикулярных друг другу и одинаковой длины. Самая длинная диагональ единичного гиперкуба в n измерениях равна . ${\displaystyle {\sqrt {n}}}$

n - мерный гиперкуб чаще называют n -кубом или иногда n -мерным кубом . ^{[ нужна цитата ]} Термин «многогранник с мерой» (родом из Elte, 1912) ^[1] также используется, особенно в работе HSM Coxeter , который также называет гиперкубы многогранниками γ n . ^[2]

Гиперкуб — ​​это частный случай гиперпрямоугольника ( также называемого n-ортотопом ).

Единичный гиперкуб — ​​это гиперкуб, длина стороны которого равна одной единице . Часто гиперкуб, углами (или вершинами ) которого являются 2 ⁿ точек в R ⁿ с каждой координатой, равной 0 или 1, называется единичным гиперкубом.

Строительство

Диаграмма, показывающая, как создать тессеракт из точки.

Анимация, показывающая, как создать тессеракт из точки.

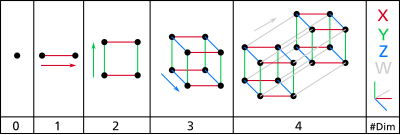
Гиперкуб можно определить, увеличивая количество измерений фигуры:

0 – Точка – это гиперкуб нулевой размерности.

1 – Если переместить эту точку на одну единицу длины, она выметет отрезок линии, который представляет собой единичный гиперкуб размерности один.

2 – Если переместить этот отрезок, его длину перпендикулярно самому себе; он выметает двумерный квадрат.

3. Если переместить квадрат на одну единицу длины в направлении, перпендикулярном плоскости, на которой он лежит, получится трехмерный куб.

4. Если переместить куб на одну единицу длины в четвертое измерение, образуется четырехмерный единичный гиперкуб (единичный тессеракт ).

Это можно обобщить на любое количество измерений. Этот процесс выметания объемов можно формализовать математически как сумму Минковского : d -мерный гиперкуб представляет собой сумму Минковского d взаимно перпендикулярных отрезков единичной длины и, следовательно, является примером зонотопа .

1- скелет гиперкуба представляет собой граф гиперкуба .

Координаты вершины

Проекция вращающегося тессеракта .

Единичный гиперкуб размерности — это выпуклая оболочка всех точек, декартовы координаты которых равны либо или . Этот гиперкуб также является декартовым произведением копий единичного интервала . Из этого путем перевода можно получить еще один единичный гиперкуб с центром в начале окружающего пространства . Это выпуклая оболочка точек, векторы декартовых координат которых равны ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle 0}$ ${\displaystyle 1}$ ${\displaystyle [0,1]^{n}}$ ${\displaystyle n}$ ${\displaystyle [0,1]}$

${\displaystyle \left(\pm {\frac {1}{2}},\pm {\frac {1}{2}},\cdots ,\pm {\frac {1}{2}}\right)\!\!.}$

Здесь символ означает, что каждая координата либо равна, либо равна . Этот единичный гиперкуб также является декартовым произведением . Любой единичный гиперкуб имеет длину ребра и -мерный объем . ${\displaystyle \pm }$ ${\displaystyle 1/2}$ ${\displaystyle -1/2}$ ${\displaystyle [-1/2,1/2]^{n}}$ ${\displaystyle 1}$ ${\displaystyle n}$ ${\displaystyle 1}$

-мерный гиперкуб, полученный как выпуклая оболочка точек с координатами или, что то же самое, как декартово произведение, также часто рассматривается из-за более простой формы координат его вершин. Длина его ребра равна , а его -мерный объем равен . ${\displaystyle n}$ ${\displaystyle (\pm 1,\pm 1,\cdots ,\pm 1)}$ ${\displaystyle [-1,1]^{n}}$ ${\displaystyle 2}$ ${\displaystyle n}$ ${\displaystyle 2^{n}}$

Лица

Каждый гиперкуб допускает в качестве своих граней гиперкубы более низкой размерности, содержащиеся в его границе. Гиперкуб измерения допускает фасеты или грани измерения : ( -мерный) отрезок имеет конечные точки; ( -мерный) квадрат имеет стороны или края; -мерный куб имеет квадратные грани; ( -мерный) тессеракт имеет в качестве граней трехмерные кубы. Число вершин гиперкуба размерностью равно ( например , у обычного -мерного куба есть вершины). ${\displaystyle n}$ ${\displaystyle 2n}$ ${\displaystyle n-1}$ ${\displaystyle 1}$ ${\displaystyle 2}$ ${\displaystyle 2}$ ${\displaystyle 4}$ ${\displaystyle 3}$ ${\displaystyle 6}$ ${\displaystyle 4}$ ${\displaystyle 8}$ ${\displaystyle n}$ ${\displaystyle 2^{n}}$ ${\displaystyle 3}$ ${\displaystyle 2^{3}=8}$

Число -мерных гиперкубов (далее называемых -кубами), содержащихся на границе -куба, равно ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle n}$

${\displaystyle E_{m,n}=2^{n-m}{n \choose m}}$, [ ^3]     где и обозначает факториал . ${\displaystyle {n \choose m}={\frac {n!}{m!\,(n-m)!}}}$ ${\displaystyle n!}$ ${\displaystyle n}$

Расширенный f-вектор для n -куба может быть вычислен как (2, 1 ) ⁿ , как и коэффициенты полиномиальных произведений . Например, тессеракт — это (2, 1 ) ⁴ = (4, 1 ) ² = (16,32,24,8, 1 ).

Например, граница -куба ( ) содержит кубы ( -cubes), квадраты ( -cubes), отрезки линий ( -cubes) и вершины ( -cubes). Это тождество можно доказать с помощью простого комбинаторного рассуждения: для каждой вершины гиперкуба существует способ выбрать набор ребер, инцидентных этой вершине. Каждый из этих наборов определяет одну из -мерных граней, инцидентных рассматриваемой вершине. Делая это для всех вершин гиперкуба, каждая из -мерных граней гиперкуба подсчитывается раз, так как в ней столько вершин, и нам нужно разделить на это число. ${\displaystyle 4}$ ${\displaystyle n=4}$ ${\displaystyle 8}$ ${\displaystyle 3}$ ${\displaystyle 24}$ ${\displaystyle 2}$ ${\displaystyle 32}$ ${\displaystyle 1}$ ${\displaystyle 16}$ ${\displaystyle 0}$ ${\displaystyle 2^{n}}$ ${\displaystyle {\tbinom {n}{m}}}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle 2^{m}}$ ${\displaystyle 2^{n}{\tbinom {n}{m}}}$

Число граней гиперкуба можно использовать для вычисления -мерного объема его границы: этот объем умножен на объем -мерного гиперкуба; то есть где – длина ребер гиперкуба. ${\displaystyle (n-1)}$ ${\displaystyle 2n}$ ${\displaystyle (n-1)}$ ${\displaystyle 2ns^{n-1}}$ ${\displaystyle s}$

Эти числа также могут быть сгенерированы с помощью линейного рекуррентного соотношения

${\displaystyle E_{m,n}=2E_{m,n-1}+E_{m-1,n-1}\!}$, с , и когда , , или . ${\displaystyle E_{0,0}=1}$ ${\displaystyle E_{m,n}=0}$ ${\displaystyle n<m}$ ${\displaystyle n<0}$ ${\displaystyle m<0}$

Например, расширение квадрата через его 4 вершины добавляет один дополнительный сегмент линии (ребро) на каждую вершину. Добавление противоположного квадрата для формирования куба образует сегменты линий. ${\displaystyle E_{1,3}=12}$

Графики

n -куб можно спроектировать внутри правильного 2- угольного многоугольника с помощью косой ортогональной проекции , показанной здесь, от отрезка прямой к 16-кубу.

Родственные семейства многогранников

Гиперкубы — одно из немногих семейств правильных многогранников , которые представлены в любом количестве измерений.

Семейство гиперкубов (смещений) — одно из трех семейств правильных многогранников , обозначенных Коксетером как γ _n . Два других — это двойственное семейство гиперкуба, кросс-многогранники , помеченные как β _n, и симплексы , помеченные как α _n . Четвертое семейство, бесконечные мозаики гиперкубов , он обозначил _как δn .

Другое родственное семейство полуправильных и однородных многогранников — это полугиперкубы , которые состоят из гиперкубов с удаленными альтернативными вершинами и добавленными в промежутках симплексными гранями, обозначенными как hγ _n .

n -кубы можно комбинировать с их двойниками ( перекрестными многогранниками ) для образования составных многогранников:

• В двух измерениях мы получаем октаграммную фигуру звезды {8/2},
• В трёх измерениях получаем соединение куба и октаэдра ,
• В четырех измерениях мы получаем соединение тессеракта и 16-клеточного .

Связь с ( n −1)-симплексами

Граф ребер n -гиперкуба изоморфен диаграмме Хассе решетки граней ( n − 1) -симплекса . В этом можно убедиться, ориентируя n -гиперкуб так, чтобы две противоположные вершины лежали вертикально, что соответствует самому ( n -1)-симплексу и нулевому многограннику соответственно. Каждая вершина, соединенная с верхней вершиной, затем однозначно отображается в одну из граней ( n -1)-симплекса ( n -2 граней), а каждая вершина, соединенная с этими вершинами, отображается в одну из n -3 граней симплекса и т. д. , а вершины, соединенные с нижней вершиной, сопоставляются с вершинами симплекса.

Это соотношение можно использовать для эффективного создания решетки граней ( n -1)-симплекса, поскольку алгоритмы перечисления решетки граней, применимые к общим многогранникам, являются более дорогостоящими в вычислительном отношении.

Обобщенные гиперкубы

Регулярные комплексные многогранники могут быть определены в комплексном гильбертовом пространстве , называемом обобщенными гиперкубами , γ^п
_н= _p {4} ₂ {3}... ₂ {3} ₂ , или... Действительные решения существуют при p = 2, т.е. γ²
_н= γ _n = ₂ {4} ₂ {3}... ₂ {3} ₂ = {4,3,..,3}. При p > 2 они существуют в . Фасеты представляют собой обобщенный ( n −1)-куб, а вершинная фигура — регулярные симплексы . ${\displaystyle \mathbb {C} ^{n}}$

Периметр правильного многоугольника , видимый в этих ортогональных проекциях, называется многоугольником Петри . Обобщенные квадраты ( n = 2) показаны с краями, обведенными p -ребрами чередующегося красного и синего цвета, тогда как более высокие n -кубы нарисованы с p -ребрами, обведенными черным.

Число m -гранных элементов в p -обобщенном n -кубе равно: . Это p ⁿ вершин и pn граней. ^[5] ${\displaystyle p^{n-m}{n \choose m}}$

Отношение к возведению в степень

Любое положительное целое число, возведенное в другую положительную целую степень, даст третье целое число, причем это третье целое число представляет собой определенный тип фигурного числа , соответствующий n -кубу с числом измерений, соответствующим экспоненте. Например, показатель степени 2 даст квадратное число или «идеальный квадрат», который можно расположить в форме квадрата с длиной стороны, соответствующей длине стороны. Точно так же показатель степени 3 даст идеальный куб — ​​целое число, которое можно расположить в форме куба с длиной стороны, равной основанию. В результате действие возведения числа до 2 или 3 чаще называют « возведением в квадрат » и «возведением в куб» соответственно. Однако названия гиперкубов более высокого порядка, похоже, не широко используются высшими силами.

Смотрите также

• Математический портал

• Сеть взаимосвязей гиперкуба компьютерной архитектуры
• Гипероктаэдрическая группа , группа симметрии гиперкуба.
• Гиперсфера
• Симплекс
• Параллелотоп
• Распятие (Corpus Hypercubus) (известное произведение искусства)

Примечания

1. Эльте, EL (1912). «IV, Пятимерный полуправильный многогранник». Полуправильные многогранники гиперпространств . Нидерланды: Университет Гронингена . ISBN 141817968X.
2. Coxeter 1973, стр. 122–123, §7.2, см. иллюстрацию Рис. 7.2 C.
3. Коксетер 1973, с. 122, §7·25.
4. Джонсон, Норман В.; Геометрии и преобразования , Издательство Кембриджского университета, 2018, стр.224.
5. Коксетер, HSM (1974), Правильные комплексные многогранники , Лондон и Нью-Йорк: Издательство Кембриджского университета , стр. 180, МР  0370328.

Рекомендации

• Боуэн, JP (апрель 1982 г.). «Гиперкуб». Практические вычисления . 5 (4): 97–99. Архивировано из оригинала 30 июня 2008 г. Проверено 30 июня 2008 г.
• Коксетер, HSM (1973). Правильные многогранники (3-е изд.). §7.2. см. рисунок Рис. 7-2 C : Дувр . стр. 122-123. ISBN 0-486-61480-8.{{cite book}}: CS1 maint: location (link)п. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n измерениях ( n  ≥ 5).
• Хилл, Фредерик Дж.; Джеральд Р. Петерсон (1974). Введение в теорию коммутации и логическое проектирование: второе издание . Нью-Йорк: Джон Уайли и сыновья . ISBN 0-471-39882-9.См. главу 7.1 «Кубическое представление булевых функций», в которой понятие «гиперкуб» вводится как средство демонстрации кода расстояния 1 ( кода Грея ) в качестве вершин гиперкуба, а затем гиперкуб с его вершинами, помеченными таким образом, является сжимается в два измерения, образуя либо диаграмму Вейча , либо карту Карно .

Внешние ссылки

• Вайсштейн, Эрик В. «Гиперкуб». Математический мир .
• Вайсштейн, Эрик В. «Графы гиперкуба». Математический мир .
• Вращение гиперкуба Энрике Зелени, Демонстрационный проект Wolfram .
• Загрузки Hypercube Руди Ракера и Фариде Дормишян
• A001787 Число ребер в n-мерном гиперкубе. в OEIS