Динамичный бильярд

Динамическая система абстрагируется от идеальной игры в бильярд с упругими столкновениями за пределами границ

Частица, движущаяся внутри стадиона Бунимовича, известный хаотический бильярд. Смотрите раздел Программное обеспечение для создания такой анимации.

Динамический бильярд — это динамическая система , в которой частица чередует свободное движение (обычно по прямой) и зеркальные отражения от границы. Когда частица сталкивается с границей, она отражается от нее без потери скорости (т. е. упругие столкновения). Бильярды — это гамильтоновы идеализации игры в бильярд , но где область, ограниченная границей, может иметь форму, отличную от прямоугольной, и даже быть многомерной. Динамические бильярды также можно изучать на неевклидовых геометриях ; действительно, первые исследования бильярдов установили их эргодическое движение на поверхностях постоянной отрицательной кривизны . Изучение бильярдов, которые находятся вне области, а не находятся в области, известно как теория внешнего бильярда .

Движение частицы в бильярде представляет собой прямую линию с постоянной энергией между отражениями от границы ( геодезической, если риманова метрика бильярдного стола не плоская). Все отражения являются зеркальными : угол падения непосредственно перед столкновением равен углу отражения непосредственно после столкновения. Последовательность отражений описывается бильярдной картой , которая полностью характеризует движение частицы.

Бильярды охватывают всю сложность гамильтоновых систем, от интегрируемости до хаотического движения , без трудностей интегрирования уравнений движения для определения его отображения Пуанкаре . Биркгоф показал, что бильярдная система с эллиптическим столом интегрируема.

Уравнения движения

Гамильтониан для частицы массой m, свободно движущейся без трения по поверхности, имеет вид:

${\displaystyle H(p,q)={\frac {p^{2}}{2m}}+V(q)}$

где — потенциал, равный нулю внутри области , в которой может двигаться частица, и бесконечности в противном случае: ${\displaystyle V(q)}$ ${\displaystyle \Omega }$

${\displaystyle V(q)={\begin{cases}0&q\in \Omega \\\infty &q\notin \Omega \end{cases}}}$

Эта форма потенциала гарантирует зеркальное отражение на границе. Кинетический член гарантирует, что частица движется по прямой линии, без изменения энергии. Если частица должна двигаться по неевклидову многообразию , то гамильтониан заменяется на:

${\displaystyle H(p,q)={\frac {1}{2m}}p^{i}p^{j}g_{ij}(q)+V(q)}$

где — метрический тензор в точке . Ввиду очень простой структуры этого гамильтониана уравнения движения частицы, уравнения Гамильтона–Якоби , представляют собой не что иное, как геодезические уравнения на многообразии: частица движется вдоль геодезических . ${\displaystyle g_{ij}(q)}$ ${\displaystyle q\;\in \;\Omega }$

Известные бильярдные классы и бильярдные курсы

Бильярд Адамара

Биллиарды Адамара касаются движения свободной точечной частицы на поверхности постоянной отрицательной кривизны, в частности, простейшей компактной римановой поверхности с отрицательной кривизной, поверхности рода 2 (бублик с двумя дырками). Модель точно решаема и задается геодезическим потоком на поверхности. Это самый ранний пример детерминированного хаоса , когда-либо изученный, введенный Жаком Адамаром в 1898 году.

Бильярд Артина

Биллиард Артина рассматривает свободное движение точечной частицы на поверхности постоянной отрицательной кривизны, в частности, на простейшей некомпактной римановой поверхности , поверхности с одним острием. Она примечательна тем, что точно решаема, и при этом не только эргодична , но и сильно перемешивает . Это пример системы Аносова . Эта система была впервые изучена Эмилем Артином в 1924 году.

Рассеивающие и полурассеивающие бильярды

Пусть M — полное гладкое риманово многообразие без края, максимальная секционная кривизна которого не больше K и с радиусом инъективности . Рассмотрим набор из n геодезически выпуклых подмножеств (стенок) , , таких, что их границы являются гладкими подмногообразиями коразмерности один. Пусть , где обозначает внутренность множества . Множество будем называть бильярдным столом. Рассмотрим теперь частицу, которая движется внутри множества B с единичной скоростью по геодезической, пока не достигнет одного из множеств B _i (такое событие называется столкновением), где она отражается по закону «угол падения равен углу отражения» (если она достигает одного из множеств , , то траектория не определена после этого момента). Такая динамическая система называется полурассеивающим бильярдом . Если стенки строго выпуклые, то бильярд называется рассеивающим . Название мотивировано наблюдением, что локально параллельный пучок траекторий расходится после столкновения со строго выпуклой частью стены, но остается локально параллельным после столкновения с плоским участком стены. ${\displaystyle \rho >0}$ ${\displaystyle B_{i}\subset M}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle B=M\ (\bigcup _{i=1}^{n}\operatorname {Int} (B_{i}))}$ ${\displaystyle \operatorname {Int} (B_{i})}$ ${\displaystyle B_{i}}$ ${\displaystyle B\subset M}$ ${\displaystyle B_{i}\cap B_{j}}$ ${\displaystyle i\neq j}$

Рассеивающая граница играет для бильярдов ту же роль, что и отрицательная кривизна для геодезических потоков, вызывая экспоненциальную неустойчивость динамики. Именно этот рассеивающий механизм придает рассеивающим бильярдам их сильнейшие хаотические свойства, как это установил Яков Г. Синай . [ ^1] А именно, бильярды являются эргодическими , перемешивающими , бернуллиевскими , имеющими положительную энтропию Колмогорова-Синая и экспоненциальный распад корреляций .

Хаотические свойства обычных полурассеивающих бильярдов изучены недостаточно хорошо, однако свойства одного важного типа полурассеивающих бильярдов, твердого шарового газа , изучались довольно подробно с 1975 года (см. следующий раздел).

Общие результаты Дмитрия Бураго и Сержа Ферлегера ^[2] по равномерной оценке числа столкновений в невырожденных полурассеивающих бильярдах позволяют установить конечность их топологической энтропии и не более чем экспоненциальный рост периодических траекторий. ^[3] Напротив, вырожденные полурассеивающие бильярды могут иметь бесконечную топологическую энтропию. ^[4]

Газ Лоренца, он же Синайский бильярд

Частица, движущаяся внутри синайского бильярда, также известного как газ Лоренца.

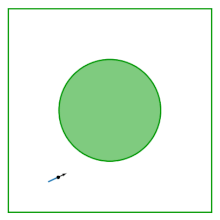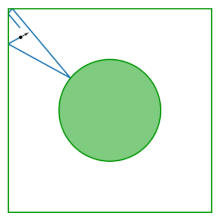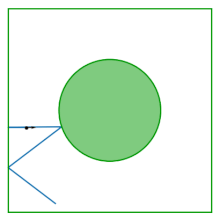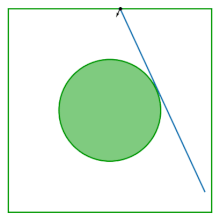
Стол газа Лоренца (также известный как бильярд Синая) представляет собой квадрат с удаленным из его центра диском; стол плоский, не имеющий кривизны. Бильярд возникает из изучения поведения двух взаимодействующих дисков, отскакивающих внутри квадрата, отражающихся от границ квадрата и друг от друга. Исключая центр масс как переменную конфигурации, динамика двух взаимодействующих дисков сводится к динамике в бильярде Синая.

Биллиард был представлен Яковом Григорьевичем Синаем как пример взаимодействующей гамильтоновой системы , которая проявляет физические термодинамические свойства: почти все (до нулевой меры) ее возможные траектории являются эргодическими и она имеет положительный показатель Ляпунова .

Величайшим достижением Синая в этой модели было то, что он показал, что классический ансамбль Больцмана–Гиббса для идеального газа по сути представляет собой максимально хаотичный бильярд Адамара.

Бильярд с прыгающим шаром

Частица подвергается воздействию постоянной силы (например, гравитации Земли) и рассеивается неупруго на периодически гофрированном вибрирующем полу. Когда пол сделан из дуг или окружностей - в определенном интервале частот - можно дать полуаналитические оценки скорости экспоненциального разделения траекторий. ^[5]

Стадион Бунимовича

Стол, называемый стадионом Бунимовича, представляет собой прямоугольник, увенчанный полукругами, фигура, называемая стадионом . До того, как он был представлен Леонидом Бунимовичем , считалось, что бильярды с положительными показателями Ляпунова нуждаются в выпуклых рассеивателях, таких как диск в бильярде Синая, чтобы производить экспоненциальное расхождение орбит. Бунимович показал, что, рассматривая орбиты за пределами фокусной точки вогнутой области, можно получить экспоненциальное расхождение.

Магнитный бильярд

Движение заряженной частицы внутри синайского бильярда с перпендикулярным магнитным полем.

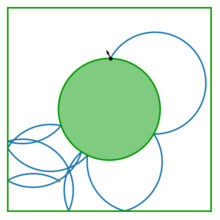
Магнитные бильярды представляют собой бильярды, в которых заряженная частица распространяется в присутствии перпендикулярного магнитного поля. В результате траектория частицы меняется с прямой линии на дугу окружности. Радиус этой окружности обратно пропорционален напряженности магнитного поля. Такие бильярды были полезны в реальных приложениях бильярдов, обычно моделируя наноустройства (см. Приложения).

Обобщенный бильярд

Обобщенные биллиарды (ББ) описывают движение материальной точки (частицы) внутри замкнутой области с кусочно-гладкой границей . На границе скорость точки преобразуется при действии на частицу обобщенного закона биллиарда. ББ были введены Л. Д. Пустыльниковым в общем случае ^[6] и в случае, когда — параллелепипед ^[7] в связи с обоснованием второго начала термодинамики . С физической точки зрения ББ описывают газ, состоящий из конечного числа частиц, движущихся в сосуде, при этом стенки сосуда нагреваются или остывают. Суть обобщения заключается в следующем. При попадании частицы на границу ее скорость преобразуется с помощью заданной функции , определенной на прямом произведении (где — вещественная прямая, — точка границы, — время), по следующему закону. Предположим, что траектория частицы, движущейся со скоростью , пересекается в точке в момент времени . Тогда в момент времени частица приобретает скорость , как если бы она испытала упругий толчок со стороны бесконечно тяжелой плоскости , касательной к в точке , и в момент времени движется по нормали к в со скоростью . Подчеркнем, что положение самой границы фиксировано, а ее воздействие на частицу определяется через функцию . ${\displaystyle \Pi \,\subset \,\mathbb {R} ^{n}}$ ${\displaystyle \Gamma }$ ${\displaystyle \Gamma }$ ${\displaystyle \Pi }$ ${\displaystyle \Gamma }$ ${\displaystyle f(\gamma ,\,t)}$ ${\displaystyle \Gamma \,\times \,\mathbb {R} ^{1}}$ ${\displaystyle \mathbb {R} ^{1}}$ ${\displaystyle \gamma \,\in \,\Gamma }$ ${\displaystyle t\,\in \,\mathbb {R} ^{1}}$ ${\displaystyle v}$ ${\displaystyle \Gamma }$ ${\displaystyle \gamma \,\in \,\Gamma }$ ${\displaystyle t^{*}}$ ${\displaystyle t^{*}}$ ${\displaystyle v^{*}}$ ${\displaystyle \Gamma ^{*}}$ ${\displaystyle \Gamma }$ ${\displaystyle \gamma }$ ${\displaystyle t^{*}}$ ${\displaystyle \Gamma }$ ${\displaystyle \gamma }$ ${\displaystyle \textstyle {\frac {\partial f}{\partial t}}(\gamma ,\,t^{*})}$ ${\displaystyle f}$

Положительное направление движения плоскости мы принимаем внутрь . Таким образом , если производная , то частица ускоряется после удара. ${\displaystyle \Gamma ^{*}}$ ${\displaystyle \Pi }$ ${\displaystyle \textstyle {\frac {\partial f}{\partial t}}(\gamma ,\,t)\;>\;0}$

Если скорость , приобретённая частицей в результате указанного выше закона отражения, направлена ​​внутрь области , то частица покинет границу и продолжит движение до следующего столкновения с . Если скорость направлена ​​наружу от , то частица останется в точке , пока в какой-то момент взаимодействие с границей не заставит частицу покинуть её. ${\displaystyle v^{*}}$ ${\displaystyle \Pi }$ ${\displaystyle \Pi }$ ${\displaystyle \Gamma }$ ${\displaystyle v^{*}}$ ${\displaystyle \Pi }$ ${\displaystyle \Gamma }$ ${\displaystyle \gamma }$ ${\displaystyle {\tilde {t}}\;>\;t^{*}}$

Если функция не зависит от времени , т. е. , то обобщенный биллиард совпадает с классическим. ${\displaystyle f(\gamma ,\,t)}$ ${\displaystyle t}$ ${\displaystyle \textstyle {\frac {\partial f}{\partial t}}\;=\;0}$

Этот обобщенный закон отражения очень естественен. Во-первых, он отражает очевидный факт, что стенки сосуда с газом неподвижны. Во-вторых, воздействие стенки на частицу по-прежнему представляет собой классический упругий толчок. По сути, мы рассматриваем бесконечно мало движущиеся границы с заданными скоростями.

Рассматривается отражение от границы как в рамках классической механики (ньютоновский случай), так и теории относительности (релятивистский случай). ${\displaystyle \Gamma }$

Основные результаты: в ньютоновском случае энергия частицы ограничена, энтропия Гиббса постоянна, ^{[7] [8] [9]} (в примечаниях), а в релятивистском случае энергия частицы, энтропия Гиббса, энтропия относительно фазового объема возрастают до бесконечности, ^{[7] [9]} (в примечаниях), ссылки на обобщенные биллиарды.

Квантовый хаос

Квантовая версия биллиарда легко изучается несколькими способами. Классический гамильтониан для биллиарда, приведенный выше, заменяется стационарным уравнением Шредингера или, точнее, ${\displaystyle H\psi \;=\;E\psi }$

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi _{n}(q)=E_{n}\psi _{n}(q)}$

где — Лапласиан . Потенциал, который бесконечен вне области, но равен нулю внутри нее, переводится в граничные условия Дирихле : ${\displaystyle \nabla ^{2}}$ ${\displaystyle \Omega }$

${\displaystyle \psi _{n}(q)=0\quad {\mbox{for}}\quad q\notin \Omega }$

Как обычно, волновые функции считаются ортонормальными :

${\displaystyle \int _{\Omega }{\overline {\psi _{m}}}(q)\psi _{n}(q)\,dq=\delta _{mn}}$

Любопытно, что уравнение Шредингера для свободного поля такое же, как и уравнение Гельмгольца ,

${\displaystyle \left(\nabla ^{2}+k^{2}\right)\psi =0}$

с

${\displaystyle k^{2}={\frac {1}{\hbar ^{2}}}2mE_{n}}$

Это означает, что двух- и трехмерные квантовые бильярды могут быть смоделированы классическими резонансными модами радиолокационной полости заданной формы, что открывает путь к экспериментальной проверке. (Изучение мод радиолокационной полости должно быть ограничено поперечными магнитными (TM) модами, поскольку именно они подчиняются граничным условиям Дирихле).

Полуклассический предел соответствует , что можно считать эквивалентным , масса увеличивается так, что она ведет себя классически. ${\displaystyle \hbar \;\to \;0}$ ${\displaystyle m\;\to \;\infty }$

В качестве общего утверждения можно сказать, что всякий раз, когда классические уравнения движения интегрируемы ( например, прямоугольные или круглые бильярдные столы), то квантово-механическая версия бильярда полностью разрешима. Когда классическая система хаотична, то квантовая система, как правило, не является точно разрешимой и представляет многочисленные трудности в ее квантовании и оценке. Общее исследование хаотических квантовых систем известно как квантовый хаос .

Особенно яркий пример рубцевания на эллиптическом столе дает наблюдение так называемого квантового миража .

Приложения

Бильярды, как квантовые, так и классические, применялись в нескольких областях физики для моделирования весьма разнообразных систем реального мира. Примерами служат лучевая оптика , ^[10] лазеры , ^{[11] [12]} акустика , ^[13] оптические волокна (например, волокна с двойной оболочкой ^{[14] [15]} ) или квантово-классическое соответствие. ^[16] Одним из наиболее частых их применений является моделирование частиц, движущихся внутри наноустройств, например, квантовых точек , ^{[17] [18]} pn-переходов , ^[19] сверхрешеток антиточек, ^{[20] [21]} и других. Причина такой широко распространенной эффективности бильярдов как физических моделей заключается в том, что в ситуациях с небольшим количеством беспорядка или шума движение, например, частиц, таких как электроны или световые лучи, очень похоже на движение точечных частиц в бильярдах. Кроме того, энергосберегающий характер столкновений частиц является прямым отражением закона сохранения энергии гамильтоновой механики.

Программное обеспечение

Открытое программное обеспечение для моделирования бильярда существует для различных языков программирования. От самого последнего к самому старому, существующее программное обеспечение: DynamicalBilliards.jl (Julia), Bill2D (C++) и Billiard Simulator (Matlab). Анимации, представленные на этой странице, были сделаны с помощью DynamicalBilliards.jl.

Смотрите также

• Модель Ферми–Улама (бильярды с колеблющимися стенками)
• Алгоритм сжатия Любачевского–Стиллингера моделирует столкновения твердых сфер не только с границами, но и между собой, увеличиваясь в размерах ^[15]
• Арифметический бильярд
• Проблема с освещением

Примечания

1. "Архивная копия" (PDF) . Архивировано из оригинала (PDF) 2013-12-31 . Получено 2014-06-06 .{{cite web}}: CS1 maint: архивная копия как заголовок ( ссылка )
2. Бураго, Д.; Ферлегер, С.; Кононенко, А. (1 января 1998 г.). «Равномерные оценки числа столкновений в полурассеивающих бильярдах». Annals of Mathematics . 147 (3): 695–708. doi :10.2307/120962. JSTOR  120962.
3. Бураго, Д.; Ферлегер, С. (26 мая 1997 г.). «Топологическая энтропия полудисперсных биллиардов». Эргодическая теория и динамические системы . 18 (4): 791. doi :10.1017/S0143385798108246. S2CID  122549772.
4. Бураго, Д. (1 февраля 2006 г.). «Полурассеивающие биллиарды бесконечной топологической энтропии». Эргодическая теория и динамические системы . 26 (1): 45–52. doi :10.1017/S0143385704001002. S2CID  121644309.
5. Матьяш, Ласло; Барна, Имре Ференц (2011). «Геометрическое происхождение хаотичности в бильярде с прыгающим шаром». Хаос, солитоны и фракталы . 44 (12): 1111–1116. arXiv : 1003.2505 . дои :10.1016/j.chaos.2011.10.002.
6. Пустыльников, Л. Д. (1999). «Закон возрастания энтропии и обобщенные биллиарды». Математические обзоры . 54 (3): 650–651. Bibcode :1999RuMaS..54..650P. doi :10.1070/rm1999v054n03abeh000168. S2CID  250902640.
7. Пустыльников, Л. Д. (1995). "Модели Пуанкаре, строгое обоснование второго закона термодинамики из механики и механизм ускорения Ферми". Математические обзоры . 50 (1): 145–189. Bibcode :1995RuMaS..50..145P. doi :10.1070/rm1995v050n01abeh001663. S2CID  250875392.
8. Пустыльников, Л. Д. (2005). «Обобщенные ньютоновские периодические биллиарды в шаре». Математические обзоры . 60 (2): 365–366. Bibcode :2005RuMaS..60..365P. doi :10.1070/RM2005v060n02ABEH000839. S2CID  250856558.
9. Дерябин, Михаил В.; Пустыльников, Лев Д. (2007). "Неравновесный газ и обобщенные бильярды". Журнал статистической физики . 126 (1): 117–132. Bibcode :2007JSP...126..117D. doi :10.1007/s10955-006-9250-4. S2CID  55957240.
10. Кузнецов, Дмитрий; Молони, Джером В. (сентябрь 2004 г.). «Граничное поведение мод лапласиана Дирихле». Журнал современной оптики . 51 (13): 1955–1962. Bibcode : 2004JMOp...51.1955K. doi : 10.1080/09500340408232504. ISSN  0950-0340. S2CID  30880255.
11. Стоун, А. Дуглас (июнь 2010 г.). «Хаотические бильярдные лазеры». Nature . 465 (7299): 696–697. doi : 10.1038/465696a . ISSN  1476-4687. PMID  20535191.
12. Gmachl, C. (1998-06-05). "Мощное направленное излучение микролазеров с хаотическими резонаторами". Science . 280 (5369): 1556–1564. arXiv : cond-mat/9806183 . Bibcode :1998Sci...280.1556G. doi :10.1126/science.280.5369.1556. PMID  9616111. S2CID  502055.
13. Коянаги, Синъитиро; Накано, Такеру; Кавабе, Тетсуджи (2008-08-01). «Применение гамильтониана движения лучей к акустике помещений». Журнал Акустического общества Америки . 124 (2): 719–722. Bibcode : 2008ASAJ..124..719K. doi : 10.1121/1.2946714. ISSN  0001-4966. PMID  18681564.
14. Leproux, P.; S. Fevrier; V. Doya; P. Roy; D. Pagnoux (2003). «Моделирование и оптимизация двухоболочечных волоконных усилителей с использованием хаотического распространения накачки». Optical Fiber Technology . 7 (4): 324–339. Bibcode : 2001OptFT...7..324L. doi : 10.1006/ofte.2001.0361.
15. Б. Д. Любачевский и Ф. Х. Стиллингер, Геометрические свойства случайных дисковых упаковок, J. Statistical Physics 60 (1990), 561-583 http://www.princeton.edu/~fhs/geodisk/geodisk.pdf
16. Штокманн, Х.-Й.; Штейн, Й. (1990-05-07). " Квантовый хаос в бильярдах, изученный с помощью поглощения микроволн". Physical Review Letters . 64 (19): 2215–2218. Bibcode : 1990PhRvL..64.2215S. doi : 10.1103/PhysRevLett.64.2215. ISSN  0031-9007. PMID  10041617.
17. Пономаренко, LA; Шедин, F.; Кацнельсон, MI; Янг, R.; Хилл, EW; Новоселов, KS; Гейм, AK (2008-04-18). "Хаотический бильярд Дирака в квантовых точках графена". Science . 320 (5874): 356–358. arXiv : 0801.0160 . Bibcode :2008Sci...320..356P. doi :10.1126/science.1154663. ISSN  0036-8075. PMID  18420930. S2CID  206511356.
18. Bird, Jonathan P., ред. (2003). Электронный транспорт в квантовых точках . doi :10.1007/978-1-4615-0437-5. ISBN 978-1-4020-7459-2.
19. Чэнь, Шаовэнь; Хань, Чжэн; Элахи, Мирза М.; Хабиб, К. М. Масум; Ван, Лэй; Вэнь, Бо; Гао, Юанда; Танигучи, Такаши; Ватанабэ, Кэндзи; Хон, Джеймс; Гош, Авик В. (30.09.2016). «Электронная оптика с pn-переходами в баллистическом графене». Science . 353 (6307): 1522–1525. arXiv : 1602.08182 . Bibcode :2016Sci...353.1522C. doi :10.1126/science.aaf5481. ISSN  0036-8075. PMID  27708099. S2CID  118443999.
20. Weiss, D.; Roukes, ML; Menschig, A.; Grambow, P.; von Klitzing, K.; Weimann, G. (1991-05-27). "Электронный пинбол и соизмеримые орбиты в периодическом массиве рассеивателей" (PDF) . Physical Review Letters . 66 (21): 2790–2793. Bibcode :1991PhRvL..66.2790W. doi :10.1103/PhysRevLett.66.2790. ISSN  0031-9007. PMID  10043617.
21. Дацерис, Джордж; Гейзель, Тео; Флейшманн, Рагнар (2019-04-30). «Надежность баллистического транспорта в сверхрешетках антиточек». New Journal of Physics . 21 (4): 043051. arXiv : 1711.05833 . Bibcode : 2019NJPh...21d3051D. doi : 10.1088/1367-2630/ab19cc . ISSN  1367-2630.

Ссылки

Бильярд Синая

• Синай, Я. Г. (1963). "[К основам эргодической гипотезы для динамической системы статистической механики]". Доклады Академии наук СССР . 153 (6): 1261–1264.(на английском языке, Докл. сов. мат. 4 (1963) стр. 1818–1822).
• Я. Г. Синай, «Динамические системы с упругими отражениями», Успехи математических наук , 25 (1970) стр. 137–191.
• В. И. Арнольд и А. Авез, Эргодическая теория динамических систем (1967), Готье-Виллар, Париж. (Английское издание: Бенджамин-Каммингс, Ридинг, Массачусетс, 1968 г.). (Содержит обсуждение и ссылки на бильярд Синая.)
• D. Heitmann, JP Kotthaus, «Спектроскопия массивов квантовых точек», Physics Today (1993) стр. 56–63. (Обзор экспериментальных испытаний квантовых версий бильярдов Синая, реализованных в виде наномасштабных (мезоскопических) структур на кремниевых пластинах.)
• С. Шридхар и В. Т. Лу, «Синайские бильярды, дзета-функции Рюэля и резонансы Рюэля: микроволновые эксперименты», (2002) Журнал статистической физики , т. 108 , №№ 5/6, стр. 755–766.
• Линас Вепстас, «Бильярды Синая» , (2001). (Предоставляет изображения биллиардов Синая в трехмерном пространстве, полученные с помощью трассировки лучей. Эти изображения наглядно демонстрируют сильную эргодичность системы.)
• Н. Чернов и Р. Маркарян, «Хаотические бильярды», 2006, Математический обзор и монографии № 127, АМН.

Странные бильярды

• T. Schürmann и I. Hoffmann, Энтропия странных биллиардов внутри n-симплексов. J. Phys. A28, стр. 5033ff, 1995. PDF-документ

Стадион Бунимовича

• Л.А.Бунимович (1979). «Об эргодических свойствах нигде не рассеивающихся биллиардов». Commun Math Phys . 65 (3): 295–312. Bibcode : 1979CMaPh..65..295B. doi : 10.1007/BF01197884. S2CID  120456503.
• Л. А. Бунимович и Я. Г. Синай (1980). «Марковские разбиения для рассеянных биллиардов». Commun Math Phys . 78 (2): 247–280. Bibcode : 1980CMaPh..78..247B. doi : 10.1007/bf01942372. S2CID  123383548.
• Флэш-анимация, иллюстрирующая хаотичный стадион имени Бунимовича

Обобщенный бильярд

• М. В. Дерябин и Л. Д. Пустыльников, «Обобщенные релятивистские бильярды», Reg. and Chaotic Dyn. 8(3), стр. 283–296 (2003).
• М. В. Дерябин и Л. Д. Пустыльников, «Об обобщенных релятивистских бильярдах во внешних силовых полях», Письма в журнал математической физики , 63(3), стр. 195–207 (2003).
• М. В. Дерябин и Л. Д. Пустыльников, «Экспоненциальные аттракторы в обобщенных релятивистских бильярдах», Comm. Math. Phys. 248(3), стр. 527–552 (2004).

Внешние ссылки

• Вайсштейн, Эрик В. «Бильярд». Математический мир .
• Статья в Scholarpedia о Динамических бильярдах (Леонид Бунимович)
• Введение в динамические системы с использованием бильярда, Институт физики сложных систем Общества Макса Планка